數據驅動的服裝物流分類及訂貨策略研究*

□ 袁 媛，高 波

(太原科技大學 交通與物流學院，山西 太原 030024)

更好、更有效、更經濟地進行庫存管理是解決服裝企業問題的最佳方法，但許多服裝專賣店的庫存管理只是依據經驗進行，缺乏一定的科學性，因而需要改進。

西方學術界對庫存管理的研究起步較早，研究范圍涉及的領域寬泛。Taleizadeh等[1]將EOQ模型和預付購買模型進行結合，構建了兩者的聯合模型，用遺傳算法對聯合模型進行了優化。Gour Chandra Mahata、Sujit Kumar De[2]建立了零售商向信用風險客戶出售劣質商品的最優批量策略，使零售商在周期內單位時間的總利潤與最優采購量的關系最大化。Makoena Sebatjane及Olufemi Adetunji[3]通過建立描述手頭問題的成本最小化的庫存模型來改善庫存管理，實現食品生產鏈中相當大的成本節約。

隨著計算機輔助的庫存管理階段的到來，國內學者在庫存管理方面的研究數量和成果也極為可觀。江玉杰等[4]提出需求非正態分布下服裝產品安全庫存決策算法，然后通過具體算例驗證該算法的可行性和有效性。研究結果表明，在服裝產品生命周期內,提高成熟期內的安全庫存和降低衰退期的安全庫存,可以減少服裝經銷商不必要的安全庫存；陳啟等[5]研究需求依賴于價格和時尚程度的服裝庫存模型，考慮體驗服務投資可提高服裝時尚度、促銷降價可改善銷售需求的作用，構建一般情形、體驗服務投資情形、促銷努力情形以及服務與促銷聯合4種情形下的優化訂貨和定價模型，分析體驗服務投資和促銷努力聯合時對服裝零售商優化決策的影響。

基于上述國內外研究成果，可以看出庫存倉儲成本對于服裝企業成本有著重大的影響。對于需要提供良好服務的服裝業而言，擁有完善的庫存管理理念、先進的庫存管理技術是很重要的。

1 問題描述

通過對美邦進行六力分析和SWOT分析發現，美邦存在嚴重的庫存問題，需要進一步對其服裝訂貨策略進行研究。根據駱楊[6]分析“快時尚”的服裝行業的庫存控制問題，應當先以庫存問題為切入點，分析庫存問題產生的原因和服裝的需求特點。其次，應采用不同的分類方法，對服裝的類別進行分類，分類方法不同，產生的類別也不同。最后，基于服裝的分類以及歷史銷售數據，來預測未來短期服裝的需求量。

因此，本文以美邦服裝作為研究對象，首先通過數據調研，分析美邦存在的高庫存問題；然后使用八爪魚軟件，對天貓美邦專賣店的服裝數據進行收集和整理；其次利用多重與多標準ABC分類法進行分類；同時采用數據挖掘等相關技術，建立系統預測模型，并通過MATLAB進行模型計算；最后對不同分類標準的服裝進行需求預測和訂貨策略研究。

本文的組織結構圖如圖1所示。

圖1 組織結構圖

2 美邦服飾的多重與多標準ABC分類

傳統的服裝產品分類主要是按照ABC分類方法，結合產品的生命周期將服裝分為3類，如表1所示。

表1 傳統服裝業的服裝產品分類

通過表1可知，傳統的服裝產品分類方法較簡單，但是服裝市場已經從原有的批量生產、款式單一發展成種類多、個性化生產[7]。以往服裝業的分類方法已經難以滿足當今服裝市場的需求，因此，在服裝業的庫存管理過程中，應對服裝進行更加細致的劃分。

多重與多標準ABC分類方法主要包括多重和多標準兩個大的層次[8]。多重ABC分析主要是先進行大類分析，再重點對A、B兩類產品進行二重分析，對于C類產品不再進行劃分[9]。多標準ABC分類方法主要利用銷售量、銷售額、利潤、庫存量等標準進行分類。

根據調研內容進行分析，發現數據中春裝和夏裝的銷售價格普遍低于300元(見表2)，按照銷售量、銷售額進行ABC分類，分類的依據為：

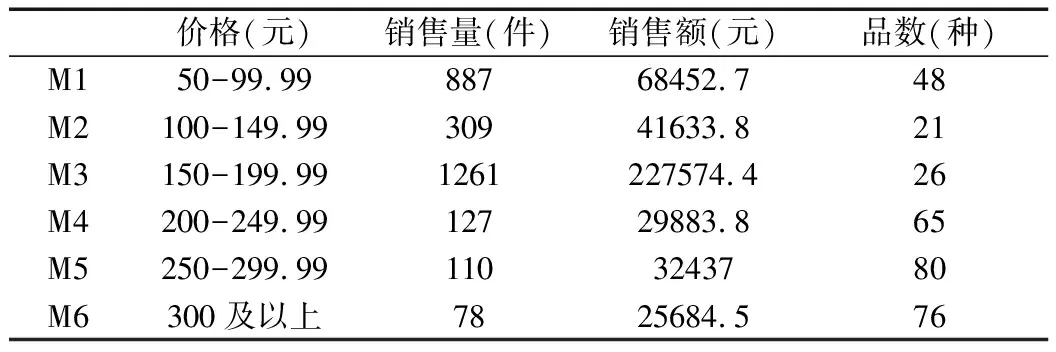
表2 銷售量與銷售額

A類：銷售量/銷售額為45%-75%的，累計品種數目為5%-25%；

B類：銷售量/銷售額為10%-40%的，累計品種數目為15%-45%；

C類：銷售量/銷售額低于10%的，累計品種數目為45%以上。

依據價格標準分的大類，分別進行銷售量和銷售額的單標準分類，分類結果如表3、表4所示。

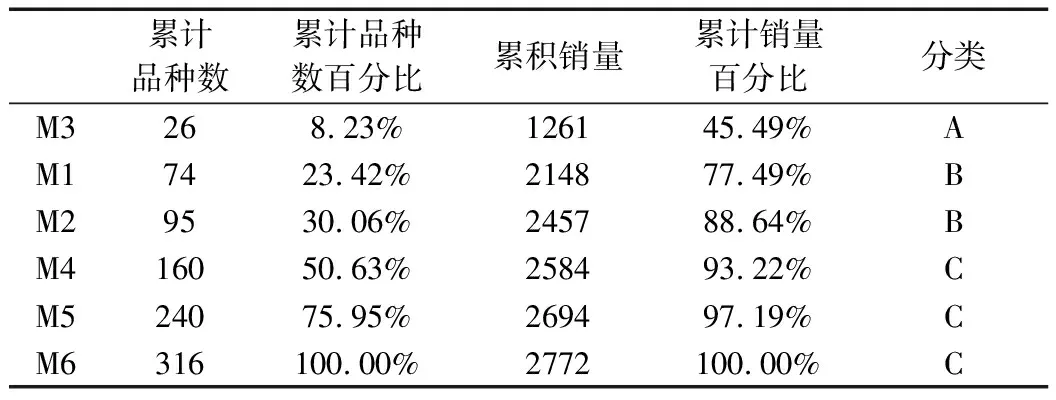
表3 銷售量的單標準分類

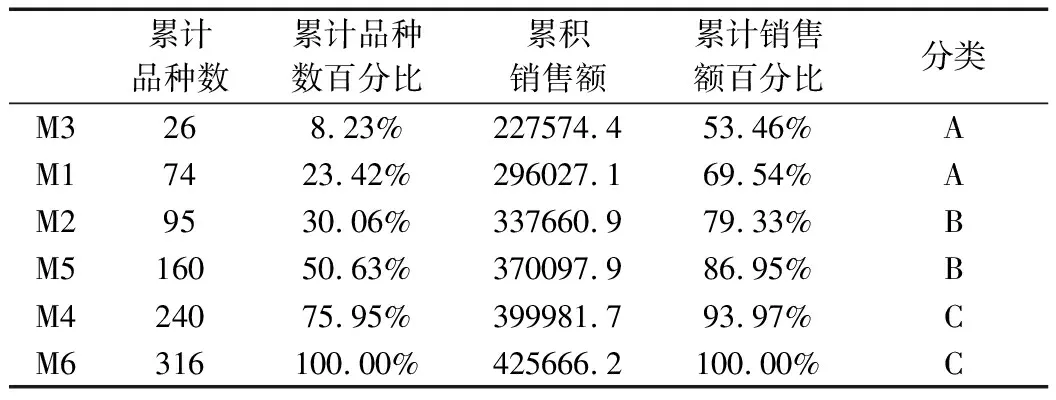
表4 銷售額的單標準分類

通過分析，得出多標準ABC分類的結果為M3,M1,M2,M5,M4,M6，如表5所示。因此，對于M3應進行更精確的訂貨策略分析，嚴格控制其庫存；對于M1和M2應當做到適度控制，適度地減少庫存量；對于含有C類的M4、M5和M6，可采用一般的訂貨管理或根據經驗進行預測。本文針對重點管理的M3進行了進一步的分析。

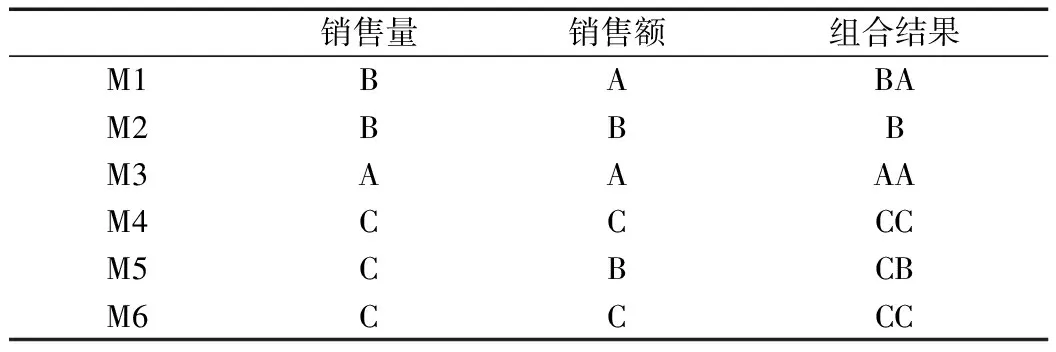
表5 雙標準分類

3 基于雙標準ABC分類的M3多標準分類

對于M3進行同理的雙標準分類，得到的管理順序為牛仔褲、休閑褲、衛衣、襯衫、裙子、外套、毛衣，如表6、表7所示。

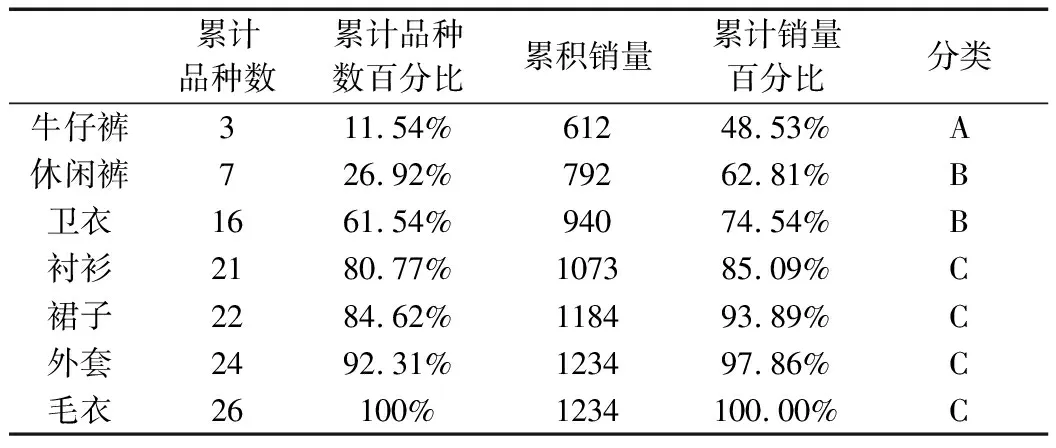
表6 M3的銷售量單標準分類

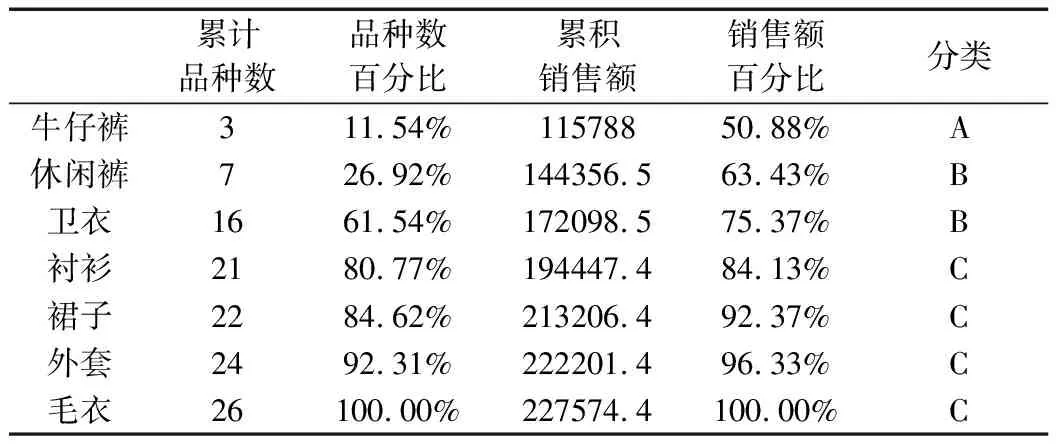
表7 M3的銷售額單標準分類

由分類結果可知，應該進行重點管理的是價格適中的牛仔褲。為提高短期預測的精確性，本文采用灰色預測模型進行預測。

4 基于灰色預測的高銷量服飾訂貨策略

4.1 灰色預測模型

灰色預測模型中最常用的是GM(1,1)模型，指的是運用一階微分方程，對1個變量，利用離散數據建立微分方程的動態模型。

①灰色預測模型的基本公式如式(1)所示。

(1)

式中，x(0)是模型的灰導數；a是模型的發展系數，u是模型的灰色作用量。

②灰色預測模型的矩陣算式如式(2)-(4)所示。

(2)

Y=[x(0)(2),x(0)(3),x(0)(4),…,x(0)(n)]T

(3)

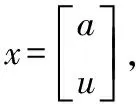
(4)

由式(4)計算出a和u，并得到灰色系統模型的時間響應函數，如式(5)所示。

本組患者50例中，3例因出現并發癥或是由于患者本身因素而死亡，其余均順利在術后7～125天時間內順利拔管，成功轉入康復病房進行康復治療或者治愈之后順利出院。

(5)

由公式(5)進行計算，可得到實際數據的模擬序列函數，如式(6)所示。

(6)

公式(6)可以準確地反映原始數列的變化趨勢、增長(減少)趨勢。當k取1,2,…時，可以求出數據的訓練值，當k大于等于n時，可以求得數據的預測值。

③灰色預測模型結果檢驗，如式(7)-(11)所示。

e為殘差檢驗，A為實際值，G為預測值

e=A-G

(7)

相對殘差

q=E(0)(K)/x(0)(K)=e/A

(8)

S1代表均值

(9)

S2代表殘差均值

(10)

c代表方差比

(11)

4.2 建模分析

本文調研了一款衛衣在上市的8周內每周的總銷量，如表8所示。

表8 衛衣8周內的銷量

利用MATLAB進行數據分析，預測結果如圖2所示。

圖2 灰色預測模型的預測結果

概率P為

(12)

灰色預測公式為

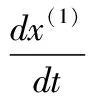
(13)

通過以上的分析，得出灰色預測模型的數據分析結果，如表9所示。發現在概率P=1的情況下，方差比c=0.044846，證明了預測結果優秀。

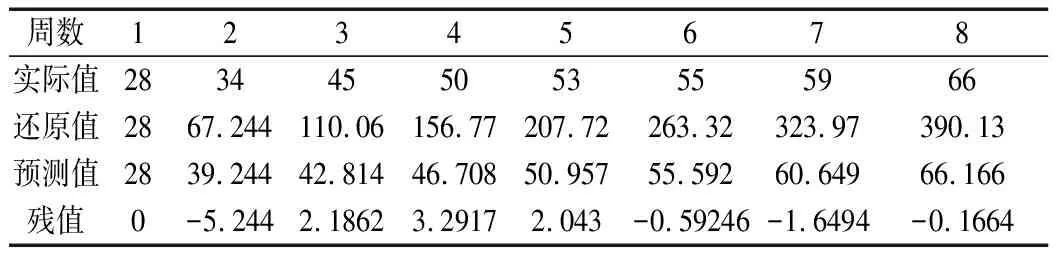
表9 灰色預測模型數據分析

5 結論

本文是以存在高庫存問題的美邦的銷售數據為依托，運用多重與多標準ABC分類法，將服裝數據進行了更加合理的分類。隨后針對重點管理類別中的衛衣銷售數據，建立了灰色預測模型，然后利用MATLAB進行求解，對特定時間段的數據進行了預測，獲得實際值、預測值、誤差等信息。最后，通過概率與誤差的關系進行檢驗。由此，為服裝進貨數量的確定、庫存管理、服務水平等管理決策提供參考價值，以期提高服裝企業發展核心的競爭力以及客戶的服務質量與水平。