巧解繩牽連系統的運動問題

方照明 張文理

(南京師范大學附屬中學，江蘇 南京 210003)

繩牽連系統的運動問題是高中物理中的一類典型問題，主要涉及通過輕繩連接的多個物體的運動學和動力學規律。繩牽連系統的運動問題的難點在于涉及多個物體的運動和受力情況，需先假設物體的速度大小和方向，將速度沿繩和垂直于繩的方向進行分解，對物體運用動量定理，結合沿繩方向速度相等的約束條件，列出多個方程，涉及的未知數較多，求解過程復雜，對學生的思維縝密性和數學運算能力要求較高。本文介紹繩牽連系統運動問題的一種簡單分析方法，解決問題時圍繞“沿繩方向速度相等”這一條件展開，涉及的方程數明顯減少，過程更加簡潔，方法的普適性和拓展性較強。學生掌握了分析問題的關鍵，為研究更為復雜的問題提供了參考。

1 單牽連基礎模型分析

通過輕繩相連的兩個物體組成系統，給其中某一物體一個瞬時沖量，研究另一物體的運動情況。

例1：如圖1所示，兩個質量均為m的小球，用已拉緊的不可伸長的輕繩互相連接，放在光滑的水平桌面上，若突然給小球1一個水平的瞬時沖量I，沖量I與小球1、2連線的夾角為α=60°，求小球2開始運動時的速度。

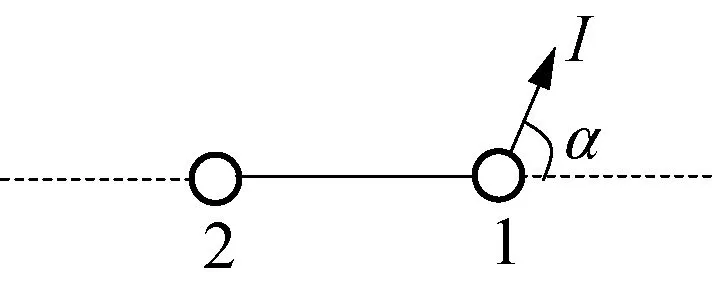
圖1

1.1 常規思路

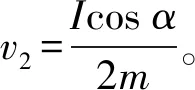
1.2 巧解思路

2 多物體開放式繩牽連問題

通過輕繩依次相連的3個或3個以上的物體組成系統，首尾兩物體不閉合，給其中某物體一個瞬時沖量，研究其他物體的運動情況。

例2：如圖2所示，4個質量均為m的小球，用已拉緊的不可伸長的輕繩互相連接，放在光滑的水平桌面上，α=60°，若給小球1一個沿著小球2、1 連線方向的沖量I，求小球4剛開始運動時的速度。

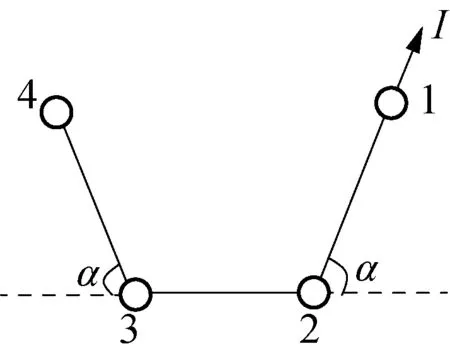
圖2

2.1 常規思路

如圖3所示，設小球1和2間、小球2和3間、小球3和4間的輕繩產生的沖量大小分別為I1、I2和I3，球1、2、3和4的瞬時速度分別為v1、v2、v3和v4，其中v2與小球1和2連線的夾角為β、v3與小球2和3連線的夾角為γ。根據動量定理，對于球1有：I-I1=mv1；對于球2有：I1-I2cosα=mv2cosβ，I2sinα=mv2sinβ；對于球3有：I2-I3cosα=mv3cosγ，I3sinα=mv3sinγ；對于球4有：I3=mv4。根據沿繩方向速度相等的約束條件，沿小球1、2連線方向上有：v1=v2cosβ，沿小球2、3連線方向上有：v2cos (β+α)=v3cosγ，沿小球3、4連線方向上有：v3cos (γ+α)=v4。

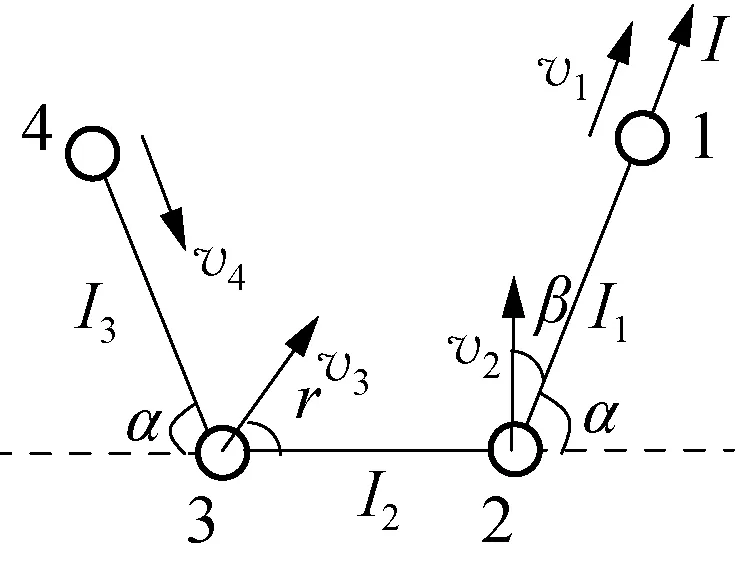
圖3

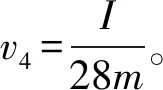
分析：(1) 4個小球剛開始運動時，繩子恰好被拉直，繩子的位置不變；(2) 小球1受到的力產生兩個共線的沖量，小球4受到的力產生一個沖量，兩者速度方向沿繩方向。小球2、3受到的力產生兩個不共線的沖量，可對小球2、3分方向運用動量定理；(3) 由于3段輕繩不可伸長，小球沿繩方向速度相等，可得到三個約束關系。[1]

2.2 巧解思路

為簡化上述分析過程 ，我們嘗試運用“沿繩方向速度相等”這一條件展開分析，具體如下。

圖4

分析：(1) 在以上求解中沒有分析4個小球的實際速度，利用動量定理，直接寫出小球沿繩方向的分速度表達式；(2) 由于3段繩不可伸長，每段繩兩端小球沿該繩的分速度大小相等。通過以上處理，所列方程中涉及的未知量數量大為減少，計算簡便。

3 多物體閉合式繩牽連問題

通過輕繩依次相連的3個或3個以上的物體組成系統，首尾閉合，給其中某物體一個瞬時沖量，研究其他物體的運動情況。

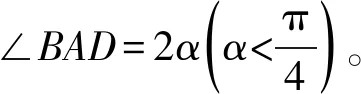
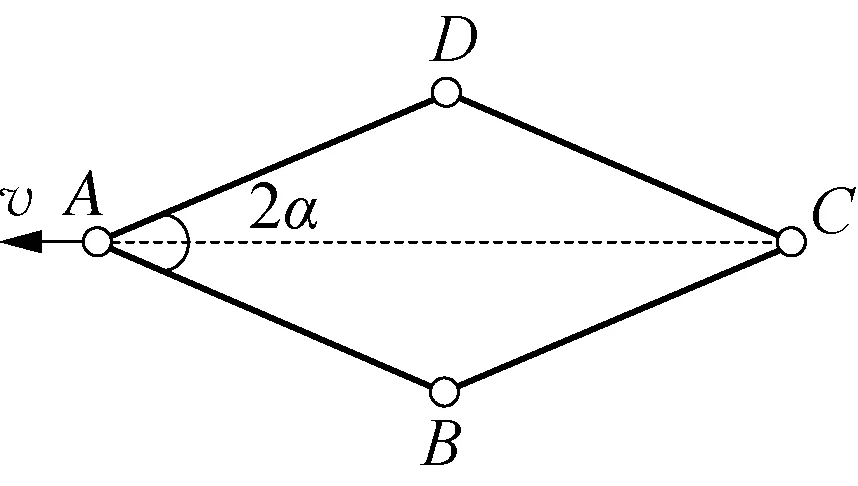
圖5

3.1 常規思路

如圖6所示，設AD和DC繩中力產生的沖量大小分別為I1和I2，D和C質點的瞬時速度分別為vD和vC，其中vD可正交分解為vD1和vD2。 根據動量定理，對于質點C有：2I2cosα=mvC；對于質點D有：I1cosα-I2cosα=mvD1，I1sinα+I2sinα=mvD2。

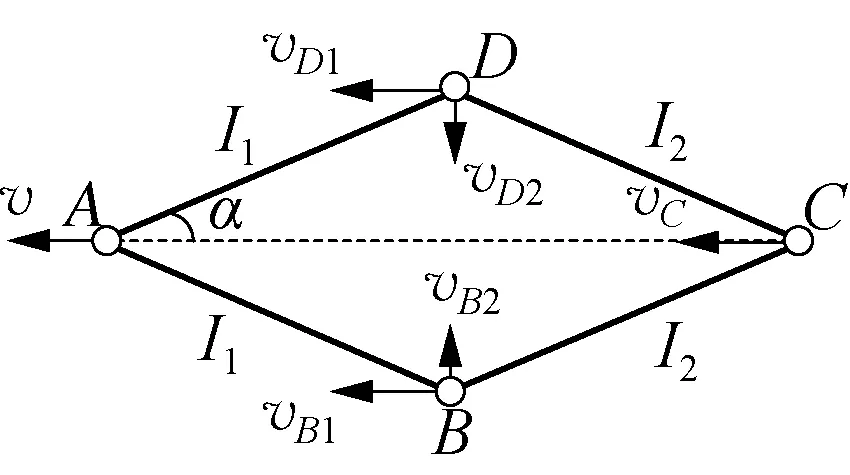
圖6

根據沿繩方向速度相等的約束條件，沿AD繩方向上有：vcosα=vD1cosα+vD2sinα；沿DC繩方向上有：vCcosα=vD1cosα-vD2sinα。

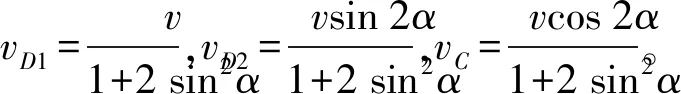
分析：(1) 根據對稱性，質點B和D的速度大小相同，即有vD1=vB1和vD2=vB2，繩AD和AB中力產生的沖量都為I1，繩DC和BC中力產生的沖量都為I2；(2) 對4個質點分方向運用動量定理，由于AD和DC兩段繩不可伸長，質點沿兩繩方向的速度分量相同，可找到兩個約束關系。

3.2 巧解思路

為簡化上述分析過程，筆者嘗試抓住“沿繩方向速度相等”這一條件展開分析。

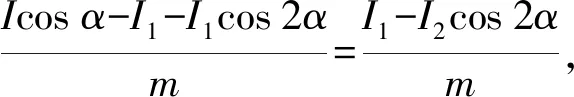
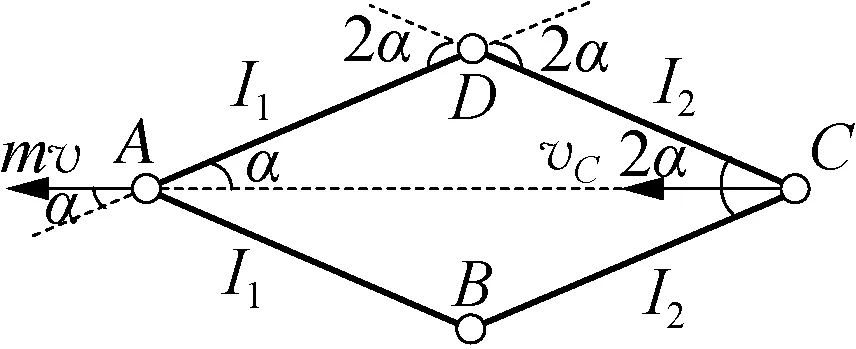
圖7

分析：(1) 根據對稱性，繩AD和AB中力產生的沖量都為I1，繩DC和BC中力產生的沖量都為I2，質點D、B的運動情況一樣，可以只分析3個質點；(2) 根據動量定理，可寫出3個質點沿繩方向分速度的方程；(3) 由于繩不可伸長，每段繩兩端的質點沿繩方向上的分速度相等。[2]通過以上處理，所列方程中涉及的未知量數量大為減少，計算簡便。

4 結語

在平時的教學中，對于同一類問題采用不同的解決思路，有利于拓寬學生的思維和視野，幫助學生抓住問題情境的本質。對于繩牽連系統的運動問題的研究，筆者通過圍繞“沿繩方向速度相等”這一條件展開，極大簡化了問題解決的步驟，降低了運算量，在實際教學中，筆者發現學生對“沿繩方向速度相等”的分析思路更容易理解，且能很快地運用這種方法解決更復雜的問題。