基于積累周期分段編碼的汽車車窗防夾學習算法

馮富霞，李森貴

(1.安徽工程大學 計算機與信息學院，安徽 蕪湖 241000；2.蕪湖莫森泰克汽車科技有限公司 研發部，安徽 蕪湖 241000)

在金融、醫學、監控等領域時間序列數據十分常見，精確并實時地判斷出序列流中的異常非常必要。異常判斷常用方法有數學分布、動態時間回歸、概率后綴樹、預測對比[1]、強力搜索[2]等，理論依據主要有概率統計、鄰近度、判斷模型、回歸模型[3-4]、神經網絡、支持向量機等。統計方法必須符合一定的數學分布；鄰近度法常使用距離或角度差判斷，編碼選擇的不同、差異對比技術選擇的不同對結果的影響較大；判斷模型、神經網絡、支持向量機需要大量內存和運算量；回歸模型參數復雜且參數敏感。

目前計算設備的硬件配置飛速提高，加之云技術的廣泛應用，如果異常判斷基于以上的先進設備及技術，則不用考慮計算量、數據量。但在有些場景下硬件配置是受限制的，甚至配置很低，無法使用高復雜度的算法，如霧計算在某些場景下甚至只有霧滴孤軍奮戰。實時有效地判斷序列流異常的需求不會因場景不同而降低，例如汽車車窗防夾判斷，硬件配置極大受限，對防夾算法的運算量、存儲量要求非常敏感，同時準確度、實時性要求卻十分高，這促使工程人員不斷優化算法。

目前防夾算法有回歸擬合跟隨法，文獻[5]先利用逆伽馬函數擬合，再利用殘差的正態分布檢測異常，適用于殘差符合正態分布的場景。文獻[6-7]使用轉矩線性擬合得到殘差使用閾值判斷。文獻[8]利用高斯濾波濾除部分噪聲，采用類似積分法對脈寬曲線進行計算，將積分面積與閾值比較判斷，對脈沖的始末定位，周期變化敏感。以上都基于模擬系統信號，文獻[5]需要殘差符合正態分布，文獻[6-8]均利用信號計算車窗的機械受力，計算復雜量大，且防夾閾值確定只有文獻[7]給出了復雜推算方法。

利用數據分析和機器學習的技術，通過對大量實采數據的分析，依據數據蘊含的規律設計了簡單、可靠的防夾算法。前期通過對不同路況和時速下的25組數據進行分析，每組3 000～5 000左右數據量，提出了跟隨周期均值顯著化序列異常數據的學習算法，詳見文獻[9]，但是后期發現判斷出的防夾點混雜著少數因路況極度顛簸出現的誤防夾點。文獻[10-11]利用多種算法的融合實現序列數據的預測和異常檢測等，其中包括了分類算法和其有效性的證實，據此,本問題的研究引入了分類算法，并且數據追加到50組深入研究，提出了改進算法。基于積累周期分段編碼的汽車車窗防夾學習算法，實現了簡單、有效、實時地過濾信號流中的誤防夾點。

1 關鍵技術選擇與技術局限性問題的解決

時序序列編碼被廣泛應用的主要有離散傅里葉變換(Discrete Fourier Transform,DFT)、奇異值分解(Singular Value Decomposition,SVD)、分段線性估計(Piecewise Linear,PLA)、符號編碼。DFT基本思想是把序列看成離散量，將其分解為正弦和余弦函數的線性融合函數，從時域變換為頻域空間，對序列的平穩性要求比較高；SVD通過求矩陣的特征矩陣實現序列的降維編碼，著眼全局數據，空間與時間復雜度最高；PLA最簡單，使用廣泛，通過分段線性表示簡約總序列，既保持了宏觀趨勢特征，又適當保留了局部細節，權衡主要由分段的長短決定，適用閔可夫斯基距離度量子序列的相似度，文獻[12]證實PLA的分段聚合近似(Piecewise Aggregate Approximation,PAA)方式比DFT效率高出1～2個數量級；符號法通過離散序列的值域空間實現序列的簡約編碼，對于獲取序列的宏觀趨勢規律最合適，但是局部細節信息喪失太多，如布爾編碼。由于這里需要準確、精確、實時地對序列流進行區分，簡單有效的需求下選取PAA編碼為依據。

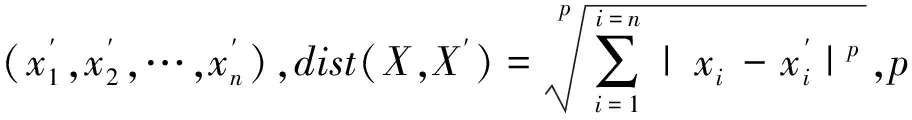
(1)幅平移與幅伸縮問題。序列的慣性決定后續子序列起始點取值的差異以及形成的幅平移，而閔可夫斯基距離法對幅平移和幅伸縮敏感。這里采用子序列的均值差值、分段斜率編碼法，只保留與幅值無關的變化率，成功去掉了幅平移對結果的影響。兩組幅平移子序列如圖1所示。由圖1可知，兩組幅平移子序列，它們的形狀完全相同，如果用幅值編碼序列的方式進行距離對比，兩者顯然不同，而用擬合直線的斜率編碼，它們的斜率相同，進行距離對比結果正好相同。周期分段子序列斜率編碼如圖2所示。由圖2可知，編碼(1.5,0.633,0.52)可去幅平移，編碼與序列的起始點無關，子序列均值差值編碼同理可以去除幅平移對結果的影響。幅伸縮正好是這里比較的依據，需要保留。

圖1 兩組幅平移子序列 圖2 周期分段子序列斜率編碼

此時距離計算與時間維度無關，即為閔可夫斯基距離公式。

2 汽車車窗序列數據特征分析與跟隨周期分段編碼

2.1 汽車車窗序列數據特征分析

這里的汽車車窗防夾序列數據包含霍爾信號和電壓信號，先將兩類數據融合成一組數據，實現數據平滑處理。序列數據正常情況下沿某一均值上下震蕩，會出現均值上下浮動現象，震蕩周期不均勻；防夾子序列數據幅值明顯高于正常數據，屬于連續小幅波動爬升過程；防夾點出現的判斷是障礙物受力超出100 N，因此,實際中防夾子序列只能取到初始爬升區域，不允許放任到最高值的出現。對比周期子序列的數據變化趨勢特征發現，信號序列存在3類變化趨勢模式：緩爬升震蕩式、遞增爬升式、大幅爬升震蕩式，3種模式恰好代表正常情況、防夾情況、劇烈顛簸情況,具體如圖3所示。防夾子序列如果不加干預采集出的后續序列會繼續增大幅度爬升。因此防夾檢測即為分類問題，關鍵是找到分類依據和分類劃分標準，同時在全局序列中抓取正常情況、防夾情況、劇烈顛簸情況的子序列。

圖3 序列的3種分類

通過以上分析可知，序列數據具有慣性，相似序列幅度變化因素使防夾點的閾值無法固定，所以去除慣性因素是算法的關鍵，劃分顯著是算法高準確度的保障。前期根據跟隨周期均值差值算法有效去除慣性因素，依據幅度增長積累可有效地劃分出正常序列，但是防夾序列與劇烈顛簸序列間存在重疊無法區分，需要利用新分類依據和劃分標準進一步完善算法，通過以上特征分析決定利用幅度增長率為分類依據探索再次分類特征。

2.2 利用幅度增長率實現異常序列的分段編碼

要在前期算法的基礎上，實現劇烈顛簸和防夾情況的有效區分。由于原始子序列對應的向量維數眾多(大約40～60維)，維數與最佳跟隨周期的取值有關，數據取值范圍大約在3 000～7 000，為了減小子序列距離計算的復雜度，需要進行重新壓縮編碼，恰當的分割長度下，斜率編碼即可反應序列的宏觀形態，同時又保證子序列間的局部差異特征。

為了提取帶檢測子序列的幅度變化特征，斜率編碼的斜率計算需要對跟隨周期T進行再次合理劃分。在波浪式變化下，3維斜率向量恰好可以反應其形態特征。為了保障算法和跟隨周期起始點的選取不敏感，向后追加了1維同等份斜率，這要求跟隨周期寬度取值要合理，以免出現防夾子序列超出防夾力閾值的限制，前面防夾子序列的特征給出理由，這時即使判斷出防夾，也屬無效，或適當減少追加的數據量。命名此序列編碼方式為4維編碼S(k1,k2,k3,k4)。

斜率計算的改進。線性變化率可以用經典的最小二乘法計算，如式(1)所示:

(1)

式中，α即為k，累計求和，累計次數范圍為1～T。斜率編碼的目的是刻畫變化趨勢特征，不要求百分百的精確，這里把跟隨周期T數據進行3等分分段后，每分段數據元組對數量較少，每分段可再二等分分段，每小段求均值，利用二分段的中點計算斜率改進式(1)。

設S((x1,y1),(x2,y2),…，(xT,yT)),則每分段的斜率

(2)

對比前面公式，運算量以及存儲量明顯降低，在這里效果等同。隨機取一組T/3數據如表1所示。最小二乘法計算k為5.3，改進公式計算為5.5，例如，隨機取T長度子序列編碼為(1.5,0.63,0.5)，如圖4所示。

表1 隨機取一組T/3數據

圖4 T/3數據每段的二分中點計算斜率形成的斜率編碼

3 正常序列、防夾編碼序列和劇烈顛簸編碼序列分類模型學習算法

3.1 利用跟隨周期子序列均值差值編碼分類正常和異常序列

利用跟隨周期均值顯著化序列異常數據的學習算法獲取最佳的子序列劃分長度T,同時得到區分異常和正常子序列的跟隨周期均值差值的閾值α，T要達到符合防夾力閾值的要求。學習算法的主要思想：

(1)把訓練數據集的每組整體信號序列按照周期T均勻劃分。

(2)計算每組分子序列的均值，得到每組整體序列的均值編碼

(3)T=T+Δt，重復(1)、(2)直到防夾子序列的漲幅積累最佳，同時正常子序列的漲幅積累要盡量與下降量抵消，α不再增加。驗證等詳見參考文獻[9]。

分類正常和異常子序列。按照學習到的周期T劃分整個待測序列，計算每一子序列的均值得到編碼序列

3.2 防夾、劇烈顛簸序列分類特征閾值的訓練算法與分析

4維編碼S(k1,k2,k3,k4)為一個向量，在[-90°,90°]斜率變化幅度內以0°為中心，隨角度變化斜率急劇變化是距離可分的，且距離成中心擴散分布狀態。閔可夫斯基距離可選其不同形式，以計算簡單為目的這里選歐式距離和曼哈頓距離，通過實驗對比可知，曼哈頓距離優于歐氏距離。距離衡量需要有參照點和分類閾值，因此，需要事先通過歷史數據學習找到合理的參照點c和距離分類的閾值供車窗防夾判斷算法使用。

(1)利用跟隨周期法分理出防夾和劇烈顛簸序列集，每個子序列帶有分類標簽l，0為劇烈顛簸分類，1為防夾分類。S異={s1{y1,y2,y3,…，y4T/3，l1},…,sn{y1,y2,y3,…，y4T/3,ln}};

選取部分數據如表2所示，進行實驗驗證。根據防夾序列距中心距離越收斂，劇烈顛簸序列距中心越發散，分類效果越好的原則，表中第2、第8初始點可為候選中心點，但是防夾和劇烈顛簸序列距離的最大、最小值差值分別為8.1和-5.1，若2為中心點則兩類數據區分空間鮮明，而8為中心點則兩類數據有交叉重合區域，最終選2為中心點。同時對比閔可夫斯基歐式距離和曼哈頓距離兩種距離均值，曼哈頓距離使兩類分類分離性更好，準確度更高，如圖5所示。ROC圖如圖6所示。經過中心點選取算法和ROC分析可以獲得分類模型的中心點C和分類距離閾值r。

圖5 4編碼防夾序列、劇烈顛簸序列距8個參照中心的閔可夫斯基歐式和曼哈頓兩種距離均值

圖6 4編碼夫斯基歐式距離和曼哈頓距離 圖7 部分防夾序列、劇烈顛簸序列分類 分類的ROC圖 距分類中心C的距離分布

表2 防夾序列、劇烈顛簸序列距相應初始點為參照中心的平均距離

3.3 防夾、劇烈顛簸序列的分類特征閾值的驗證

在測試集里驗證2.1中學習到的閾值和分類中心的效果，分別計算測試數據編碼序列與選定中心點C的距離如表3所示。距離分布如圖7所示。空心點為劇烈顛簸序列與中心點距離，非空心點為防夾序列與中心點的距離，由圖7可見，兩類點有明顯的分類特征，且防夾序列距離中心的距離全部落在閾值之內。分類距離不同閾值測試結果的評價指標如表4所示。

表3 部分測試數據編碼序列與選定中心點C的距離

表4 分類距離不同閾值測試結果評價指標

3.4 車窗行進時霍爾信號序列流子序列的分類樹模型

圖8 霍爾信號序列流分類決策CART樹 圖9 車窗行進時序列流的防夾判斷原理圖

4 車窗行進時序列流的防夾判斷算法設計

4.1 算法工作原理

算法首先需要讀取并緩存待測序列流，進行異常檢測，如有異常，由異常分類特征分離出防夾或劇烈顛簸，防夾情況則進行防夾處理，所有其他情況通知緩管道模塊讀取并更新相應數據，工作原理圖如圖9所示。

4.2 具體算法步驟

算法的必要數據設計需要緩存待測序列數據流，緩存數據的個數為2T，且為整數，T為跟隨周期，設為s1(y1,y2,y3,…，yT)和s2(y1,y2,y3,…，yT)；緩存序列編碼后的一個子序列，設為s′(k1,k2,k3,k4)，包含4個實數；參照中心序列(與s′相同編碼的序列且有初始值),設為c(k1,k2,k3,k4)；異常判斷閾值為1個整數，設為α；分類判斷距離閾值為1個整數，設為r。防夾算法的具體步驟：

(1)讀取2T個待測序列信號預處理后，分別存入s1、s2；

(2)計算s1、s2的均值之差，如果大于閾值α，則出現異常，跳到步驟(5)；

(4)進行防夾處理，跳到步驟(1)；

(5)s1=s2，重新讀取待測序列信號預處理后存入s2，返回步驟(2)。

由于參數T、α、c、r為離線訓練得到，真正防夾算法的時間、空間復雜度小于o(3T),實驗得出T為均小于80的整數。

5 結語

基于積累周期分段編碼的汽車車窗防夾判斷算法，利用數據本身蘊含的規律有效地提高了實時防夾檢測的準確率，同時對外界干擾抵抗力良好，算法時間空間復雜度低，防夾定位穩定，對序列幅度數據的統計分布無要求；對于軟件設計人員無需清楚硬件原理和復雜的車窗受力推導計算，只需關注信號的數據規律和軟件設計。其簡單高效、魯棒的特點，尤為適宜實時監測硬件受限的應用場景，但是序列的時序維度要滿足均勻分布的要求，例如點擊事件序列流數據不適用。