基于復合置信度的不確定條件下循環水系統優化

王藝慧，王彧斐*，馮 霄，韓一杰

（1.中國石油大學（北京），重質油國家重點實驗室，北京 102249；2.西安交通大學，化學工程與技術學院，西安 710049;3.國能經濟技術研究院有限責任公司，北京 102200）

作為化工行業中重要公用工程的循環冷卻水系統，需要耗費大量的電能來維持風機和泵網絡的運轉以保障系統的穩定[1-2]。其用水量大約占到了工業用水量的七成。因此，循環冷卻水系統的優化對于化工行業實現節能節水具有重要的指導意義。

目前循環冷卻水系統的優化問題研究主要集中于優化系統的各個部件，如GOLOLO 結合冷卻器網絡壓降、冷卻塔操作、管路費用以及操作費用等多素，針對涉及多個冷卻塔和冷卻器的循環水系統，通過對管路和冷卻器壓降方程、管路費用、泵和風機的操作費用線性化，提出了一種混合整數線性規劃模型，該模型可使優化后的循環水系統收益最大化[3]。SUN 等提出了1 種主輔泵網絡結構，通過在指定支路上安裝輔泵，使主泵壓頭不需要大于所有冷卻器最小壓頭需求，從而實現泵壓頭減小和泵運行成本的優化[4]。CUI 等對冷卻塔的噴淋系統進行了優化[5]。還有部分學者對冷卻塔進行了實驗研究和數值分析，提出了關于冷卻塔設計的新想法，如多塔系統設計[6-7]。同時還有部分學者考慮了泵網絡和冷卻器網絡的聯合優化。SUN等提出2步法，首先將并聯冷卻器網絡轉變成串并聯結構，在規定冷卻器網絡結構和限制水流量的基礎上進行泵網絡的優化，并在支管上安裝輔泵[4]。

以上提及的循環水系統優化大都假設參數固定，優化后的系統存在較大的改進空間。但實際操作過程中，許多參數存在著明顯的不確定性。PISTIKOPOULOS 將不確定參數分為4 類并針對一般不確定性問題建立了模型[8]；GROSSMANN 則對當前各種優化方法經歷的發展問題給出了建議和解決方案[9]。CHEN等基于近10年的不確定性模型相關研究，主要介紹了3種解決不確定性的方法[10]。在這些學者的研究基礎上，在具體的水資源配置問題上，王彪等假設水資源優化配置中參數波動皆服從正態分布，并在優化程序引入病毒遺傳算法，以區域水資源配置效益最優和染色體年齡最大為優化目標進行配置研究[11]；李建美等采用基于參考點選擇機制的遺傳算法NSGA-III 求解紅延河調水工程的多目標配置模型得到受水區水資源配置的Pareto優化解[12]。杜佰林等在水資源優化配置中探尋新的求解方法，將模擬退火的思想引入基本粒子群算法當中[13]。

本研究進行動態條件下系統的優化問題，選取熱物流的流量為不確定性參數；就如何平衡系統經濟性和安全性問題，基于工藝要求，分別為十股物流選擇合適的置信度。對比分析確定條件下和基于復合置信度的不確定條件下得出的優化結果，得到了最佳網絡配置。

1 問題的提出

研究了1個考慮空氣冷卻器和串并聯冷卻水網絡的系統，如圖1所示。

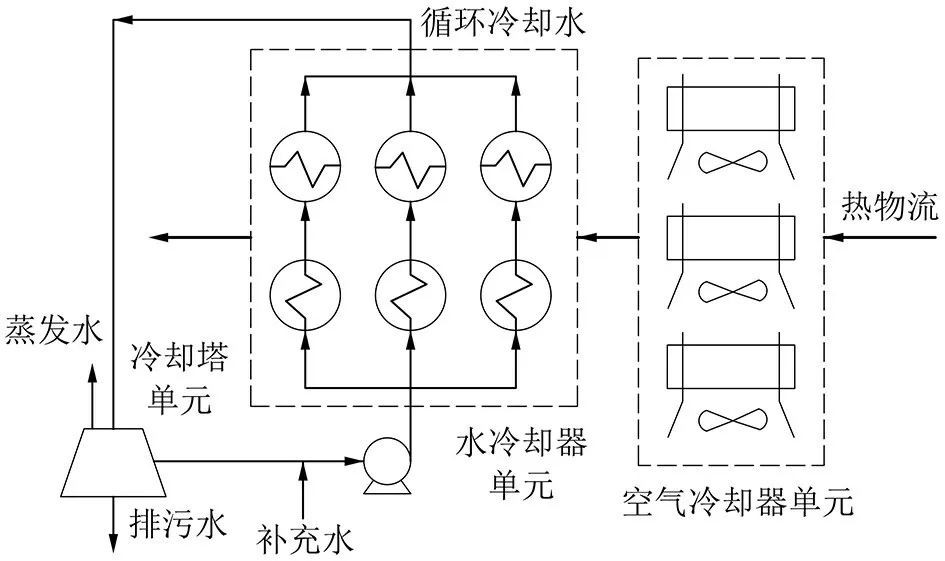
圖1 循環冷卻水系統結構Fig.1 Structure of circulating cooling water system

給出冷卻目標后，熱物流在空氣冷卻器中完成一次冷卻后再由水冷卻器進一步冷卻，以達到目標溫度。完成冷卻任務后的高溫冷卻水返回到冷卻塔中降溫以保證循環使用，并且冷卻塔中部分冷卻水存在排污和蒸發損失，因此需要等量補水。本工作中，給出了10 股熱物流的初始溫度、目標溫度和熱容量。熱物流首先由空氣冷卻器冷卻到一定溫度，然后由水冷卻器冷卻到規定量。為減少冷卻水的流量，前面水冷器使用過的冷卻水順流到另一個水冷卻器中，達到節水的目的。

在循環冷卻水系統的管理和規劃中，許多參數在整個運行期間存在著明顯的動態性、復雜性以及不確定性，這些不確定性參數將會影響循環水系統模型的構建與求解。在本系統中，工藝熱物流由于存在波動而使得其流量不斷變化，導致空冷器和水冷器間的熱負荷分配隨之變化，故將熱物流的流量看作不確定性參數。考慮不確定性參數后的循環水系統，目標函數相應的成為了不確定變量，由于需要合理規劃冷卻器的排列形式，還會存在部分整數變量，故整個問題轉變成混合整數非線性問題的求解。對于不確定性優化問題的求解，采用機會約束規劃構建模型并基于蒙特卡洛算法解決MINLP問題。

循環水系統以最小化總成本為目標函數，總成本是系統各部分成本的總和，包括空冷器成本，水冷器成本，泵的總成本以及冷卻塔成本。具體方程為：

2 模型的建立

2.1 空冷器

在循環冷卻水系統中，熱物流首先經過空氣冷卻器進行降溫，空氣冷卻器以環境空氣為冷卻介質來實現冷卻過程。空氣冷卻器模型常數Ca：

式中，Thin(i)和Thaout(i)分別為熱物流i在空氣冷卻過程中的進出口溫度，Fh(i)為熱物流i的質量流量，這是不確定性參數。Ta和Thaout(i)分別為空氣冷卻器i的進口空氣溫度和出口空氣溫度，Fa(i)是空氣冷卻器i中用以冷卻熱物流的空氣流量。

空氣冷卻器i兩側熱物流的溫差：

即要求兩側溫差應該大于空氣冷卻器的最小溫差ΔTmin。式中，Ta為空氣冷卻器入口處的空氣（環境）溫度，影響空氣冷卻器的表面速度，vNF和vF分別為空氣冷卻器的實際表面速度和表面速度[11]。

空氣冷卻器的操作成本是指運行冷卻器所消耗的電力成本。空氣冷卻器操作成本的計算：

式中，Pfa(i)為空氣冷卻器i的風扇電力功耗，Δpa為空氣冷卻器風扇壓降，pe為電費，t為操作時間。ηaf為空氣冷卻器中的風機效率。

空氣冷卻器風扇消耗的能量主要取決于空氣冷卻器的空氣體積流量、風扇壓降和風扇效率。Δpa的計算：

式中，ff為空氣冷卻器風扇的摩擦系數，Nb為空氣冷卻器中的管程數，Gmax表示流經空氣冷卻器狹窄部分時空氣的最大速度，G為空氣的流速，ρair為空氣密度。

空氣冷卻器的總成本費用在計算過程中會受到不確定參數的影響，所以其在不確定條件下是變化的。

2.2 水冷器

計算水冷卻器總成本時只需考慮投資成本。計算方法：

式中，dtwin(i)和d twout(i)分別為水冷卻器兩側熱物流與冷卻水的溫差，要求其應大于水冷卻器的最小溫差ΔTmin。

2.3 冷卻水網絡

為了提高冷卻水的回水溫度和冷卻塔的效率，降低冷卻水的流量，考慮采用串并聯結構的冷卻水網絡。模型中含有一定的約束條件，用以表示進出口物流之間的關系。

Z(i,j)是一個二元變量，描述不同水冷卻器之間的連接關系，表示冷卻器E-i是否將出口冷卻水送至冷卻器E-j。每個冷卻器，比如冷卻器E-i，只能將出口冷卻水送至下1個冷卻器或將使用過的冷卻水送回冷卻塔中[14]：

當冷卻器的冷卻水來源是冷卻塔中的新鮮水時，冷卻器E-i的入口溫度和入口水流量則為新鮮冷卻水的溫度和流量。當冷卻器接受來自其他冷卻器E-j的回用水時，此時冷卻器E-i的入口溫度則為E-j的出口水溫，便不再接收來自冷卻塔的新鮮冷卻水。

冷卻水總質量流量的計算：

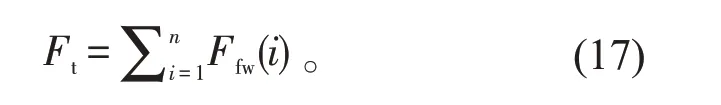
即冷卻塔送至冷卻器所有鮮冷卻水的質量流量之和。

當計算公式中存在不確定性參數時，冷卻水網絡的結構可能也會隨之變化，產生的費用也會不同。

2.4 泵網絡

為了將冷卻塔中的冷卻水送至各個冷卻器中，需要水泵的輸送。水泵的成本計算：

2.5 冷卻塔

冷卻塔的總成本包括冷卻塔的投資費用Ctc和冷卻塔的運行成本Cto：

影響冷卻塔性能和成本的因素有很多，包括局部空氣濕球溫度、空氣濕度、大氣壓力、空氣流量、水流量及進出口溫度等。

其中冷卻塔的運行成本包括風扇的運行成本、補給冷卻水的總成本、排污水處理成本以及化學處理費用。在系統運行過程中，在塔底部會聚集一些礦物質和雜質，因此需要將部分冷卻水排空，以保持冷卻塔能正常操作運行。在工作過程中會存在部分冷卻水蒸發，為保持水流量的穩定，應在系統中及時補充冷卻水。冷卻塔的運行成本的計算：

式中，Ctof為冷卻塔的風扇費用；Ft為冷卻水的總質量流量，作為本系統中重要的優化參數，水流量的減少可以顯著降低冷卻塔的費用；Fb和Fm分別為排污水和補給水的質量流量，二者一定程度上可以反應優化后的效果；pm是新鮮補給水的價格，t為年運行時間。

冷卻塔風扇費用的計算：

式中，Qto是冷卻塔的總熱負荷，相當于所有水冷卻器熱負荷之和；cp為冷卻水的比熱容。

3 算法設計

選用機會約束規劃方法作為求解不確定條件下優化問題的工具。它一定程度上允許所作決策不滿足約束條件，但該決策應使約束條件成立的概率不小于某一置信水平α，從而保證系統的正常操作[15]。

機會約束規劃模型的求解通常是在已知的置信水平和隨機變量概率分布函數的條件下，通過將方程中的目標函數和約束條件轉化為與確定性問題相對應的且可以運行的等價模型進行求解。為了降低計算難度，避免復雜的變換過程，采用一種新的基于蒙特卡羅算法的機會約束規劃方法。Gams 軟件負責目標函數的編寫以及算法的調用。

根據確定條件下的流量設定波動范圍，保證各流股在流量范圍內的概率大于規定的置信度，運用Gams軟件對這10組約束建模，得到復合置信度的不確定條件下目標函數的變化，獲得優化的冷卻網絡配置。

4 案例研究

為驗證模型的有效性，以MA等的1個案例來說明[16]。共有10 股熱物流，物理參數和經濟參數已知。主要考慮2 種兩種情況系統的設計和優化：確定條件下的優化和基于復合置信度的不確定條件下的優化。

4.1 確定條件下的優化

表1給出了熱物流流量、進出口溫度和傳熱系數的數據。當空氣溫度為25 ℃，熱物流特征參數固定時，得到了確定條件下的最佳循環水系統優化設計。

表1 熱物流參數Tab 4 Hot stream parameters

優化后的冷卻系統熱物流首先經過空氣冷卻器冷卻到一定溫度，后被水冷卻器冷卻到目標溫度，實現換熱。10 股熱物流進口溫度相對較高，它們與空氣之間的溫差足以完成部分冷卻任務。與僅使用水冷卻器的系統相比，空氣冷卻器的使用減少了對循環水的需求和用量。

采用串聯水冷卻器結構，提高了最終回水溫度，減少了循環水的用量，水冷卻器最終出口溫度約為55 ℃。在這種情況下，使用了9 個空氣冷卻器，少于水冷卻器的數量，導致水冷負荷比例高，空冷負荷比例低。并且在設計過程中只考慮了經濟性，不涉及水資源和環境問題，所以水冷卻部分承擔較多的冷卻任務。

4.2 復合置信度的不確定條件下優化

實際生活中，物流在系統中的流動并不是一成不變的，往往其流量會偏離預期量。所以考慮熱物流的流量為不確定性參數，熱物流流量波動數據可以用均勻分布函數擬合。采用機會約束規劃來解決不確定條件下的優化問題，置信水平越高說明決策的保守性越強，系統會保持更穩定更可靠的操作，但其經濟性可能會不佳。機會約束規劃通過量化系統盈利性和可靠性之間的關系，為決策者提供了符合約束條件的置信水平和滿足經濟要求的綜合信息。

在考慮物流波動這一不確定性條件下，通過運行軟件得到的數據可知，當物流設置的波動區間越大，較確定條件下的總成本來說，增長的越多。波動區間每增加1 個單位會造成總成本1.16%的增加。這是因為熱物流流量發生變化后，經換熱器冷卻過程中相應的熱負荷隨之改變，從而增加了換熱器的換熱面積，影響了總成本的大小。

由于不同的物流波動對于系統的影響各異，故通過選取不同的置信度來表達流股波動程度的大小，不同的置信度會根據優化要求給出不同的輸出。故基于復合置信度的不確定條件下對循環水系統進行優化。

首先，為了分析單股物流波動對優化系統所消耗的總成本的敏感性，保證其他流股流量固定，采用機會約束規劃模型為所要研究的流股設定不同的置信度，運用Gams 軟件分別得到10 種情況下總成本隨置信度α的變化曲線，結果如圖2所示。

圖2 10股物流波動范圍內的影響Fig 2 The influence within the fluctuation range of ten streams

由圖2可知，當考慮流量的不確定性時，部分物流的置信度對成本沒有很大影響，曲線變化幅度不大。而有些物流的置信度會對成本產生較大影響，差值較為明顯。原因在于，物流本身的流量和溫度不同。對于本身溫度較低且流量較大的物流來說，發生流量波動后，冷熱物流間的傳熱驅動力較低，對系統的影響較小，總成本的變化不如高溫低流量的物流明顯；其次，每股物流設置的波動范圍不同，一些物流在隨機生成的流量范圍內只發生小幅波動，造成熱負荷的變化較小，因此總成本的變化沒有那么明顯。

通過分析10 股物流波動范圍內的影響曲線，綜合經濟性和可靠性2 方面，分別為10 股物流選擇了不同的置信度。此外，在實際工業過程中塔頂冷凝器有時會需要冷卻水進行冷卻，一旦冷卻負荷不滿足工藝要求，就會影響產品分離效果，從而對整個生產產生影響，因此面對動態的外部參數，此類物流的冷卻過程需要更加穩定，故針對這類物流直接指定較高的置信度。而針對其他的產品物流，冷卻負荷的波動并不會造成嚴重的不穩定生產，故可根據前面的分析，采用更為合適的置信度。在綜合考慮圖表的結果與結合實際狀況后，假設第2 股物流和第10 股物流為指定置信度的物流并分別為其設定為0.95。

結合圖表以及實際應用過程，分別為每股物流選出了最合適的置信度，使10 股熱物流在一定的流量范圍內變化且滿足在指定范圍內的概率大于等于選擇的置信度，故得到了10 個機會約束規劃的形式。在滿足等式（38）的概率（Pr）約束下，對系統進行優化。

式中，Fh為熱物流質量流量。

復合置信度下的優化結果包含9個空氣冷卻器和4 對串聯的水冷卻器，除了第2 股物流和第8 股物流以外，所有流股均由空氣冷卻器和水冷卻器進行雙重冷卻。空氣冷卻器出口溫度為64.9～113.6 ℃，當流股的溫度高于113.6 ℃時，采用水冷卻器來冷卻經濟性較差；在溫度低于64.9 ℃時，通過空氣冷卻器來冷卻熱物流是不合適的。冷卻器的排列形式與確定條件下的優化結構存在不同，部分流股僅憑借空氣冷卻器便能冷卻到指定溫度，空氣冷卻器的換熱面積明顯高于確定條件下。結果的主要差異是由于在不同的研究條件下，考慮流量的波動使得空冷器和水冷器的熱負荷分配發生了改變，為實現復合置信度下的最佳優化，換熱器的面積的變化引起水冷器串并聯結構不同于確定條件下。此外，物流發生波動后經過水冷卻器的物流出口溫度降低，這也促使水冷器的換熱面積減小，影響了冷卻器的排列布置。

5 結果與分析

表2顯示了2種案例的優化網絡配置參數的計算結果。

由表2可知，優化系統的差異主要體現在水冷卻器的數量、水冷卻器的連接方式、冷卻器的換熱面積、冷卻塔的總水流量等方面。這主要是因為考慮了物流流量的波動，10 股物流由于本身特性以及波動區間各異，導致在不確定條件下水冷卻器和空氣冷卻器的熱負荷分配發生了變化，從而引起換熱面積的改變。同時，針對流股對系統影響程度的大小，選擇不同的置信度，會比確定條件下經濟效益更可觀。基于復合置信度的不確定條件下的優化結果中，水冷卻器的排列方式改變，僅用9個水冷卻器便能完成冷卻任務。且系統冷卻水的用量與確定條件下相比降低6.3%。冷卻塔進出口的溫差變小以及用水總量的減少使得蒸發水量減少了5.4%。排污水和補充水的用量也相應減小，使得冷卻塔的運行成本隨之降低。

表2 2種案例的優化網絡配置參數Tab 2 Optimal network configuration parameters of the two cases

為了進一步研究考慮不確定性參數的優化效果，比較了2種案例優化后的成本數據，相關結果如表3所示。

由表3可知，基于復合置信度的不確定條件下系統的總用水量低，故冷卻塔的總成本費用會相應降低。雖然新的配置會引起空冷器的總成本比確定條件下高出24289.00 美元，但由于冷卻塔的費用約占年度總成本費用的50%，故基于復合置信度下考慮物流流量波動可以節省107873 美元的冷卻塔費用。由于水冷器排列方式的變化以及循環水用量的減小，冷卻器間的壓降有所降低，從而減小了水泵的總成本。因此，在循環水系統研究過程中考慮熱物流流量這一不確定性參數，并根據波動效果采取不同的置信度，實現復合置信度的不確定條件下的優化，可以使每年的總成本降低10.0%。

表3 2種案例的優化成本Tab 3 The optimization cost of the two cases

綜上所述，基于復合置信度的不確定性下研究循環水系統，在完成相同冷卻目標的情況下，可以減少系統的總用水量，從而降低冷卻塔和水泵的費用，實現節水目標。并且還可以在一定程度上減少水冷卻器的數量，節約水冷卻器的投資成本。除此之外，綜合考慮物流波動幅度、冷卻要求以及對系統的影響程度，使得不確定性下的系統在滿足經濟性的同時還實現了操作的穩定性，更符合工業實際運行情況，應用性更強。

6 結 論

在考慮不確定性參數存在的情況下，研究了循環冷卻水系統的優化，之前的文章大多基于確定條件下展開討論，沒有涉及不確定性的問題。在這項工作中，熱物流的流量是本設計中的不確定性參數，同時，由于不同物流波動對系統成本產生的影響不同、本身冷卻要求各異以及設置波動范圍不同，因此根據各流股特點為其選擇了不同的置信度。基于復合置信度的不確定條件下，為了滿足循環水系統經濟合理和操作穩定的要求，采用機會約束規劃建立了MINLP 模型。設計了1 種新的基于蒙特卡羅的算法，將復雜的概率約束形式轉換成了Gams 軟件能求解的程序，降低了計算難度[17]。在Gams 的求解匯總信息部分可以看到，DICOPT被調用來求解這個模型，共耗時397 s。

通過對比分析確定條件下和基于復合置信度的不確定性條件下循環水系統的優化配置參數，可以發現在考慮熱物流流量后，流量波動會引起冷卻器熱負荷的變化，從而導致換熱面積的改變。為平衡系統的經濟性和安全性之間的關系，通過分析每股物流置信度與總成本的變化曲線，為10 股物流選擇了合適的置信度。復合置信度下的循環水系統冷卻器排列方式不同于確定條件下，水冷器的數量和換熱面積低于后者，冷卻要求主要集中在空氣冷卻方面。對比二者成本數據可知，基于復合置信度下考慮系統不確定性參數的優化，系統的總用水量相比確定條件下降低6.3%，水冷卻器的總成本、冷卻塔的總成本和水泵的成本均減小，年度總成本費用可降低10.0%，優化后的循環水系統具有良好的經濟性和安全性。