基于模糊神經(jīng)網(wǎng)絡(luò)的啤酒灌裝精度控制技術(shù)

劉 偉

(吉林電子信息職業(yè)技術(shù)學(xué)院電氣工程學(xué)院，吉林 吉林 132000)

隨著自動化技術(shù)的發(fā)展以及市場競爭的加劇，全自動灌裝機(jī)成為灌裝生產(chǎn)線上不可或缺的設(shè)備，在食品、醫(yī)藥等行業(yè)中扮演著十分重要的角色[1-2]。灌裝的效率和精度是衡量企業(yè)生產(chǎn)能力的重點指標(biāo)，但就實際生產(chǎn)而言，部分企業(yè)還依靠人工手動調(diào)整灌裝精度，生產(chǎn)效率低，生產(chǎn)成本高。雖然也有企業(yè)采用了自動化生產(chǎn)設(shè)備，但精度低、穩(wěn)定性差。

灌裝是啤酒生產(chǎn)過程中的關(guān)鍵環(huán)節(jié)。灌裝機(jī)系統(tǒng)復(fù)雜，控制要素多，既要實現(xiàn)對流量、壓力以及重量等指標(biāo)的過程控制，還要同步控制傳動系統(tǒng)的運動速度和位置[3]。傳統(tǒng)灌裝過程需要人工復(fù)檢，效率低，成本高，且采用的常規(guī)PID控制方法參數(shù)不能實時調(diào)節(jié)，有一定的局限性。因此，學(xué)者們[4-7]不斷將模糊算法、神經(jīng)網(wǎng)絡(luò)算法等先進(jìn)控制理念融入到灌裝過程中。其中，模糊控制具有抗干擾能力強(qiáng)的特點，能有效解決多變量、非線性等問題，但模糊規(guī)則的制定受主觀因素影響大，缺乏自學(xué)習(xí)能力；神經(jīng)網(wǎng)絡(luò)控制是模擬人腦結(jié)構(gòu)機(jī)理來實現(xiàn)對復(fù)雜系統(tǒng)的控制，具有很強(qiáng)的自學(xué)習(xí)能力，但不適用于表達(dá)基于規(guī)則的知識，容易陷入局部最優(yōu)問題。

針對飲料產(chǎn)品自身特點及食品生產(chǎn)要求，研究擬將模糊算法與神經(jīng)網(wǎng)絡(luò)算法相結(jié)合，提出一種模糊神經(jīng)網(wǎng)絡(luò)PID(FNN-PID)控制策略，使系統(tǒng)既具備推理歸納能力，又具有自適應(yīng)能力，從而實現(xiàn)PID參數(shù)的動態(tài)調(diào)整，旨在為提高啤酒灌裝機(jī)的精確性和穩(wěn)定性提供依據(jù)。

1 灌裝機(jī)結(jié)構(gòu)及工作流程

灌裝機(jī)工作流程包括清洗、傳送、灌裝、封裝等，其中灌裝是灌裝機(jī)的核心工序[8]。灌裝機(jī)構(gòu)主要由傳送帶伺服機(jī)構(gòu)M1、灌裝伺服機(jī)構(gòu)M2、稱重裝置、液體充灌裝置以及重量檢測裝置等組成(圖1)。

圖1 灌裝機(jī)結(jié)構(gòu)Figure 1 Structure of filling machine

該灌裝機(jī)采用重力式灌裝方式，分為稱重區(qū)、灌裝區(qū)以及檢測補(bǔ)灌區(qū)3個工位。為提高灌裝速度，共設(shè)5個主灌裝接頭和5個補(bǔ)灌接頭，可根據(jù)生產(chǎn)需求在觸摸屏上設(shè)置傳送帶速度、灌裝重量以及灌裝時間等參數(shù)。當(dāng)按下啟動按鈕后，傳送帶將稱重后的空瓶送至灌裝區(qū)，灌裝接頭下降至灌裝位置，開啟閥門，完成初次灌裝任務(wù)。受泡沫、噴濺等因素影響，灌裝的容積或重量存在一定誤差，因此灌裝完成后，需對灌裝結(jié)果進(jìn)行精度檢測，不滿足條件的需進(jìn)行二次灌裝。試驗?zāi)康氖球炞C控制策略在灌裝機(jī)上的應(yīng)用效果，因此只對二次補(bǔ)灌過程進(jìn)行控制，以重量偏差為研究指標(biāo)，具體灌裝步驟為：

(1) 稱重區(qū)進(jìn)行空瓶稱重，并確認(rèn)是否有灌裝瓶。

(2) PLC控制伺服電機(jī)M1帶動傳送帶將待灌裝的空瓶傳送至灌裝區(qū)。

(3) 伺服電機(jī)M2驅(qū)動灌裝接頭下降至灌裝位置。

(4) 按照設(shè)定參數(shù)開始第一次灌裝。

(5) 初次灌裝完成后，傳送帶將灌裝好的飲料瓶送至檢測區(qū)，并將未灌裝的空瓶同步送至灌裝區(qū)，做好下一次灌裝準(zhǔn)備。

(6) 對已灌裝的飲料瓶進(jìn)行重量檢測，計算瓶內(nèi)液體的重量。

(7) 計算重量偏差，采用FNN-PID控制器進(jìn)行二次補(bǔ)灌。

(8) 當(dāng)檢測值與設(shè)定值相同時，灌裝完成。

2 控制系統(tǒng)設(shè)計

2.1 控制系統(tǒng)組成

控制系統(tǒng)由上位機(jī)、PLC控制器、傳感器、伺服電機(jī)、驅(qū)動器以及電磁元件等模塊組成(見圖2)。PLC控制器是系統(tǒng)的核心，在收到傳感器采集的流量、位置、重量等數(shù)據(jù)信息后，根據(jù)設(shè)計要求向執(zhí)行元件發(fā)送控制指令，控制伺服電機(jī)、電磁開關(guān)等執(zhí)行器工作[9-11]。上位機(jī)主要用來監(jiān)測灌裝過程，實現(xiàn)人機(jī)交互，具有參數(shù)設(shè)定、故障報警、數(shù)據(jù)監(jiān)控等功能。

圖2 灌裝控制系統(tǒng)組成Figure 2 Composition of filling control system

2.2 模糊神經(jīng)PID控制器結(jié)構(gòu)

為保證灌裝精度，需解決系統(tǒng)存在的時變性問題。模糊神經(jīng)網(wǎng)絡(luò)結(jié)合了模糊控制精度高和神經(jīng)網(wǎng)絡(luò)自學(xué)習(xí)能力強(qiáng)的特點，在控制參數(shù)發(fā)生變化時只需更新樣本數(shù)據(jù)重新訓(xùn)練即可，可移植性較強(qiáng)[12-13]。因此，采用模糊神經(jīng)網(wǎng)絡(luò)在線更新PID參數(shù)，模糊神經(jīng)網(wǎng)絡(luò)PID控制器結(jié)構(gòu)如圖3所示。

圖3 模糊神經(jīng)網(wǎng)絡(luò)PID控制器結(jié)構(gòu)Figure 3 Fuzzy neural network PID controller structure

試驗設(shè)計的模糊神經(jīng)網(wǎng)絡(luò)采用雙輸入結(jié)構(gòu)，輸入神經(jīng)元是灌裝重量的偏差和偏差變化率，輸出神經(jīng)元為PID的3個性能指標(biāo)參數(shù)Kp、Ki、Kd，包括輸入層、模糊化層、模糊推理層以及輸出層4個層級結(jié)構(gòu)(見圖4)。

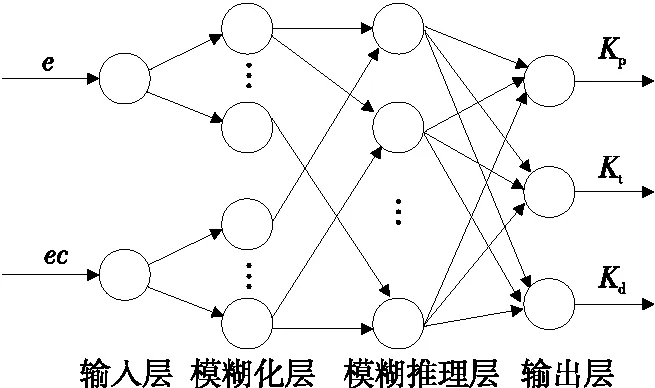
圖4 模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)Figure 4 Fuzzy neural network structure

(1) 輸入層：兩個輸入變量分別代表灌裝重量的偏差e和偏差變化率ec，分別對應(yīng)兩個神經(jīng)元節(jié)點，并通過激活函數(shù)輸出到模糊化層，其表達(dá)式為

f1(x1)=xi。

(1)

(2) 模糊化層：將輸入變量e和ec模糊化，利用高斯函數(shù)[式(2)]作為評價標(biāo)準(zhǔn)，計算各語言變量作為隸屬度函數(shù)的輸入變量，從而達(dá)到模糊化的目的。

(2)

式中：

cij、σij——高斯函數(shù)的中心位置和寬度。

(3) 模糊推理層：該層中節(jié)點和模糊規(guī)則是一一對應(yīng)的，作用是進(jìn)行模糊推理，用于計算每條規(guī)則對于各自節(jié)點的適應(yīng)度，所采用的激活函數(shù)為

(3)

式中：

N——神經(jīng)元之和。

(4) 輸出層：實現(xiàn)變量的反模糊化，連接PID控制器的3個參數(shù)Kp，Ki，Kd。所采用的激活函數(shù)為

(4)

即

(5)

式中：

ω——模糊推理層與輸出層之間的連接權(quán)重。

根據(jù)系統(tǒng)控制特點，采用Delta(x)函數(shù)確立學(xué)習(xí)規(guī)則，使用梯度下降法實現(xiàn)網(wǎng)絡(luò)訓(xùn)練的調(diào)控，進(jìn)行隸屬度參數(shù)及輸出權(quán)值的學(xué)習(xí)訓(xùn)練，實現(xiàn)系統(tǒng)自適應(yīng)和快速逼近實際值的目的，其目標(biāo)函數(shù)為：

(6)

式中：

r(k)——理想輸出；

y(k)——實際輸出。

2.3 模糊推理規(guī)則

將訓(xùn)練樣本輸入到模糊神經(jīng)網(wǎng)絡(luò)的輸入層中進(jìn)行離線訓(xùn)練，直到滿足設(shè)定要求。利用映射關(guān)系將模糊邏輯和神經(jīng)網(wǎng)絡(luò)相結(jié)合，將模糊規(guī)則、隸屬度函數(shù)轉(zhuǎn)化為模糊神經(jīng)網(wǎng)絡(luò)的權(quán)重，利用神經(jīng)網(wǎng)絡(luò)的自學(xué)習(xí)能力來修正權(quán)重，不斷逼近設(shè)定值，達(dá)到模糊推理的目的。

對模糊子集的語言變量進(jìn)行設(shè)置：定義模糊子集為{NB，NM，NS，ZO，PS，PM，PB}，即{負(fù)大，負(fù)中，負(fù)小，零，正小，正中，正大}，e、ec的論域均為[-1，1]。控制規(guī)則是模糊控制器的核心，取決于專家的經(jīng)驗和推理。針對灌裝的工作特點制定ΔKp、ΔKd、ΔKi的模糊控制規(guī)則如表1～表3所示。

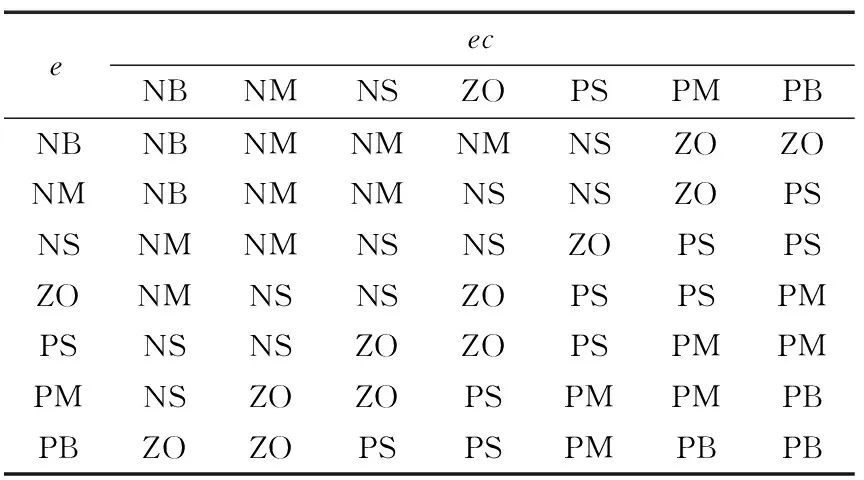
表1 ΔKp控制規(guī)則表Table 1 Control rule table of ΔKp

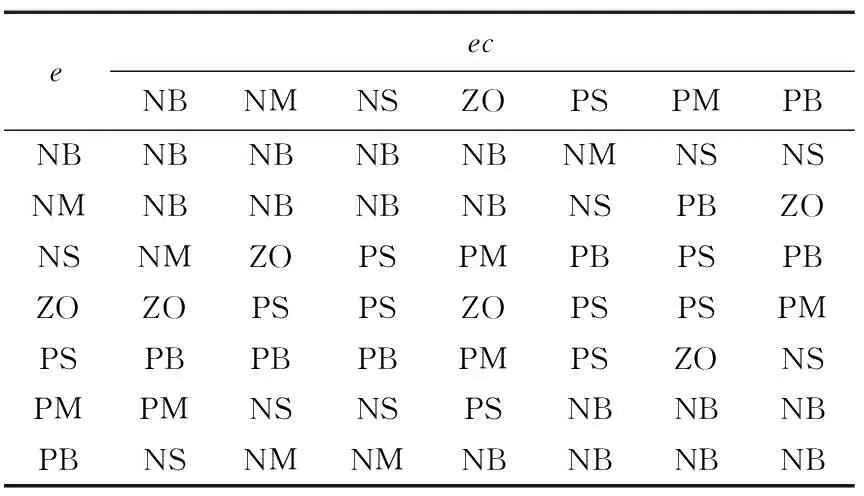
表2 ΔKi控制規(guī)則表Table 2 Control rule table of ΔKi

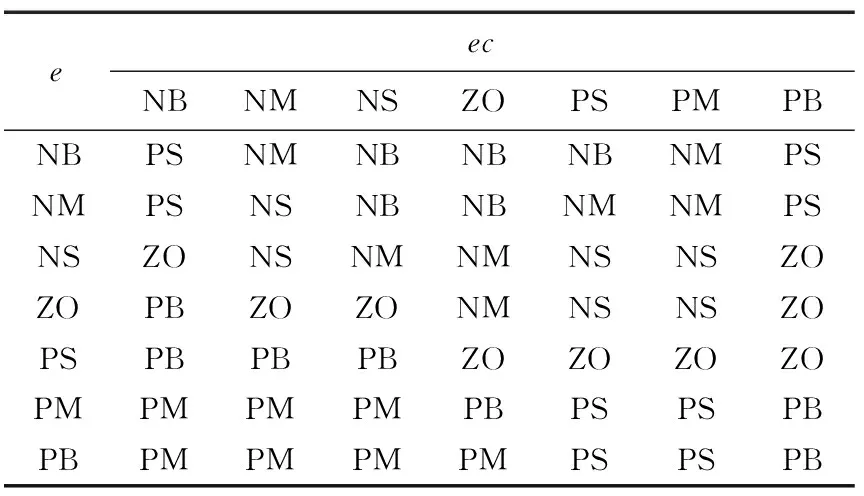
表3 ΔKd控制規(guī)則表Table 3 Control rule table of ΔKd

2.4 灌裝控制流程

將FNN-PID控制算法應(yīng)用于二次灌裝控制過程中，進(jìn)一步提高灌裝精度。在完成初次灌裝后進(jìn)入檢測區(qū)進(jìn)行稱重，根據(jù)兩次稱重結(jié)果計算灌裝液體的重量，利用測量值與目標(biāo)值之間的重量偏差進(jìn)行補(bǔ)灌控制，F(xiàn)NN-PID控制流程如圖5所示。

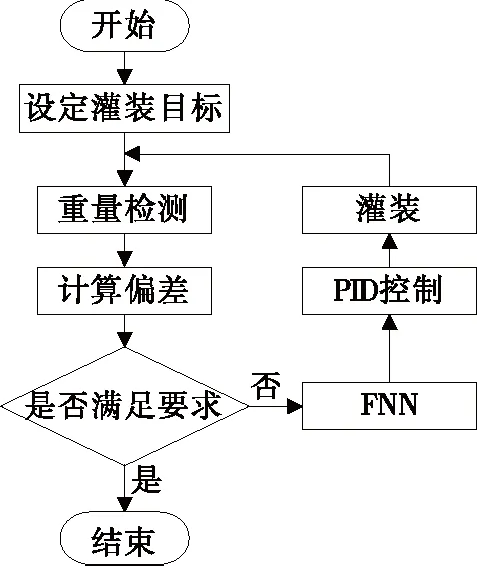
圖5 FNN-PID控制流程Figure 5 FNN-PID control flow

3 仿真與結(jié)果分析

為驗證所設(shè)計控制方法的有效性，在MATLAB軟件中使用Simulink建立仿真模塊，將FNN-PID控制算法調(diào)入模型中進(jìn)行階躍響應(yīng)仿真分析，并與常規(guī)PID及模糊PID進(jìn)行對比，結(jié)果如圖6所示。

為進(jìn)一步說明幾種算法的控制效果，將圖6中曲線進(jìn)行量化處理，從峰值時間、峰值、超調(diào)量、調(diào)節(jié)時間4個指標(biāo)進(jìn)行對比分析，結(jié)果見表4。

圖6 階躍響應(yīng)對比情況Figure 6 Step response comparison

由表4可知，與其他算法相比，F(xiàn)NN-PID算法超調(diào)量最小，達(dá)到穩(wěn)定狀態(tài)時僅需2.81 s。與常規(guī)PID控制相比，F(xiàn)NN-PID的超調(diào)量和調(diào)整時間分別提高了67%和55%，具有控制精度高、響應(yīng)速度快、魯棒性好等特點，符合灌裝生產(chǎn)高效、準(zhǔn)確的控制要求。

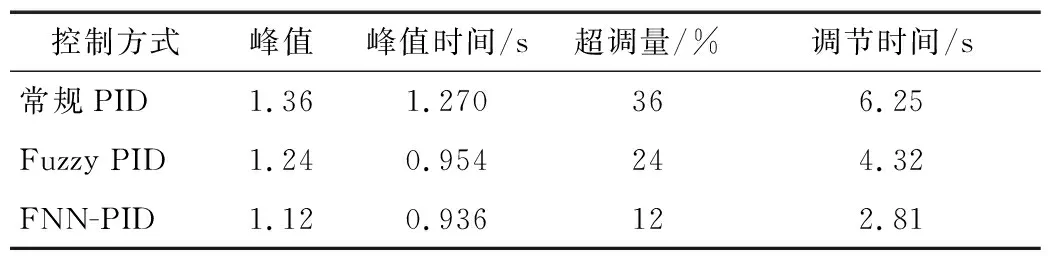
表4 仿真對比結(jié)果Table 4 Simulation comparison results

4 實驗驗證

搭建灌裝試驗平臺，因灌裝裝置只在補(bǔ)灌工序中實施了模糊神經(jīng)控制，所以測試中忽略初次灌裝工序，只對補(bǔ)灌流程進(jìn)行性能測試。試驗中先以100 g為目標(biāo)重量進(jìn)行灌裝，共進(jìn)行3組測試，每組測試分別采用常規(guī)PID、模糊PID以及FNN-PID進(jìn)行控制灌裝。每個補(bǔ)灌接口各灌裝12瓶，5個接口共灌裝60次，即3種控制方法各灌裝20次。要求灌裝精度為±3 g，產(chǎn)品合格率要求≥98.5%，灌裝完成后，在同一測量裝置上進(jìn)行稱量并記錄結(jié)果，忽略測量誤差，結(jié)果見表5。采用同一方法以200 g為目標(biāo)重量進(jìn)行第二次測試，要求灌裝精度為±5 g，產(chǎn)品合格率要求≥98.5%，結(jié)果見表6。

由表5可知，當(dāng)灌裝目標(biāo)為100 g時，PID控制平均灌裝誤差為2.0 g，最大絕對誤差為4.2 g；模糊PID控制平均灌裝誤差為1.5 g，最大絕對誤差為3.5 g；FNN-PID控制平均灌裝誤差為0.5 g，最大絕對誤差為0.9 g。由表6 可知，當(dāng)灌裝目標(biāo)為200 g時，PID控制平均灌裝誤差為3.5 g，最大絕對誤差為5.7 g；模糊PID控制平均灌裝誤差為3.2 g，最大絕對誤差為5.1 g；FNN-PID控制平均灌裝誤差為1.7 g，最大絕對誤差為3.2 g。從合格率角度看，3種控制方案的合格率分別為90%，95%，100%。為使分析更為直觀，將以上結(jié)果進(jìn)行繪圖對比(見圖7、圖8)。

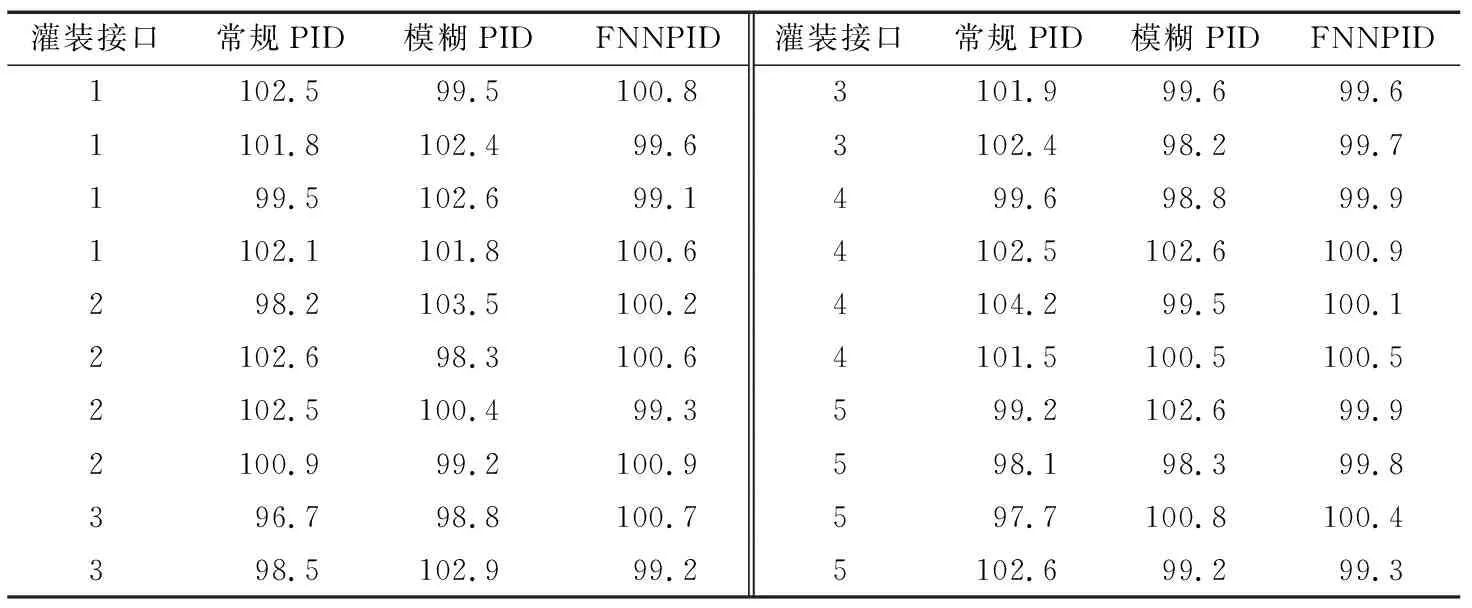
表5 灌裝目標(biāo)為100 g時的結(jié)果Table 5 Results of the filling target with 100 g

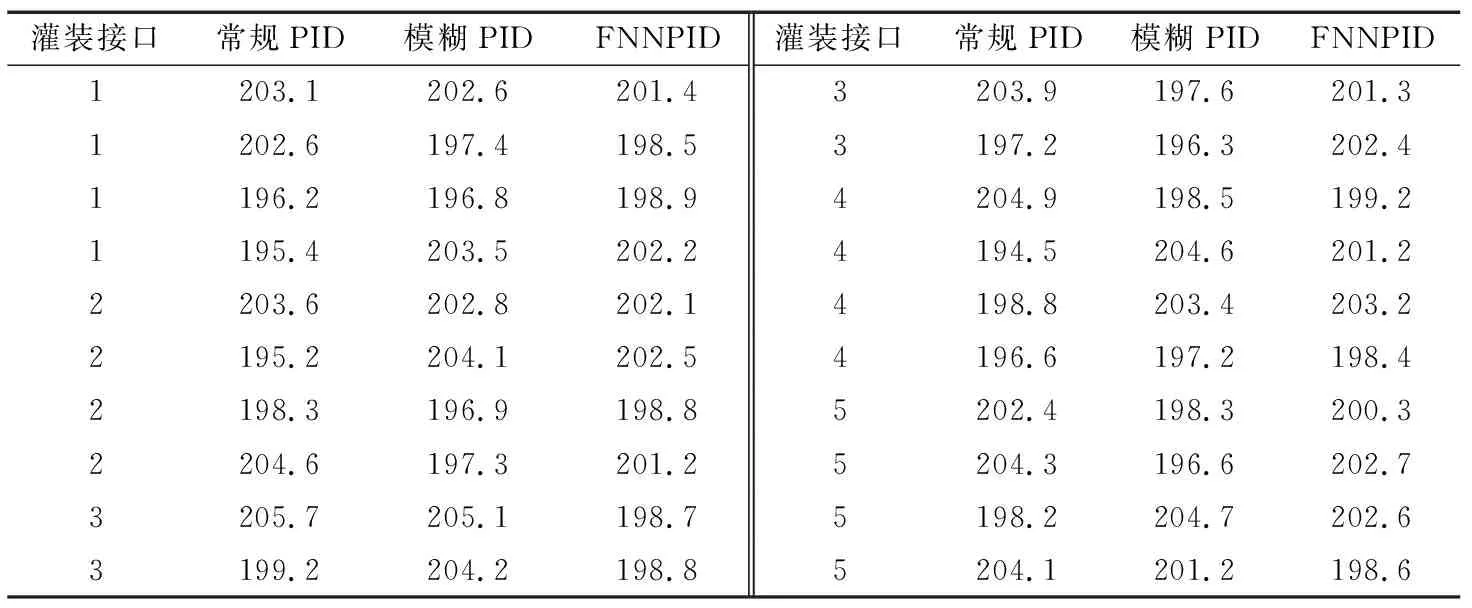
表6 灌裝目標(biāo)為200 g時的結(jié)果Table 6 Results of the filling target with 200 g

由圖7、圖8可知，F(xiàn)NN-PID控制精度高、穩(wěn)定性好，與常規(guī)PID及模糊PID控制相比，平均精度分別提高了49.5%，44.5%。

圖7 灌裝目標(biāo)為100 g時對比曲線Figure 7 Comparison curve of the fillin target with 100 g

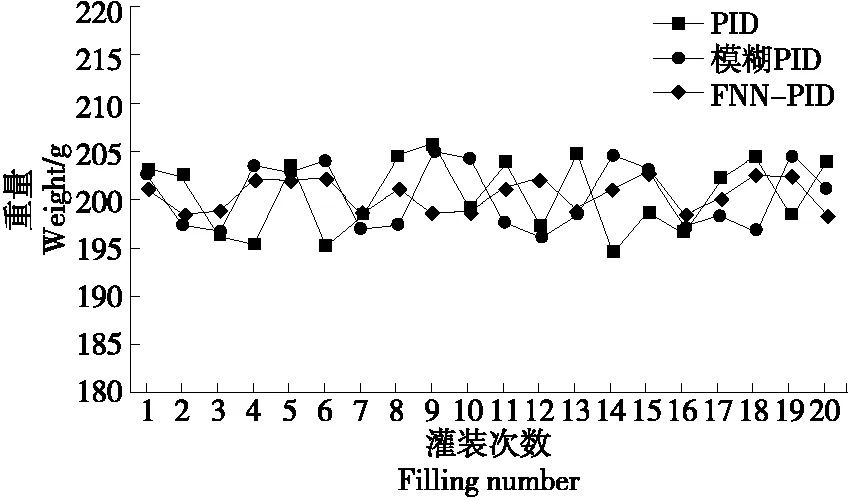
圖8 灌裝目標(biāo)為200 g時對比曲線Figure 8 Comparison curve of the filling target with 200 g

5 結(jié)論

以PLC控制為基礎(chǔ)，結(jié)合模糊算法抗干擾能力強(qiáng)以及神經(jīng)網(wǎng)絡(luò)算法自學(xué)習(xí)能力好的優(yōu)勢，提出了一種基于模糊神經(jīng)網(wǎng)絡(luò)的灌裝機(jī)PID控制算法，并將其應(yīng)用于飲料灌裝過程中。結(jié)果表明，基于模糊神經(jīng)網(wǎng)絡(luò)的灌裝機(jī)PID控制算法響應(yīng)速度快，相比常規(guī)PID控制提高了55%，可大大提高灌裝機(jī)的工作效率。基于模糊神經(jīng)網(wǎng)絡(luò)的灌裝機(jī)PID控制算法具有較高的控制精度，最大偏差僅1.7 g，灌裝合格率為100%，灌裝精度相比常規(guī)PID控制的提高了50%，滿足自動生產(chǎn)線運行穩(wěn)定、快速、可靠的要求。后續(xù)可對整個灌裝流程進(jìn)行優(yōu)化。