找出線索，層層突破

從名偵探福爾摩斯、柯南，再到我國唐代名相狄仁杰，他們都有共同的特點：智商超群，善于推理，查謎案于無蹤。為什么大家那么喜歡邏輯推理（常簡稱“推理”）故事呢？想必是那些懸疑叢生、謎團似錦的燒腦情節，激起人們對未知的好奇、對真相的探索、對正義的追尋。數學學科以抽象性、嚴謹性著稱，邏輯推理能力是數學課程要培養的核心素養之一，無論是數學知識的產生和發展，還是人們對數學知識的理解和運用，推理都在其中扮演著關鍵的角色，沒有嚴密的推理，就無法獲得準確可靠的結論。推理訓練題是培養學生邏輯思維、發展學生核心素養的有效載體。這里提供兩道趣味性強、有一定挑戰性的推理題，供讀者參考。

【題目】

題目1 破譯密碼

樂樂放學回家，發現家門開不了，心想應該是門鎖更換了密碼。于是拿出手機趕緊給爸爸發信息。你能根據以下爸爸和樂樂的對話信息，成功破解密碼嗎？

樂樂：爸爸，你換了我們家門鎖的密碼了？

爸爸：是啊！

樂樂：新密碼是多少？

爸爸：你不是總夸自己是小小福爾摩斯嗎？給你兩條線索，自己破譯吧！

樂樂：哈哈，好嘞！

爸爸：這兩條線索是——

樂樂：別賣關子啦！快點說。

爸爸：（1）密碼是個四位數，我連續五次輸入門鎖密碼，分別是：7152，9310，5274，2407，4721。（2）我每次輸入的密碼中有兩個數字正確，但所在的位置都不對。

題目2 撲克牌游戲

撲克牌是一種大眾娛樂工具。相傳早在秦漢相爭時期，大將軍韓信為了緩解士兵的思鄉之愁，發明了一種紙牌游戲。因為牌面只有樹葉大小，所以這種游戲被稱為“葉子戲”，后來紙牌發展成為現在的撲克牌。聰聰是玩撲克牌游戲的高手，一天，他設計了一個游戲和爸爸、媽媽一起玩。首先選擇了16張牌，將牌擺在桌子上（如圖1），隨后聰聰從16張牌中記下一張牌，將點數告訴了爸爸，將花色了告訴媽媽。

聰聰：爸爸和媽媽，你們能從已知的點數或花色中推知我記下的這張牌是什么嗎？

爸爸：我不知道這張牌。

媽媽：我知道你不知道這張牌。

爸爸：現在我知道這張牌了。

媽媽：我也知道了。

小朋友，聽了聰聰爸爸和媽媽的對話，你能推出這張牌是什么嗎？

【解析】

第1題，“破譯密碼”，聽上去有一種偵探破案的感覺。偵探具有很強的邏輯推理能力，他們特別善于從細節中捕捉破案的關鍵信息，循此展開推理，作出判斷。題目中給出了兩條線索，需要學生判斷從哪一條取得突破。第一條線索介紹了5次輸入的密碼，乍看好像推不出什么結論，可以先放在一邊。再仔細研讀第二條線索，根據“每次輸入的密碼中有兩個數字正確，但所在的位置都不對”，一下子可以找到兩個關鍵點，分別是“兩個數字正確”“位置不對”，到底是哪兩個數字正確呢？暫時看不出來，可以“位置”為突破口進行推斷。先將5個數豎著排，便于觀察：

這樣，根據兩條線索，抓取和解題有關的關鍵信息，思路就打開了。豎著排完以后，我們可以發現：2和7在每個位置都出現過，所以密碼中不可能有2和7，我們就可以根據第二條線索，運用排除法，排除每個密碼中的數字“2和7”，看剩下的數字是什么。根據7152這個數，可以知道密碼中必有1和5，根據5274可以知道密碼中必有5和4，根據2407可以知道密碼中必有4和0，根據4721可以知道密碼中必有4和1。從而得出密碼是由0、1、4、5這四個數字組成的。最后再次豎著觀察，用排除法來分析，得出密碼是1045。有時候線索的順序并不一定是“破案”的順序，根據線索找到關鍵信息才能有效突破，“細節決定成敗”用在“解題”中一樣有用。可以引導學生進一步思考：聰明的小福爾摩斯，假如密碼是5位，你能不能嘗試編一道密碼破譯題，也向你的爸爸媽媽提出挑戰呢？

第2題，聰聰設計的這個撲克牌游戲，要求從已知的點數或花色中推知心中想的這張牌，看似給了我們很多對話信息，可是容易被爸爸媽媽對話中的“不知道”“知道”弄迷糊。但細細來看，學生可以先從已有條件出發弄清題意，再逐條分析，抽絲剝繭地找到線索，完成推理。聰聰把點數告訴了爸爸，說明爸爸知道這張牌的點數；把花色告訴了媽媽，可見媽媽知道這張牌的花色。接下來可以把撲克牌游戲問題的這些條件轉化為數學的表示形式，為方便觀察和分析，可以把所有的圖片信息轉換成表格形式（如表1）。

我們可以把聰聰爸爸媽媽的對話和表格中的數對應起來看。爸爸知道的是這張牌的點數，但他說“我不知道這張牌”，表明他不知道的是這張牌的花色。基于這樣的理解，我們再去看表1，從中可以看出2、3、6、7、8、J、K這些數（J、K兩個字母分別代表11、13）所對應的花色是唯一的，比如2，只有黑桃里面才有2。如果爸爸拿到了這些點數的牌，他必能直接判斷這張牌的花色。但是爸爸說不知道這張牌，據此推理，可判斷爸爸所知道的點數肯定不是這些數，那只能是A、4、5、Q這四個之一，因為這四個點數所對應的花色至少有兩種（如表2）。比如A，紅桃里面有，方塊里面也有，只有這樣爸爸才不會猜出這張牌的顏色。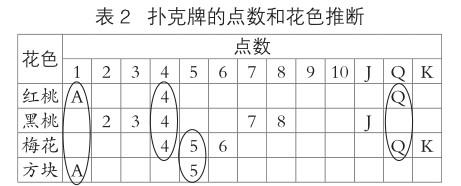

接下來從媽媽的話進行推理。她知道的是牌的花色，光憑花色就能很肯定地知道爸爸不知道，說明這個花色的所有牌的點數對應的花色都不止一種（否則知道點數的爸爸立即可以確定花色），可以斷定不是黑桃和梅花，爸爸就可以推出這張牌可能是紅桃或者是方塊，即可能是紅桃A、4、Q或者是方塊A、5。再看第三句：現在我知道這張牌了，爸爸光憑點數就能知道，說明這張牌絕不可能是A，因為A有兩張，不能確定是紅桃還是方塊。再次縮小范圍，還剩紅桃4、Q和方塊5，最后一句媽媽說：我也知道了，媽媽光憑花色就能知道，說明這張牌一定是同花色只有一個點數的那張，就是方塊5；如果是紅桃，就不能確定是4還是Q了。

【設計意圖】

邏輯推理屬于邏輯思維范疇，是一種理性認識，是人們運用概念、判斷、推理揭示事物本質和規律的認識過程，在人們的學習生活中占據重要位置。借助邏輯思維人們能預見事物的發展進程或現象將要發生的變化，作出合理、正確的判斷和選擇。邏輯思維是智力活動的核心成分，更是創造性思維的基礎。我們可以通過創設具體情境、點撥推理方法等途徑，進行推理訓練，培養邏輯思維，提升數學素養。

一、創設具體情境，驅動邏輯思維

小學生的思維正處于從具體形象思維逐步走向抽象邏輯思維的階段，往往需要在合適的情境或生活中感受和學習推理，驅動“邏輯思維”。數學中的邏輯推理訓練，需要教師創設學生熟悉的現實生活情境和形象生動的數學情境，以具體情境中的事物為載體引導學生開展非形式化推理活動，目的是讓學生認同邏輯推理這種思維模式。在上述兩道題目中，筆者都嘗試創設適合學生推理的具體情境，讓學生自然進入邏輯推理環節。比如，第1題“破譯密碼”，利用學生生活中常遇到的忘記密碼的情境，喚起學生想要“推理”的欲望，激起他們“推理密碼”的沖動，讓學生對對話中的數量關系作出思考分析，自然而然地開展推理，引發邏輯思維。再如第2題是從常見的撲克牌游戲進入推理環節，用學生熟悉的“撲克牌”設計了與以往不同的游戲，激發學生去探索、思考游戲結果，這就埋下了“推理”的種子。

二、點撥推理方法，發展邏輯思維

邏輯推理的基本步驟，就是根據已知的條件或前提，推斷出結論。當學生把現實生活或具體情境中的問題轉化為數學問題時，就進入到數學推理環節，這時需要運用多種操作和推理方法，而由于各種制約因素的存在，學生的方法積累相對不足，需要教師適時給學生提供方法指導，滿足不同學生群體的學習需要。小學生的思維特點，決定了推理能力的培養應當充分運用直觀、數形結合等方式，強化操作、實驗、猜想、驗證中的數學思考，從多方面促進理解、推理與表達。此外，推理需要運用敏銳的觀察力和洞察力展開深入思考和想象，才能形成豐富推理成果。比如，在第1題中，對于給出的兩條線索，如果按照順序，不一定能找到解題的思路，僅憑第一條線索得不到更多有用信息，此時，可以把該線索暫時擱置，引導學生從另外的線索中找到“兩個數字正確”“位置不對”兩個關鍵信息，從細節入手合理推斷，理清思路，按順序縱向列舉，通過觀察數字特征進行理智、系統的分析。再如，在第2題中，面對所列出的一大堆撲克牌，可引導學生先將現實問題轉化為數學問題，用符號語言和圖形語言把抽象的問題具體化。采用列表的方法，能夠清晰地看到對應的花色和點數，再根據對話中的表述，引導學生充分思考，逐條分析。每選擇1條信息，可以有2種推理方法，既可以從信息中找到符合條件的一些數或花色，也可以通過信息排除一些干擾，逐步縮小范圍。同時要注意關注邏輯順序。如，媽媽的表達之所以正確，是建立在“爸爸的表達是正確的”這個前提下。讓學生知道，前提是論證的基礎，推理常常是一環扣一環的。需要找出線索，再通過推理層層突破。

小學生正處于邏輯思維發展的啟蒙階段和黃金時期，教師可以有意識地進行推理訓練，培養學生的邏輯思維能力，提高思維的靈活性與嚴謹性，發展學生的數學核心素養。

（徐妍，江蘇省南京市長江路小學，郵編：210018）