配電網狀態估計可觀性研究綜述

韓平平，張 楠，潘 薇，吳紅斌

（安徽省新能源利用與節能省級實驗室（合肥工業大學），合肥 230009）

隨著社會經濟和可再生能源利用技術的迅速發展，越來越多的分布式電源與電動汽車規模化接入配電網，改變了傳統配電網單向潮流的基本格局，加劇了網架結構的復雜性，且電網運行狀態還將因分布式電源出力的隨機性而頻繁變化。配電網作為電力系統的終端，直接與用戶相連，其運行狀態直接關系到供電的可靠性。因此，及時準確地獲取配電網的實時狀態至關重要[1]。

狀態估計是實時感知和精細管控系統運行狀態的關鍵手段[2]。在運行系統中，狀態估計軟件由拓撲處理、可觀性分析、狀態估計和壞數據處理等模塊組成[3]。其中，可觀性分析是狀態估計的前提，是判斷已知量測數據是否能唯一確定系統狀態的過程。輸電網可觀性研究方法已較為成熟，對配電網可觀性研究起到了很好的借鑒作用。但是，相較于輸電網，配電網具有更大的節點規模、更多變的拓撲結構和嚴重的三相負荷不平衡問題等特點，使得適用于輸電網的可觀性分析方法和可觀度提高方案不能直接應用于配電網。由此可見，研究適用于配電網的分析方法和提高方案具有重要意義。此外，分布式電源與電動汽車的接入為配電網狀態估計可觀性帶來了新的挑戰。

綜上，本文依次對配電網可觀性分析方法、配電網可觀度提高手段、主動配電網偽量測建模技術的研究現狀和成果進行梳理和綜述，為解決實際系統存在的不可觀問題及后續研究提供借鑒與參考。

1 配電網狀態估計可觀性分析技術

1.1 狀態估計原理

電力系統中，在給定拓撲結構、線路參數和量測集合的條件下，狀態估計量測方程可表示為

式中：z為量測量矢量；h(x)為非線性量測函數矢量；x為狀態矢量；v為量測誤差。

狀態估計是根據量測系統冗余度和估計準則確定系統最可信狀態量的過程，提高了數據精準度與數據系統的完整性。在估計準則中，加權最小二乘準則應用最廣泛，其數學模型為

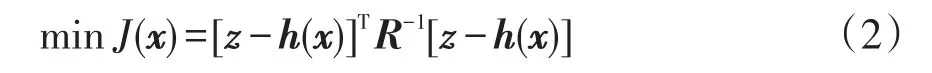
式中：J(x)為目標函數；R-1為量測權重。

可觀性分析是指分析能否通過已知網絡和量測集合進行狀態估計，確定系統的當前狀態。若通過可觀性分析判定量測正定或超定，利用已知量測可以完成狀態估計，則系統可觀；若通過可觀性分析判定量測欠定，狀態估計因缺乏必要量測而無法執行，則系統不可觀。系統的可觀度可以通過優化量測配置、偽量測建模或增加額外測量裝置等手段來提高。具體體現為：①生成滿秩的雅可比矩陣或滿秩樹，使得系統由不可觀變為可觀；②減小可觀系統中的不可觀風險指標值，使得系統的不可觀風險降低；③增加了可觀系統的可用量測，使得可觀度進一步提升，同時狀態估計計算結果的精度也得到提高。

1.2 配電網可觀性分析方法

目前配電網可觀性分析方法主要為數值法和拓撲法。數值法是通過信息矩陣能否完成因子分解且對角線不出現零主元或雅可比矩陣是否列滿秩來判斷網絡是否可觀，說明只有當線性無關的測量值數目大于或等于狀態變量數目時才滿足可觀條件。信息矩陣為

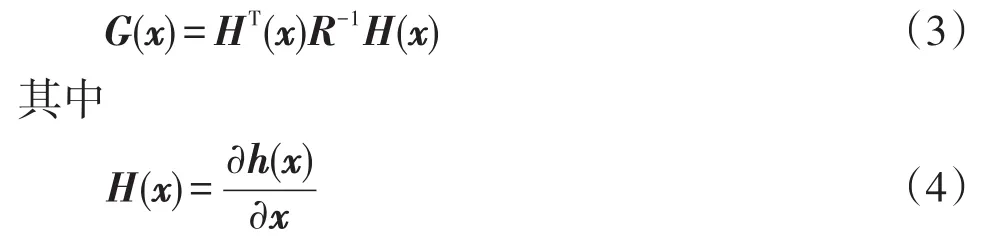
式中：G(x)為信息矩陣；H(x)為雅可比矩陣。

該方法具有避免迭代計算和無需額外編程的優點，在小型電力系統中應用較多。在輸電網中，相關文獻多從雅可比矩陣或信息矩陣的三角分解[4]、雅可比矩陣的零空間[5]、雅可比矩陣的Gram矩陣[6]等角度研究網絡可觀性，然而所采用的線性化解耦和單相建模的分析理論不能完全適用于阻抗比值大、三相耦合且不平衡情況較為嚴重的配電網中。基于此，文獻[7]提出基于正交線性變換的數值可觀性分析方法來解決配電網中阻抗比值大的問題。文獻[8]基于量測雅可比矩陣中P與V、Q、θ弱耦合，提出一種多相數值可觀性分析方法，為多相不平衡配電網的可觀性分析提供了思路。文獻[9]考慮了配電網中偽量測的位置和數量，對量測數據的優先級進行排序，并通過信息矩陣的三角分解進行可觀性判定，大大提高了分析效率。

拓撲法引入了圖論的思想，若能根據量測信息的搜索建立1個包含整個網絡所有節點的滿秩樹，則網絡可觀，否則網絡不可觀，此時可通過在較小樹之間添加可觀測分支來滿足可觀性。該方法避免了數值法中的浮點運算，分析速度快，廣泛應用于電力系統中。常用算法是先利用深度優先搜索法對有潮流量測的支路進行遍歷搜索形成多個可觀測區域，然后通過母線注入量測連通或擴大可觀測區域，形成可觀測島。可將電力系統看作僅由頂點和邊構成的圖R=(V,E)，V表示頂點集合，E表示邊集合，分別對應系統母線與支路的集合。可觀測島可看作1個測量子圖R′=(V′,E′)，若V?V′，即子圖R′包含了圖R中所有頂點，則可證明系統拓撲可觀。

現有拓撲可觀性分析方法相關研究多集中于最大可觀測島的生成和可觀性判定條件的選擇[10-12]。針對配電網相量測量單元較少的現狀，文獻[13]提出基于潮流定解條件的配電網可觀性拓撲分析方法，利用極少相角量測即可判斷系統是否可觀，文中所提方法也很好地適應了配電網輻射狀的結構特點。

但由于傳統的拓撲算法比較復雜，可能會出現組合爆炸問題。為解決此問題，有學者提出了一種拓撲-數值混合的可觀性分析方法。例如，文獻[14]首先利用拓撲法生成局部可觀測區域，然后添加最小數量的偽量測潮流分支，最后通過基于解耦直流模型的數值可觀性分析方法得到可觀性分析結果，該混合分析方法是由復雜環網運行特點和圖論中環的概念衍生，廣泛用于大規模環形輸電網，配電網中使用較少。

以上可觀性分析方法均是基于已有量測的數量、類型和位置來確定可觀性。然而部分配電系統中由于量測配置不足，還存在較多大誤差偽量測，即使通過分析方法確定網絡可觀，狀態估計結果也與網絡真實狀態存在較大差異，其表征該系統具有不合理的可觀性。通過概率分析方法可以解決偽量測帶來的不確定問題。例如，文獻[15]在高斯分布的假設下，首先通過計算信息矩陣的方式得到了相應的概率密度函數PDF（probability density function），計算公式為

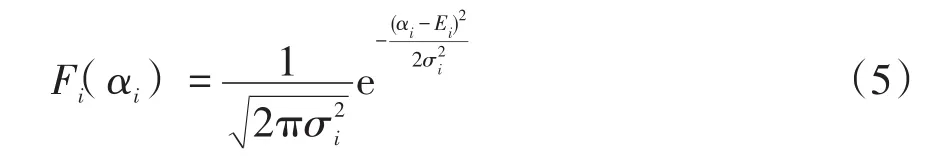
式中：αi為狀態變量可能的取值；Ei為狀態變量的估計值；為狀態變量的方差，由信息矩陣逆矩陣的對角線元素表示。

然后用概率密度函數對狀態變量置信區間進行計算，即

式中：αi_max、αi_min分別為置信區間上限、下限；CL為預先定義的置信度。

最后通過判斷各節點參數的置信區間與其所要求估計精度的關系來判斷網絡的可觀性。

配電網可觀性分析可以追溯配電網不可觀原因，從而為量測配置和偽量測添加提供針對性建議。總體而言，配電網的可觀性分析方法尚處于初步研究階段，如何將較為成熟的輸電網分析方法用于配電網將是未來的研究熱點。例如，隨著環網解耦研究的逐步深入，為拓撲-數值法應用于配電網提供了可能。相量測量單元在配電網中規模化接入也為拓撲法的應用創造了條件。

1.3 配電網可觀性評價指標

若確認系統可觀，則需要建立1個綜合的評價指標來表示不同量測集的可觀度。該指標依賴于數據冗余，數據冗余不僅與量測數量有關，還取決于量測類型和位置。傳統的定性可觀性分析難以準確表達出此指標的特性。基于此，有學者提出不可觀風險數值指標的概念，并對可觀性的評價指標進行量化，直觀地展現出不同量測系統的不可觀程度[16]。將量化指標擴展到三相，可得到配電網可觀性評價指標。

（1）不可觀風險指標A1為失去任意1個量測后導致網絡不可觀的概率，計算公式為

式中：m為三相總量測數；NCmeans為三相關鍵量測總數。在所有量測中，若某一關鍵量測丟失，則會導致系統不可觀。

（2）不可觀風險指標A2為失去任意2個量測后導致網絡不可觀的概率，可引入文獻[16]中關鍵量測組的概念，計算公式為

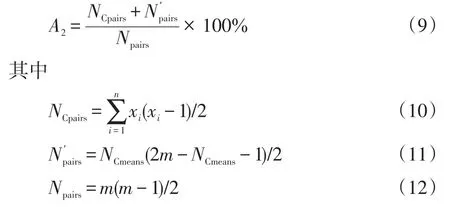
式中：NCpairs為關鍵量測組中任意失去2個量測的組合數；n為關鍵量測組的組數；xi為第i個關鍵量測組中的量測數；Np′airs為任意失去的兩個量測中至少含有1個關鍵量測的組合數；Npairs為任意失去2個量測量的組合數。關鍵量測組由部分量測量組成，在關鍵量測組中丟失任意2個量測會導致系統不可觀，丟失任意1個量測則不會導致系統不可觀。可見，關鍵量測組與關鍵量測相互獨立。

（3）不可觀風險指標A3為任意1個量測配置不可用（其所提供測量數據均丟失）后導致網絡不可觀的概率，計算公式為

式中：Nrtus為量測配置總數；NCrtus為關鍵量測配置數。若某一關鍵量測完全不可用，則會導致系統不可觀。

上述3種不可觀風險指標可以量化系統不可觀風險，數值越大風險越高[17]。不可觀風險指標計算的難點在于關鍵量測量和關鍵量測組的辨識。與輸電網相比，配電網節點和支路眾多，網絡規模龐大，三相數據均需進行分析，導致量測量劇增，大幅度提高了關鍵量測的辨識難度。配電網現有的關鍵量測辨識方法還難以滿足指標計算精度的要求。因此，如何準確辨識配電網關鍵量測量和關鍵量測組仍需進一步研究。

2 配電網可觀度提高技術

2.1 配電網量測技術概述

量測是狀態估計的重要數據來源，其數據的質量和冗余情況直接影響了系統狀態估計的可觀性與準確性。配電系統中，常見量測技術包括數據采集與監視控制系統SCADA（supervisory control and data acquisition）和高級量測系統AMI（advanced metering infrastructure），統稱為傳統量測技術。其中，SCADA應用更為廣泛，且成熟度較高，主要通過饋線終端單元FTU（feeder terminal unit）獲得網絡中支路功率、支路電流幅值和節點電壓幅值等數據。AMI量測相比于SCADA量測，還可采集配電網末端節點的注入功率量測。

目前，以同步相量測量單元PMU（phasor measurement unit）為代表的新型量測技術也逐漸用于配電網。相比傳統量測，PMU還可采集所在節點的電壓相量和所連支路的電流相量，同時具有高采樣率和能夠給數據提供精確時標的特性[18-19]。現有配電網常見量測體系如圖1所示。

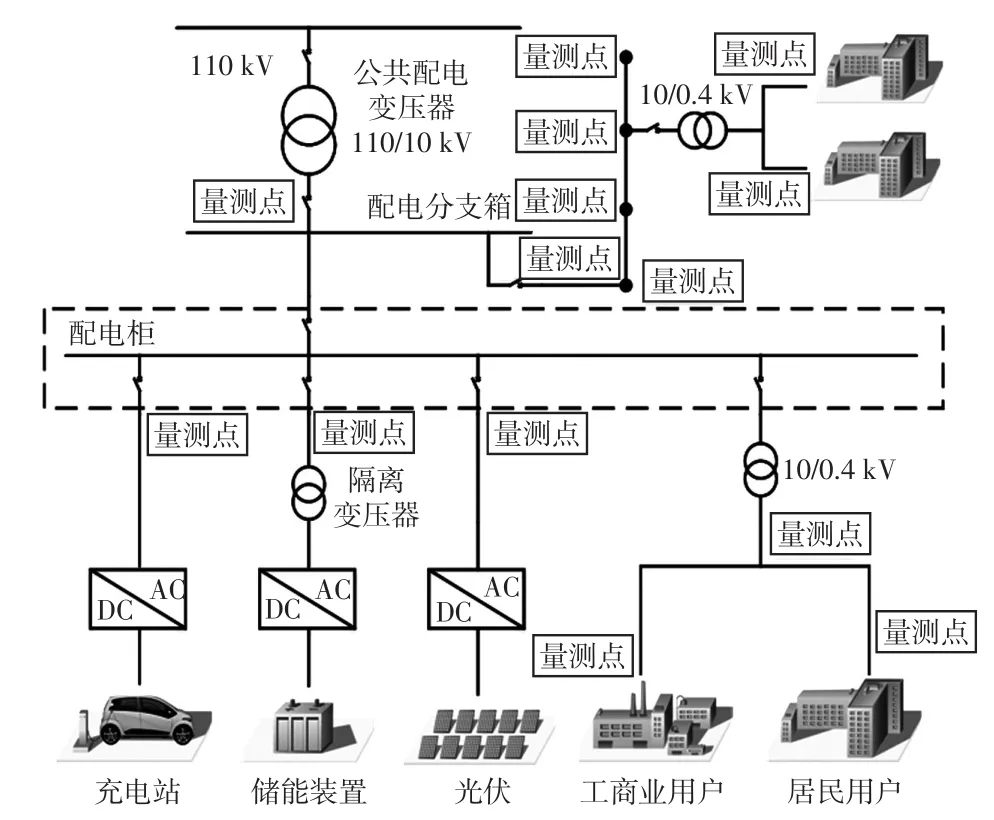
圖1 配電網常見量測體系Fig.1 Common measurement system of distribution network

隨著量測技術的發展，不僅使得可應用于狀態估計的數據量大為增加，同時也提高了數據的精確度，對配電網可觀度的提高起到了積極的推動作用[20]。但由于PMU量測裝置的成本較高，因此在未來較長時間內，配電網仍會保持PMU量測與傳統量測并存的局面。PMU可解決傳統量測的數據精度低和更新速度慢等困難，但其自身數據與傳統量測數據同步性較差，加大了時間坐標對齊的難度。因此，如何充分挖掘兩種量測系統的數據特點，研究精度較高的多源數據融合方法，對于提高配電網狀態估計可觀度具有重要意義。

2.2 量測配置的優化技術

隨著配電網智能化研究的逐步深入，數據種類與數量需求增多，對量測配置的要求也日益嚴格。在配電網中，量測配置過少會導致不可觀問題，狀態估計無法正常進行。量測配置過多又不符合配電網節點眾多、結構復雜的現狀。因此，優化量測配置、辨識網絡重要量測點對配電網狀態估計可觀度的提高具有重要作用。

2.2.1 滿足系統可觀度要求的優化配置模型

配電網量測配置優化評價指標以可觀性、估計結果精確度、數值穩定性、經濟性和可靠性等為主[21-23]。現有文獻多是基于多個評價指標展開優化，其中實現可觀性是必要條件。

研究發現，支路功率量測相較于其他量測對于配電網可觀度提高貢獻更大。因此，在傳統量測優化配置模型中，支路功率可觀理論獲得較多應用。該理論表明，若根節點U1已知，各支路的功率可測得，則其余各節點電壓可通過U1推導出，網絡完全可觀。現有FTU中“三遙”終端大多數可實現所在節點所有鄰接支路功率的量測。基于此，可建立基于支路功率可觀理論的配電終端優化模型[24]為

式中：yi表示節點i處是否安裝配電終端，yi={0 ,1}，y1=1，yi=0表示不安裝，yi=1表示安裝；An×b為節點支路關聯矩陣，An×b=[aij]n×b，n為節點數，b為支路數，若節點i與支路j相連，aij=1，否則aij=0；B1×b為支路可觀判定矩陣，B1×b=[b1j]1×b，若第j條支路兩端節點均為零注入節點，則b1j=0，否則b1j=1。

由第2.1節可知，傳統量測還可獲得節點電壓幅值、支路電流幅值和節點功率等量測數據。其中，由于現有配電網中AMI量測尚未普及，多數節點功率量測仍舊由誤差較大的偽量測代替。考慮到此類量測，在優化配置模型中可引入最大狀態量偏差的概念，若利用已有量測（包括實時量測和偽量測），通過狀態估計得到狀態變量的估計誤差均小于給定最大偏差，則系統可觀，且估計誤差越小，系統可觀度越高[25]。基于此，可完成對配電終端的配置優化。另外，為展現不同量測量的重要程度，文獻[26]利用廣義逆矩陣和最小二乘法唯一最小解的數學方法確定誤差表達式，對量測量重要性進行了排序，并結合經濟性與可觀度要求確定了最終的量測類型和安裝位置。

根據PMU量測特點可知，傳統量測的優化配置模型在PMU配置中同樣適用。然而，PMU短期內難以實現在配電網中全面鋪設[27]，且傳統優化配置模型無法充分利用PMU提供的相量數據，為優化量測配置問題的研究帶來新的挑戰[28]。

在電力網絡中，電壓相量可量測或可求出的節點為可觀節點，反之為不可觀節點。PMU優化配置OPP（optimal PMU placement）的研究多是以各節點完全可觀為約束條件。基于PMU量測的特性，常用的可觀性分析規則[29]如下。

（1）若某節點配置PMU，則其相鄰節點均可觀。

（2）若某可觀的零注入節點的相鄰節點中僅有1個節點可觀性未知，則該相鄰節點是可觀的。

（3）對于某可觀性未知的零注入節點，若其相鄰節點都可觀，則該零注入節點可觀；若相鄰節點中存在不可觀節點，則可利用節點方程來判斷該零注入節點是否可觀。

PMU最優配置的目標是保證滿足系統的可觀度和冗余度要求，確定PMU配置的最小數目np和最合適的位置S(np)。結合可觀性分析規則，可將此類問題[30]表述為

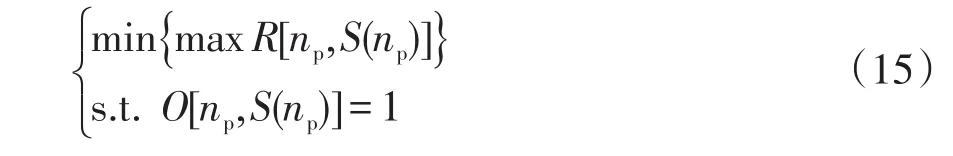
式中：R[np,S(np)]為量測冗余度指數；O為節點可觀性評估的邏輯函數。

考慮到PMU量測與傳統量測并存的現狀，可引入零注入節點和傳統量測提供的支路功率與節點功率實時量測數據來滿足式（15）約束條件的要求，并利用可觀性分析規則（2）和規則（3）來提升網絡可觀度[31-32]。另外，有學者提出簡化核心網可觀性原則，只在網絡樞紐部位裝設PMU，若能提供重點聯絡線的電壓及電流值，并能獲得重點線路的狀態軌跡變化情況和骨干網架的動態信息，即可認為該配置方式是合理的。

隨著多源數據融合技術的成熟，將會有更復雜的量測數據參與到狀態估計可觀性的研究中，對量測優化配置模型提出更高的要求。因此，開發更易求解、更好適應多源數據融合結果的優化配置模型，對于提高狀態估計可觀度具有重要意義。

2.2.2 優化配置模型的求解方法

由上文可知，求解配電網量測配置優化問題的目標是找出系統最佳量測點與量測類型，并配置合理數量的量測單元。傳統量測優化配置的求解過程與PMU類似，且PMU在配電網中已有較多的應用場景，因此本節只對OPP模型的求解方法展開論述。

OPP模型的求解方法主要分為確定性算法和啟發式算法兩大類。確定性算法以整數規劃為代表，包括整數線性規劃、整數二次規劃、0-1規劃法等，常用于解空間較小的場景，可以找到全局唯一最優解。啟發式算法以智能搜索為基礎，主要包括模擬退火法、禁忌搜索法、粒子群算法和遺傳算法等，適用于求解高維度、非線性、多目標模型，全局搜索能力強，但易陷入局部最優，常用次優解替代全局最優解。各種算法的優缺點如表1所示。

表1 OPP算法優缺點Tab.1 Advantages and disadvantages of OPP algorithm

在解決實際問題中，常常將不同的算法配合使用，充分發揮各自的優勢。例如，文獻[33]基于遺傳算法和模擬退火算法求解OPP問題，模擬退火算法用于降維搜索，遺傳算法用于全局優化，提升搜索能力的同時提高了搜索效率。

近年來，基于上述方法，許多學者結合配電網特性對OPP求解問題進行了更深入的研究。文獻[34]在充分考慮配電網輻射狀拓撲的基礎上，提出了等效縮小網絡規模的方法，并對各網絡分別進行OPP，滿足了系統可觀度要求并提高了優化速度。文獻[35]給出了一種基于負載特性的配電網絡壓縮方法，并結合自適應遺傳算法和禁忌搜索算法，使得PMU數量和系統冗余度同時達到最佳。文獻[32]考慮了配電網拓撲的多變性，提出一種定制遺傳算法，通過定制的交叉和變異，實現了多種拓撲結構平均可觀節點數目的最大化。也有文獻考慮到配電網中偽量測的存在，利用蒙特卡羅模擬方法配置PMU[36]。

OPP求解方法還有基于網絡拓撲結構的算法，主要包括最小生成樹和深度優先搜索法，計算速度快，可以更直觀地展現PMU配置過程，有助于對電網結構進行深入分析。例如，文獻[37]利用一種改進的圖論方法形成了包含網絡所有節點的最優生成樹，然后選擇PMU的關鍵安裝位置，實現網絡的完全可觀。文獻[38]提出一種基于圖論和層次分析法的多準則決策方法，該方法利用圖論的概念形成決策矩陣，應用層次分析法對優先級頂點進行排序，并考慮到零注入節點在OPP中的作用，滿足了在單PMU缺失或線路中斷情況下的網絡仍然可觀。但此類方法還存在著PMU配置數目較多，且配置方案單一的缺陷。

現有OPP求解方法大多用于解決可觀度和冗余度的優化問題，在處理可靠性、狀態估計精度等目標上效果不佳。因此在優化量測配置過程中，開發基于多目標函數的OPP求解方法仍是當前研究的重點內容。

2.3 偽量測建模與零注入節點處理

基于配電系統發展現狀，并考慮到部分地區經濟壓力與量測體系建設難度較大，一些配電網絡即使通過優化量測配置也難以滿足狀態估計可觀度要求。此時通過增加偽量測和虛擬零注入量測的方法可以實現在不增加量測設施情況下的可觀度的提高。常見的偽量測建模與零注入節點處理方法如圖2所示。

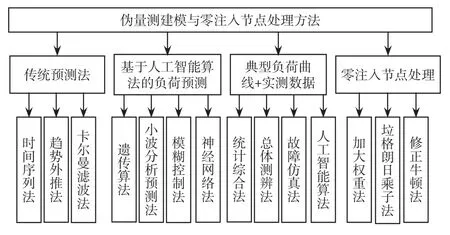
圖2 偽量測建模與零注入節點處理方法Fig.2 Method of pseudo-measurement modeling and zero injection node processing

2.3.1 偽量測建模方法

偽量測是指通過對歷史數據、實時量測數據、天氣情況等多方面因素的分析得到的未安裝量測設施區域的運行數據。與實時量測相比，偽量測具有較大的誤差，其誤差大小直接影響狀態估計可觀度，進而影響估計結果的精度，因此研究高精度偽量測建模方法具有重要意義。

現有配電網狀態估計偽量測多由短期負荷預測獲得。短期負荷預測方法主要分為傳統預測法和人工智能預測法[39]。傳統預測法是利用統計學知識，對歷史數據進行分析得到負荷偽量測，常見的方法有時間序列法、趨勢外推法、卡爾曼濾波法等。該類方法曾在很長一段時間可以滿足狀態估計偽量測精度的需求，但是隨著配電網規模的不斷擴大和用戶的持續擴增，簡單的基于統計學的分析方法已難以處理更加復雜的非線性負荷。基于人工智能算法的負荷預測為這些問題提供了很好的解決方法。遺傳算法、小波分析預測法、模糊控制法、神經網絡等已廣泛應用在基于短期負荷預測的偽量測建模中。例如，文獻[40]通過深度信念網絡DBN（deep belief network）算法進行配電網負荷預測，將多類型負荷的歷史數據及其對應日期類別、溫度作為訓練數據，選擇與當前負荷關聯性較強的數據作為DBN輸入，得到較高精度的偽量測。

上述方法均建立在歷史樣本數據之上，因而實時跟蹤電力系統狀態變化的能力較差。研究表明，基于歷史負荷曲線對當前時刻量測值進行曲線擬合獲取系統非線性函數的方法，可得到更加精確的未知節點負荷偽量測，同時可實時跟蹤系統變化。例如，文獻[41]將典型負荷曲線和從潮流模擬中得到的負荷數據用來訓練人工神經網絡ANN（artificial neural network），再將實際量測作為ANN的輸入，獲得了較高精度的節點注入功率偽量測。該方法將橫向實時量測數據與縱向歷史數據進行有效結合，并利用了ANN可以模擬人腦結構進行非線性映射的特點，使配電網狀態估計的計算精度達到較高水平，但是ANN的預測性能會隨著神經網絡層數的增加而降低。于是具有更強計算與適應能力的脈沖神經網絡被用于配電網偽量測建模[42]。

配電網中除功率數據外，其他類型數據同樣存在缺失情況。這些數據對于滿足可觀度要求、提高狀態估計精度同樣具有重要作用。對此，文獻[43]提出利用多元回歸的數學方法對配電網節點電壓數據進行建模，所得結果作為量測信息加入狀態估計器中，并利用算例驗證了所提建模方法的有效性，但該方法得到的電壓偽量測數據精度較低。因此，剖析配電網中負荷歷史數據與電壓、電流等非負荷歷史數據的關聯機理，探尋更適合于非負荷偽量測建模的方法將是狀態估計一個有意義的研究方向。

2.3.2 零注入節點處理方法

除了偽量測，實際配電網中還存在大量零注入節點。該類節點注入功率為0，不需要通過量測裝置獲取。若能將這些零注入節點功率作為量測量進行狀態估計，則可以大幅提高系統冗余度，滿足狀態估計可觀度要求。但是，在配電網狀態估計中，零注入節點功率的輸出結果有時難以保證嚴格為0，導致這些節點無法滿足潮流方程。因此，如何保證零注入節點輸出功率嚴格為0是計及零注入節點狀態估計研究中的重要問題。

在處理零注入節點時，一般采用加大權重法和拉格朗日乘子法兩種方法[44]。加大權重法是將零注入節點的注入功率視為精確度非常高的虛擬量測，給予其較大權重進行狀態估計計算。這種方法簡單方便、計算量小，但只能保證狀態估計結果中零注入節點的功率近似為0，同時還可能引起信息矩陣病態。在配電網中，R/X比值較大，引起信息矩陣病態的情況更為嚴重。拉格朗日乘子法是將零注入節點注入功率為0作為狀態估計目標函數的約束條件。該方法可以實現零注入約束的功率輸出嚴格為0，但該方法的信息矩陣不再正定，還需計算乘子協方差矩陣的對角元素，導致計算效率較低[45]。基于拉格朗日乘子法的缺點，文獻[40]受到基于修正牛頓法的零注入節點處理方法的啟發，將零注入約束轉化為線性約束，在一定程度上提升了計算效率[46-47]。

上文提到的零注入節點處理方法與現有配電網狀態估計算法還存在兼容性較差的缺陷，無法同時滿足計算速度與計算精度的要求。因此，如何使零注入節點處理方法更好地適應狀態估計算法仍是提高狀態估計可觀度與結果準確性的關鍵。

此外，隨著可再生能源發電技術的發展，多類型分布式電源DG（distributed generation）和電動汽車等設備規模化接入配電網，使得傳統配電網逐漸向具有控制能力的主動配電網發展。在主動配電網中，偽量測建模方法也將有所差異，主要體現在兩個方面：①DG并網機理與傳統電源有很大不同，若想實現全網可觀，則有必要基于并網機理對DG出力偽量測進行合理建模；②主動配電網功率不再是單向流動，電源和負荷擁有雙重不確定性，用戶具備生產者和消費者雙重身份，對偽量測建模具有較大影響[48]。因此需專門針對主動配電網的偽量測建模方法進行探討。

3 適用于主動配電網的偽量測建模技術

3.1 基于分布式電源并網機理的偽量測建模方法

主動配電網中傳統的負荷建模方法與第2.3.1節類似。對于主動配電網中DG的偽量測建模，一般將其作為有功功率-無功功率注入節點[49]。首先對DG的三相總出力進行預測，假設三相注入功率相等，進而得到單相功率注入偽量測，提高系統可觀度[50-51]。但該方法未考慮DG的不同并網機理，且未計及DG出力與配電網的三相不對稱性，導致偽量測精度較低。基于此，文獻[52]根據不同類型DG出力的特性，將DG并網節點類型分為有功及無功恒定的PQ節點、有功及電壓恒定的PV節點、有功及電流恒定的PI節點、有功恒定及無功受電壓限制的PQ（V）節點。通過對上述恒定物理量進行建模來可以提高含不同類型DG系統的偽量測精度。

另外，基于并網機理不同還可將DG分為直接并網（包括同步、異步風力發電機）和經脈寬調制PWM（pulse width modulation）換流器并網（包括光伏發電系統等）兩種類型。這兩種模型的等效電路分別如圖3和圖4所示。

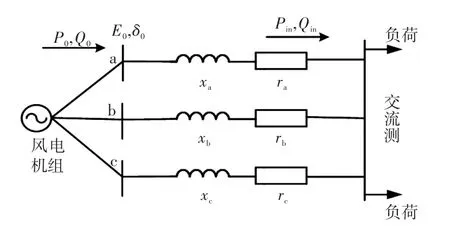
圖3 DG直接并網Fig.3 DG directly connected to grid

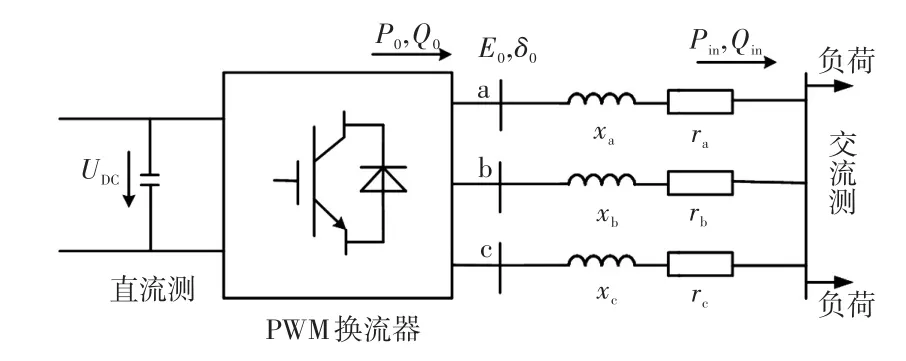
圖4 DG經PWM換流器并網Fig.4 DG connected to grid through PWM converter

這兩種并網模型中，直接并網風電機組與PWM換流器的端口電壓均呈三相對稱性，能夠用單相相量表示其三相電壓，在狀態估計過程中可將狀態變量擴展為

式中：˙為網側三相節點電壓狀態變量；E0和δ0分別為風電機組（或PWM換流器）端口的電壓幅值和相角。由此可見，基于并網機理的DG偽量測建模可更好適應配電網三相不對稱的特點。

在上述基礎上，文獻[53]提出在直接并網模型中，利用DG出力與功率因數得到的總有功功率與總無功功率可直接作為偽量測參與到狀態估計中。在經PWM換流器并網的模型中，根據控制策略的不同將偽量測模型分為

今后，將會有更多的DG并網方式出現，電力電子設備的應用類型也逐漸增多，DG可能會像同步機一樣參與電網調頻調壓，使得DG的偽量測建模更加困難，將會給狀態估計帶來更大的挑戰。因此，基于并網機理的分布式電源偽量測建模在配電網狀態估計可觀性研究中還有很大的潛力。

3.2 基于分布式電源與電動汽車不確定性的偽量測建模方法

在充分考慮主動配電網中分布式電源與電動汽車不確定性的情況下，現有偽量測精度提高方法主要有概率分布法[54-55]、模糊理論法[56]和區間數法[57]。概率分布法是根據大量歷史數據獲取分布式電源與負荷的概率分布，得到不確定變量的詳細先驗概率密度函數，進而獲得變量較為精確的偽量測值。文獻[54]在此基礎上利用高斯混合模型對DG出力偽量測概率密度函數進行表述，并用該函數方差替換最小二乘法狀態估計中原有的量測權重矩陣，取得了較好的估計效果。模糊理論法是通過建立不確定變量的隸屬度函數來表達相應偽量測。文獻[56]采用三角形隸屬度函數表示不確定測量值和參數的模糊數，提高了系統的可觀度，并得到了精度較高的狀態量估計值。

但由于DG出力與電動汽車充電過程的完整概率分布獲取難度較大，限制了以上兩種方法在主動配電網中的應用。相比于概率分布法與模糊理論法，利用區間數方法來獲得主動配電網中不確定變量偽量測問題無需建立參數具體的概率分布，只需知道其功率波動的上下界限即可，并且狀態估計結果可以提供更直觀的狀態變量上下界信息，故這種方法在主動配電網偽量測建模中的應用潛力巨大。文獻[58]建立了區間數的DG出力偽量測模型。對于風力發電，基于在線序貫-極限學習機的風電功率預測方法[59]，將輸出模式由單輸出轉化為雙輸出，進而得到風機出力偽量測的區間值。對于光伏發電，考慮到其出力區間受多因素影響，利用區間覆蓋率和區間寬度的綜合評估將多目標優化轉化為單目標優化[60]。所建立區間綜合評定函數為

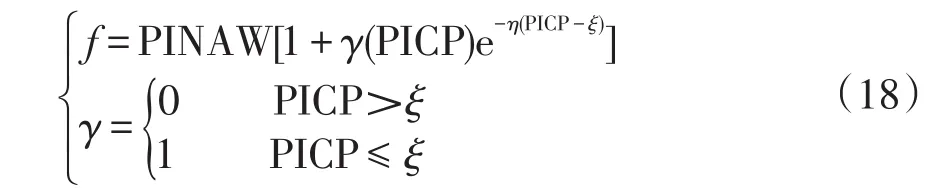
式中：PINAW為區間寬度；PICP為區間覆蓋率；γ為判定參量；ξ為置信度，也是f的調節參數；η為f的調節參數，一般取η∈[50,100]。將該優化函數代入到粒子群算法中可得到光伏出力偽量測的最優區間。

電動汽車充電過程具有強不確定性，難以從機理方向對其進行偽量測建模。因此，在利用區間數法對電動汽車不確定分析之前，應先通過一定數學方法找出歷史數據規律。基于此，文獻[57]采用基于統計數學的蒙特卡羅抽樣法與區間數法相結合的方式，對電動汽車充電過程中的負荷需求進行偽量測建模，文中首先利用蒙特卡羅方法對電動汽車1 d中各時間斷面總需求進行抽樣，并計算其期望值和標準差，然后用區間數對充電需求偽量測進行表述，即

式中：μEV為抽樣數據的期望值；σEV為抽樣數據的標準差；PEV(+)、PEV(-)分別為充電需求偽量測的最大值和最小值；υ為區間數的半徑調節參數，根據實際情況進行設定。隨著技術的發展，電網中出現了越來越多的儲能設備，電動汽車也可作為分布式電源向電網放電，加劇了主動配電網的不確定性。為滿足系統可觀度要求，對不確定性變量的偽量測建模方法提出了更高的要求。

4 結論與展望

本文結合近年來配電網狀態估計可觀性的研究情況，對配電網的可觀性分析方法、可觀性評價指標及可觀度提高方法進行了概述，重點歸納了適用于主動配電網的偽量測建模技術，并分別總結了現有方法存在的問題。根據目前智能配電網的發展，還有以下幾個方面需要進一步研究和改進。

（1）當配網拓撲發生變化時，系統的可觀度可能發生改變。尋找適用于多種拓撲環境的可觀度提高方案，使其更加契合配網拓撲因運行需要而多變的現狀，是當前研究有待解決的關鍵問題。

（2）現有配電網中模型驅動方法趨于成熟，數據驅動方法隨著人工智能的發展也日益成熟，兩種方法已廣泛應用于狀態估計可觀性研究的各個領域，但各有利弊。因此，考慮兩種方法的特性，將更多的數據模型聯合驅動模型用于可觀性分析方法和可觀度提高技術中值得研究。

（3）海量配網數據對狀態估計可觀性分析速度提出了更高的要求。現有的可觀性分析方法往往是將所有量測數據作為輸入，且未考慮誤差較大的不良數據。因此，運用關聯度分析模型剔除對系統可觀性影響較小的冗余變量，探尋適合可觀性分析的不良數據辨識算法，值得進一步研究。

（4）尋找更多可以提高數據分析準確度的數學統計方法，省去對蒙特卡羅算法的依賴，減小不確定性偽量測建模的誤差，也是目前值得研究的問題。