含運行協(xié)調性并改進差分進化算法的機組組合

張文軍，富立友

（上海電機學院商學院，上海 201306）

機組組合問題決定了發(fā)電機的啟停計劃及經(jīng)濟調度計劃，進而使系統(tǒng)在滿足電力需求的同時消耗最低的成本。近年來由于低成本和低排放，風力發(fā)電在世界各地得到迅速發(fā)展，然而風力發(fā)電具有間歇性且預測精度不高，這給風電并網(wǎng)后電力系統(tǒng)的安全穩(wěn)定運行帶來了巨大挑戰(zhàn)[1]。

為使電力系統(tǒng)在消納盡可能多風電的同時，兼顧經(jīng)濟性、清潔性，已有學者開展了一些研究。文獻[2]分析了不同目標組合策略下電力負荷、機組組合和優(yōu)化目標對風電消納的影響程度；文獻[3]借助非均分嚴格分段線性化方法，通過最小化弧長和弦長的平方差，完成二次煤耗成本函數(shù)嚴格線性化，實現(xiàn)了火電機組調峰煤耗特性的精確模擬；文獻[4]兼顧發(fā)電側與需求側柔性負荷的雙側協(xié)調配合，建立了考慮柔性負荷的多目標安全約束機組組合優(yōu)化模型；文獻[5]建立了風電光伏水電火電聯(lián)合優(yōu)化調度模型，提出通過多種能源聯(lián)合運行及與儲能裝置協(xié)調配合的調度方法，減少可再生能源棄電率。現(xiàn)有研究主要側重電力系統(tǒng)機組組合中經(jīng)濟性、節(jié)能性、清潔性及求解算法的優(yōu)化，未能針對低碳轉型背景下電力系統(tǒng)運行時線路的協(xié)調穩(wěn)定性開展專題分析與深入研究。

在大、小機組分布不均且負荷較重的系統(tǒng)內，傳統(tǒng)調度模式下排放量小、煤耗低的大機組出力會增加，而排放量大、煤耗高的小機組出力會減少，此調度模式會導致部分線路重載甚至過載運行，增加系統(tǒng)的運行風險[6]。因此，機組組合的優(yōu)化需考慮運行協(xié)調性，即需要降低系統(tǒng)運行過程中支路的高負載率。

在機組組合優(yōu)化問題中，多目標差分進化算法DEAMO（differential evolution algorithm for multi-objective）為模型的求解開拓了新視野。DEAMO是一種基于群體智能的多目標啟發(fā)式優(yōu)化算法，其利用種群個體之間的差異性引導算法在解空間中進行搜索，具有全局搜索能力和種群多樣性的特點[7]。目前，多種DEAMO的變體[8-12]被用于機組組合問題的求解并取得了不錯的優(yōu)化效果。

綜上，本文建立含系統(tǒng)運行協(xié)調性、清潔性、節(jié)能性、經(jīng)濟性的4目標優(yōu)化模型，并提出含動態(tài)搜索空間的混沌多目標差分進化CMODE/DSS（chaos multi-objective differential evolution with dynamic search space）算法求解模型，分析不同調度方案下線路運行的穩(wěn)定性能，從而驗證所提優(yōu)化模型在運行調度時可提高系統(tǒng)安全運行水平。

1 建模過程

1.1 目標函數(shù)

考慮系統(tǒng)運行協(xié)調性、清潔性、節(jié)能性、經(jīng)濟性的含風電場機組組合問題的主要目標是在滿足系統(tǒng)安全約束和機組自身運行約束下，決定何時開啟和關閉火電機組來達到最小化運行耗量、盡可能地減少棄風量、最大限度地減少二氧化碳的排放及降低運行支路的高負載率。對于常規(guī)火電機組，煤耗成本及二氧化碳排放量可表示為發(fā)電功率的二次函數(shù)形式，目標函數(shù)分別為

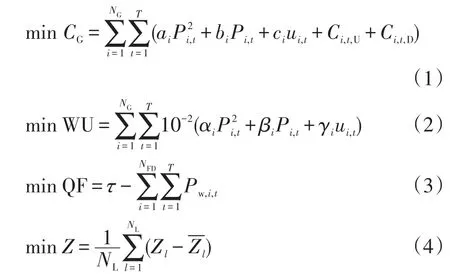
式中：CG為火電機組煤耗成本，＄；NG為火電機組數(shù)；T為機組運行總時間段數(shù)，h；ai、bi、ci分別為火電機組i的煤耗系數(shù)；Ci,t,U、Ci,t,D分別為火電機組i在t時刻的開、停機費用，＄/次；WU為火電機組二氧化碳排放量，t；αi、βi、γi分別為火電機組i的二氧化碳排放量系數(shù)；QF為棄風量，MW；τ為1個較大的常數(shù)，本文取1 600；ui,t為火電機組i在t時段的運行狀態(tài)，機組運行為1，機組停運為0；Pi,t、Pw,i,t分別為火電機組i、風電機組i在t時段的有功出力，MW；NFD為風電機組數(shù)；Z為線路運行協(xié)調性；NL為運行支路總數(shù)；Zl、-Zl分別為支路l在運行時段內的負載率、平均負載率，Z越小表示各支路功率分布越均勻且運行協(xié)調性越好。

1.2 約束條件

1.3 多目標優(yōu)化模型的數(shù)學描述

多目標優(yōu)化模型可表示為

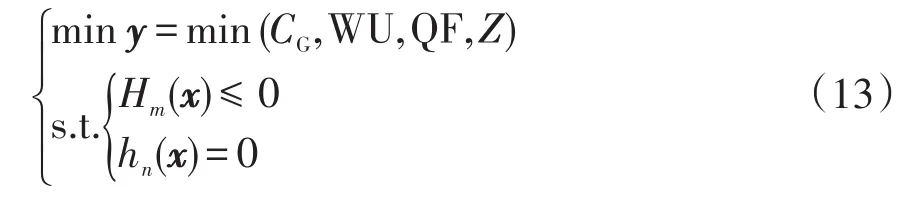
式中：yy為目標函數(shù)向量；xx為火電機組、風電機組的運行狀態(tài)和出力構成的決策向量；Hm(x)≤0定義了m個不等式約束；hn(x)=0定義了n個等式約束。

2 CMODE/DSS算法

隨著多目標優(yōu)化模型的目標函數(shù)數(shù)量的增加，折衷變得復雜且難以量化，需要使用帕累托最優(yōu)概念來描述目標[13-16]。文獻[17]在多目標進化算法EAMO（evolution algorithm for multi-objective）的基礎上引入動態(tài)搜索空間，發(fā)展成了一種基于動態(tài)搜索空間的多目標進化算法SSMOEA（search space-based multi-objective evolutionary algorithm），引入差分進化算子[18]后關鍵操作如下。

2.1 變異與交叉

2.2 生成動態(tài)搜索空間

2.3 選擇

為了使種群個體向著最優(yōu)目標進化并且能夠獲得帕累托前沿面分布均勻的個體，個體的適應度計算應包含收斂性和多樣性方面的信息[19]。本文考慮了3個基于動態(tài)搜索空間的標準來計算個體q的適應度并進行快速非支配排序[20]，3個標準分別為搜索空間等級GR、搜索空間擁擠距離GCD、搜索空間點距GCPD。GR和GCD的表達式分別為

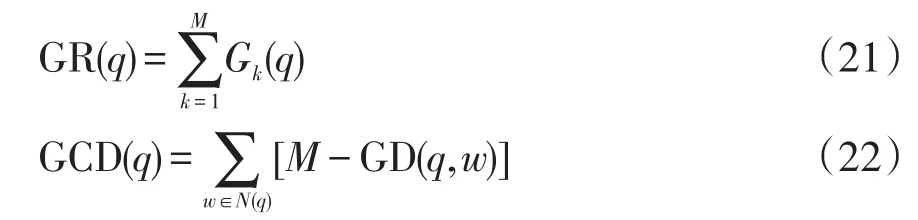
式中，N（q）表示q的鄰集。GR和GCD在個體的收斂性和多樣性方面提供度量，由于計算基于個體的超框坐標且都為整數(shù)，可能無法完全區(qū)分所有個體。因此提出以個體q與其所處超框頂點的歸一化歐式距離作為適應度比較的補充，即搜索空間點距GCPD。GCPD主要評估個體的收斂性，其表達式為

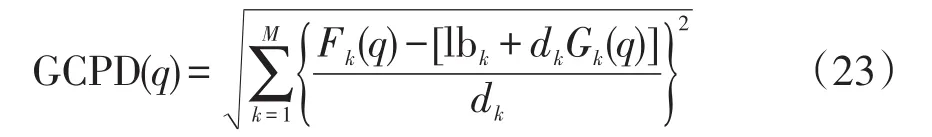
2.4 改進Tent映射的混沌種群初始化及參數(shù)K、RF的動態(tài)調整

初始種群直接影響進化算法的收斂速度和尋優(yōu)精度，隨機初始化種群無法確保種群在搜索空間中均勻分布[21]，將混沌序列和進化算法融合可使初始種群具有更好的多樣性，避免陷入局部最優(yōu)[22]。混沌序列的生成方式有多種，其中Tent映射生成序列均勻性更好[23]，然而Tent映射生成的混沌序列存在小周期和不確定周期點的不足。文獻[24]在傳統(tǒng)Tent映射中添加隨機變量加以改善，其數(shù)學表達式為

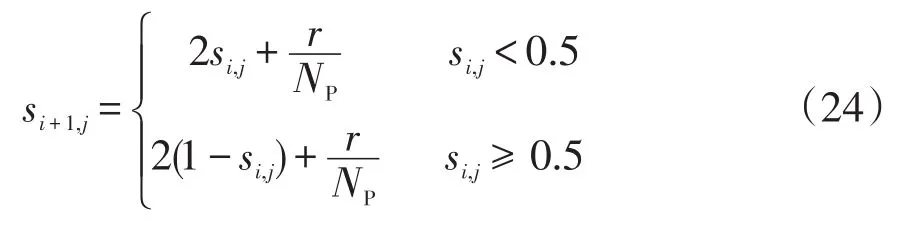
式中：si,j為生成初始種群前混沌矩陣中的元素；s1,1,s1,2,…,s1,D為D個0-1之間的隨機數(shù)；i=1,2,…,NP；j=1,2,…,D；r為0-1之間的隨機數(shù)；NP為種群規(guī)模。混沌序列逆映射數(shù)學表達式為

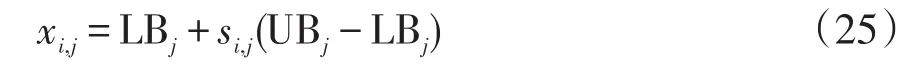
式中，UBj、LBj分別為決策變量xi,j的上限、下限。改進Tent映射的混沌種群初始化步驟如下。

步驟1隨機生成D個0-1之間的隨機數(shù)，形成初始序列s1=(s1,1,s1,2,…,s1,D)。

步驟2根據(jù)式（24）生成混沌矩陣S為

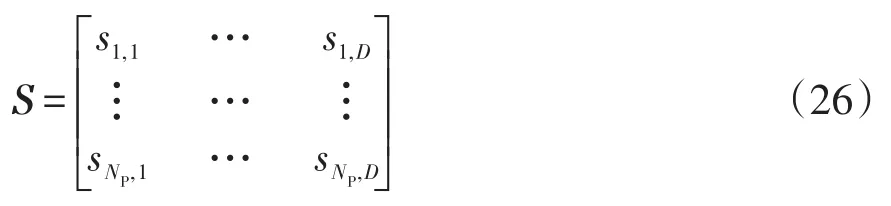
步驟3利用式（25）將式（26）混沌矩陣中的元素逆映射，得到初始種群。

式（14）和式（15）中K和RF的初始值取0-1之間的隨機數(shù)，之后的迭代過程采用式（24）進行動態(tài)調整。

2.5 算法流程

在得到帕累托前沿后，為分析本文所提模型在優(yōu)化支路穩(wěn)定性能方面的效果，采用優(yōu)劣解距離法TOPSIS（technique for order preference by similarity to an ideal solution）[25]求取調和解。

采用CMODE/DSS算法求解模型的流程如圖1所示。

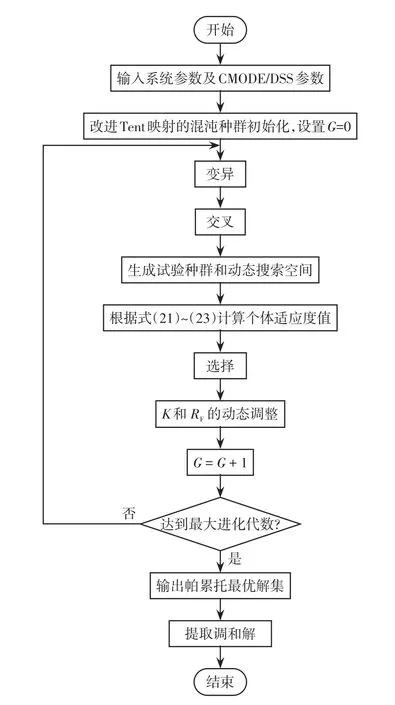
圖1 CMODE/DSS算法流程Fig.1 Flow chart of CMODE/DSS algorithm

3 算例分析

反向世代距離IGD（inverted generational distance）不僅可以評價EAMO的收斂性，還可以評價帕累托前沿中個體的均勻分布性，IGD值越小說明算法得到的帕累托前沿收斂性越好、分布越均勻[19]。為測試CMODE/DSS的整體性能，在Matlab平臺采用IGD與6種EAMO，即多目標帕累托采樣算法 MSOPS（multiple single objective Pareto sampling）[26]、基于 ?支配的多目標進化算法 ?-MOEA（epsilon-domination based multi-objective evolutionary algorithm）[27]、基于分解的多目標進化算法MOEA/D（multi-objective evolutionary algorithm based on decomposition）[28]、基于網(wǎng)格的進化算法GrEA（grid-based evolutionary algorithm）[29]、基于超體積估計的快速多目標優(yōu)化算法HypE（fast hypervolumebased many-objective optimization）[30]、基于偏好排序的多目標進化算法POGA（preference ordering based genetic algorithm）[31]。在M=4的多目標測試函數(shù)DTLZ1（Deb Thiele Laumanns Zitzler/1）[32]、DTLZ2上進行比較，種群規(guī)模為50，最大迭代次數(shù)為100 000，6種EAMO的結果取自文獻[26-31]，比較結果如表1所示。

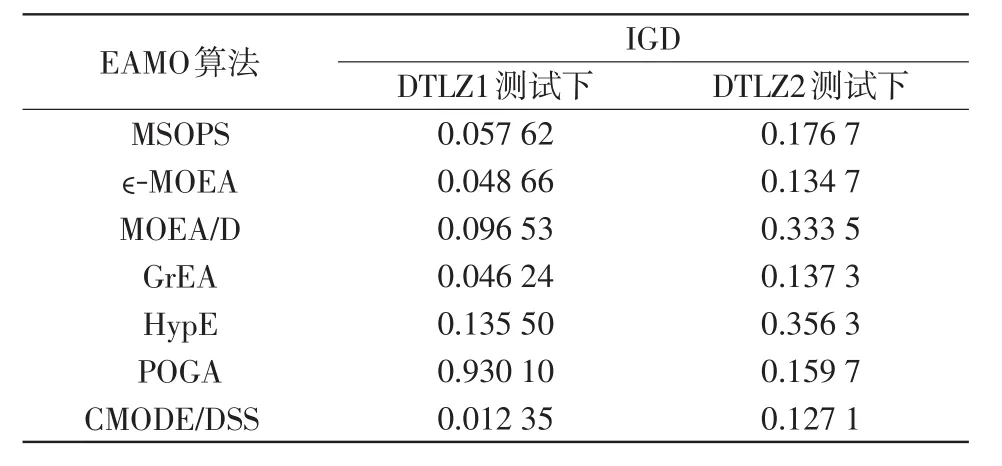
表1 CMODE/DSS 與6種EAMO在DTLZ1、DTLZ2中的IGD比較Tab.1 Comparison of IGD among CMODE/DSS and six kinds of EAMO in DTLZ1 and DTLZ2

由表1計算結果可知，相比于其他6種EAMO，CMODE/DSS的IGD值最小，說明CMODE/DSS搜索到的帕累托最優(yōu)解集在目標空間中的分布較為均勻且收斂性較好。

以IEEE 30節(jié)點系統(tǒng)為算例，系統(tǒng)如圖2所示，系統(tǒng)含有1個風電場（位于20節(jié)點）、6臺火電機組（分別位于1、2、5、8、11、13節(jié)點）、41條支路。機組和系統(tǒng)參數(shù)參照文獻[33]，如表2～4所示。風電場數(shù)據(jù)參照文獻[34]，風電預測出力如圖3所示。

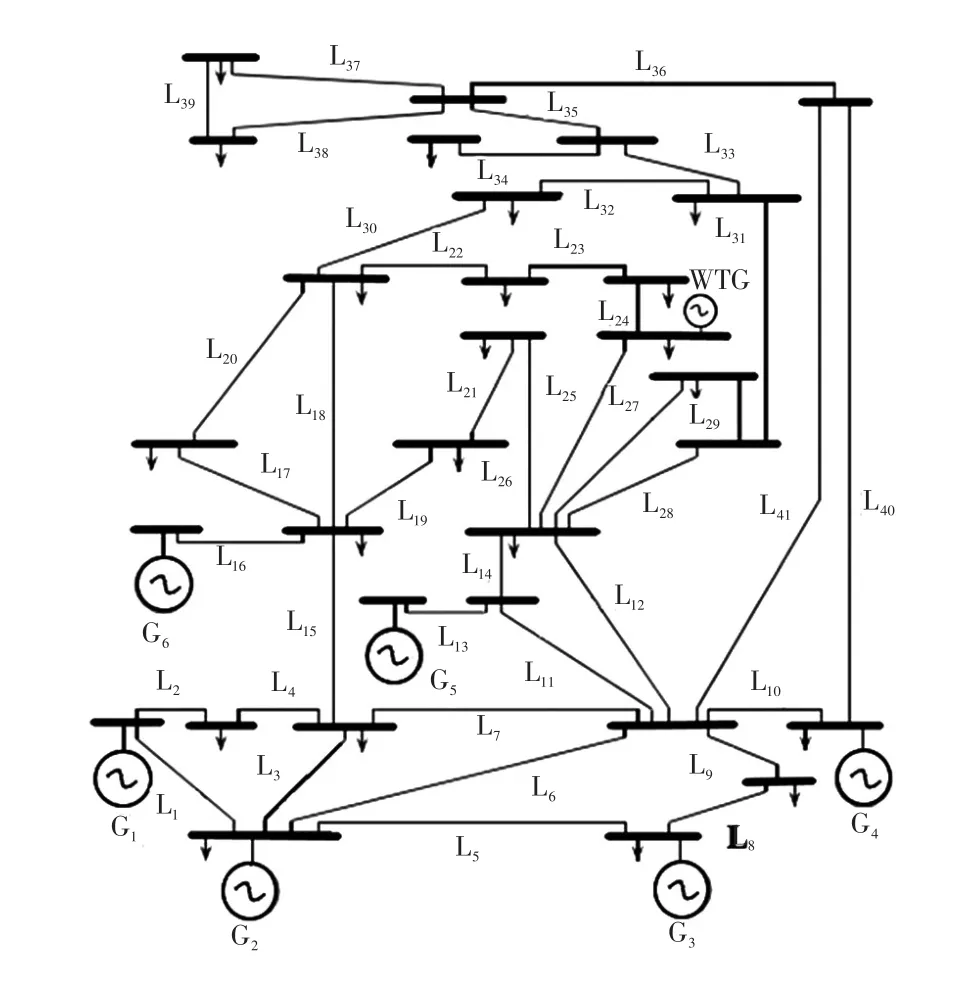
圖2 IEEE 30節(jié)點系統(tǒng)Fig.2 IEEE 30-node system

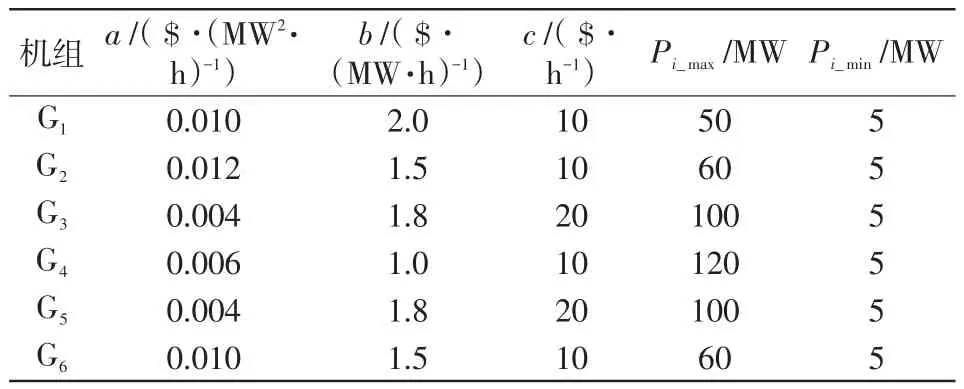
表2 機組煤耗系數(shù)及出力限制Tab.2 Unit coal consumption coefficient and output limit

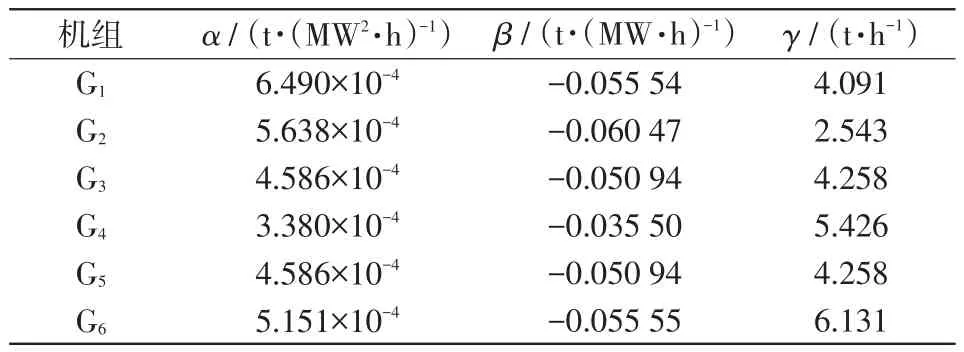
表3 機組二氧化碳排放量系數(shù)Tab.3 Unit carbon dioxide emission coefficient

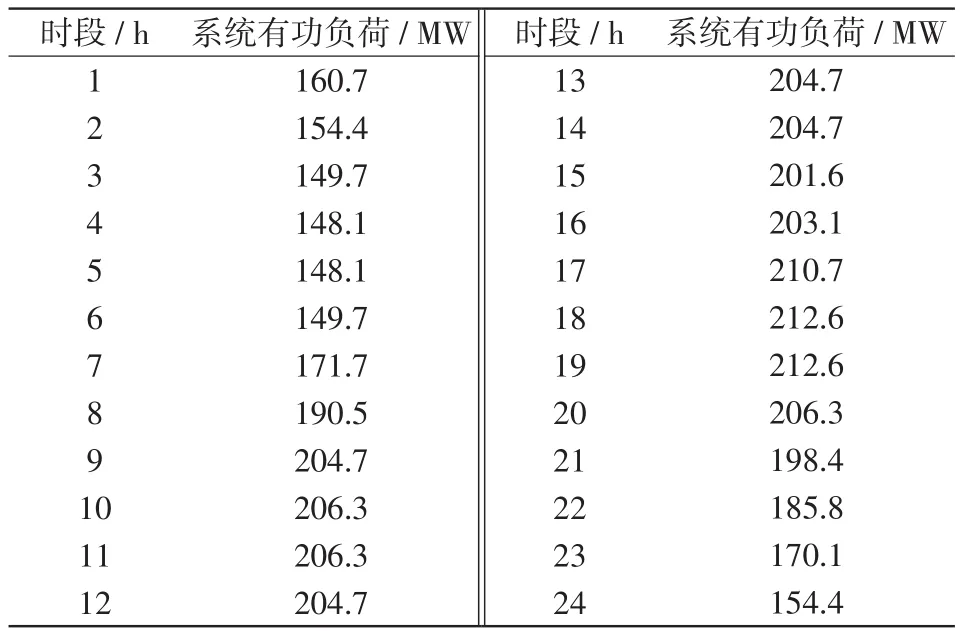
表4 系統(tǒng)有功負荷Tab.4 System active load

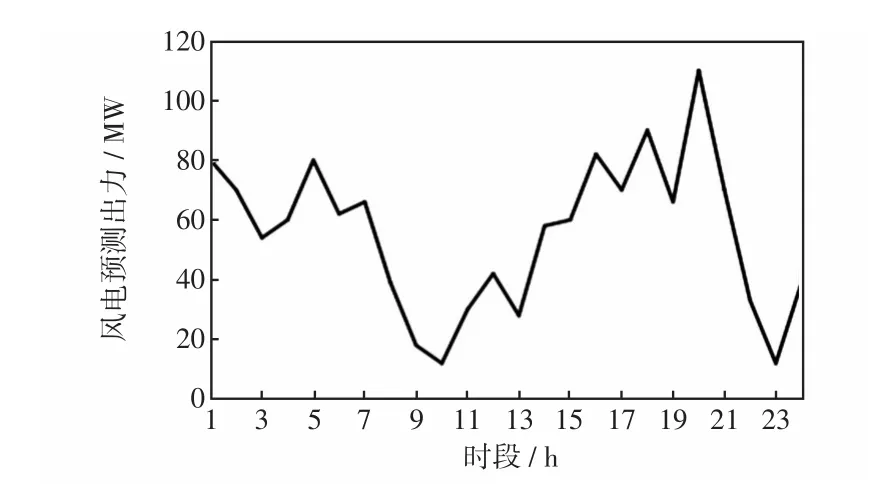
圖3 風電預測出力Fig.3 Forecasted wind power output

CMODE/DSS求解模型得到的帕累托前沿如圖4所示，目標函數(shù)Z線性映射到圖4中圓圈的體積，圓圈體積越小表示Z越小。

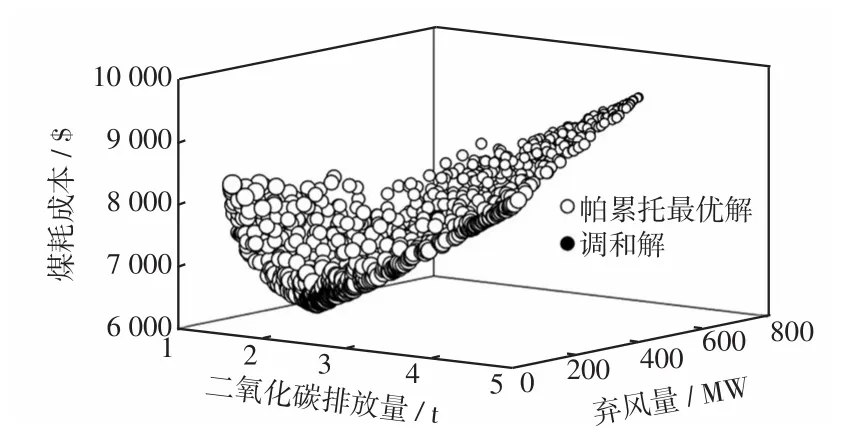
圖4 4目標帕累托前沿Fig.4 Four-goal Pareto frontier

從圖4可以看出，Z總體上隨煤耗成本的增加而降低，隨棄風量的增加而降低，隨二氧化碳排放量的增加而先增加后降低。綜合考慮4個目標時，風電并網(wǎng)減少了火電機組所需出力，因此棄風量的減少帶來煤耗成本的降低，然而風電在系統(tǒng)各運行時段的出力隨機性導致支路潮流分布不均，個別支路長時間運行在高負載率下，致使系統(tǒng)協(xié)調性指標Z變大。同時系統(tǒng)內各火電機組二氧化碳排放系數(shù)和煤耗系數(shù)存在差異，若盡可能調用二氧化碳排放少的機組會無法兼顧經(jīng)濟性與協(xié)調性，導致煤耗成本及Z的增加。

定義目標函數(shù)為最小化煤耗成本、棄風量、二氧化碳排放量的3目標調度模型為模型1；目標函數(shù)為最小化煤耗成本、棄風量、二氧化碳排放量、運行協(xié)調性的4目標調度模型為模型2。

模型1調和解中重載支路的負載率及模型2優(yōu)化后的支路負載率如圖5和圖6所示。

圖5 支路10的負載率Fig.5 Load rate of Branch 10

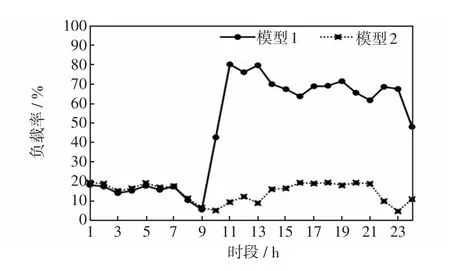
圖6 支路21的負載率Fig.6 Load rate of Branch 21

從圖5和圖6可以看出，模型1下支路10在24個時段內均滿載，支路21在時段11的負載率高達80.2%；模型2優(yōu)化后，41條支路在24個時段內無滿載、重載狀態(tài)，支路負載率最高為64.4%，支路10在24個時段內的負載率均降低至65%以下，支路21在時段11的負載率降低至9.4%。盡管模型1受支路安全約束的影響沒有過載運行，但有支路長時間處于滿載狀態(tài)，不利于系統(tǒng)安全穩(wěn)定。模型2考慮了函數(shù)Z的影響，滿載、重載程度得到了有效緩解。

使用兩種模型調度方案，進一步研究預想故障對系統(tǒng)安全運行的影響，并且在不導致系統(tǒng)解列的前提下開斷高負載率的支路10。采用表征支路功率越限嚴重程度的性能指標PIP作為評價指標[35、36]，其表達式為

式中，δL為運行時段內過負荷支路集合。

開斷支路10后，模型1調和解中超載支路的負載率及模型2優(yōu)化后的支路負載率如圖7和圖8所示。

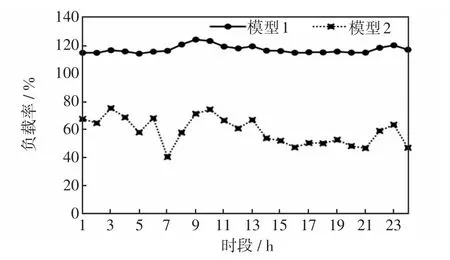
圖7 支路40的負載率Fig.7 Load rate of Branch 40

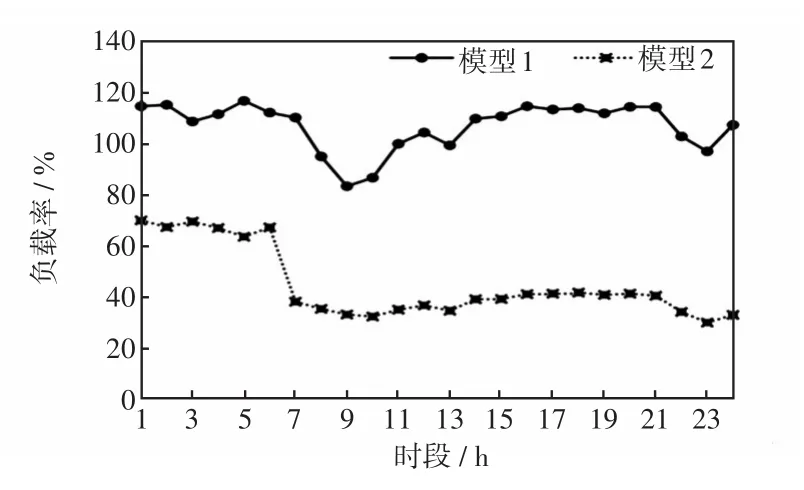
圖8 支路41的負載率Fig.8 Load rate of Branch 41

從圖7和圖8可以看出，開斷支路10后，模型1下支路40在運行時段內均超載，支路41在運行時段內或超載、或重載運行，預想故障下的系統(tǒng)處于緊急狀態(tài)，原系統(tǒng)運行在不安全狀態(tài)；模型2優(yōu)化后，預想故障下所有支路在運行時段內無超載、滿載，支路負載率最高為75.5%，預想故障下的系統(tǒng)處于安全正常運行狀態(tài)，原系統(tǒng)運行在安全正常狀態(tài)。

為便于比較分析，計算出了模型1調和解的Z值，模型1和模型2調和解的目標函數(shù)值對比結果及開斷支路10后的性能指標PIP如表5所示。

表5 不同模型下調和解的各目標函數(shù)值Tab.5 Value of each objective function in the harmonic solution under different models

從表5可以看出，模型2的煤耗費用略微增加（18＄/h），二氧化碳排放量與棄風量基本維持不變，系統(tǒng)Z值由1.903下降為0.771；模型1在預想故障下出現(xiàn)了不同程度的支路過載且PIP值較大，模型2的PIP值為0，在預想故障下各支路均未出現(xiàn)過載，表明各支路功率分布更為均勻，支路運行的安全性能提高。由此說明，模型2的優(yōu)化需要犧牲一定的經(jīng)濟利益，但是會極大地提高系統(tǒng)安全穩(wěn)定、協(xié)調運行的水平。

4 結論

本文針對傳統(tǒng)調度策略導致部分支路運行重載甚至過載的問題，構建了同時考慮經(jīng)濟性、節(jié)能性、清潔性和運行協(xié)調性的多目標機組組合優(yōu)化模型，提出了一種CMODE/DSS算法，得到以下結論。

（1）從支路潮流均勻分布的角度提出系統(tǒng)運行的協(xié)調性指標，在此基礎上構建的綜合考慮系統(tǒng)運行經(jīng)濟節(jié)能、清潔環(huán)保、安全穩(wěn)定的調度模型將調度運行中滿載支路的負載率由100%降低至65%以下，將預想故障中超載支路的負載率由120%降低至80%以下，PIP由49.3降低至0，有效提高了系統(tǒng)運行的安全性。

（2）CMODE/DSS算法在差分進化的尋優(yōu)機制中構建動態(tài)搜索空間，以及采用改進Tent映射的混沌種群初始化和變異、交叉概率的動態(tài)調整策略，提高了算法的收斂性與帕累托前沿個體的均勻分布性，提高了進化算法的全局搜索能力。