基于移相變壓器的直驅風機次同步振蕩抑制

韓平平，王 希，王 歡，李曉明

（1.新能源利用與節能安徽省重點實驗室（合肥工業大學），合肥 230009；2.國網河北省電力有限公司電力科學研究院，石家莊 050021）

隨著多種新能源發電并網、電力電子元件覆蓋電力系統的各個環節，電網強度逐漸被削弱[1]，增大了直驅風機PMSG（permanent magnet synchronous generator）并網引起次同步振蕩SSO（subsynchronous oscillation）的風險。2015年，我國新疆某直驅風電場向附近無串補交流電網供電時，引發了持續的SSO現象[2-3]，導致數百公里外的火電廠汽輪機組因扭振保護動作而發生嚴重的切機事故，危害了區域電網的穩定性。因此，為了保證PMSG并網系統穩定性，亟需開展PMSG接入弱交流電網的SSO發生機理及其抑制方法研究。

國內外針對PSMG的SSO發生機理開展了一些研究[4-6]。文獻[4]基于頻率掃描法推導得出PMSG在次同步頻率范圍內產生負電阻和容性電抗效應，其與弱電網中的電感構成二階諧振電路，導致發散的SSO，從而揭示了PMSG與弱交流電網交互作用引發SSO的機理。文獻[5]研究了基于PMSG并網系統的閉環互聯模型，PMSG網側換流器GSC（gridside converter）與同步機及不同PMSG的GSC間會發生開環模式諧振，引發系統次/超同步振蕩。文獻[6]推導了GSC對電網諧波擾動的響應過程，當換流器的輸入輸出諧波間相位滿足一定關系時，輸出諧波不斷被放大，導致次/超同步振蕩的產生。

針對PSMG并網引起的SSO問題，目前主要有以下兩類抑制措施：①優化換流器控制系數或者改善控制環結構[7-8]，雖然這類方法可以抑制SSO，但無法保證風機換流器的最優控制目標；②通過引入阻尼控制環節或者引入虛擬電阻環節增大系統阻尼，達到抑制SSO的目的[9-10]，然而這類方法涉及的控制環節較多，在工程實際中會受到控制器硬件的限制，此外，這類方法是針對特定頻率的SSO設計，但由于電網實際運行情況復雜多變，振蕩頻率并非恒定不變[11-12]。因此，提出一種考慮多工況和頻率多樣性的SSO抑制方法對于提升PMSG并網系統穩定性具有重要的現實意義。

移相變壓器PST（phase shifting transformer）通過對各繞組的有效組合，能夠同時調節輸出電壓的幅值和相位[13]。在PMSG并網系統中加入PST，會影響PMSG和弱電網的交互作用，進而改變PMSG接入弱交流電網的SSO特性。目前，國內對PST的研究及工程應用相對較少，且主要用于實現潮流控制和在線融冰[14-15]，尚無抑制SSO方面的研究。本文提出利用PST抑制PMSG接入弱交流電網SSO的方法。一方面，PST能夠在系統工況改變時，無區別地抑制頻率變化的SSO；另一方面，PST投建成本較低、經濟性高，具有良好的應用前景。

本文針對現有文獻中PMSG的SSO研究存在的不足，首先建立了PMSG接入弱交流電網的小信號模型，通過模態與參與因子分析揭示了SSO的發生機理；然后，提出了一種基于PST的SSO抑制方法，能夠在多工況下抑制SSO的發生，而不需要對GSC的控制結構或控制參數有任何改動；最后，在Matlab/Simulink上搭建了基于PST的PMSG并網系統仿真模型，通過測量系統等值阻抗驗證了PST抑制方法的合理性，通過仿真波形及其頻譜圖驗證了PST對SSO的抑制效果。

1 PMSG并網系統動態模型

1.1 PMSG并網系統數學模型

PMSG并網系統主要由機械部分、背靠背換流器、鎖相環PLL（phase locked loop）、直流側電容器及輸電線路構成，系統主電路拓撲如圖1所示，其中Cdc為直流側電容；Lg為風機網側濾波電感；L1、R1、C1分別為輸電線路電感、電阻和對地電容；大電網電壓等級為110 kV。背靠背換流器由機側換流器MSC（machine-side converter）和GSC兩部分組成，控制系統框圖如圖2所示。

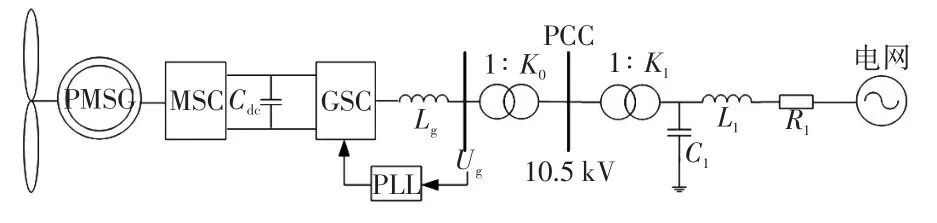
圖1 PSMG并網系統主電路拓撲Fig.1 Main circuit topology of grid-connected PMSG system

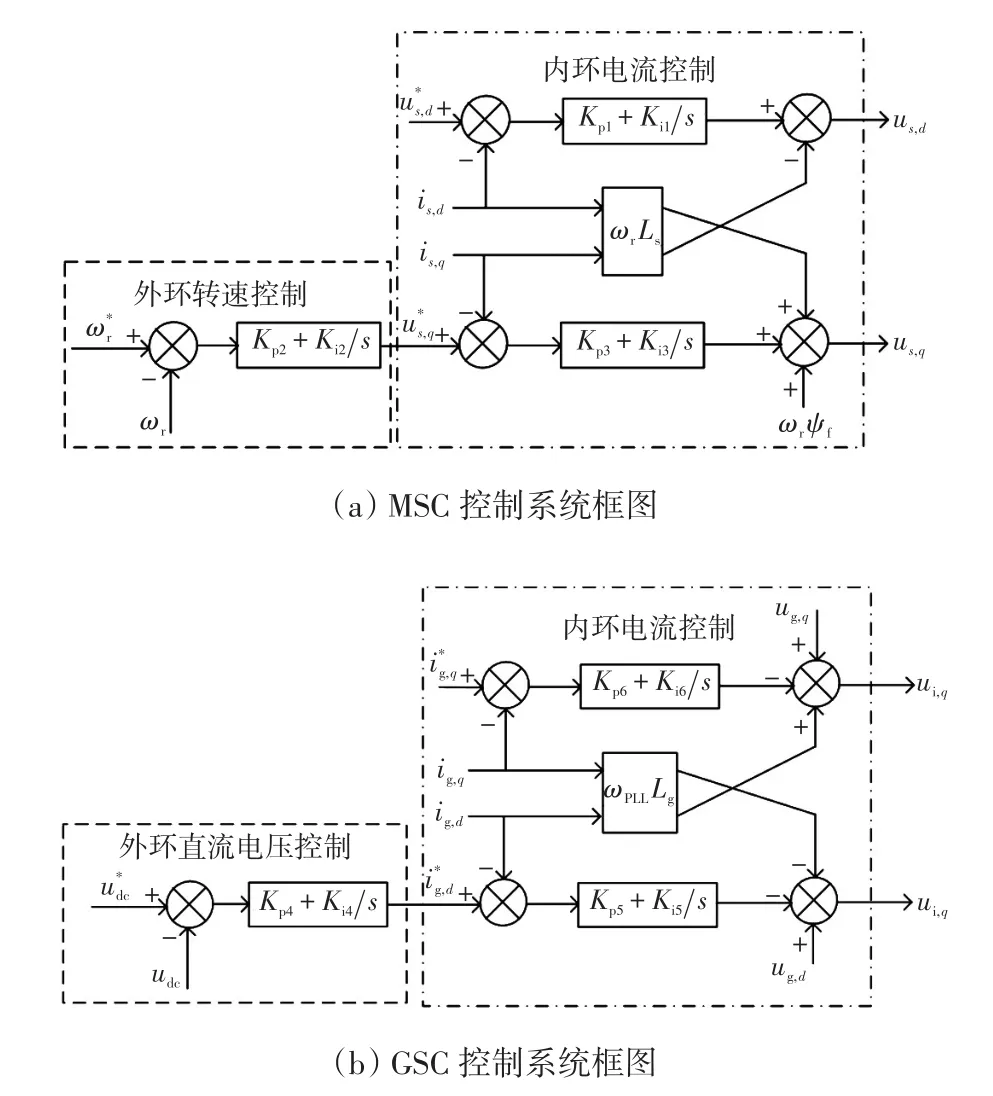
圖2 背靠背換流器控制系統框圖Fig.2 Block diagram of control system of back-to-back converter

1.2 PSMG并網系統小信號模型

根據上述PSMG并網系統數學模型，聯立推導出單臺PSMG并入弱交流電網的全系統數學模型，經線性化可建立全系統的小信號模型。全系統數學模型由18個微分方程和7個代數方程組成，可以表示為

選取1個平衡點，在此平衡點處進行泰勒展開，計算出各變量的初始值，將其代入式（9）中的微分-代數方程組，從而建立系統的小信號模型，即

式中：Δx、Δu分別為線性化后的狀態變量和輸入變量；A、B分別為小信號模型的狀態矩陣和代數矩陣；x為狀態變量，x=[ωt，x1，x2，x3，is,d，is,q，xPLL，θPLL，x4，x5，x6，ig,d，ig,q，udc，ug,d，ug,q，il,d，il,q]。

2 SSO機理分析

根據上述小信號模型，利用特征值分析法得到PSMG接入弱交流電網的主要振蕩模態[16]，并對其中SSO模態進行歸一化參與因子計算，揭示SSO的發生機理。

電網強弱用短路比SCR（short circuit ratio）表示，定義2＜SCR＜10時為弱電網。按照表1參數開展小信號建模及分析，設定平衡點vw=11 m/s，計算出各變量相應的初始值。假設SCR=2.0，構造弱電網環境。基于特征值分析法計算單臺PSMG接入弱交流電網的主要振蕩模態，計算結果如表2所示。

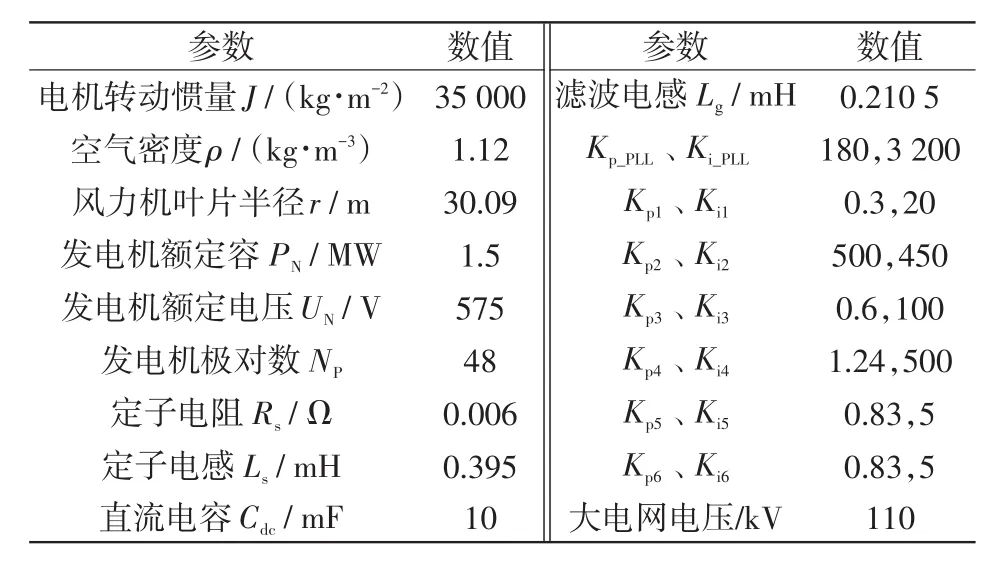
表1 PSMG并網系統參數Tab.1 Parameters of grid-connected PMSG system

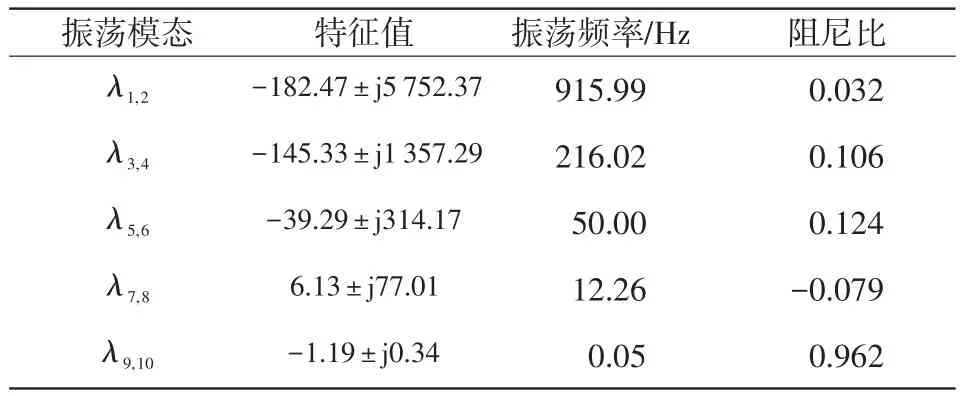
表2 PSMG接入弱交流電網的振蕩模態Tab.2 Oscillation modes of PMSG connected to weak AC power grid

由表2可知，在弱電網環境下，PSMG并網系統中存在5個振蕩模態，分別為2個中高頻振蕩模（態λ1,2、λ3,4）、1個工頻振蕩模態（λ5,6）、1個SSO模態（λ7,8）和1個低頻振蕩模態（λ9,10）。其中，SSO模態特征值實部為正，表現為負阻尼，在系統參數整定不恰當時易發生SSO，會影響系統的穩定性；其他4個振蕩模態的特征值實部均為負值，表現為正阻尼，不會影響系統的穩定運行。因此，本文將圍繞SSO模態展開研究。

對SSO模態λ7,8進行歸一化參與因子計算，計算結果如圖3所示。可以看出，SSO模態受狀態變量ig,d、ig,q、ug,d、ug,q的影響程度大。同時，由前述小信號模型的動態方程可知，ig,d、ig,q主要與GSC控制環節相關，ug,d、ug,q主要與輸電線路相關，這表明PSMG接入弱交流電網的SSO由GSC與弱交流電網的交互作用引發。

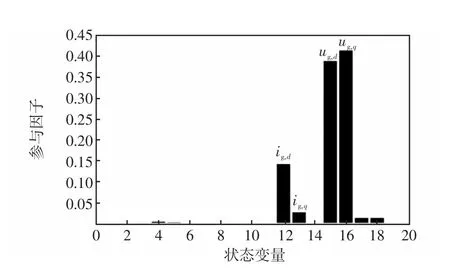
圖3 SSO的歸一化參與因子Fig.3 Normalized participation factors of SSO

3 PST基本原理及SSO抑制方法

由機械開關通過切換變壓器分接頭實現的PST在歐美電網中己有較為廣泛的應用[17-18]，然而由于機械開關調整變壓器分接頭的速度緩慢，這種機械式PST只適用于電力系統的穩態調整。為了達到抑制系統SSO的目的，本文選用晶閘管控制的移相器，響應速度較快（10～20 ms），可滿足電力系統快速控制的要求。

3.1 PST基本原理

為了更清晰直觀地闡明PST的構造及功能，文中仍以典型的機械式PST為例進行原理分析，其結構如圖4所示。

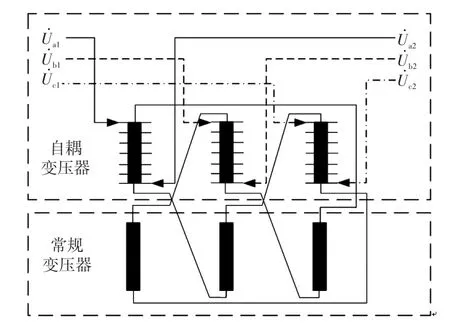
圖4 PST結構Fig.4 Structure of PST

PST由1個自耦變壓器和1個常規變壓器構成，自耦變壓器的原/副邊分別對應PST的原/副邊。自耦變壓器變比可調，常規變壓器副邊對接入的自耦變壓器原邊電壓進行變換，并將該電壓疊加在自耦變壓器副邊，從而實現PST輸出電壓幅值、相位改變。根據PST的聯結結構，PST輸出電壓為

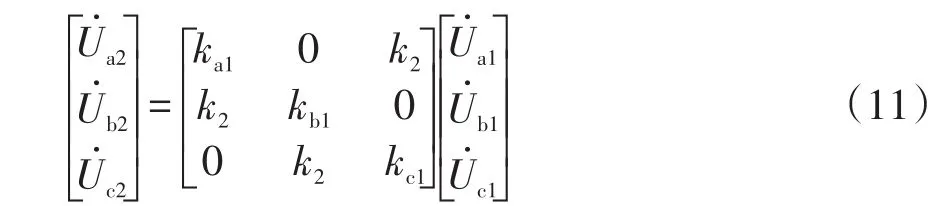
令式（11）中ka1=kb1=kc1=1，則得到如圖5所示的PST電壓調節相量圖。可以看出，PST輸出電壓幅值減小，輸出電壓相位超前輸入電壓α。因此，通過調整自耦變壓器繞組極性與有載分接頭位置以改變其變比，進而實現PST輸出電壓幅值和相位的調節。

圖5 PST相量圖Fig.5 Phasor diagram of PST

3.2 基于PST的SSO抑制方法

針對系統運行工況復雜多變、SSO頻率具有多樣性的問題，本文提出利用PST抑制PSMG接入弱交流電網的SSO。基于前面闡述的SSO發生機理，即GSC與弱交流電網的交互作用，通過在PCC處附加PST，阻斷GSC與弱交流電網的交互進而抑制SSO。

附加PST后的系統拓撲結構如圖6所示。由于PST本身存在一定電阻，一直串入系統中存在功率損耗。因此，在PST和線路兩端各裝設兩臺斷路器，當系統穩定運行時，線路兩端斷路器處于合閘狀態，PST的兩端斷路器處于斷開狀態；當監測到系統發生SSO時，線路上的斷路器斷開，PST的兩端斷路器合閘。

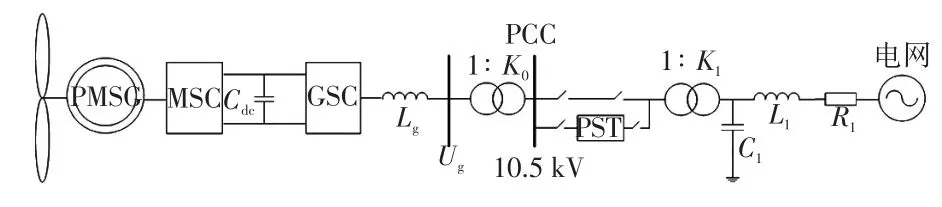
圖6 附加PST的系統拓撲結構Fig.6 System topology with PST

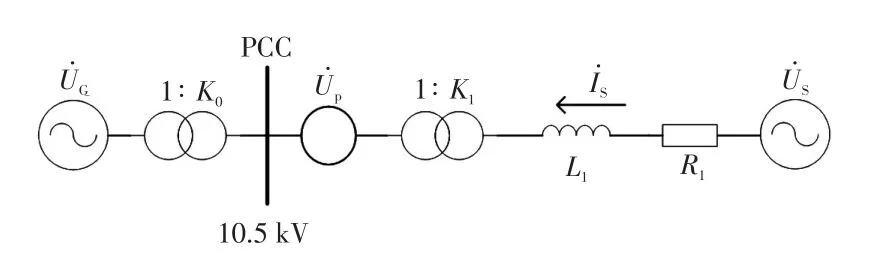
圖7 PST與簡化系統聯結的示意Fig.7 Diagram of PST connected to simplified system

根據圖7可以得出系統的等值阻抗為

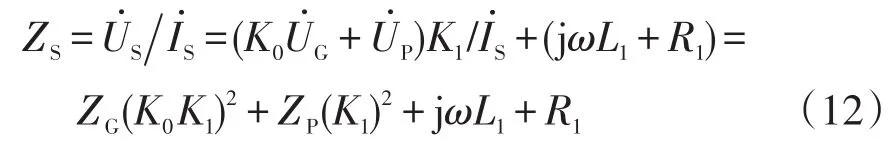
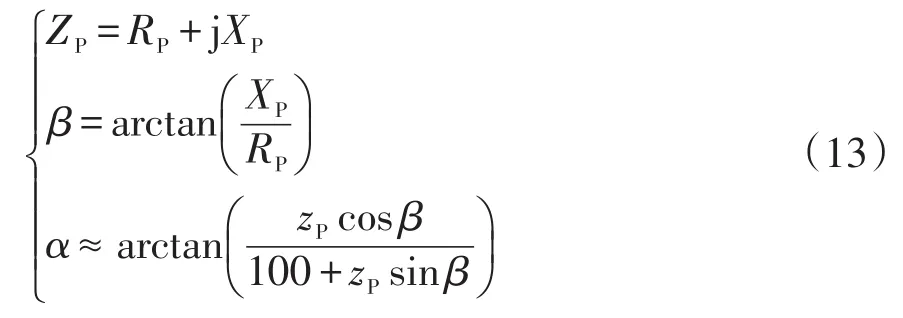
式中：zP為ZP對應的標幺值；RP、XP分別為PST的電阻和電抗；β為負載移相角；α為移相角，調節范圍為 0°～±120°。由式（13）可知，改變PST的移相角α，可以改變ZP的大小。進一步分析可知，當0°＜α＜90°時，隨著α的增大，RP增大、XP減小。

考慮到電壓等級的轉換，則附加PST后的系統阻抗由PMSG等值阻抗ZG、PST等值阻抗ZP和輸電線路等值阻抗(jωL1+R1)三者組成。

文獻[19-20]研究發現PSMG在次同步頻率下具有負電阻(R0)和容性電抗(C0)效應，即PSMG等值阻抗ZG=(R0+1/ jωC0)。基于此，將次同步頻率下的系統等效為如圖8（a）所示的RLC二階諧振電路，其中R∑=R0+R1且有R∑＜0。由式（12）可知，將附加PST的等值電路等效為如圖8（b）所示電路，相比于圖8（a）增加了1個由PST產生的可變RLC。在適當的移相角α下，PST的等值電阻可補償PMSG的負電阻，實現聚合后的等值電阻為正，即R∑+RP＞0。此時，RLC二階等值電路的特征根實部為負，系統表現為正阻尼，達到抑制SSO的目的。

圖8 RLC二階等值電路演變Fig.8 Evolution of RLC second-order equivalent circuit

圖9顯示了PST移相角與SSO工況的關系，即PST及其控制系統實時監測并提取PCC處的SSO頻率分量，并將頻率的偏差作為控制環節的輸入量，PST的移相角為被控量。不同工況下，系統SSO頻率分量不同，控制環節輸入量不同，PST晶閘管的開關順序根據輸入量實時調整，從而使PST的移相角發生相應改變，直到PCC處頻率跟蹤給定值（50 Hz），此時SSO現象得到抑制，系統恢復穩定運行狀態。

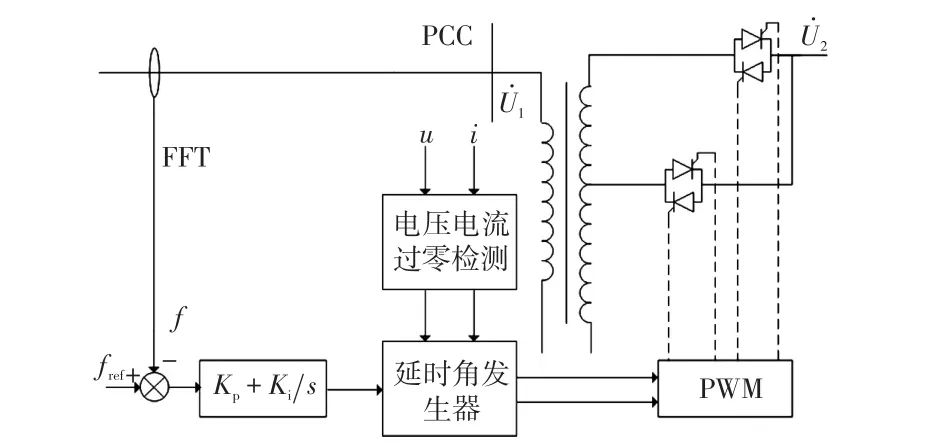
圖9 晶閘管控制的PST的控制框圖Fig.9 Control block diagram of thyristor-controlled PST

4 PST抑制SSO的適應性研究

在Matlab/Simulink建立圖6所示的仿真模型，并按表1設置參數。基于該模型，研究電網強度、風速、風機臺數變化時文中所提抑制方法的適應性。由于電網強度、風速和風機臺數的運行工況改變，PMSG等值負電阻、SSO頻率會相應改變，根據第3.2節分析，PST的移相角會隨頻率偏差相應作出改變，以補償PMSG的負電阻。本文首先通過測量系統等值阻抗驗證PST抑制方法的合理性，其次通過仿真驗證PST對SSO的抑制效果。

4.1 電網強度變化

考慮到電網強度是影響直驅風場SSO的關鍵因素，電網強度越弱，SSO程度越劇烈，因此有必要研究SSO抑制方法對不同電網強度的適應能力。

設置PMSG運行于7 m/s，通過改變輸電線路的電感L1分別設置SCR為2.2和2.0，保持其他電氣參數不變。在t=2 s時，投入PST，研究PST在不同SCR下對SSO的抑制能力。不同SCR下，系統等值阻抗如表3所示，風機出口處A相電壓波形及其頻譜分布如圖10所示。

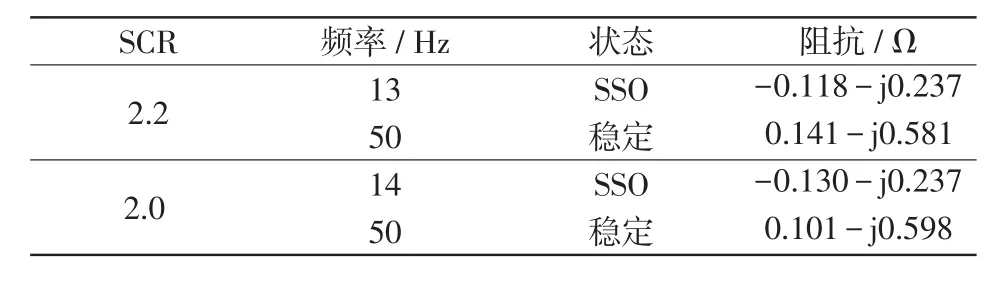
表3 不同SCR下的系統等值阻抗Tab.3 System equivalent impedance under different values of SCR

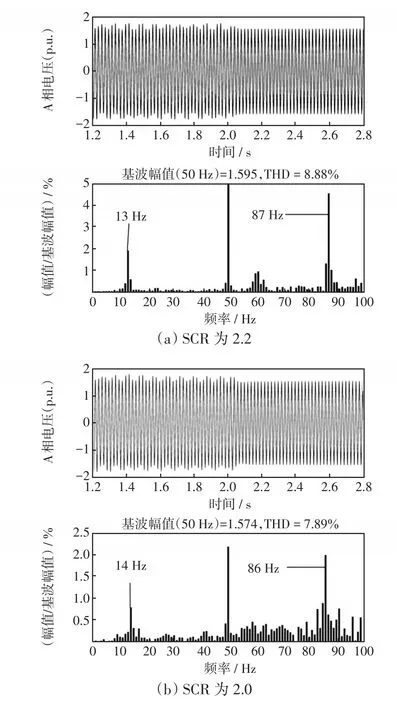
圖10 不同SCR下A相電壓波形及其頻譜分布Fig.10 Waveforms of phase-A voltage and its spectrum distribution under different values of SCR

根據表3，在不同弱電網強度下，系統等效次同步電阻均為負，構成RLC諧振電路，引發PMSG并網系統SSO；投入PST后，系統恢復穩定，系統等效電阻為正，表現為正阻尼，從而抑制SSO。

如圖10（a）所示，設置SCR為2.2，電壓波形呈現SSO，并取t=2 s之前的波形作FFT分析，頻譜圖中顯示SSO頻率為13 Hz；t=2 s后投入PST，電壓波形恢復穩定。同樣地，如圖10（b）所示，設置SCR為2.0，電壓波形呈現SSO，對應的頻譜圖顯示SSO頻率為14 Hz；t=2 s后投入PST，電壓波形恢復穩定。綜上，一方面，根據頻譜圖可以得出電網強度變化對SSO的具體影響趨勢，即隨著電網強度的降低，SSO頻率增大；另一方面，通過在PCC處附加PST可以在不同電網強度下，無區別地抑制不同頻率的SSO。

4.2 風速變化

由于風速是影響直驅風場SSO的重要因素，并且實際風場中風速具有隨機性、波動性等特點，因此有必要研究SSO抑制方法對不同風速的適應能力。

設置PMSG分別運行于10 m/s、6 m/s，SCR恒為2.0，保持其他電氣參數不變。在t=2 s時，投入PST，研究PST在不同風速下對SSO的抑制能力。不同風速下，系統等值阻抗如表4所示，風機出口處A相電壓波形及其頻譜分布如圖11所示。

表4 不同風速下的系統等值阻抗Tab.4 System equivalent impedance under different wind speeds

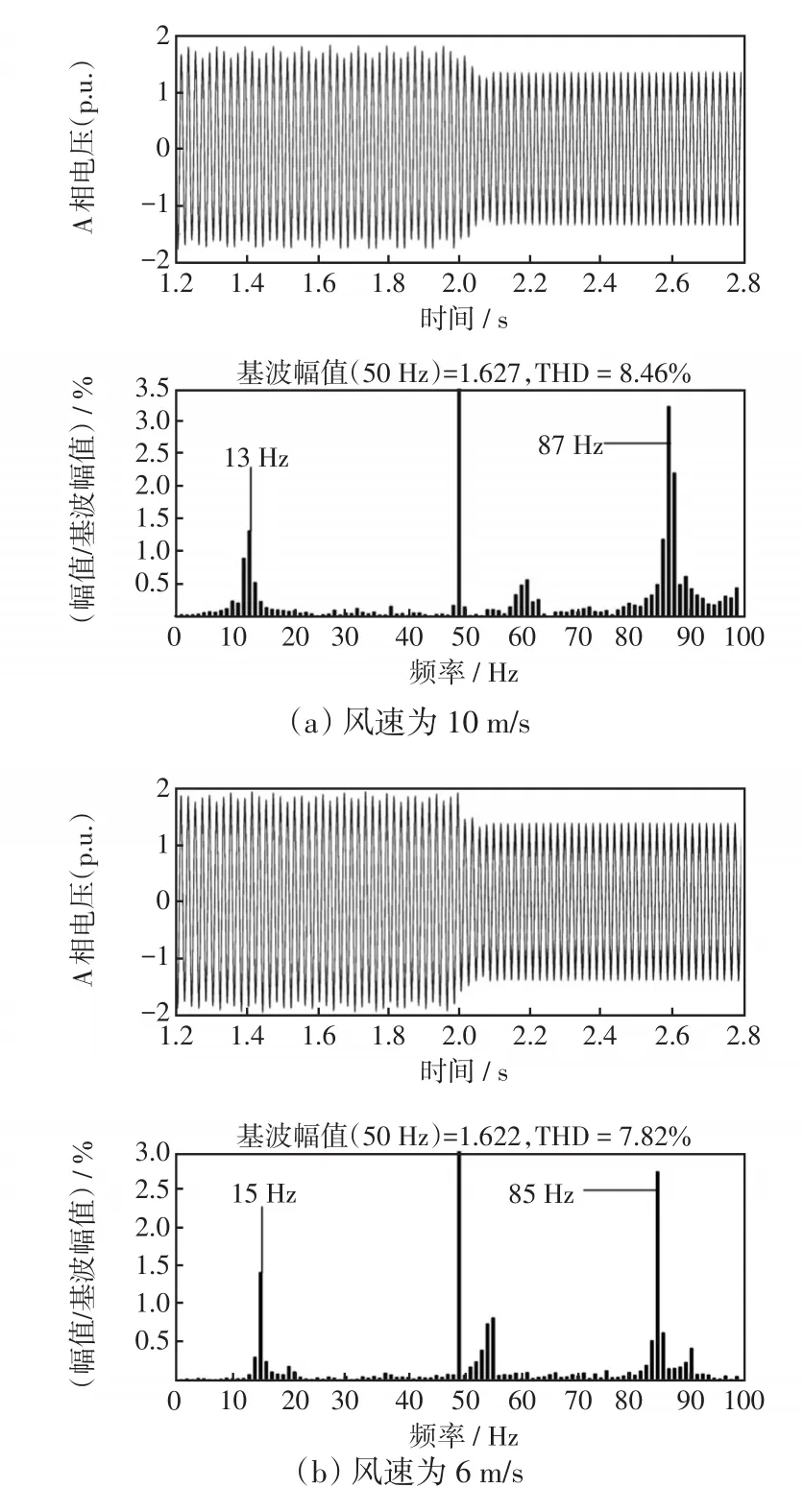
圖11 不同風速下A相電壓波形及其頻譜分布Fig.11 Waveforms of phase-A voltage and its spectrum distribution under different wind speeds

根據表4，在不同風速下，系統等效次同步電阻均為負，構成RLC諧振電路，引發PMSG并網系統SSO；投入PST后，系統恢復穩定，系統等效電阻為正，表現為正阻尼，從而抑制SSO。

如圖11（a）所示，設置風速為10 m/s，電壓波形呈現SSO，并取t=2 s之前的波形作FFT分析，頻譜圖中顯示SSO頻率為13 Hz；t=2 s后投入PST，電壓波形恢復穩定。同樣地，如圖11（b）所示，設置風速為6 m/s，電壓波形呈現SSO，對應的頻譜圖顯示SSO頻率為15 Hz；t=2 s后投入PST，電壓波形恢復穩定。綜上，一方面，根據頻譜圖可以得出風速變化對SSO的具體影響趨勢，即隨著風速的減小，SSO頻率增大；另一方面，通過在PCC處附加PST可以在不同風速下，無區別地抑制不同頻率的SSO。

4.3 風機臺數變化

前述SSO研究均以單機模型為研究對象，但考慮到風機臺數是影響直驅風場SSO的重要因素，并且風場中實際投入運行的風機臺數會根據用電負荷需求變化而調整，因此有必要研究SSO抑制方法對不同風機臺數的適應能力。

設置分別投入2臺、3臺風機，SCR恒為2.0，風速恒為11 m/s，保持其他電氣參數不變。在t=2 s時，投入PST，研究PST在不同風機臺數下對SSO的抑制能力。不同風機臺數下，系統等值阻抗如表5所示，風機出口處A相電壓波形及其頻譜分布如圖12所示。

表5 不同風機臺數下的系統等值阻抗Tab.5 System equivalent impedance under different numbers of fans

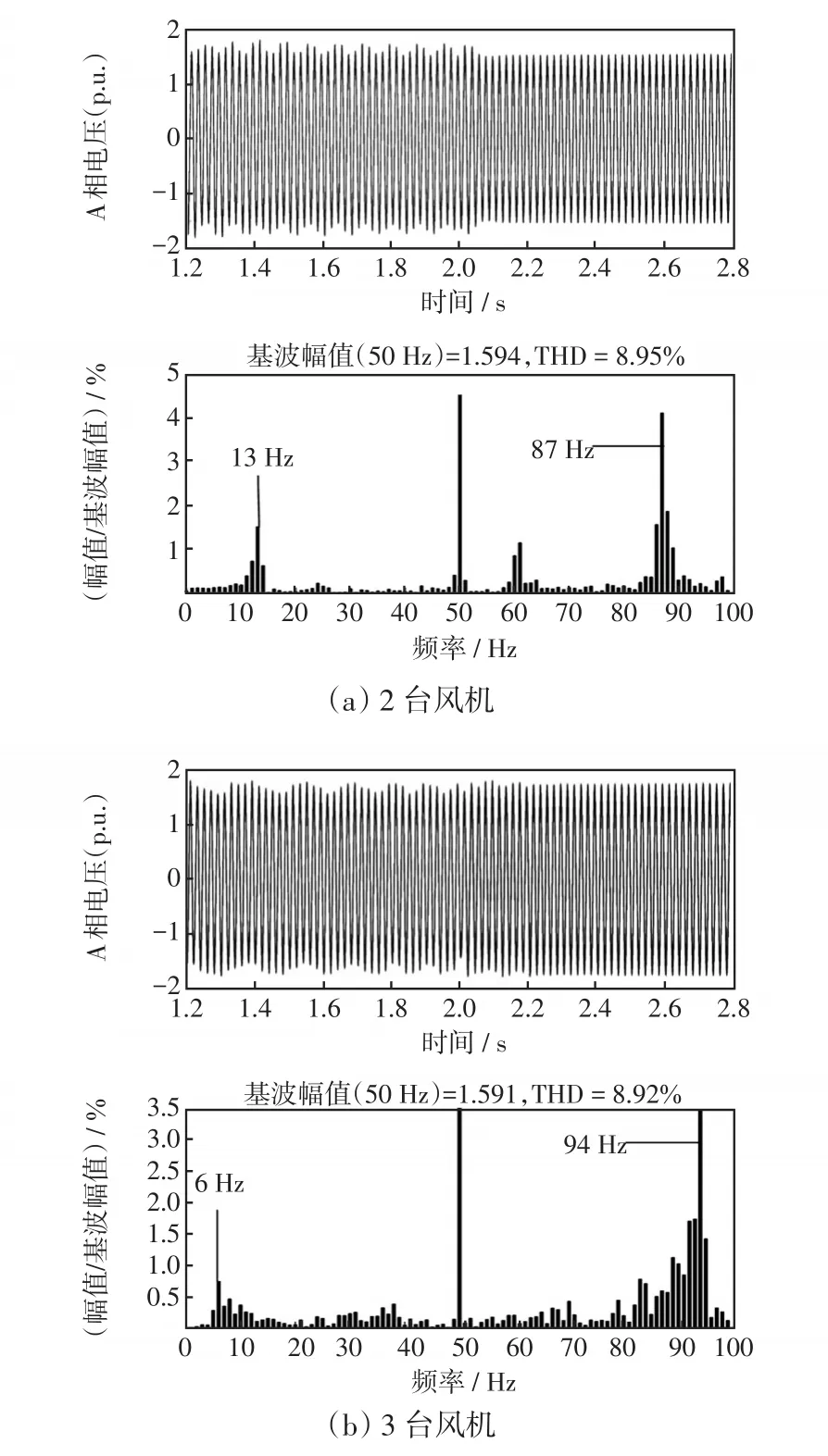
圖12 不同風機臺數下A相電壓波形及其頻譜分布Fig.12 Waveforms of phase-A voltage and its spectrum distribution under different numbers of fans

根據表5，在不同風機臺數下，系統等效次同步電阻均為負，構成RLC諧振電路，引發PMSG并網系統SSO；投入PST后，系統恢復穩定，系統等效電阻為正，表現為正阻尼，從而抑制SSO。

如圖12（a）所示，投入2臺風機，電壓波形呈現SSO，并取t=2 s之前的波形作FFT分析，頻譜圖中顯示SSO頻率為13 Hz；t=2 s后投入PST，電壓波形恢復穩定。同樣地，如圖12（b）所示，投入3臺風機，可以看到電壓波形呈現SSO，對應的頻譜圖顯示SSO頻率為6 Hz；t=2 s后投入PST，電壓波形恢復穩定。綜上，一方面，根據頻譜圖可以得出風機臺數變化對SSO的具體影響趨勢，即隨著風機臺數的增加，SSO頻率減小；另一方面，通過在PCC處附加PST可以在不同風機臺數下，無區別地抑制不同頻率的SSO。

上述仿真研究驗證了基于PST的PMSG的SSO抑制方法的合理性及其較好的適應性，但是該方法也存在以下3點不足：①串入PST會存在功率損耗，PST的移相角越大，其等值電阻越大，功率損耗越大；②串入PST會產生諧波污染，由于晶閘管工作在斬波狀態，PST輸出的電壓中含有較大的諧波分量，而含諧波電壓會在負荷中產生諧波電流，進而可能造成電動機發熱等；③投入PST會對線路產生沖擊，造成線路電壓降落等。

5 結論

（1）建立了PMSG接入弱交流電網的小信號模型，通過特征值與參與因子分析確定了PMSG接入弱交流電網的SSO由GSC與弱交流電網交互作用引發。

（2）針對實際風機并網系統運行工況多變、SSO頻率具有多樣性的問題，提出了一種基于PST的SSO抑制方法。

（3）從系統等值阻抗角度分析了PST抑制SSO的原理，在適當移相角下PST等值電阻可補償PMSG負電阻，從而增強系統阻尼，達到抑制SSO的目的。

（4）在不同電網強度、風速和風機臺數下，系統等效次同步電阻為負，引發系統SSO；投入PST后，系統等效電阻為正，系統恢復穩定。

（5）各個工況下的波形及其頻譜圖表明PST能夠無區別地抑制不同頻率的SSO，驗證了PST對SSO抑制的適應性。

然而，目前國內對PST的工程應用還不成熟，本文初步嘗試利用PST解決直驅風場SSO問題。引入PST還存在功率耗散、諧波污染和線路沖擊等問題，同時對于PST的選址和容量規劃等還需進一步研究。另外，PST作為一種靈活的潮流調控裝置，能夠在不改變機組輸出功率、系統拓撲結構的情況下有效地調節電網潮流，具有廣闊的應用前景。