基于多種失效模式及其隨機(jī)相關(guān)性的地下管道腐蝕可靠性分析

王曉敏，駱正山，高懿瓊，孔玉磊

基于多種失效模式及其隨機(jī)相關(guān)性的地下管道腐蝕可靠性分析

王曉敏，駱正山，高懿瓊，孔玉磊

（西安建筑科技大學(xué) 管理學(xué)院，西安 710055）

考慮不同時間點(diǎn)載荷效應(yīng)過程的相關(guān)性以及不同失效模式之間的相關(guān)性，提出了一種確定受腐蝕影響的具有多種失效模式的地下鋼管系統(tǒng)失效概率的方法。失效鋼管受腐蝕的形態(tài)包括斷裂、強(qiáng)度破壞、撓度和屈曲，它們都是隨機(jī)過程，并相互關(guān)聯(lián)。采用高斯過程的第一通道概率理論對其進(jìn)行量化，蒙特卡羅模擬在每個時間點(diǎn)計(jì)算均值函數(shù)μ()和標(biāo)準(zhǔn)差σ()負(fù)載效應(yīng)的過程，相關(guān)矩陣包含不同失效模式之間的相關(guān)系數(shù)作為時間的函數(shù)，計(jì)算了各失效模式的失效概率，然后通過考慮不同失效模式之間的相關(guān)性確定了系統(tǒng)的失效概率。通過一個案例研究來驗(yàn)證該方法的可靠性，并通過敏感性分析，研究關(guān)鍵變量對腐蝕鋼管失效概率的影響。不同失效模式之間的相關(guān)性以及失效事件在時間維度上的相關(guān)性，對單一模式的失效概率以及系統(tǒng)失效概率的量化評價具有較大的影響，在諸多影響因子中，腐蝕模型中的乘數(shù)常數(shù)、指數(shù)常數(shù)和管厚對失效概率的影響最大。隨管道使用年限的增加，與有增大的趨勢，值的上限在不同的失效模式下均可達(dá)到0.8以上，則可增至–0.2以上；同時，逐年減小，其最低值可降至0.2左右。考慮時變因素的可靠性算法是腐蝕影響下的埋地鋼管失效評估的有效工具，對腐蝕作用下的埋地鋼管進(jìn)行失效預(yù)測，確定時間維度上管道相關(guān)位置載荷作用過程的自相關(guān)系數(shù)和不同失效模式之間的相關(guān)性，能夠提高管道失效概率預(yù)測的準(zhǔn)確性。

腐蝕；失效模式；可靠性；相關(guān)性分析

地下管道主要由鋼材構(gòu)成，為工業(yè)生產(chǎn)和居民生活輸送生產(chǎn)生活必需品。腐蝕是造成埋地鋼質(zhì)管道破壞的主要原因之一，腐蝕發(fā)生的影響因素眾多，包括埋地管道外界因素、土壤腐蝕性、管道防腐層質(zhì)量和管道本身的損傷程度等[1-2]。地下管道由于長期暴露在腐蝕性環(huán)境中，鋼管的防護(hù)措施（涂漆、陰極保護(hù)或鍍鋅等）可能失效，不可避免地導(dǎo)致鋼管變質(zhì)和損壞。隨著石油天然氣工業(yè)的發(fā)展，管道布網(wǎng)增密，管道鋪設(shè)環(huán)境復(fù)雜，運(yùn)行時間增長，由管道腐蝕引發(fā)的生產(chǎn)事故時有發(fā)生，對社會經(jīng)濟(jì)以及生態(tài)環(huán)境產(chǎn)生了嚴(yán)重的影響，因此管道腐蝕對管道可靠性的影響成為研究熱點(diǎn)[3]。1969年，F(xiàn)olias就提出了半經(jīng)驗(yàn)斷裂力學(xué)關(guān)系式。在這一理論背景下，德克薩斯州東部輸氣公司和美國天然氣協(xié)會（AGA）的管道研究委員會，共同針對腐蝕影響下的管道剩余強(qiáng)度評價問題展開了研究，并提出了一項(xiàng)被稱為B31G的準(zhǔn)則，用于評價腐蝕管道的可用性。20世紀(jì)90年代中期，管道失效檢測與評價問題逐漸受到國內(nèi)管道專家的重視，相關(guān)研究成果得到了相關(guān)企業(yè)的高度重視和積極應(yīng)用，使得管道失效診斷和模型評價技術(shù)也得到了長足的發(fā)展。

研究表明，鋼管失效主要是由材料變質(zhì)（主要是腐蝕）和外加載荷共同作用造成的。大多數(shù)與管道失效相關(guān)的參數(shù)，如管道幾何形狀、材料特性、外部載荷和腐蝕過程，都表現(xiàn)出不同程度的變化，也可能隨時間而變化。考慮到這些參數(shù)的不確定性和時變性，在評估管道失效時須采用隨機(jī)方法。已有研究表明，一根鋼管可能會在不同的模式下失效，其中包括強(qiáng)度破壞、泄漏或塑性崩潰等。針對不同失效模式下的鋼管設(shè)計(jì)和失效評估，已經(jīng)建立了不同的準(zhǔn)則。Ahammed等[4]不僅考慮了箍應(yīng)力引起的腐蝕管道的強(qiáng)度破壞，并使用一階可靠度方法來量化不確定性。De Silva等[5]提出了一種基于概率分析的條件評估來估計(jì)故障率。在分析中，僅考慮環(huán)向應(yīng)力，并結(jié)合條件評估數(shù)據(jù)采用一階、二階矩法確定失效概率。Melchers[6]應(yīng)用定常理論對受點(diǎn)蝕的管道進(jìn)行可靠性分析，認(rèn)為當(dāng)最大點(diǎn)蝕深度達(dá)到管道厚度時，就會發(fā)生失效。Awwa[7]采用蒙特卡羅模擬方法研究了韌性金屬管道的失效概率，其極限狀態(tài)函數(shù)由失效壓力與工作壓力之差定義。綜上所述，以往的研究大多僅采用一階可靠度法或蒙特卡羅模擬法來確定失效概率。有關(guān)管道的時變可靠度研究較少，這表明了相關(guān)性在時域退化過程中沒有被考慮。

地下管道往往有多段，每一段可能包含多個腐蝕缺陷，其失效形式可能不同，有學(xué)者綜合考慮了多種失效模式對管道可靠性的影響。Li等[8]提出了一種綜合評估管道段可靠性的方法，考慮了小泄漏、大泄漏和破裂等3種破壞模式，并通過蒙特卡洛方法對內(nèi)部壓力的隨機(jī)變化過程進(jìn)行模擬，并進(jìn)一步計(jì)算失效概率。Yu等[9]考慮了腐蝕引起的撓度、屈曲、壁推力和彎曲應(yīng)力等失效模式，采用子集模擬方法進(jìn)行地下柔性管道時變可靠性預(yù)測。Fu等[10]對一段腐蝕埋地管道進(jìn)行了基于分段的系統(tǒng)可靠性分析，該管道各分段存在多處腐蝕缺陷，并采用蒙特卡羅模擬技術(shù)對爆管進(jìn)行可靠性分析，采用分裂系統(tǒng)方法對可靠性預(yù)測進(jìn)行更新。然而，以上研究均認(rèn)為失效模式是獨(dú)立的，對不同失效模式下的概率進(jìn)行累加導(dǎo)致系統(tǒng)失效概率被高估。

本文考慮不同時間點(diǎn)載荷效應(yīng)過程的相關(guān)性以及不同失效模式之間的相關(guān)性，提出了一種確定受腐蝕影響的具有多種失效模式（包括管道破裂）的地下鋼管系統(tǒng)失效概率的方法。失效鋼管受腐蝕的形態(tài)包括斷裂、強(qiáng)度破壞、撓度和屈曲。所有失效模式下的載荷效應(yīng)都被建模為高斯過程。利用高斯過程的第一通道概率理論計(jì)算了各失效模式的失效概率，然后通過考慮不同失效模式之間的相關(guān)性確定系統(tǒng)的失效概率，并通過一個案例來說明所提出的方法。將腐蝕鋼管的各種失效模式假設(shè)為一個系統(tǒng)，計(jì)算腐蝕鋼管的系統(tǒng)失效概率，然后進(jìn)行敏感性分析，研究關(guān)鍵變量對腐蝕鋼管失效概率的影響。

1 系統(tǒng)可靠性公式

在評估地下管道失效的風(fēng)險(xiǎn)時，應(yīng)建立性能標(biāo)準(zhǔn)。在結(jié)構(gòu)可靠度理論[11]中，各失效準(zhǔn)則以極限狀態(tài)函數(shù)（Limit State Function，LSF）的形式表示為：

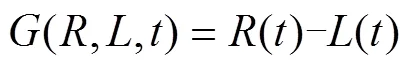
式中：()為時刻的荷載；()為阻力。由式（1）的極限狀態(tài)函數(shù)，可以確定地下管道失效概率如式（2）所示，其中表示一個事件的概率。

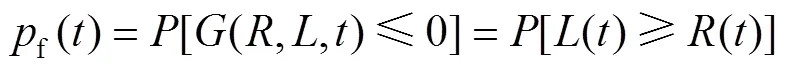
一個管段可能包含種失效模式，可以看作是一個系統(tǒng)[12]。根據(jù)基本集合理論，管段的失效概率可以表示為：

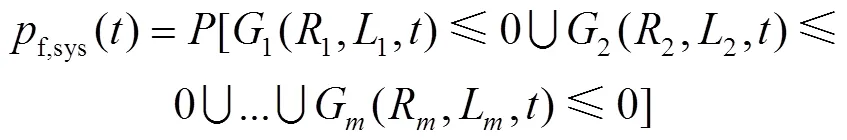
式中：G為種失效模式的極限狀態(tài)；r為種失效模式的電阻；l為種失效模式的載荷效應(yīng)。

實(shí)際中，地下管道的失效模式之間有一定聯(lián)系。考慮到其相關(guān)性，管道系統(tǒng)的失效概率[13]可以用式（4）近似方法計(jì)算。其中，=(1，2，β)是一個向量的分量，為種失效模式的可靠性指標(biāo)。

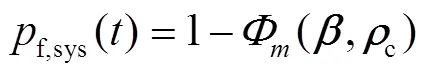
每一種失效模式的失效概率可以用式（2）計(jì)算，這是一個典型的上行交叉問題，可以用時變可靠性方法處理。時變可靠性問題是指將所有或部分基本隨機(jī)變量建模為隨機(jī)過程的問題。在依賴時間的可靠度方法中，地下管道失效取決于在管道使用壽命中某一時刻，作用過程()向上跨越可接受的極限()之前預(yù)期的時間。同樣地，這種偏移第一次發(fā)生的概率等于該時間段內(nèi)管道失效的概率。這就是所謂的第一通道概率[14]，在泊松過程的假設(shè)下，它可以表示為：

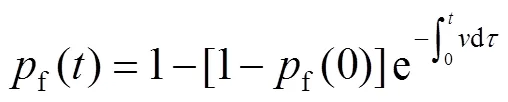
式中：f(0)為=0時刻管道失效的概率；f()為響應(yīng)過程()向上越過閾值()的平均率。值得注意的是，對于可靠性問題，向上交叉通常很少發(fā)生，因此通常將單個向上交叉假設(shè)為獨(dú)立事件，從而獨(dú)立于任何早期的向上交叉的概率，包括=0時的向上交叉。式(5)中的上交率可由公式（6）確定。

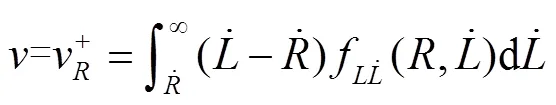
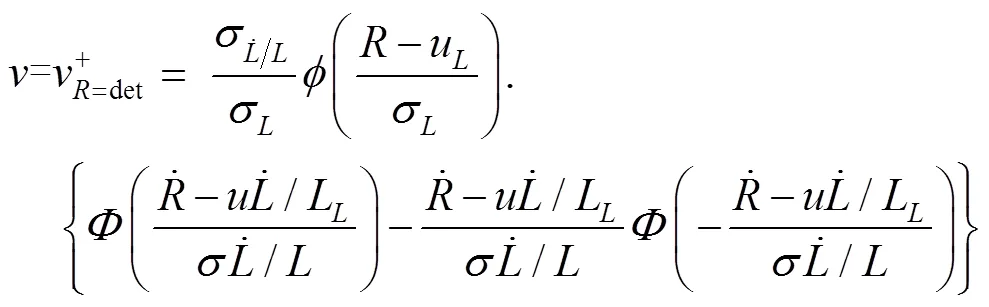
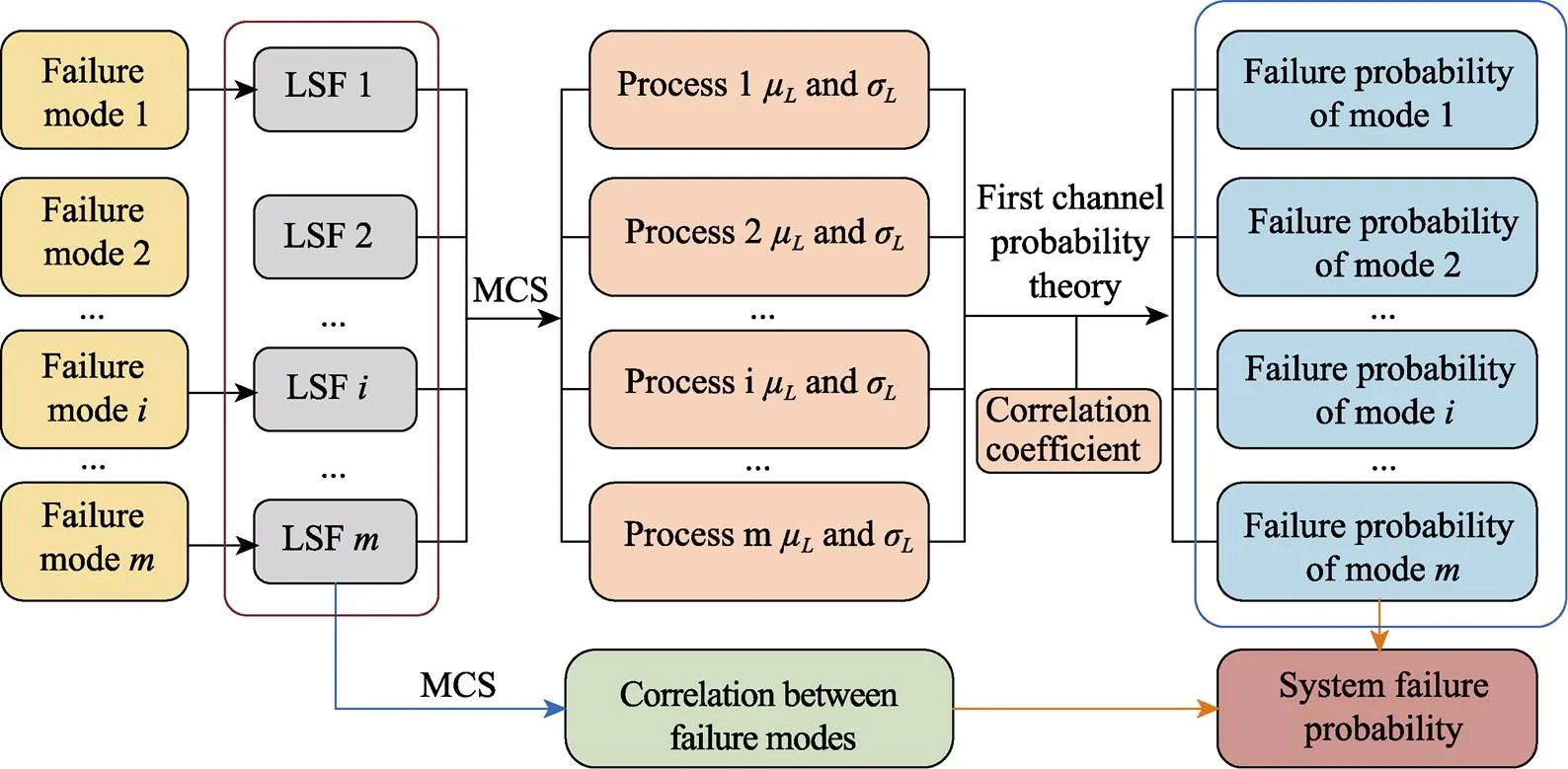
圖1 計(jì)算系統(tǒng)故障概率的流程

2 鋼管的失效模式

2.1 斷裂

對于韌性材料，Lin等[16]建立了傾斜裂紋誘導(dǎo)的混合模式斷裂管道的彈性斷裂韌性模型。利用所建立的模型評估韌性金屬管道斷裂條件的失效準(zhǔn)則見式（8）。其中e為考慮所有斷裂模式的等效應(yīng)力強(qiáng)度因子，見式（9）。

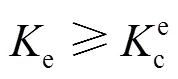
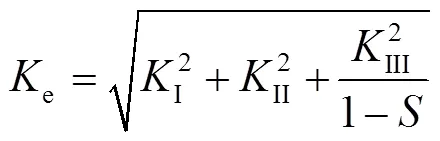
式中：I、II、III是模式I、II、III的壓力強(qiáng)度因子；為泊松比[17]。；ce為彈性斷裂韌性，見式（10）。

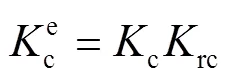
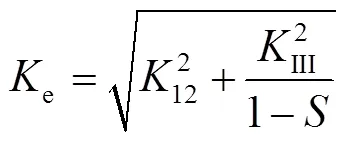
rc由式（12）計(jì)算[18]，其中是橢圓的形狀因子，由第二類完全橢圓積分的平方給出。

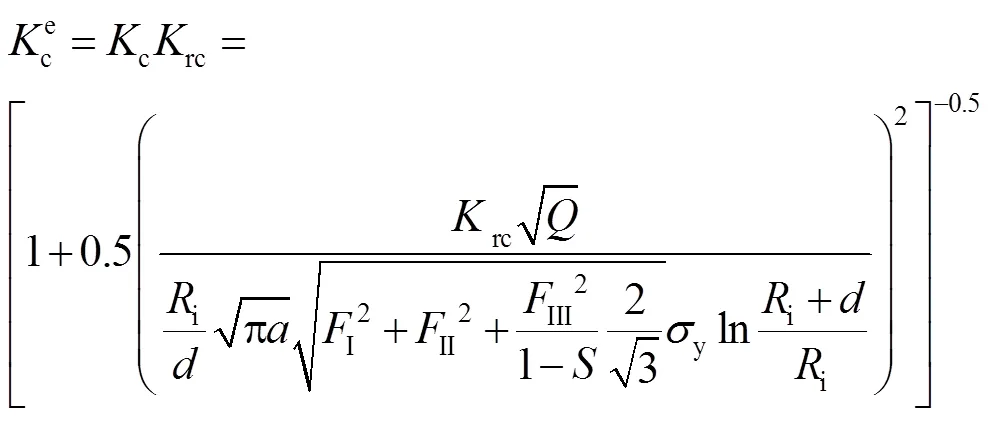
2.2 強(qiáng)度失效

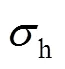
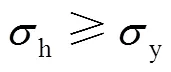
對于薄壁管材，可以通過考慮外部土體和交通荷載產(chǎn)生的內(nèi)壓和彎曲應(yīng)力來計(jì)算環(huán)向應(yīng)力，其表達(dá)式為[20]：

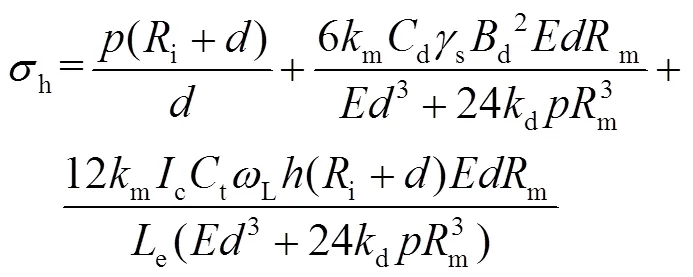
式中：是內(nèi)部壓力；m是一個彎矩系數(shù)；d是地球負(fù)荷；s是土壤單位質(zhì)量；d為管道頂部的溝渠寬度；m是管道的平均半徑；d是偏轉(zhuǎn)系數(shù)；c是影響因子；t是表面負(fù)載系數(shù)；l是車輪負(fù)載；是回填的高度；e是計(jì)算荷載的管道的有效長度。

2.3 偏轉(zhuǎn)失效

在外載荷作用下，柔性鋼管有變形的傾向。在本研究中，撓度破壞采用的破壞準(zhǔn)則[21]見式（15）。其中，是地下管道的水平撓度，可由公式（16）計(jì)算。

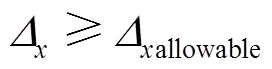
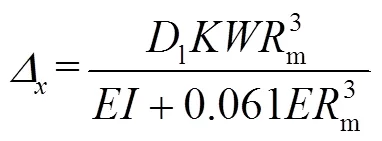
式中：l為撓度滯后系數(shù)；為層理常數(shù)；為單位長度管道外荷載；為管道壁剛度；為單位長度管道橫向慣性矩；為土壤反體模量。允許的管道撓度為各種襯里和涂層系統(tǒng)范圍的2%～5%。在本文中，管道的允許撓度為管徑的3%。當(dāng)水平撓度超過管道允許撓度時，就認(rèn)為管道失效。

2.4 屈曲失效

埋在地下的管道由于外荷載和變形引起彈性失穩(wěn)而發(fā)生倒塌或屈曲。因此，外載荷的總和不應(yīng)大于許用屈曲壓力。鋼管上的外荷載[20]可以表示為：

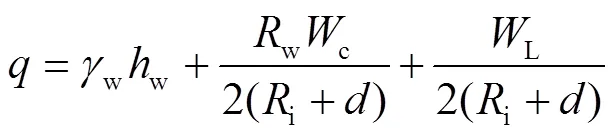
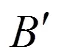
表1 隨機(jī)變量的統(tǒng)計(jì)特性

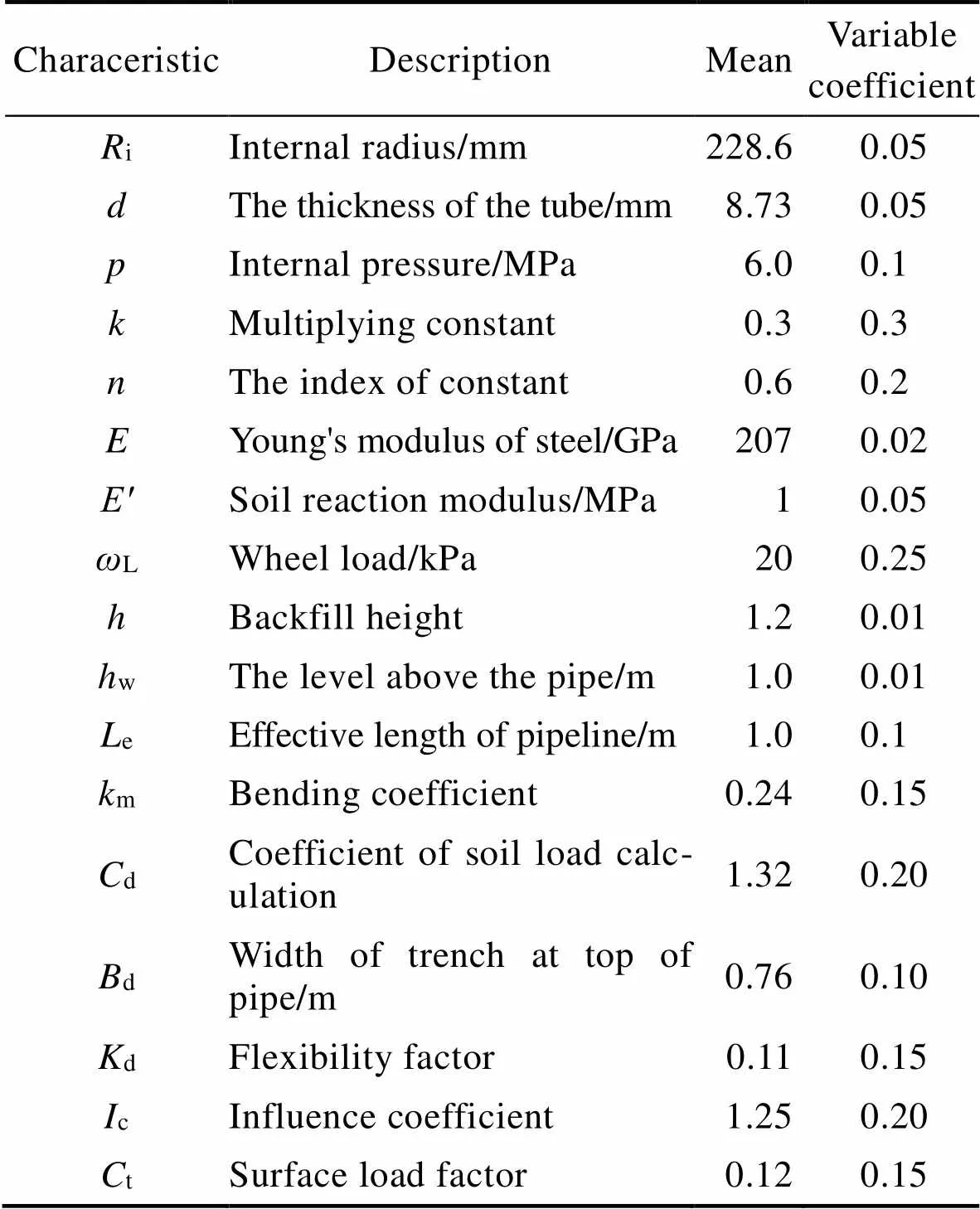
Tab.1 Statistic properties of random variables

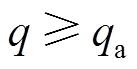
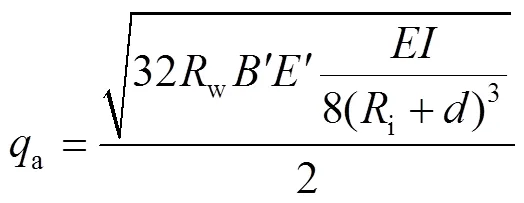
3 載荷效應(yīng)的隨機(jī)模型

眾所周知，腐蝕過程是一個非常隨機(jī)的現(xiàn)象，取決于局部條件，如土壤類型、濕度和氧氣含量、埋地管道材料的性質(zhì)等。從現(xiàn)場調(diào)查觀察到，腐蝕可能以均勻腐蝕或點(diǎn)蝕的形式發(fā)生。腐蝕速率是實(shí)時變化的，由于腐蝕產(chǎn)物在表面形成的保護(hù)性能較差，腐蝕速率的初始值較高。

本文采用冪律腐蝕模型來計(jì)算腐蝕坑深，見式（20）。其中和分別是乘法常數(shù)和指數(shù)常數(shù)，這取決于管材和周圍環(huán)境。一般應(yīng)通過試驗(yàn)來確定這2個常數(shù)。但是，在許多情況下，可以根據(jù)已發(fā)表的文獻(xiàn)和過去的經(jīng)驗(yàn)來估計(jì)這2個常數(shù)的值。采用的腐蝕模型，和的均值分別為0.3和0.6，變化系數(shù)分別為0.3和0.2。

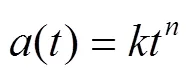
用于評估鋼管失效條件的大多數(shù)參數(shù)不僅不確定，而且還隨時間變化。因此，將它們建模為隨機(jī)過程是合適的。由此可知，表1中定義的荷載效應(yīng)()是基本變量x(=1, 2, …,)和時間的函數(shù)，可以表示為：

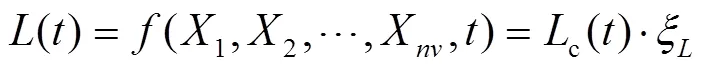
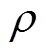
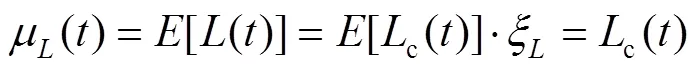
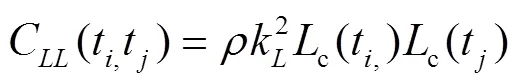
4 應(yīng)用實(shí)例

選取某巷道下埋置的鋼管，對其進(jìn)行時變可靠度分析。假設(shè)保護(hù)層已經(jīng)失效。本例考慮了傾角為0°的斷裂模式，即裂縫1；傾角為30°時的斷裂模式，即裂縫2；同時考慮了強(qiáng)度、撓度和屈曲破壞。假設(shè)斷口尖銳腐蝕坑的長徑比為0.4，只考慮沿裂紋前沿的最深點(diǎn)，作為其應(yīng)力強(qiáng)度的最大因子。鋼的I型斷裂韌性取值為50 MPa，在沿裂紋前沿的最深處，僅存在I型和III型混合斷裂韌性。利用非線性回歸擬合試驗(yàn)結(jié)果，得到公式（24）。其中，e的取值范圍為0～1。

另外，取撓度滯后因子l為1.0，層理常數(shù)為0.1，水的w=9.81 kN/m3，水浮力因子w由式（25）確定[21]。

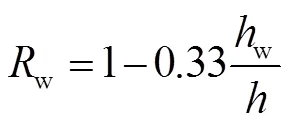
式（16）中的可以表示為：

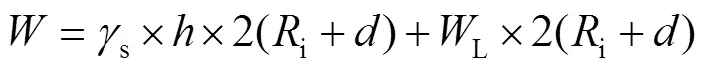
4.1 失效的概率

按照圖1所示的步驟來確定系統(tǒng)故障的概率。蒙特卡洛模擬是通過隨機(jī)變量的統(tǒng)計(jì)試驗(yàn)或隨機(jī)模擬進(jìn)行數(shù)值求解的一種近似方法，由于其求解簡單而廣泛應(yīng)用。蒙特卡洛模擬法計(jì)算管道失效概率和可靠度的具體方法和步驟如圖2所示。

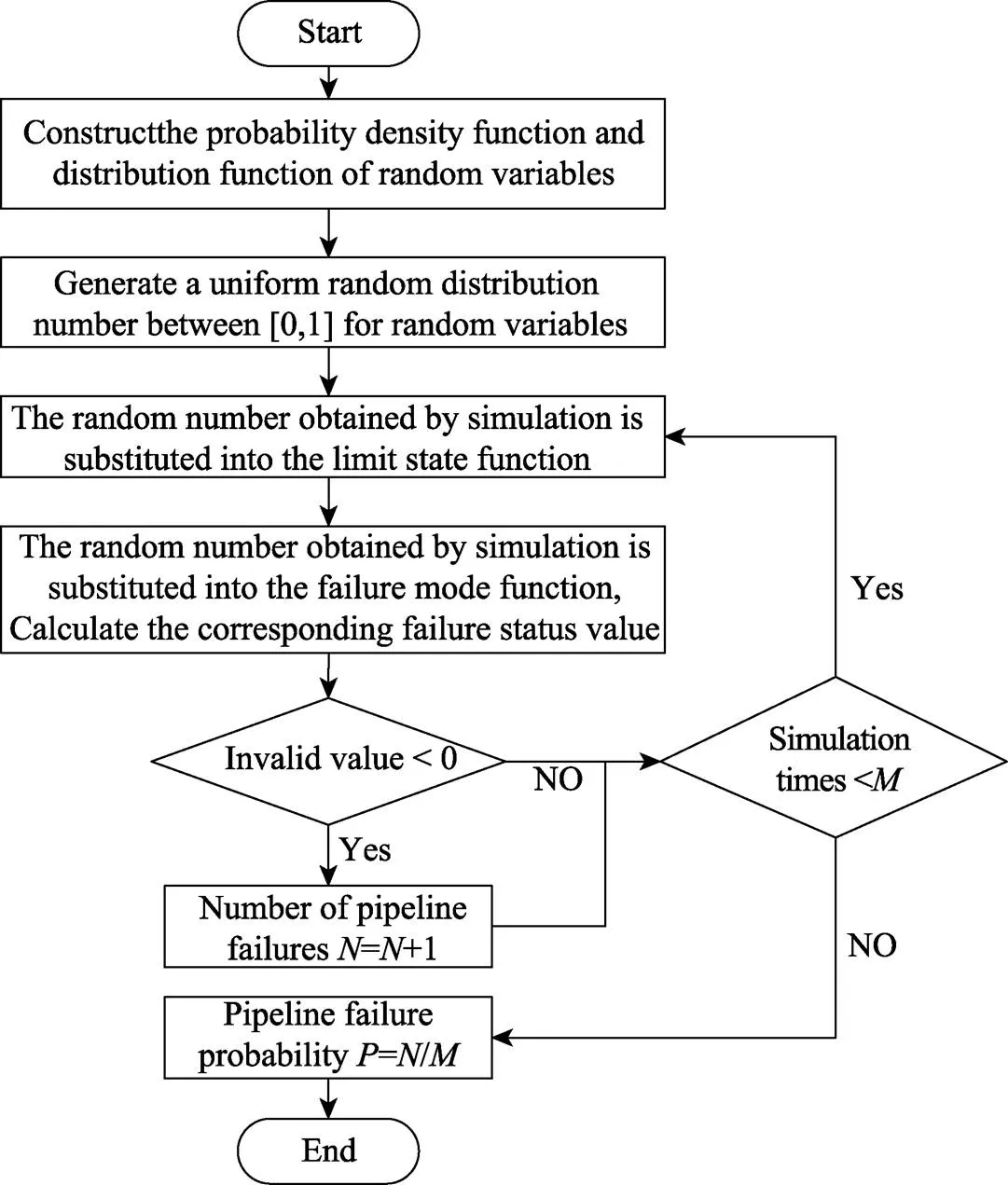
圖2 蒙特卡洛仿真算法流程

1）收集相關(guān)數(shù)據(jù)，進(jìn)行統(tǒng)計(jì)分析，確定隨機(jī)變量的概率密度函數(shù)()和分布函數(shù)()。

2）針對每一個隨機(jī)變量，在[0,1]之間生成許多均勻的隨機(jī)分布數(shù)(x)。

3）將每次模擬得到的隨機(jī)數(shù)代入極限狀態(tài)函數(shù)，對于每個隨機(jī)變量的分布函數(shù)(x)解出相應(yīng)的x，因此對于每個變量x模擬一次可得到一組隨機(jī)數(shù)(1j,2j, …,x)。

4）將每次模擬得到的隨機(jī)數(shù)代入失效模式函數(shù)中，計(jì)算相應(yīng)的失效狀態(tài)值。

5）若失效狀態(tài)值小于0，則管道失效1次，否則管道未失效。

6）重復(fù)步驟第3、第4、第5步，共計(jì)進(jìn)行次模擬，共計(jì)失效次，根據(jù)大數(shù)理論，則失效概率為f=/。

蒙特卡羅模擬在每個時間點(diǎn)計(jì)算均值函數(shù)μ()和標(biāo)準(zhǔn)差σ()負(fù)載效應(yīng)的過程，和相關(guān)矩陣包含不同失效模式之間的相關(guān)系數(shù)作為時間的函數(shù)。蒙特卡羅模擬的樣本容量為5 000。然后，對于每種破壞模式，通過公式(5)計(jì)算管道的破壞概率，給定自相關(guān)系數(shù)，通過公式(7)計(jì)算出上交率。

兩點(diǎn)(t,t)在傾角為=30°時斷裂載荷效應(yīng)過程的自相關(guān)系數(shù)擬合效果如圖3所示。對于其他的失效模式，也可以得到類似的結(jié)果。由此可見，腐蝕對管道失效有相當(dāng)大的影響。因?yàn)楦g對管道失效的影響取決于管道幾何形狀、腐蝕速率、水壓等，這些在不同時間點(diǎn)是相互關(guān)聯(lián)的。因此，載荷效應(yīng)在時域上是相關(guān)的。基于首次通過概率的概念和隨機(jī)過程理論，由于故障概率的巨大差異，有必要采用時變可靠度方法。在實(shí)際應(yīng)用中，需要收集足夠的荷載效應(yīng)過程的時間歷史數(shù)據(jù)，利用統(tǒng)計(jì)方法估計(jì)2個點(diǎn)(t,t)在時間上的荷載效應(yīng)過程的自相關(guān)系數(shù)。

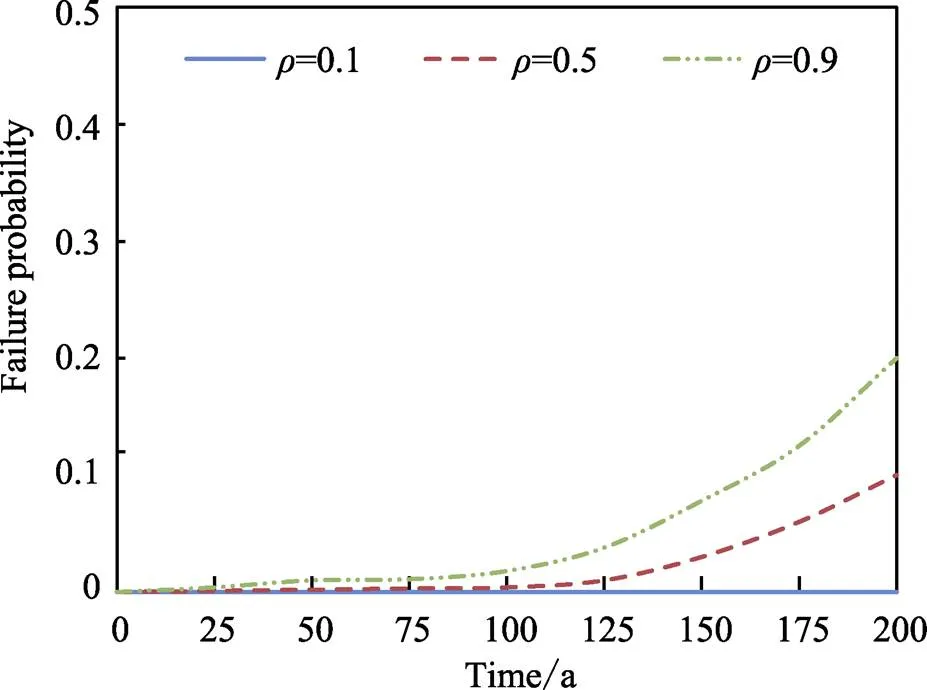
圖3 當(dāng)θ=30°時不同ρ值鋼管的失效概率

將鋼管的所有失效模式視為一個系統(tǒng)，如圖4所示。對于具有上述5種失效模式的系統(tǒng)，系統(tǒng)的可靠性見式（27），其中f1、f2分別代表傾角為0°和30°時的模式，s、d、b分別代表強(qiáng)度、撓度和屈曲的極限狀態(tài)。

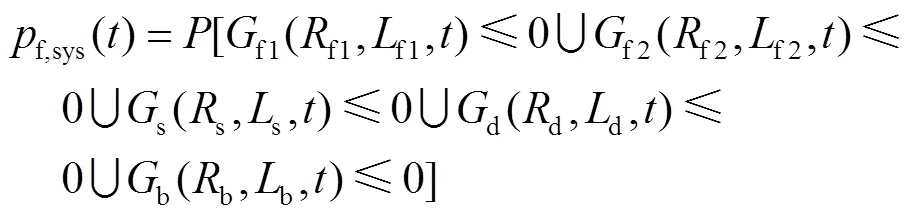
如果不考慮這些失效模式之間的相關(guān)性，則系統(tǒng)失效概率的上界由公式（28）計(jì)算。其中f,f1、f,f2分別代表傾角為0°和30°時的模式，f,s、f,d、f,b分別為斷裂的強(qiáng)度、撓度和屈曲的失效概率。

為了考慮這些失效模式之間的相關(guān)性，系統(tǒng)失效的概率可以寫成：

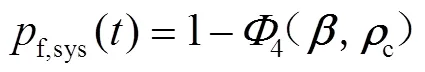
式中：c為包含4種失效模式間相關(guān)系數(shù)的相關(guān)矩陣。通過蒙特卡羅模擬，對4種失效模式的式（1）的極限狀態(tài)函數(shù)進(jìn)行了模擬，并根據(jù)模擬值確定了它們之間的相關(guān)系數(shù)。

由于常見的隨機(jī)變量，這些失效模式是相互關(guān)聯(lián)的。圖5顯示了不同破壞模式隨時間的相關(guān)性變化。值得注意的是，由于所使用的隨機(jī)變量是相同的，這2種破裂破壞模式是完全相關(guān)的。

基于所有失效模式的系統(tǒng)失效概率有或沒有相關(guān)性使用方程式。式（29）和式（28）分別繪制在圖6中，對應(yīng)于每個單獨(dú)失效模式的失效概率。可以看出，如果不考慮失效模式之間的相關(guān)性，系統(tǒng)失效的概率會被大大高估。這證明了在確定具有多種失效模式的受腐蝕鋼管的系統(tǒng)失效概率時，需要考慮不同失效模式之間的相關(guān)性。

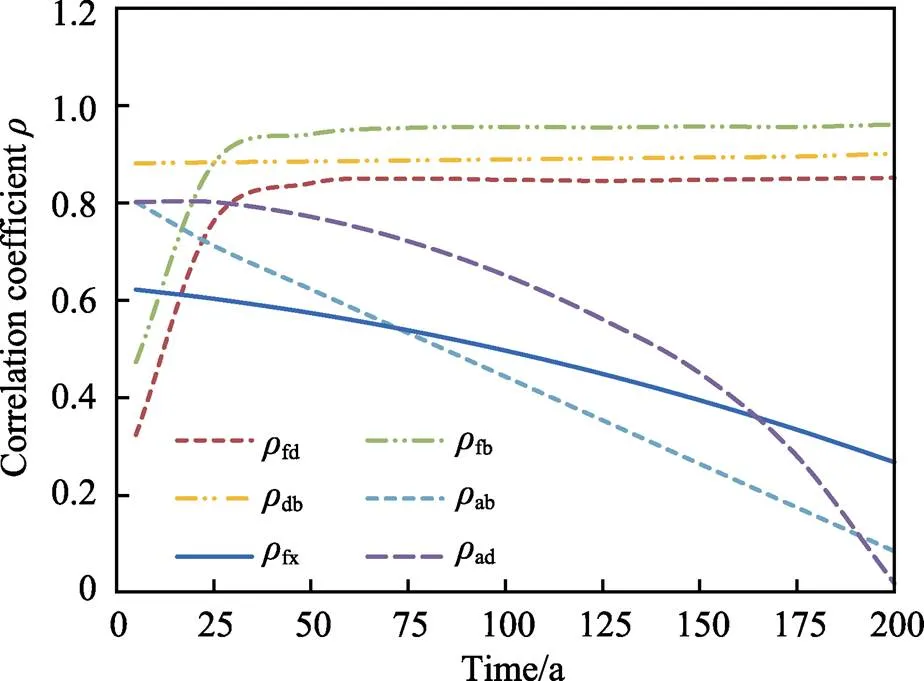
圖5 不同失效模式之間的相關(guān)性

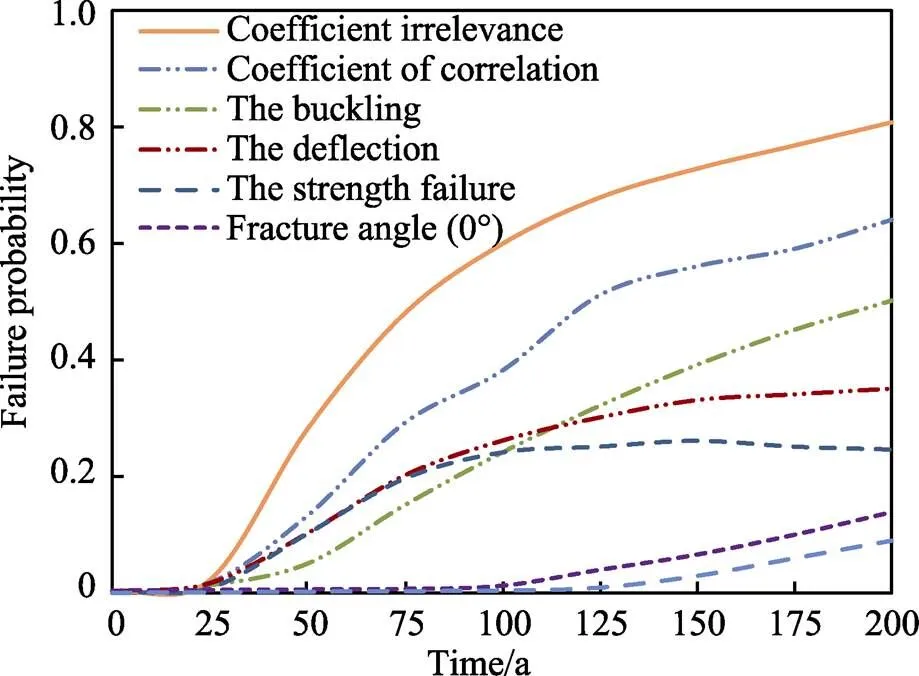
圖6 每種失效模式的失效概率和系統(tǒng)之間存在或不存在相關(guān)性的概率

4.2 敏感性分析

隨機(jī)變量的統(tǒng)計(jì)量是可靠性分析的基礎(chǔ)。由于一些隨機(jī)變量缺乏完整的統(tǒng)計(jì)數(shù)據(jù)，需要進(jìn)行敏感性分析，找出最具影響力的隨機(jī)變量，以便對這些變量的隨機(jī)性進(jìn)行進(jìn)一步的研究。在本文中，使用Nowak和Collins提出的概率靈敏度指數(shù)來證明每個隨機(jī)變量對所有失效模式的失效概率的貢獻(xiàn)。概率靈敏度指數(shù)[22]可表示為：

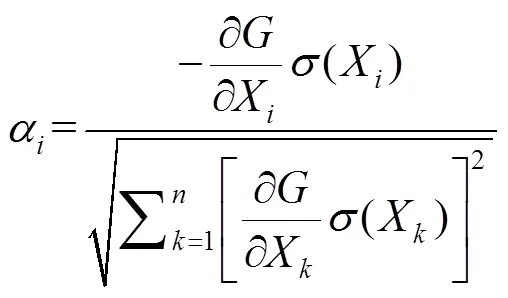
式中：X為隨機(jī)變量（= 1, 2, …,），為設(shè)計(jì)變量個數(shù)，(x)為隨機(jī)變量X的標(biāo)準(zhǔn)差。根據(jù)表1所示的統(tǒng)計(jì)信息，計(jì)算并繪制出傾斜角為30°時，裂縫的不同隨機(jī)變量的概率敏感性指數(shù)，如圖7a所示。當(dāng)傾角為0°時也有類似的變化趨勢。對于埋地管道破裂，在5個隨機(jī)變量中，只有管道厚度指數(shù)為負(fù)，其他變量為正，說明管道破裂的概率隨著指數(shù)為正的變量的增加而增加，反之亦然。一般來說，在整個管道使用壽命中，只有系數(shù)對失效概率的貢獻(xiàn)大小持續(xù)增加，而其他系數(shù)的貢獻(xiàn)大小則不斷減小。

強(qiáng)度、撓度和屈曲的概率靈敏度指數(shù)見圖7b—d。對于強(qiáng)度破壞，如圖7b所示，只有管壁厚度指數(shù)為負(fù)，其他均為正，這一點(diǎn)類似于斷裂。在這15個變量中，乘常數(shù)、指數(shù)常數(shù)、內(nèi)半徑i、內(nèi)壓和管厚對強(qiáng)度破壞概率的影響較大，其他變量對強(qiáng)度破壞概率的影響可以忽略不計(jì)。對于屈曲和撓度，除管材厚度外，鋼的楊氏模量和土的反力模量均為負(fù)值，其余均為正值（圖7c、圖7d）。在所有變量中，腐蝕模型中的乘數(shù)常數(shù)、指數(shù)常數(shù)和管厚對失效概率的影響較大，分別為正指數(shù)和負(fù)指數(shù)。腐蝕模型系數(shù)和產(chǎn)生的影響較為顯著，這一點(diǎn)也與實(shí)際經(jīng)驗(yàn)相符。對于管道的厚度，已知對于給定的管道直徑，值越大，管道強(qiáng)度越大，失效概率越小。

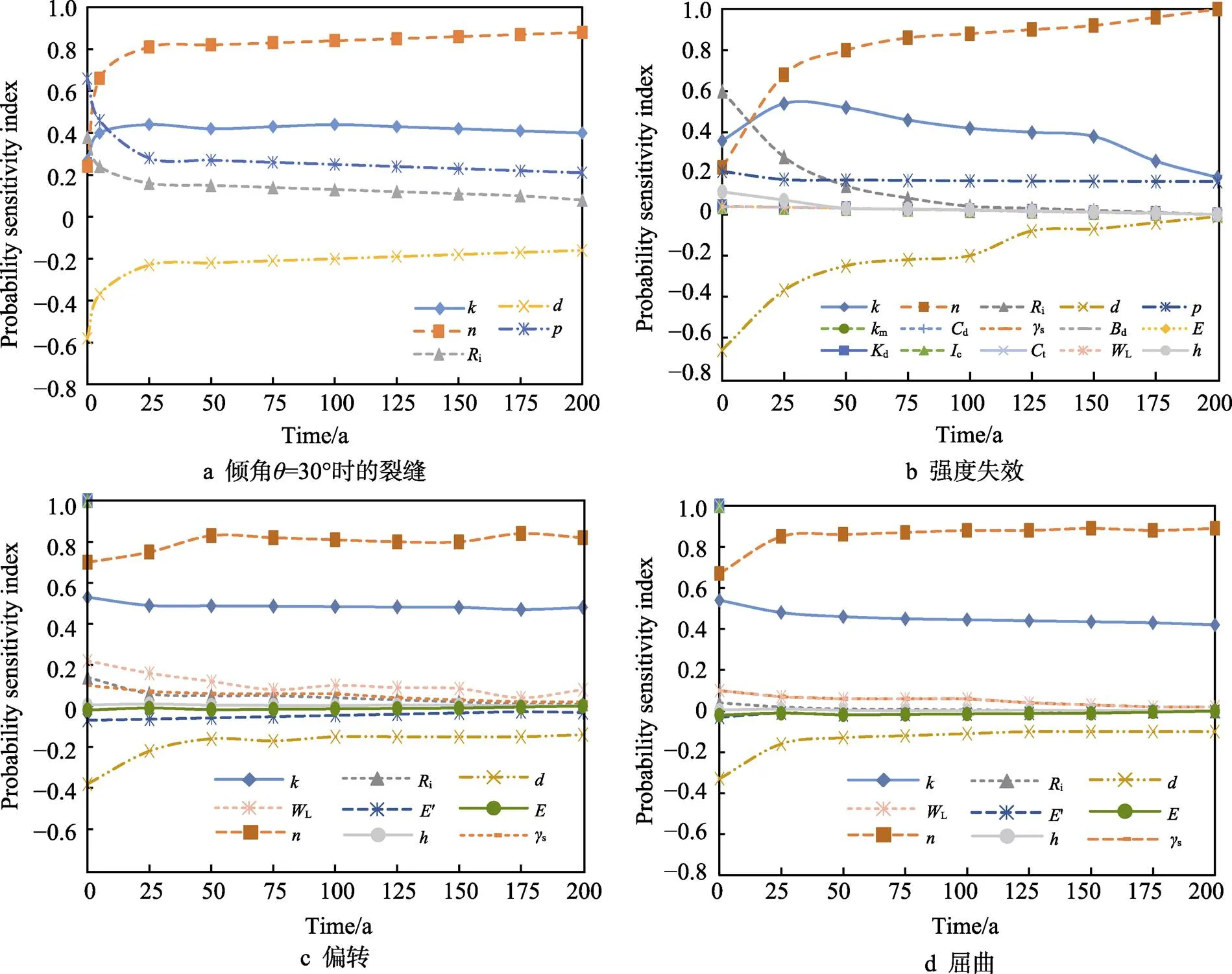
圖7 概率靈敏度指數(shù)隨時間的變化

概率靈敏度指數(shù)隨時間的變化，從而得到了與時間相關(guān)的腐蝕管道損傷概率模型，得出了不同年限下腐蝕管道的概率靈敏度指數(shù)。研究結(jié)果顯示，傾角、強(qiáng)度、撓度和屈曲的概率靈敏度指數(shù)徑向腐蝕速率的分散性對管道失效概率具有雙向擾動作用，其機(jī)理在于隨機(jī)變量的分散性和腐蝕速率同時影響失效概率的波動，開始階段隨機(jī)變量分散性起主導(dǎo)作用，兩者在管道失效概率達(dá)到一定程度會趨于一個平衡狀態(tài)，之后腐蝕速率起主要支配作用。另外，管材的抗拉強(qiáng)度對腐蝕管道失效概率的影響較屈服強(qiáng)度的影響更大，可靠性分析時采用只考慮屈服強(qiáng)度的強(qiáng)度模型將存在一定的局限性，建議同時考慮管材抗拉強(qiáng)度的影響。

5 結(jié)論

1）不同時間點(diǎn)的過程相關(guān)性對每種失效模式的失效概率有較大的影響。管道幾何形狀、腐蝕速率、水壓等，在不同時間點(diǎn)是相互關(guān)聯(lián)的，以致載荷效應(yīng)在時域上相互關(guān)聯(lián)，從而影響腐蝕過程。

2）不同失效模式之間的相關(guān)性對系統(tǒng)失效概率估算結(jié)果具有較大的影響。不考慮失效模式相關(guān)性的埋地管道失效概率估算結(jié)果相比于考慮相關(guān)性的估算結(jié)果偏高。

3）腐蝕模型中的乘數(shù)常數(shù)、指數(shù)常數(shù)和管厚對失效概率的影響較大。和對失效概率的概率靈敏度指數(shù)為正值，與失效概率間的概率靈敏度指數(shù)為負(fù)值。隨管道使用年限的增加，與有增大的趨勢，值的上限在不同的失效模式下均可達(dá)到0.8以上，則可增至?0.2以上。同時，逐年減小，其最低值可降至0.2左右。上述規(guī)律對不同的失效模式均適用。

[1] 張鵬, 彭?xiàng)? 考慮隨機(jī)變量相關(guān)性的腐蝕管道失效概率[J]. 石油學(xué)報(bào), 2016, 37(10): 1293-1301.

ZHANG Peng, PENG Yang. Failure Probability of Corro-ded Pipeline Considering Random Variables Correla-tion[J]. Acta Petrolei Sinica, 2016, 37(10): 1293-1301.

[2] 張杰, 張佩穎, 虞維超, 等. 引入失效數(shù)據(jù)的腐蝕管道結(jié)構(gòu)可靠性評價方法[J]. 安全與環(huán)境工程, 2020, 27(3): 185-192.

ZHANG Jie, ZHANG Pei-ying, YU Wei-chao, et al. Stru-c-tural Reliability Evaluation Method of Corroded Pipel-ines with Failure Data[J]. Safety and Environmental Engi-neer-ing, 2020, 27(3): 185-192.

[3] 帥健, 許葵. 腐蝕管線失效概率的評定方法[J]. 石油學(xué)報(bào), 2003, 24(4): 86-89.

SHUAI Jian, XU Kui. Assessment Method for Failure Probability of Corroded Pipeline[J]. Acta Petrolei Sinica, 2003, 24(4): 86-89.

[4] Ahammed M, Melchers R E. Probabilistic Analysis of Underground Pipelines Subject to Combined Stresses and corrosion[j]. Eng Struct, 1997, 19(12): 988-994.

[5] De Silva D, Moglia M, Davis P, et al. Condition Assessment to Estimate Failure Rates in Buried Metallic Pipelines[j]. J Water Supply Res Technol, 2006, 55(3): 179-191.

[6] MELCHERS R E. The Effect of Corrosion on the Stru-ctural Reliability of Steel Offshore Structures[J]. Corr-osion Science, 2005, 47(10): 2391-2410.

[7] AWWA. Steel Pipe - A Guide for Design and Installation - Manual of Water Supply Practices[m]. Colorado: Amer-ican Water Works Association, 2004.

[8] LI Q, SUN C, HUANG Z, et al. Reliability Analysis of Lan Chengyu Corroded Pipeline with Associated Defects[J]. Petroleum, 2015(1): 244-250.

[9] YU Xu-chao, LIANG Wei, ZHANG Lai-bin, et al. Dual- Tree Complex Wavelet Transform and SVD Based Aco-ustic Noise Reduction and Its Application in Leak Dete-ction for Natural Gas Pipeline[J]. Mechanical Systems and Signal Processing, 2016, 72-73: 266-285.

[10] FU Guo-yang, YANG Wei, LI Chun-qing. Stress Intensity Factors for Mixed Mode Fracture Induced by Inclined Cracks in Pipes under Axial Tension and Bending[J]. Theoretical and Applied Fracture Mechanics, 2017, 89: 100-109.

[11] ABDULLA M B, HERZALLAH R. Probabilistic Mul-tiple Model Neural Network Based Leak Detection System: Experimental Study[J]. Journal of Loss Preve-ntion in the Process Industries, 2015, 36: 30-38.

[12] VOIGT C, STORM J, ABENDROTH M, et al. The Influ-ence of the Measurement Parameters on the Crushing Strength of Reticulated Ceramic Foams[J]. J Mater Res, 2013, 28: 2288-2299.

[13] 封子艷, 南蓓蓓, 楊志剛, 等. 不同尺寸雙腐蝕缺陷管道剩余強(qiáng)度研究[J]. 油氣田環(huán)境保護(hù), 2015, 25(3): 4-8, 72.

FENG Zi-yan, NAN Bei-bei, YANG Zhi-gang, et al. The Study on the Residual Strength of the Pipeline with Double Corrosion Defects in Different Sizes[J]. Environ-mental Protection of Oil & Gas Fields, 2015, 25(3): 4-8, 72.

[14] LAYOUNI M, HAMDI M S, TAHAR S. Detection and Sizing of Metal-Loss Defects in Oil and Gas Pipelines Using Pattern-Adapted Wavelets and Machine Learn-ing[J]. Appl Soft Comput, 2017, 52: 247-261.

[15] RAJABIPOUR A, MELCHERS R E. A Numerical Study of Damage Caused by Combined Pitting Corrosion and Axial Stress in Steel Pipes[J]. Corros Sci, 2013, 76: 292-301.

[16] LIN Y C, DENG J, JIANG Y, et al. Effects of Initial δ Phase on Hot Tensile Deformation Behaviors and Fracture Characteristics of a Typical Ni-Based Superalloy[J]. Mat-e-rials Design, 2014, 55: 949-957.

[17] TEE K F, PESINIS K. Reliability Prediction for Corro-ding Natural Gas Pipelines[J]. Tunnelling and Under-ground Space Technology, 2017, 65: 91-105.

[18] 王勇, 李洋, 孫世斌, 等. 腐蝕缺陷管道剩余強(qiáng)度ANSYS有限元模擬可行性研究[J]. 兵器材料科學(xué)與工程, 2014, 37(3): 12-16.

WANG Yong, LI Yang, SUN Shi-bin, et al. Feasibility of Finite Element Analysis on Residual Strength of Pipeline with Corrosion Defects[J]. Ordnance Material Science and Engineering, 2014, 37(3): 12-16.

[19] CHEN Zhong, ZHAO Lian-wen. Application of Small and Medium Wave Analysis for Signal Singularity Detec-tion[J]. Journal of Chongqing Normal University, 2004, 21(2): 15-17

[20] Fu G Y, Yang W, Li C Q. Stress Intensity Factors for Mixed Mode Fracture Induced by Inclined Cracks in Pipes under Axial Tension and Bending[j]. Theor Appl Fract Mech, 2017, 89: 100-109.

[21] 張日向, 顧孜昌, 姜萌. 考慮雙腐蝕缺陷影響的內(nèi)壓鋼管有限元分析[J]. 鋼結(jié)構(gòu), 2010, 25(2): 79-81.

ZHANG Ri-xiang, GU Zi-chang, JIANG Meng. Finite Element Analysis on Pressured Pipeline with Double Cor-r--osion Defects[J]. Steel Construction, 2010, 25(2): 79-81.

[22] 張曉, 帥健. 基于FITNET FFS模型的腐蝕管道失效概率敏感性分析[J]. 中國安全生產(chǎn)科學(xué)技術(shù), 2018, 14(8): 80-85.

ZHANG Xiao, SHUAI Jian. Sensitivity Analysis on Fai-lure Probability of Corroded Pipeline Based on FITNET FFS Model[J]. Journal of Safety Science and Technology, 2018, 14(8): 80-85.

Reliability Analysis of Corrosion Affected Underground Steel Pipes Considering Multiple Failure Modes and Their Stochastic Correlations

,,,

(School of Management, Xi'an University of Architecture and Technology, Xi'an 710055, China)

This paper presents a methodology for determining the probability of system failure of corrosion affected steel pipelines with multiple failure modes, considering the correlation of the load effect process at different time points and the correlation between different failure modes. The failure modes included fracture, strength failure, deflection and buckling and they were all random process and correlations. The first passage probability theory was employed to quantify the probability of pipe failure.The Monte Carlo simulation calculated the mean function()and the standard deviationσ() loading effect at each time point, and the correlation matrix contained the correlation coefficients between the different failure modes as a function of time, and calculated the failure probability of each failure mode, and then determined the failure probability of the system by considering the correlation between different failure modes. A case study was presented to illustrate the proposed methodology, followed by a sensitivity analysis to investigate the effects of key random variable son the probability of pipe failure. In many influencing factors, the multiplier constant, the exponential constantand thethickness of the corrosion model had the greatest influence on the failure probability. With the increase of pipeline service life,andtend to increase. The upper limit ofvalue could reach more than 0.8 under different failure modes, andcould increase to more than ?0.2; at the same time,decreased year by year, and its lowest value could be reduced to about 0.2. The reliability algorithm considering time-varying factors is an effective tool for the failure evaluation of buried steel pipes under the influence of corrosion. The failure prediction of buried steel pipes under the action of corrosion and the determination of the autocorrelation coefficient of the load process at the relevant position of the pipeline in the time dimension and the correlation between different failure modes can improve the accuracy of pipeline failure probability prediction.

corrosion; failure mode; reliability; correlation analysis

TG172

A

1001-3660(2022)04-0202-09

10.16490/j.cnki.issn.1001-3660.2022.04.020

2021-04-14；

2021-08-28

2021-04-14；

2021-08-28

國家自然科學(xué)基金（41877527）；陜西省社科基金項(xiàng)目（2018S34）

National Natural Science Foundation of China (41877527); Shaanxi Social Science Fund Project (2018S34)

王曉敏（1983—），女，博士研究生，主要研究方向?yàn)楣艿赖母g速率預(yù)測和油氣管道風(fēng)險(xiǎn)評估。

WANG Xiao-min (1983—), Female, Ph. D., Research focus: pipeline corrosion rate prediction, oil and gas pipeline risk assessment.

駱正山（1969—），男，博士，教授、博士生導(dǎo)師，主要研究方向?yàn)楣艿栏g速率預(yù)測和油氣管道風(fēng)險(xiǎn)評估。

LUO Zheng-shan (1969—), Male, Doctor, Professor, Ph. D. supervisor, Research focus: pipeline corrosion rate prediction, oil and gas pipeline risk assessment.

王曉敏, 駱正山, 高懿瓊, 等.基于多種失效模式及其隨機(jī)相關(guān)性的地下管道腐蝕可靠性分析[J]. 表面技術(shù), 2022, 51(4): 202-210.

WANG Xiao-min, LUO Zheng-shan, GAO Yi-qiong, et al. Reliability Analysis of Corrosion Affected Underground Steel Pipes Considering Multiple Failure Modes and Their Stochastic Correlations[J]. Surface Technology, 2022, 51(4): 202-210.

責(zé)任編輯：萬長清