站在學生角度 突破思維障礙 解法自然

山東省淄博市周村區實驗中學 王立功

幾何證明問題，是學生感到困惑的問題類型之一。尤其是對于圖形比較復雜的問題，學生常常出現思維障礙，找不到解決問題的方法。作為教師可以實現一題多解，學生一法難求。而當教師將方法講給學生后，學生的收益往往甚微，再次遇到類似題目仍無法獨立解決。教師沒有達到“授之以漁”的目的。因此作為教師更應該站在學生的角度去思考和分析學生的思維障礙，引導和幫助學生從突破自身思維障礙出發，正確找出解決問題的方法。

下文筆者通過一個有代表性的一道幾何問題，詳細闡述如何從學生角度分析問題，解決思維障礙，最后得出多種解決問題的策略的思考過程，希望對讀者有所幫助。

一、例題呈現

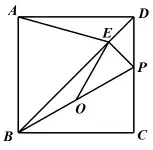
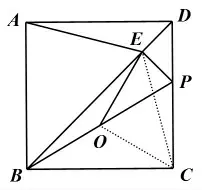
如圖，在正方形ABCD中，點P是CD邊上的動點，連接BP，點O為BP的中點，過點P作PE⊥BD，垂足為E。 連接EO，AE，猜想線段BP與AE之間的數量關系，并證明。

二、學生的思維障礙

1.題目的結論未知，僅通過直觀觀察看不出它們之間的數量關系；點P是一個動點，通過點P的運動，線段BP和AE都在變化，長度不是定值，學生感覺無從下手。

2. 題目中沒有數據可以運用，BP和AE的長度無法求出。

3.BP和AE沒有在同一個直角三角形中，所以通常三角函數等知識無法解決。

4.感覺BP和AE長度不相等，無法運用全等三角形解決。

三、站在學生角度，解決思維障礙，探索解決問題的方法

1.學生思維障礙一：結論未知，看不出兩條線段是什么數量關系。

作為教師如果直接給出學生答案，或者直接利用證明的方式給學生講解，最后得出結論對學生來說是收獲甚微的。不利于學生思維的培養。因此教師可以站在學生的角度思考問題，如果看不出兩者的數量關系可以從什么地方入手來思考。課堂上可以提問學生：“自己的困難在哪？”部分學生會回答：“看不出它們之間的數量關系。”教師順勢再問“為什么看不出來？”“因為點P是動點，長度不確定。”“那么你能感覺它們的關系是確定的嗎？”“一定是確定的。”“那么與點P的位置有關嗎？”“無關。”這時便有學生可以聯想到未知問題的探索可以從猜測開始，而且對于動點問題可以通過特殊位置作出猜測，而特殊位置往往取運動的起始端和末端。當點P運動到點C時，點O運動到BC的中點處。點E恰好是正方形對角線AC與BD的交點，則容易算出；當點P運動到點D時，則點E恰好與D重合，此時容易算出故有不完全歸納法可以猜測出BP與AE的關系為BP=

2.學生思維障礙二：BP和AE長度不相等，無法運用全等三角形解決。

這種思維障礙是學生的思維狹窄，僅僅把線段關系理解為是否相等。因此教師應引導學生思考：兩條線段除了在全等三角形中的相等關系，還會出現不等關系。即一條線段是另一條線段的倍數（或幾分之幾）。這樣就可以引導學生思考如何解決不在一起的兩條線段倍數問題。因此從學生思維的角度很容易得到可以證明兩條線段所在的三角形相似，然后把目標線段之比轉化成兩條已知的線段之比。于是可以有下面的證明方法：

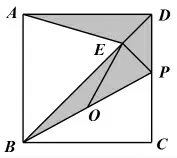
解后反思：構造三角形相似解決兩條線段之比的問題是比較直接的方法。當然也可以通過過點A作AF⊥BD,垂足為點F，利用△AFE∽△BCP來解決。

3.學生思維障礙三：題目中沒有數據可以運用，BP和AE的長度無法求出。

學生這種思維障礙限制在了僅僅運用數字來計算線段長度。為了突破思維障礙教師可以引導學生對于線段的計算除了有數字的代數計算外，還有代數式的運算。因此自然容易得到用設參數的方式表示出所求線段的長度。而對于兩條線段的關系最一般的思路就是通過計算它們的長度進行比較，這樣的解法更為自然。于是可以有下面的解法：

解法2：過點E作EF⊥AD，垂足為F.

設正方形的邊長為a，DP的長為m，則PC=a-m，

在Rt△PBC中，根據勾股定理，

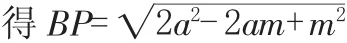
在等腰直角△DEP中，斜邊DP=m，

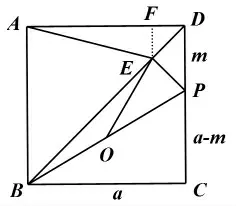
當然對于線段的計算，教師可以進一步引導學生將圖形放置在平面直角坐標系內解決。比如通過以點B為坐標原點，BC所在直線為x軸，以AB所在直線為y軸建立平面直角坐標系。再通過引入參數結合坐標系有關知識來解決類似問題。用代數知識解決幾何問題，這也正是數形結合思想的重要體現。

4.學生思維障礙四：BP 和AE 不在同一個直角三角形中。

解決這個思維障礙就應引導學生思考是否可以想辦法將兩條線段放在同一個三角形中（即兩條線段有公共頂點）。首先想到的便是將其中的一條（或兩條）轉化為與其相等的線段。最終借助第三方線段放在同一個三角形中。通過觀察發現在正方形中AE=EC，而BP=2OE，故只要探索EC和OE的數量關系。因此容易想到連接OC，將上述問題轉化到直角△EOC中。

解法3：連接OC，EC，由四邊形ABCD是正方形，易證AE=CE，因為△BPE和△BCP都是直角三角形，又因為點O是BP的中點，所以BP，設∠EBP=α，則∠OBC=45°-α，∠EOP=α，則∠POC=90°-2α，故∠EOC=90°，由勾股定 理 得：OC2+OE2=EC2，所 以EC2=2OE2，即由BP=2OE，AE=EC，得

思路2：利用正方形對稱性將AE轉化為CE，問題就變成了BP如何轉化到與EC有公共頂點的三角形中。故可以在點E或C處構造與BP相等的線段。因此利用E，B，C，P四點共圓，BP轉化為EF。則由即可以解決。

解法4：連接CE，由四邊形ABCD是正方形，易證AE=CE.因為PE⊥BD，所以∠PEB=90°，因為四邊形ABCD是正方形，所以∠PCB=90°，所以點E，B，C，P四點在以點O為圓心，OE為半徑的圓上，作出該圓，延長EO交⊙O于點F并連接CF，則BP，EF都是圓的直徑，所以BP=EF，因為∠F=∠EBC=45°，所以△ECF是等腰直角

5.學生思維障礙五：部分同學可以探索出BP= AE，但思維障礙是如何構造： AE.

上述思維障礙產生的原因是學生對于直角三角形勾股定理以及三角函數知識點不夠熟悉。教師應該引導學生思考，在什么情況下一個三角形中會出現倍的關系。因此學生很容易想到等腰直角三角形的斜邊與直角邊的比即為。因此可以利用旋轉構造以AE為直角邊的等腰直角三角形，得到然后將BP放在同一個三角形中。解決了這個思維障礙便可以得到如下解法：

解法5：將△ADE繞點A順時針旋轉90°，得到△AFB，連接EF，則△AED≌△AFB，得AE=AF，∠EAF=90°，FB=ED，∠ABF=∠ADE=45°，所以，因為PE⊥BD，∠EDP=45°，所以ED=PE，所以FB=PE，由∠ABD=45°，得∠ABF+∠ABD=90°，所以∠FBD=90°，所以FB∥PE，則四邊形FBPE是平行四邊形，所以BP=EF，因為

當然也可以將AE繞點A逆時針旋轉90°，構造以AE為直角邊的等腰直角三角形，得到

解后反思：直接告訴學生本題可以運用旋轉變換來解決，對學生來說是有一定困難的。而通過解決學生思維障礙的角度看，構造等腰直角△FAE便會順其自然。其本質也就是旋轉。當然按照上述思路還可以先得到AE=EC，然后構造BP=

當然部分同學會想到AE=EC，仍然是存在思維障礙：如何構造因此可以類似上面解法，通過旋轉構造以EC為直角邊的等腰直角三角形。

四、反思

1.教師要放手讓學生自己尋找解決思維障礙的方法。

傳統的數學教學教師常常以自己為中心，不顧學生的實際情況，察覺不到學生的思維困難，而是任由教師按照自己的思路或知識邏輯灌輸式教學。這也就導致教師講解完例題之后學生真正掌握的非常少。學生沒有把教師所講的知識內化為自己的知識。所以當學生自己去解決問題時往往感到無所適從。學生遇到一個或多個思維障礙無法克服，長此以往便形成了學生思維的膚淺性和數學思維的消極性。因此教學中不能僅僅讓優秀生完美地展示他們的過程，更應該鼓勵解題有困難的同學暴露他們的思維障礙，通過解決思維障礙，引領他們思維的深度和廣度，逐步培養學生的思維能力。前蘇聯教育家維果茨基曾提出兒童最近發展區理論。而學生思考問題的每一個思維障礙便是學生已有水平與將要解決的問題的差距。從學生思維的現有角度去思考和解決問題符合學生的發展規律。葉瀾教授曾指出：“課堂教學中，教師應積極地看，積極地聽，設身處地地感受學生的所作所為、所思所想，積極鼓勵學生質疑問難，允許出錯，允許改正”。教學中多鼓勵學生多換一個角度想問題，勤問一下有困難的學生思考到了哪一步，你還需要哪些條件，你做了哪些嘗試，等等。因此課堂教學中教師要站在學生的角度，教給學生克服思維障礙的方法才會讓學生形成良好的解題習慣，真正提升學生的數學素養。

2. 解決思維障礙有助于實現一題多解，能夠提煉通性通法。

幾何證明題重在培養學生邏輯思維能力和分析問題的能力。一題多解就需要學生認真分析條件和結論，大致可以從哪幾個大的方面去思考。每一條思路遇到思維障礙要及時變通，思考如何解決，遇到瓶頸更要學會有沒有其他路線可以運用。打通每一個思路便是一種好的解題方法。當然教學中應當讓學生去總結遇到類似的問題一般從哪些方面去解決，這就是通性通法。通性通法的總結和提升應當是學生在教師的引導下來總結，更多的是學生的思考，而不是教師的灌輸。通性通法的總結有助于幫助學生解決學生思維障礙，實現高效解題。因此日常教學要教會學生通過解題反思自己的思維障礙，并以此總結通性通法。

3.以生為本，尊重學生的認知規律，課堂教學積極應對學生的思維障礙。

教學中教師要想了解到學生的思維障礙就應從學生的學習實際出發，了解到每一名學生存在的思維障礙。比如小組合作盡量不要讓優秀的同學講解自己獨到的方法，讓他們成為一言堂。而更應該利用學習小組鼓勵思維有困難的同學先講解自己的思路，暴露自己的思維障礙，然后由同學或老師幫助解決。這樣的合作才更有效。組長對本組內每一名學生的思維障礙反饋給教師，教師根據學情有針對性的講解，打通每一名同學的思維障礙，這才是真正的以學定教，這樣的課堂才更有實效性。

4.鼓勵學生有克服困難的信心。

對于幾何問題的教學，應鼓勵學生敢于應對困難，提升自己思維的敏捷性。遇到思維障礙導致思路停滯不前時，善于尋找突破思維障礙的關鍵因素。對題目的已知條件和隱含條件重新梳理，對自己的思考方向尋找突破口。鼓勵學生善于變換角度思考問題，拓寬自己的思維視角。當然對于一個幾何問題的解決不一定有多種證明方法，但是當學生具備了能夠突破自己思維障礙的思維品質時，自己的解題能力會有較大提升。對于教師的教學來說，應該做到以生為本，真正落實學生的主體地位。教學中將自己的思維“放低”，站在學生的立場思考問題，和學生一起思考解決問題的方法。善于運用“臺階式”的問題啟發學生的思維，逐步克服學生的思維障礙，實現高效的數學課堂。