基于小麥收割機作業路線行走方向的調度優化研究*

南風，曹光喬，李亦白，陳聰，劉東

(農業農村部南京農業機械化研究所，南京市，210014)

0 引言

農機調度已經在農業領域中得到廣泛的使用，例如收割機跨區收獲、無人機植保作業、農作物測繪、監測以及收割機與運糧車響應等農業作業環節[1]。農業機械的作業路徑很大程度上決定作業過程的質量、效率和成本消耗[2]，因此農業設備作業路徑的規劃和優化工作具有重要意義。隨著人工智能技術的不斷發展，國內外農業正在經歷一個重要的轉折點：傳統農業的耕作過程正在逐步轉變為一種全新智能視角下的作業方式[3]。其中國外相關研究內容較多，但更多針對大型農場與大型地塊的農業機械調度問題，由于我國的“大國小農”國情，因此在國內現階段的推廣應用較少且適用性較差[4-5]。目前全覆蓋路徑規劃問題在國內農業領域的相關研究處于起步階段：一方面集中在植保無人機的飛行航跡規劃上；另一方面關于地面農機的路徑規劃問題集中在聯合收割機在多個區域的轉移路徑上[6-8]，并不屬于同一區域的全覆蓋作業問題。徐博等[9-11]對多邊形邊界單田塊的無人機作業路徑提出了具體的算法并對多區域路徑轉移進行了研究。王宇等[12]對無人機作業提出了一種基于柵格模型的路徑規劃算法。黃小毛等[2]基于復雜邊界田塊對無人機自主作業路徑進行了研究。總體來看，關于農機作業區域全覆蓋路徑規劃相關文獻仍然較少，而且地面與空中農業設備相比[13]，地面農機的作業不具備無人機的速度、通過性強等特點，地面農機全覆蓋作業要時刻受到作業環境、少重復及遺漏面積等條件的制約，因此植保無人機路徑規劃方法雖然可以借鑒，但仍然需要考慮適合眾多地面環境、設備本身參數及具體作業流程的影響。

對于重要的小麥收獲作業環節，聯合收割機通常在規則農田區域內沿著邊界長邊方向進行收獲作業[14]。小麥播種時，大面積的農田通常采用機械直播(條播)方式，中小面積通常還是人工均勻播撒，分布較為集中且均勻，因此對于不規則形狀地塊或受環境因素制約的不規則地塊，可以采用優化行駛方向使小麥收割機轉彎次數最少。該場景下的收割機全覆蓋作業路徑優化對于不規則農田的小麥播種、水稻播種、全覆蓋深耕等全覆蓋作業路徑規劃問題都具有一定的借鑒和推廣價值。

本文擬針對小麥收獲環節聯合收割機作業時可能遇到的復雜類型田塊問題，提出一種基于作業優化方向的全覆蓋路徑規劃算法，以獲得凸邊形、凹邊形等多邊形邊界地塊的作業路徑軌跡，為實際環境下復雜邊界地塊的農機全覆蓋路徑規劃提供借鑒和理論支持。

1 優化轉彎次數的全覆蓋調度

小麥聯合收割機田間收獲作業路徑規劃應該滿足以下要求：有效工作路徑中達到農田所有區域的全覆蓋，重復作業及遺漏作業面積盡可能小；聯合收割機轉彎次數盡可能少。

傳統的收割機田內覆蓋收獲作業方式較為適合標準、規整的矩形農田區域，通常表現為沿固定方向往復行走，該行走方向平行于區域最長邊界，又被稱為牛耕往復法，能夠取得最少的轉彎次數。而對于不規則形狀的農田區域(非平行四邊形)，行走路線無法與區域大多數邊界平行或垂直，總存在一定的角度，因此會出現收割機轉彎次數較多的現象。

對于一般小麥收獲作業環節，聯合收割機在規則農田區域內，沿區域邊界的最長邊方向進行作業。但對于不規則邊界地塊，當收割機基于不同方向進行作業時，由于割幅相同、作業面積固定，整體行走的有效路徑長度是一定的，但是各方向受場地形狀與邊界限制，轉彎次數發生改變，在田內轉彎次數增多則會造成耕作面積遺漏的風險，收割效率降低。因此基于不規則多邊形農田區域的調度模型，需要優化不同收獲方向使收割機轉彎次數最少。同時由于國內收割機通常轉彎在田塊內部，不必考慮收割機在田外的重復和多余覆蓋面積，因此行走方向不同直接影響了收割機的轉彎次數，且轉彎過程總是伴隨著收割機的減速和加速過程，增加作業時間和油耗。可以得出：在收獲環節收割機的行走方向能夠影響轉彎次數從而增加收獲作業的成本，因此需盡可能減少轉彎次數，對田間收獲作業過程中收割機行走方向進行優化。

該場景的收割機調度優化對于不規則農田的小麥播種、水稻播種、全覆蓋深耕等環節的全覆蓋作業路徑場景都具有一定的適用性，能夠提高農機作業效率，降低農機油耗。收割機田內作業路徑規劃適合于所有復雜邊界地塊，無論是農田面積大小都能得到應用，大型農田的復雜邊界地塊優化效果更加明顯。實際情況下，小麥聯合收割機收獲作業中會出現卸糧過程以及收割機在不同農田的田外轉移過程，但上述環節并不影響收割機單獨田塊的轉彎次數，因此為了簡化處理過程，本研究不考慮收割機卸糧和往返農田的非工作時間、不考慮收割機配置參數等無關因素，固定割幅同時僅探究不同行走方向對轉彎次數的影響。

因此小麥聯合收割機田內作業場景可以描述為：當一臺收割機采用牛耕往復法進行全覆蓋收獲作業時，在不規則區域內尋找最優路徑方案使轉彎次數最少，提高收割效率、降低作業成本。

2 基于牛耕往復的調度規劃模型

本文針對常見的二維田塊，對于規則形狀農田(如矩形農田)，常用的區域覆蓋作業方式主要是牛耕往復法和內外螺旋法，相關文獻[9-11]已經證實采用內外螺旋法會造成重復覆蓋和遺漏覆蓋的現象，與牛耕往復法轉彎次數相同，因此規則矩形采用牛耕往復方式進行聯合收割機收獲作業更為合適。牛耕往復法如圖1所示。

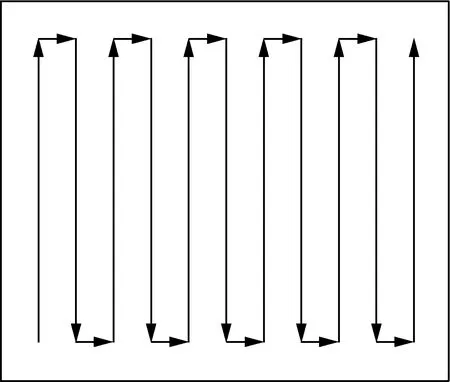
圖1 規則區域的牛耕往復法Fig. 1 Full coverage method for a regular region

當作業區域為規則矩形，沿著區域一邊每隔二分之一割幅繪制掃描線，掃描線方向的參考線為矩形農田長邊，從左向右排序，實線為收割機作業路徑，箭頭表示行走方向，可以快速獲得牛耕往復法的作業路徑，此時由于是規則矩形，收割機沿長邊行走距離達到最大值，因此所需轉彎次數最少，行走路徑最優。當作業區域為不規則多邊形時，利用簡單圖形幾何關系無法精確滿足路徑規劃的要求，因此本研究利用掃描線法獲得農田路徑信息，結合改進的角度尋優算法進行作業路徑的規劃。首先由GIS軟件提取作業區域的地圖信息，提取作業農田邊界點經緯度，構建二維平面坐標地圖，繪制包裹整個作業農田且長款均為收割機割幅整數倍的矩形。對于收割機作業而言，用一組方向相同、間距與收割機割臺寬度相等的掃描線進行掃描，掃描線與閉合多邊形的邊界交點所形成的線段就即為收割機路徑集合。根據地塊形狀和農機路徑規劃情況的分析，可將指定作業區域收割機作業路徑規劃等價于多邊形區域與掃描線交點問題。

對于不規則多邊形，待作業區域為凹邊形或凸邊形農田，農田面積為S，收割機收割幅寬為d，收割機基于行走方向為θ時的行走路徑設置為集合L，路徑個數為n，其中第i條直線路徑設置為li，i=1，2，…，n。設置農田多邊形邊界與掃描線(即收割機工作路徑)交點個數記為路徑節點N，則可以計算出掃描線個數為交點個數的一半即N/2。

該模型目標數學表達式

Z=min(fθ(N/2-1))，?θ∈(0°，360°)

(1)

式中：fθ(N/2-1)——行走方向θ時，收割機工作路徑的轉彎次數最小值。

約束條件

(2)

式(2)表明收割機總路徑長度與割幅寬度的乘積，即最小覆蓋面積要大于農田面積。

理論表明：當收割機每次行走路線上割幅相鄰且不重合時即農田面積覆蓋不重復且不遺漏，由于農田總面積固定，因此收割機的有效行駛路徑長度是固定的。因此，本研究基于以下假設建立收割機路徑規劃模型：(1)不考慮作業農田的多收割機調度及田內障礙物；(2)收割機兩個相鄰路線中無農田遺漏面積及重復覆蓋面積；(3)收割機始終按照牛耕往復法行駛，并保持同一工作方向，不考慮其他的轉彎類型。

3 轉彎次數求解及角度優化算法

3.1 轉彎次數求解算法

3.1.1 凸多邊形掃描線算法

掃描線法又稱為有序邊表法，是用于表征和求解地塊數據集和位置信息的算法，是計算機圖形學中的經典問題，在計算機動畫、3D打印和機器人路徑規劃等領域均有運用。掃描線法能夠提高對每一組線段相交信息的求解效率和速度，因此可以用于收割機牛耕往復法的作業情景。

可以將不規則農田區域的經緯度坐標轉換為二維平面坐標系下的閉合多邊形區域[15]，已知不規則多邊形區域的頂點坐標，將掃描線與x軸的夾角θ作為掃描線方向。θ=0°，即若干等間距水平掃描線等價于行走路徑，計算掃描線與多邊形各邊的交點坐標，能夠計算每條路徑的長短，通過統計與多邊形各邊交點個數來計算路徑個數，從而計算轉彎次數。

掃描線算法的最重要特點是，無須計算多邊形所有邊與掃描線的交點，每條掃描線與多邊形相交位置僅僅存在幾條邊；同時相鄰的掃描線由于具有相同間隔，因此對于多邊形同一條邊，所有相交掃描線均有一定的步進關系，可以證明相鄰掃描線的步進量Δx為相交邊所在直線(Ax+By+C=0)斜率的倒數。

Δx=-B/A

(3)

若相鄰掃描線間距不是1而是Δt，則表達式

Δx=-B×Δt/A

(4)

因此，基于掃描線的重要幾何、數量特征，將掃描線與多邊形相交邊集中在一個數據表中，就形成了“有序邊表法”：儲存邊的數據結構，以水平掃描線(方向角為0°)為例，每行信息由數組(Ymax，Xymin，Δx，next)組成，Ymax表示該多邊形邊的縱坐標最大值即該邊上端的Y值；Xymin表示該邊縱坐標最小值對應的橫坐標X值，即該邊下端點X坐標；Δx表示沿該邊方向相鄰掃描線之間的水平增量(X方向增量)，next表示下一條相交邊。建立邊表時，先按照下端點縱坐標值(即從下到上的方向)對多邊形所有邊進行分類，再將同一組的各邊按照下端點橫坐標值進行增量排序，若橫坐標相同，按照Δx大小增量排序。具體實現過程見相關文獻[2]，本節不再贅述。

掃描線算法步驟如圖2所示。

圖2 掃描線算法流程圖Fig. 2 Flow chart of scanning line algorithm

3.1.2 凹多邊形假想區域求解算法

掃描線算法能夠滿足求解復雜凸多邊形邊界的收割機轉彎次數，但是實際環境中，作業農田往往因為周圍水池、樹木、建筑等出現相鄰邊界形成內角大于180°的凹邊形區域。因此本研究在掃描線求解凸多邊形基礎上改進并設計了基于凸邊形填補方法的幾何算法對凹邊形區域進行行走方向的尋優計算。主要步驟如下。

步驟1：依次輸入凹邊形區域S0各邊頂點，并選擇頂角大于180°的區域頂點o兩側相鄰頂點所成假想直線l與除該頂點外凹邊形所有頂點共同組成凸邊形區域S1，同時該直線與該頂點o相鄰兩邊界組成假想三角形區域S2。

步驟2：設置收割機作業參數，以及行走方向θ=0°，旋轉步進量Δθ=1°。

步驟3：使用掃描線算法(參見3.3.1節算法步驟)分別計算行走方向θ時，凸邊形區域S1、S2對應的各邊路徑節點個數n1、n2，同時記錄假想區域S2邊界的直線l節點個數為nl。

步驟4：計算凹邊形區域S0轉彎次數，N(S0)=(n1+n2-2nl)/2-1。

步驟5：令θ=θ+Δθ。

步驟6：當θ>180°時，停止迭代并輸出最小N(S0)對應的θ值。

該假想區域算法的示意如圖3所示。

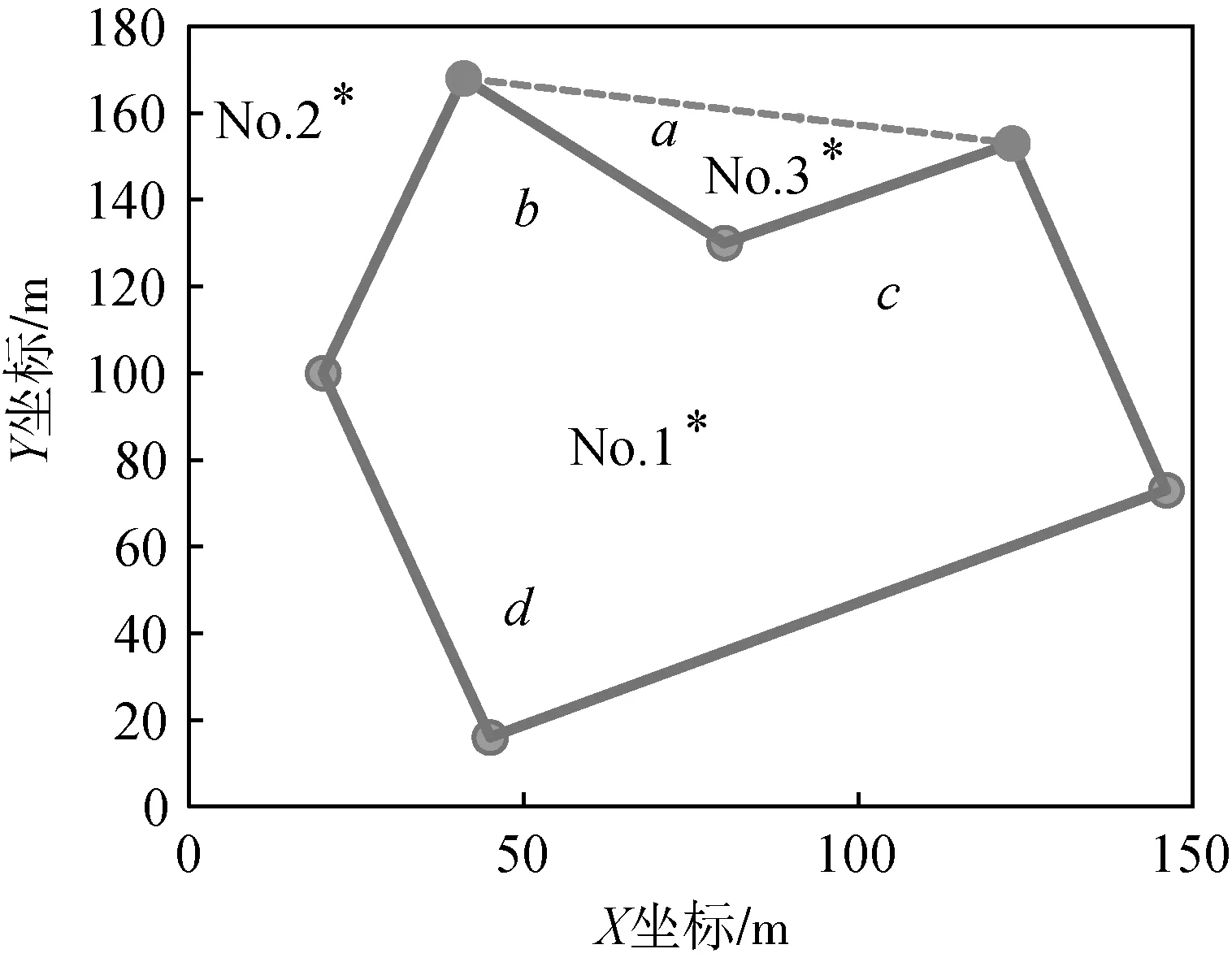
圖3 假想凸邊形區域組成Fig. 3 Composition of farmland in an imaginary convex region

如圖3所示，當不規則區域圖形為凹多邊形時，可以通過填補的形式，將凹邊形的相鄰兩條邊(夾角大于180°)所形成的區域直接用一條假想線連接頂點，從而形成凸邊形區域，因此該凸邊形就由原先凹邊形與假想區域凸邊形組成。原凹邊形由b、c邊以及剩余邊集合d組成，記為多邊形No.1；組合凸邊形由假想線a(圖3中虛線)與邊集合d組成，記為多邊形No.2；假想區域所形成的也是凸邊形，由假想線a、原邊b、c形成，記為多邊形No.3。對于收割機工作路徑來說，轉彎次數與路徑線個數有關，可以通過區域邊與路線交點數量計算得到，這里將多邊形邊與掃描線交點記為路徑節點，數量用N表示，假設區域各邊頂點不存在路徑節點，可以得到

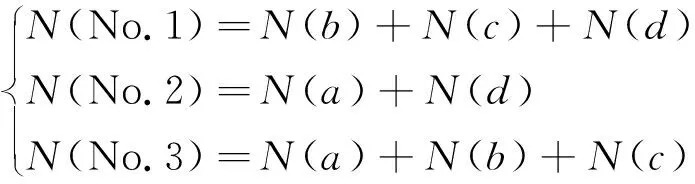
(5)

通過凸多邊形掃描線算法可以得到凸邊形(No.2與No.3)各邊路徑節點數量。因此可以推出原凹變形區域節點數量，得到關于N(No.1)與N(a)的表達式如式(6)所示。

N(No.1)=N(No.3)+N(No.2)-2N(a)

(6)

因此已知原凹邊形邊界信息，形成的假想兩個凸邊形邊界信息通過凸邊形算法求解得到轉彎次數及假想邊界與路徑的相交次數，就可以獲得原凹邊形的轉彎次數。

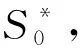
(7)

式中：n——區域所有邊界或指定邊界線上的路徑節點數量。

若實際復雜環境下的農田作業區域可以轉換為不規則凸、凹邊形區域，則通過轉彎次數求解算法可以得到相應結果。

3.2 最優作業角度搜索算法

對單一多邊形田塊而言，可以采用“旋轉法”進行近似求解，本質上屬于窮舉算法，從0°開始，以1°為步長，計算所有可能的行走方向的路徑，比較所有路線的轉彎次數N，取其最小者對應的方向值為最優行走方向。當θ≠0時，通過坐標變化可簡化計算過程，將多邊形頂點繞坐標原點順時針旋轉θ(正變換)得到旋轉后的多邊形頂點，基于掃描線法計算得到中間路徑，再將路徑線端點(x0，y0)繞著矩形原點逆時針旋轉θ(逆變換)即得到真實路徑的端點(x，y)。

正變換

θ=-θ*(互為相反數)

(8)

逆變換

(9)

總體來看，本研究通過旋轉步進搜索算法，再結合多邊形轉彎次數求解算法，便能夠得到基于最優行走方向的復雜多邊形最優路徑軌跡。具體算法步驟如圖4所示。

圖4 算法流程圖Fig. 4 Algorithm flowchart

4 算例驗證

上述全部算法過程在Window10系統環境下編碼實現，在同一工作參數條件下進行多次試驗，測試算法計算尋優結果。本研究利用假想田塊邊界，轉化為二維平面直角坐標，對單一多邊形邊界的田塊采用“旋轉法”優化行走方向。轉彎次數通過計算掃描軌跡線個數得到，掃描線數目通過計算多邊形各邊交點數目(即路徑節點)總和得到。一般小型聯合收割機割臺寬度在1.5～3 m，因此根據常見聯合收割機型號及中小型農田區域面積，本文取收割機的工作寬幅為2.5 m。

4.1 凸多邊形作業路徑優化方案

仿真算例轉換至笛卡爾坐標系中，水平方向與x軸重合，農田邊界信息及頂點坐標如圖5所示，通過凸邊形掃描線算法求解，得到最優作業角度為100°。為驗證算法計算結果，使行走方向與水平方向夾角分別為0°、45°、90°、135°，沿區域最長邊方向29.5°，以及算法得出最優角度100°的凸多邊形區域農田填充掃描線如圖6所示。

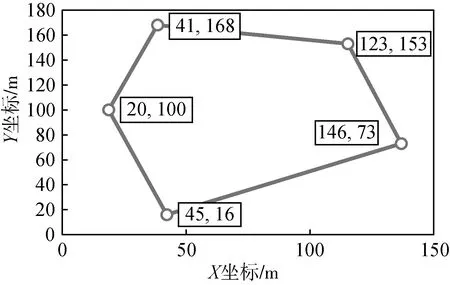
圖5 凸邊形區域農田Fig. 5 Cropland in single area with convex edge

(a) θ=0°

(b) θ=45°

(c) θ=90°

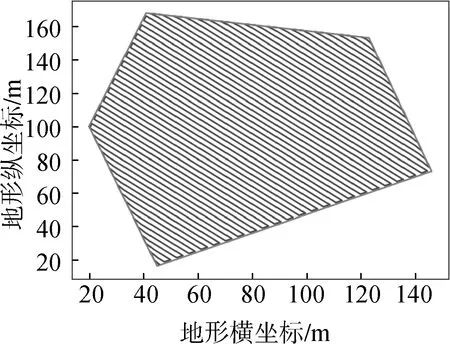
(d) θ=135°

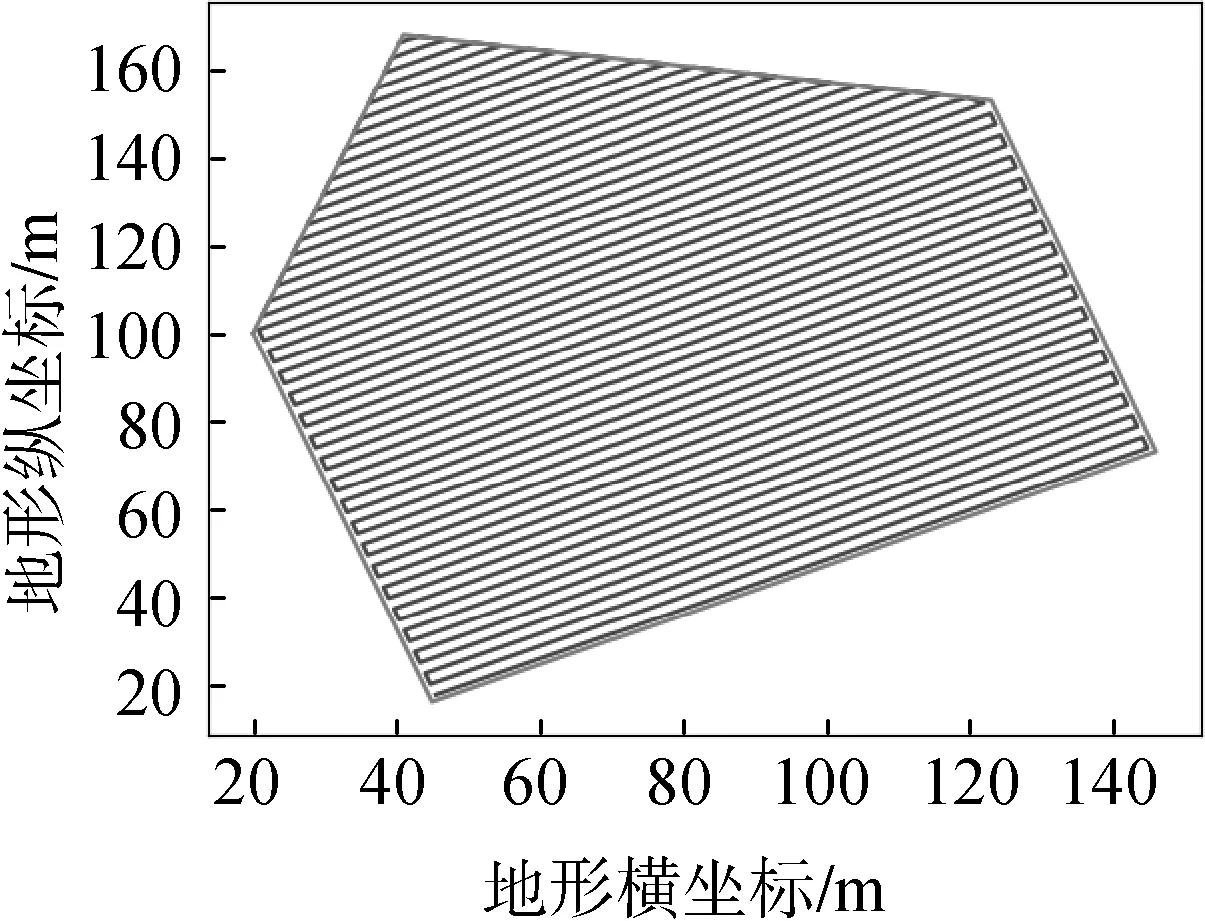
(e) θ=29.5°

(f) θ=100°圖6 凸邊形區域不同行走方向路徑軌跡線Fig. 6 Path trajectories of different operating directions in the convex edge area

當行走方向與水平夾角θ=100°時，該區域田塊的作業方案最佳，作業進入點坐標為(168，41)，作業路徑節點為96個，收割機轉彎次數為47次。指標結果如表1所示：與基于其他方向的作業路徑方案相比，當行走方向θ=100°時，同一收割機比行走方向為0°、135°轉彎次數少13次，優化率達21.67%，比行走方向為45°轉彎次數少9次，優化率達16.07%、比行走方向為90°少3次，優化率為6%、比作業沿長邊方向為29.5°轉彎次數少6次，優化率為11.32%，因此可以得出該算法能夠有效處理基于不同角度尋優的凸多邊形農田的收割機調度規劃，并得出全局最優行走方向。

表1 基于不同角度的凸多邊形農田指標Tab. 1 Indicators of convex polygons based on different operating directions

4.2 凹多邊形田內作業路徑優化方案

凹邊形仿真算例的邊界信息如圖7所示，對凹邊形進行填充的區域已通過圖3表示，其中a為相鄰內角大于180°的邊界(b、c)頂點形成的假想線，d為原凹邊形其余邊界，最長邊與橫軸夾角為29.5°。由第3節凹邊形作業角度優化算法原理可知，關于N(No.1)與N(a)的表達式為N(No.1)=N(No.3)+N(No.2)-2N(a)。

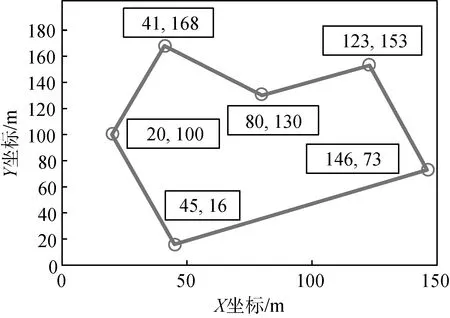
圖7 不規則凹邊形區域農田Fig. 7 Farmland with irregular concave edge area

通過凸多邊形掃描線算法可以得到凸邊形(No.2與No.3)各邊路徑節點數量。N(a)可以通過掃描線算法得到。因此通過算法求解原凹邊形區域填充掃描線，行走方向與水平方向夾角分別為0°、45°、90°、135°，沿區域最長邊方向29.5°，以及算法得出假想凸多邊形區域最優角度100°，如圖8所示。

從圖8可以看出，θ=100°是凸多邊形No.2的最優作業角度，但是對于去掉假想區域(No.3)后的實際凹邊形農田(No.1)來說，θ=100°的轉彎次數要多于45°、90°、29.5°，即凹邊形農田最優作業方向并不能通過填補的假想凸邊形尋優計算直接獲得。因此，依據3.2節的旋轉搜索算法，在Window10系統上設置旋轉步長為1°，旋轉次數為180次，得到0°～180°中轉彎次數最少的行走方向，即最優作業方向。凹邊形農田區域旋轉算法求解過程的收割機轉彎次數如圖9所示。

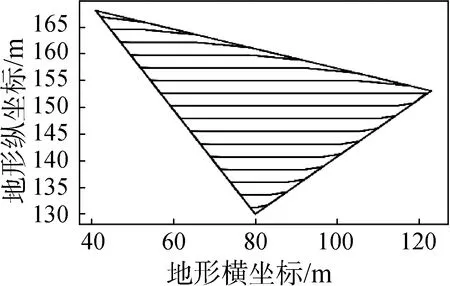
(a) θ=0°

(b) θ=45°

(c) θ=90°

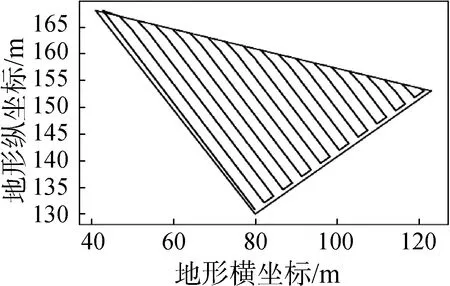
(d) θ=135°

(f) θ=100°圖8 假想區域的掃描線軌跡Fig. 8 Scan line trajectories of imaginary regions

圖9 不同角度下凹多邊形區域的轉彎次數Fig. 9 Number of turns in a concave polygon area with different angles

通過圖9可知，當行走方向為90°時，凹邊形區域轉彎次數最少，因此對于凹邊形區域而言，收割機保持與水平夾角為90°的行走方向為最優作業方案。

凹邊形區域不同角度的指標結果如表2所示：與基于其他方向的作業路徑方案相比，當行走方向θ=90°時，同一收割機比行走方向為100°、135°轉彎次數少10次，優化率達16.7%，比行走方向為0°轉彎次數少20次，優化率達28.6%、比行走方向為45°少6次，優化率達10.7%、比作業沿邊界最長邊方向為29.5°轉彎次數少3次，優化率達5.66%，因此可以得出，基于填補方法的混合優化算法能夠有效處理基于不同角度的凹多邊形農田的收割機調度規劃，并得出全局較優的路徑規劃方案。

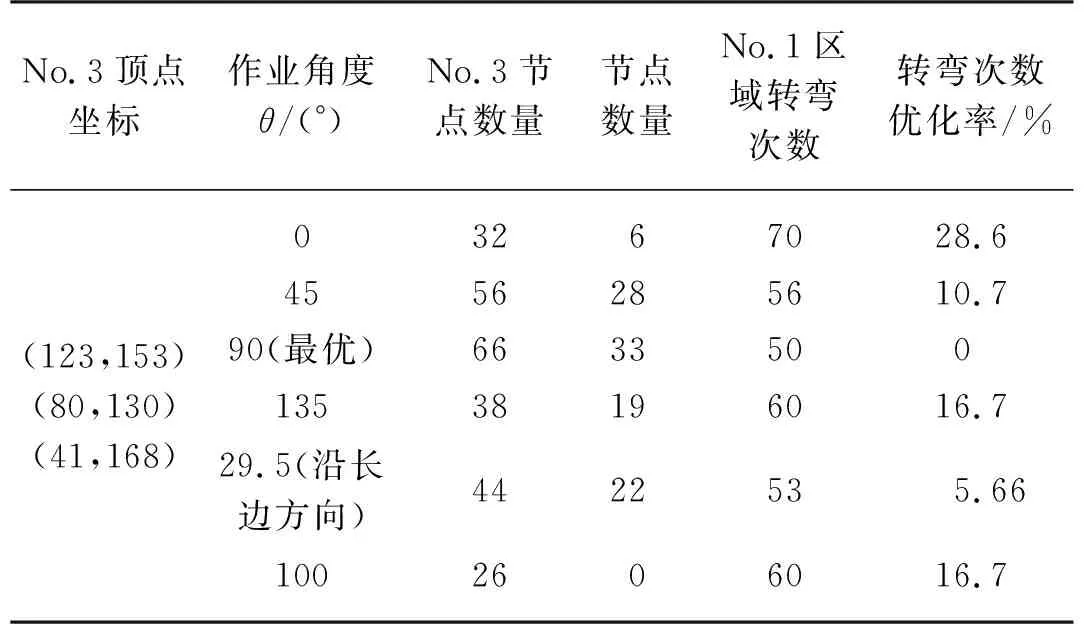
表2 基于不同角度的凹邊形區域指標Tab. 2 Indexes of concave edge area based on different angles

5 結論

1) 單臺聯合收割機田間作業通常采用全覆蓋路徑規劃，主要針對規則區域進行牛耕往復法，對于不規則區域，如凹、凸多邊形農田不同行走方向總會造成收割機轉彎次數增加，影響作業質量、油耗與工作效率。因此本文針對不規則區域的單臺收割機作業角度建立調度模型與設計優化求解算法，實現轉彎次數最少的田間行駛路徑規劃方案。結合仿真算例驗證結果，所提出的優化行走方向算法針對不規則多邊形區域而言能夠有效優化收割機行走方向：在凸邊形農田仿真案例中，該算法求解的最優作業角度是100°，該方向路徑規劃在轉彎次數上要比沿區域最長邊(方向29.5°)牛耕往復的路徑軌跡優化程度為11.32%，比普通方向(行走方向0°、45°、90°、135°等)優化程度達到6%～21.7%；在凹邊形農田仿真案例中，該算法求解的最優作業路徑方向是90°，比沿邊界最長邊(方向29.5°)路徑的優化程度為5.66%，比其他方向(行走方向0°、45°、135°、100°等)的優化程度達到10%～28.6%。

2) 本研究設計了凹凸多邊形轉彎次數求解算法并結合了旋轉搜索算法以獲得復雜邊界區域最優行走方向，形成該區域小麥收割機的工作路徑方案。能夠進一步推廣至實際復雜邊界的農田區域，適用于全覆蓋路徑規劃的轉彎次數優化環節，如小麥收割機收獲作業、小麥、水稻等播種、全覆蓋深耕等具體環節，為減少農機作業轉彎次數，提高作業效率等提供了有效的決策依據。

3) 針對全覆蓋路徑行走方向優化問題，本研究基于單個收割機對單獨農田區域的作業路徑規劃，并未考慮多收割機協同作業方式，未來可以通過大型農田區域劃分的方法解決多機協同問題；同時本研究基于復雜凹邊形進行假想區域填補形成簡單凸邊形，最終獲得轉彎次數，若作業區域含有多個凹形區域，可以利用分割而非填補的思想對不規則凹邊形進行區域劃分，從而將整個不規則區域轉化為若干凸邊形作業區域，每個區域可以產生不同行走方向的優化路線，從而達到整體最優效果。因此未來研究方向可以集中在對復雜邊界環境的區域劃分方式及優化求解等。