LOS＿NLOS下基于PF和最大似然的TDOA定位算法

黃 波，李 偉

(南京郵電大學通信與信息工程學院，江蘇 南京 210003)

1 引言

目前，無線定位的發展突飛猛進[1]，在室外主要是用GPS衛星定位和慣性傳感器定位，能夠較精確地獲取位置信息，但是在室內情況下，由于室內環境的復雜度較高，例如物體的遮擋等原因，GPS很難獲得比較精確的估計[2]。UWB(Ultra-wideband)室內定位由于功耗低、系統結構的實現比較簡單、安全性高、定位精確、工程簡單造價便宜等等優點，在室內定位中廣泛應用于目標定位方向[3]～[6]。

在基于距離的定位策略中，測量節點的距離常采用的方法有基于到達時間(Time Of Arrival，TOA)、到達時間差(Time Of Difference Of Arrival，TDOA)、到達角度(Angle Of Arrival，AOA)及接收信號強度(Received Signal Strength，RSS)等[7][8]，這些方法根據不同的定位策略來確定移動臺的位置。其中， TOA需要節點保持精確的同步，因此硬件設備比較費電，而且對硬件的要求也比較高。AOA在定位過程中需要用到特殊的天線陣列，并且很難獲取準確的測量角度，對信號遮擋也比較敏感。RSS方法雖然算法簡單，但是也容易受到物體遮擋的影響，即在非視距情況下表現不理想[9]～[11]。

TDOA相對誤差更小，而且實現較為簡單，因此應用很廣泛。TDOA技術的核心思想是測量目標節點到達錨點之間的時間差，然后根據到達的時間差值計算距離，最后根據雙曲線定位原理計算出目標節點的位置[12]。

對于TOA和TDOA，定位方程都是非線性的，標準的解決方案是將該非線性的方程先進行線性化，再進行梯度搜索[13][14]。但是這些方案在僅在高信噪比的情況下能夠進行最優的估計，在低信噪比的時候估計的誤差會偏大。文章[15]采用了極大似然(ML)方程的思想，首先采用線性化的思想構造兩個線性方程，線性方程依賴于未知的位置信息，然后，利用位置信息和極大似然的思想來求解線性方程，更新未知的系數。AML使用每次最新的未知信息來檢查ML函數，并選擇最小值作為最優的解決方案。上述算法雖然能較好的估計視距(Line-Of Sight，LOS)傳播的情況，但是在非視距(Non-Line-Of Sight，NLOS)傳播情況下，即由于移動臺在移動的過程中，無線電信號由于物體的遮擋，只能通過反射，散射和衍射方式到達接收端，到達時間就會產生很大偏差，因此上述算法就不能正確的反映接收端和發送端之間的距離或者距離差。

由于粒子濾波(Particle Filter，PF)不受線性高斯條件的約束，并且計算機高速發展，運算速度大大提高，以及粒子濾波良好的跟蹤性能，在目標跟蹤、圖像處理等方面應用廣泛[16]～[18]。為了解決上述問題，抑制和減少NLOS情況下產生的誤差，本文采用了將TDOA算法和粒子濾波算法結合的思想。首先利用TDOA算法通過最大似然的方法得出的結果作為測量值，然后在貝葉斯框架下建立粒子濾波算法對測量結果進行預測，將該算法在NLOS情況下的誤差糾正、抑制，從而提高在目標區域的定位精度。仿真結果表明，在NLOS情況下，粒子濾波算法能夠使定位的結果明顯改善，并且優于無跡卡爾曼濾波(Unscented Kalman Filter，UKF)方法。

2 基于最大似然的TDOA算法

文章[15]基于最大似然的TDOA算法給出了詳細的推導。TDOA是基于距離差異的定位方法，因此產生了時間差，假設定義TDOA時間差的向量為

Td=[t21….tN1]T=T0+e

(1)

其中T0是時間的真實值，e是測量誤差(獨立，零均值，高斯隨機變量)，那么有協方差矩陣

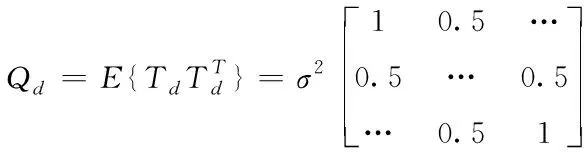
(2)

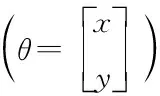
di1=ri-r1

d=[d21…dN1]T

(3)

建立概率密度函數

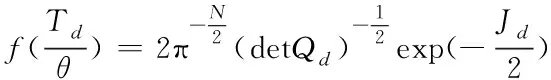
(4)

其中

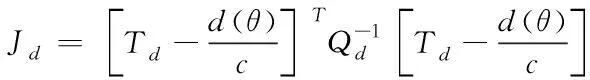
(5)

讓Jd對θ的梯度為0，求導化簡得到一個二次方程組，用RSR算法得到最優根，再由θ計算出Φ，其中

Φ=ΜΛ

(6)

并且

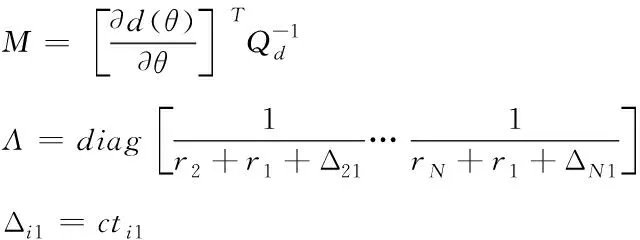
(7)

再次進行上述過程，不斷更新的θ選擇使Jd最小的θ。

3 基于粒子濾波的TDOA算法

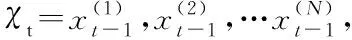
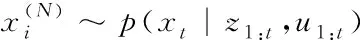
(8)

由(8)式，粒子濾波的核心思想就是用粒子的均值來代替積分運算，從而獲得最小的方差估計。

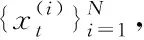
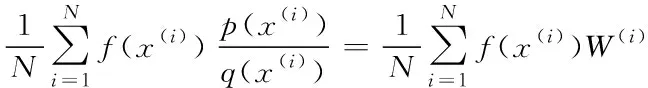
(9)

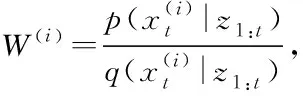
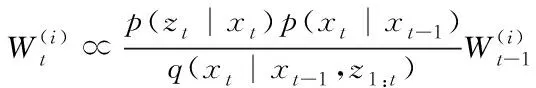
(10)

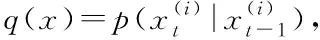
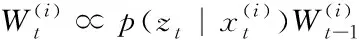
(11)

再利用最大似然的TDOA算法，計算出最優估計，在噪聲很大的情況下，能夠明顯減少TDOA算法的誤差。并且本文提出的方法，將定位估計和消除NLOS誤差分離，即每根據最大似然TDOA算法獲得一個定位結果，便結合上一時刻的粒子狀態，對定位結果進行估計糾正。

基于粒子濾波和最大似然的TDOA定位算法步驟如下：

測量值的獲取：利用基于最大似然的TDOA定位算法獲取當前狀態xt的測量值zt。

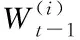
3) 根據最大似然TDOA算法獲取到當前的觀測值zt。

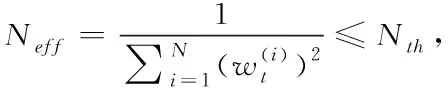
6) 得到估計值：xt。

7) 令t=t+1再次重復上述步驟2)～7)。

4 仿真分析

4.1 單目標多觀測點基于距離的跟蹤模型

假設kT0處的目標的速度為v(k)，加速度為a(k)=u(k)+w(k)，其中u(k)為機動加速度，而w(k)為隨機加速度，由外界因素影響。由運動學公式得

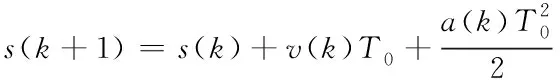
(12)

v(k+1)=v(k)+a(k)T0

(13)

將(12)(13)式寫成矩陣形式如下

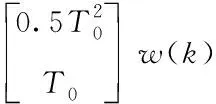
(14)

擴展成四維，即所用的狀態方程為

X(k+1)=ΦX(k)+Bu(k)+Γw(k)

(15)

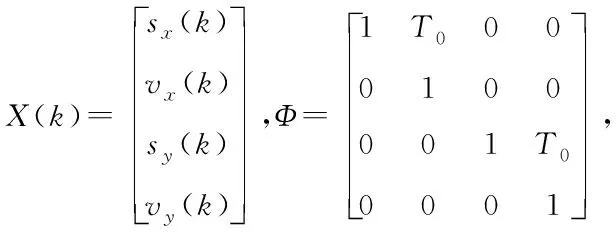
式(12)的狀態方程僅顯示目標狀態的運動狀態，而觀測站不知道目標的具體位置，由于第i個觀測站(xi，yi)與目標之間的距離存在關系

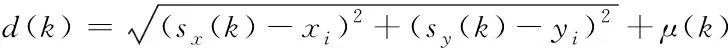
(16)

因此，可以將觀測方程寫作

Z(k)=h(X(k))+μ(k)

(17)

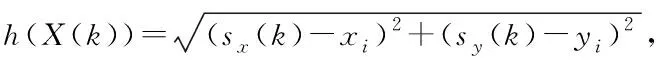
4.2 仿真結果與分析

最大似然TDOA算法在非視距(NLOS)環境下，測量會有很大偏差，為了驗證粒子濾波算法對這種偏差的抑制和糾正，在勻速直線運動中對目標狀態進行跟蹤，并采取了UKF和PF進行跟蹤比較。

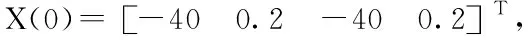
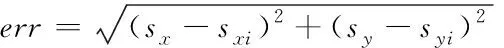
(18)

其中，(sx，sy)是未知節點的位置，(sxi，syi)為第i次實驗估計出的節點的位置的均值。

LOS情況下，取TDOA算法的方差為10cm。圖1截取了部分跟蹤曲線，給出了在LOS情況下，最大似然TDOA算法、粒子濾波算法、無跡卡爾曼濾波算法與目標真實軌跡的比較。可以看出在LOS情況下，粒子濾波算法能起到較好的糾正效果。

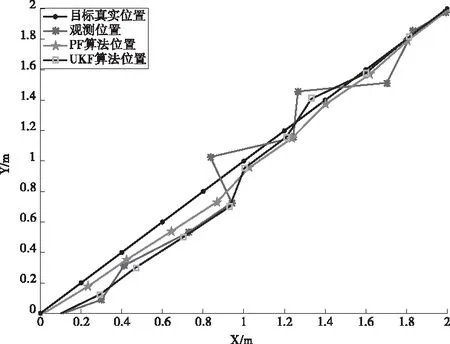
圖1 LOS情況下移動點定位軌跡圖

圖2截取了t=200～300s時刻的誤差圖，給出了各個算法在LOS情況下每個采樣點的誤差情況。由圖二可知，在LOS情況下，大部分采樣點上，PF算法優于UKF算法，并且優于未經過濾波處理時TDOA算法，且由計算得知，PF和UKF算法分別對最大似然TDOA算法的優化效果為：44.31%，33.51%。因此，PF算法在LOS環境中對TDOA算法誤差具有良好的抑制作用。

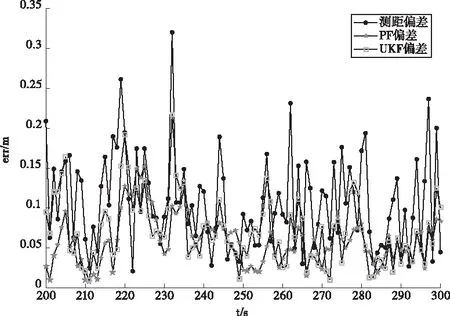
圖2 LOS情況下定位誤差比較圖

為了模擬NLOS環境的情況，本文采用的方法是在某個采樣區間內，加大最大似然TDOA算法的測量誤差，在NLOS情況下，由于信號的散射、反射及物體遮擋等原因，信號到達的方差遠高于LOS情況，因此仿真取TDOA算法的方差為3m，且在t=50～100s模擬了NLOS情況。圖3截取了在模擬NLOS的情況下，部分最大似然TDOA算法、粒子濾波算法、無跡卡爾曼濾波算法與目標真實軌跡的比較圖，可以看到在噪聲較大時，僅由TDOA算法計算得到的觀測位置與目標真實位置偏差很大，UKF+TDOA算法也有較大影響，PF+TDOA算法能夠較好的糾正誤差，能得到較好的定位效果。圖4給出了t=40～130s內三種算法誤差的比較，且由計算得知，PF和UKF算法分別對最大似然TDOA算法的優化效果為：75.95%，40.30%。因此，PF算法在NLOS環境中對TDOA算法誤差具有良好的抑制作用。

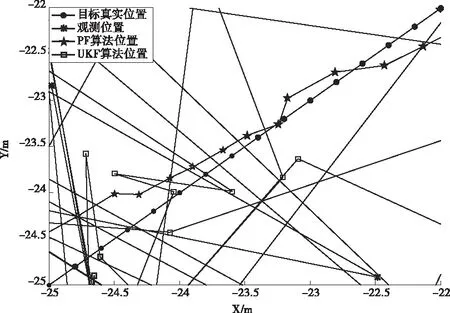
圖3 NLOS情況下移動點定位軌跡圖

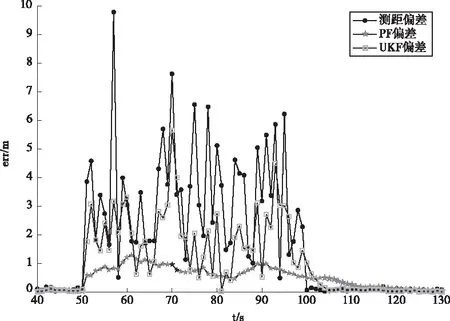
圖4 NLOS情況下定位誤差比較圖

5 結論

本文利用了粒子濾波，實現了對最大似然TDOA算法在室內復雜環境下，對測量誤差較大的測量值進行糾正，解決了TDOA算法中在NLOS情況下的誤差大的問題，并通過仿真，比較PF算法和UKF算法，證明了PF算法具有較高的定位精度，在抑制誤差方面能表現出良好的性能。