優先級評估下的軟件源文件可疑度度量方法
朱镕申,孫川钘,黎 秀
(電子科技大學成都學院,四川 成都 611731)
1 引言
軟件產業的不斷進步,讓計算機領域對軟件質量的需求日漸提升,但也不斷出現軟件源文件代碼缺陷問題,大幅度提升系統事故概率。軟件源文件缺陷表示源代碼內包含語法、拼寫或標點錯誤[1],這樣會嚴重影響用戶的實際操作應用。想要提升軟件質量,一定要有效管理與修復源文件代碼缺陷,對其采取可疑度度量,從而明確產品是否存在缺陷,保證軟件產品的正常使用[2,3]。
關于軟件缺陷檢測問題,文獻[4]利用耦合重啟隨機游走與標簽傳播方法,從軟件調用關聯、模塊風險度與歷史缺陷報告來探究缺陷方位,把缺陷定位劃分成風險度與標簽兩種傳播模式,明確軟件缺陷情況。文獻[5]通過獲取程序函數調用序列,比較待測目標序列與可疑序列,去除已檢測函數,獲得缺陷函數候選集,實現缺陷函數定位。
但上述兩個方法均沒有計算缺陷之間的屬性值,無法完全保障缺陷位置定位準確性。因此本文提出一種優先級評估下的軟件源文件可疑度度量方法。運用優先級評估策略完成源文件可疑度度量大小排序,推算缺陷數據與源文件之間的關聯性,使用基于支持向量回歸的軟件源文件易錯性方法,獲得軟件源文件相對的缺陷密度,從而獲得軟件源文件可疑度,明確源文件產生缺陷的概率。
2 基于優先級評估的軟件源文件可疑度度量方法
在優先級評估基礎上融合軟件源文件缺陷定位有關內容與缺陷預測手段,設計一種基于優先級評估的軟件源文件可疑度度量方法。可疑度越大,證明源文件產生缺陷的幾率越高。創建源文件可疑度度量方法整體架構,具體參見圖1。

圖1 軟件源文件可疑度度量過程
將可疑度計算解析式描述為
Score=(1-a)Score1+aScore2
(1)
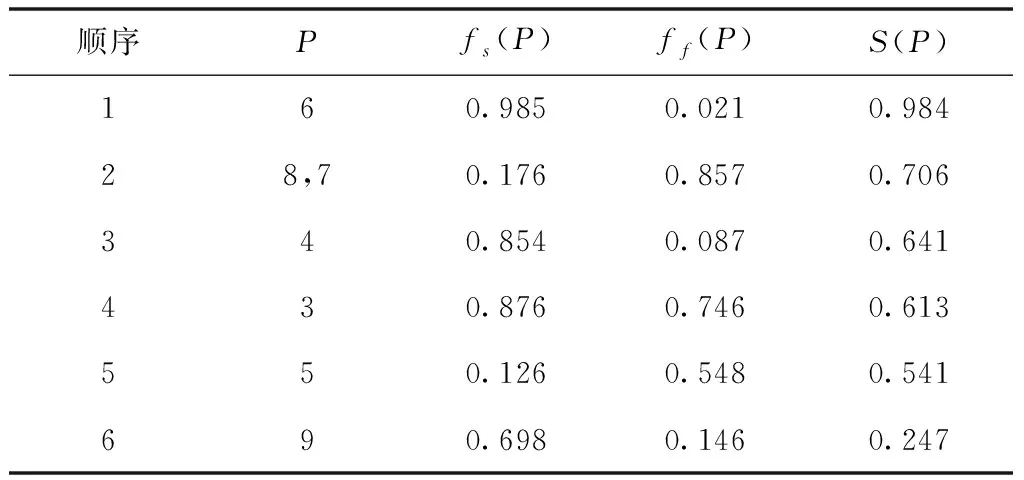
式中,Score1代表源文件和待檢測缺陷的關聯度,Score2是源文件易錯水平,參變量a用于調節關聯度與易錯水平處于可疑度度量過程中的權重,保證0 在計算可疑度之前,首先對其進行定量分析,在可疑度優先級排列的多屬性決策中,決策群體為E={e1,e2,…,en},使用ω描述專家權重。優先級評估排序需求集合是R={r1,r2,…,rk},可疑度需求評估屬性是F,評估屬性權重是λ。 度量決策者es對度量需求ri屬性的打分過程為 (2) (3) 決策群體對度量需求評估的結果通過個體決策與專家權重計算得到,記作 (4) 軟件源文件缺陷通過諸多特征屬性表示,劃分成標稱與序數兩個類別,如表1內的缺陷數據,表內缺陷類別1與2為標稱屬性,3為序數屬性。 表1 軟件源文件缺陷數據表 按照數據挖掘有關定理,數據間的相鄰性包含相似與相異兩種性質。在目標i、j的標稱屬性匹配情況下,相似性sim(i,j)=1,相異性d(i,j)=0。 標稱屬性一般使用布爾度量方法,如果兩個目標互相匹配,相似性等于1,反之等于0。序數屬性與標稱數據的區別在于:具備抽象意義的序數屬性值可使用距離來推算源文件缺陷相似度[8],計算過程為:首先設置第i個目標的序數屬性f的值是rif,屬性f內含有Mf個有序狀態。其次,因為每個序數屬性極有可能產生差別較多的狀態數,為了讓屬性間的相異性處于(0,1)取值范圍內,要規范化屬性值,得到 (5) 再把缺陷序數屬性實施距離計算,針對單屬性來說,使用歐幾里得距離[9]描述兩個缺陷樣本間的相異性大小 (6) 融合粗糙集理論與模糊聚類算法解析軟件缺陷數據,劃分缺陷屬性權值,詳細過程如下: 第一,構建缺陷數據編碼表,抽象化處理數據,每個缺陷均是通過n個抽象化特征值定義的矢量,將全部缺陷數據當作特征空間內的多維矩陣,表示成 (7) 第二,組建模糊相似矩陣T,推導過程為 (8) 式中,n表示矩陣列數。 第三,分割不同的臨界值面積來闡明缺陷數據間的相似性,按照模糊等價矩陣內的缺陷數據相似性,分別把缺陷數據劃分成各不相等的類型。 第四,利用粗糙集內關鍵性定理算出屬性權重值。將缺陷數據劃分結果D的特征屬性C依賴度描述成 γ(C,D)=|POS(C,D)|/|U| (9) 其中,|POS(C,D)|代表正域的缺陷數量,|U|代表缺陷數據非空集合內的缺陷數目。 將屬性的關鍵性記作 SGF(f,C,D)=γ(C,D)-γ(C-{f},D) (10) 則屬性全局關鍵性為 (11) 根據屬性的關鍵性排名,推算每個屬性自身的權重值 (12) 由此將缺陷數據與軟件源文件的相關性推導公式記作 (13) 式中,Similarity(B,Si)是缺陷數據與過往修正缺陷的相似性,m是全部和源文件相關的缺陷個數。 為了保證軟件源文件可疑度度量的正確性,首先要明確軟件缺陷的度量元。以往缺陷定義均采用代碼行當作度量準則[10],而后又相繼研發出一系列面向目標的軟件研發技術,得到軟件度量元,例如內聚性、耦合性等。本文方法的度量元如表2所示。 表2 軟件源文件缺陷定位度量元 易錯性即為源文件缺陷密度大小,密度越大,易錯性越強,可疑度越高。代入Spearman秩相關數算法,衡量度量元和源文件缺陷密度間的關聯,得到對缺陷密度影響最高的度量元,并剔除多余度量元。假設軟件源文件的度量元為H,缺陷密度為I,把H、I內的數據實施匹配,獲得數據集合(H1,i1),…,(Hk,ik),把Hk、ik依次根據大小排列,得到二者在第二個次序樣本內的排名,定義成Rk、Sk。則H、I之間的關聯水準計算公式為 (14) 為防止數據處理時由于某些度量元數值差異較多影響運算正確率,需要預處理數據。歸一化是把度量元屬性值整合至[0,1]區間。歸一化單個維度下的度量元數據,得到 (15) 使用支持向量回歸完成源文件代碼易錯性預測。設定一個數據集{(h1,i1),…,(hl,il)},hl是第l個軟件源文件的度量元矢量,il是第l個源文件缺陷密度。使用Rn內的函數f(x)進行數據擬合,函數的表達式為 f(x)=w·x+b (16) 其中,w代表超平面的法矢量,b是一個任意常數。 可疑度度量的計算過程就是探尋一個最佳超平面,讓全部樣本點與超平面的偏差總值距離為最短,使用具備正則化特征的偏差函數進行距離運算,得到 (17) 其中,f(xe)是第e個軟件項目缺陷密度評估值。 將軟件源文件易錯性問題變換成最優問題,得到 (18) (19) 代入一個拉格朗日乘子α,獲得如下對偶表達式: (20) 其中,K(xi,xj)是一個核函數。 最終得到支持向量回歸下的易錯性預測模型是 (21) 利用式(21)即可在輸入任意度量元矢量的情況下,得到軟件源文件相對的缺陷密度,完成易錯性計算全過程。 挑選模型內的核函數,恰當的核函數可把低維空間非線性問題變換成高維空間線性問題,探尋回歸問題的最佳超平面。運用徑向基核函數優化預測模型,將優化過程描述成 (22) 其中,xj表示徑向基核函數中心位置,σ是徑向基核函數的寬度指數,與核函數徑向作用區域面積有直接關系。 模型參變量優化的根本含義是面向各類性質不同的目標擇取恰當的(C,g)數據對。在缺陷密度預測模型內設定C、g的取值范圍,按照搜尋步長把C、g依次分割成n1、n2個集合,再匹配合適的數值,組成n1·n2個(C,g)數據對。利用網格搜尋實現參變量遍歷搜尋,并將預測準確率最大的(C,g)數據當作最優參數,實現易錯性預測評估,并綜合缺陷數據與源文件的關聯性計算結果,二者相加實現高精度軟件源文件可疑度度量。 利用仿真證明所提方法的性能優越,所使用的仿真環境為2GHzCPU、內存2G的計算機,實驗平臺為Matlab 7.1。創建兩個不同的待測程序,各個程序內均涵蓋一個缺陷。將軟件源文件中的代碼作為實驗對象,計算其可疑度大小,利用本文算法思想,以源文件謂詞代碼為例,將其可疑度計算過程描述為 Φ(P)=nt(P)/(nt(P)+nf(P)) S(P)=-lg(sim(fs(P),ff(P))) (23) 式中,nt(P)是謂詞代碼,P是無缺陷的次數,nf(P)是有缺陷次數,S(P)是可疑度,sim(fs(P),ff(P))是隨機相似度函數。 將本文方法下的兩個待測程序謂詞代碼可疑度度量結果表示成表3與表4。 表3 待測程序1的可疑度列表 表4 待測程序2的可疑度列表 在表3與表4中,可疑度S(P)是fs(P)和ff(P)二者間的差異,S(P)值越趨近1,證明軟件源文件謂詞代碼P具備缺陷的概率越高,即可疑度越大,反之概率越低,可疑度越小。 通過實驗結果看出,包含缺陷的第6個與第15個謂詞代碼可疑度為最高,排在可疑度表格的首位,且可疑度從大到小排序,逐步趨近于0。在兩個表格內,第8個與第7個的謂詞代碼可疑度相同,表明兩個分支在源文件內具備同時執行與不執行的耦合關聯,則依照實驗結果,缺陷檢測人員首先要勘測可能包含缺陷的分支語句,缺陷極有可能隱藏在分支語句中,實現了預期可疑度度量目標。 為進一步驗證本文方法的可靠性,將軟件數據集SWT3.1作為實驗對象,和文獻[4]、文獻[5]進行可疑度度量分析,表明本文方法對提升軟件源文件缺陷定位的實用性。實驗中使用三類指標用于衡量可疑度度量缺陷定位方法的性能,TopN表示返回結果內缺陷文件的定位個數,平均倒數排名是對全部的排序進行統計分析的過程,排名值越大,表明方法計算正確率越好。平均精度是對全部排序表的全局評估。將三種方法的缺陷定位結果表示成表5。 表5 SWT3.1數據集缺陷定位結果對比 從表5可知,本文方法三種指標的值均為最高的,證明該方法較比文獻方法,在源文件可疑度度量方面占據更大的優勢。這是因為本文方法采用優先級評估算法,運用評估結果明確軟件源文件可疑度大小,讓軟件研發者有更充裕的時間完成缺陷修復,讓軟件安全平穩運行。 面向軟件源文件代碼缺陷問題,提出一種優先級評估下的軟件源文件可疑度度量方法。所提方法使用優先級評估手段排列軟件源文件缺陷可疑度大小,并快速計算出缺陷數據與源文件的關聯性,運用支持向量回歸方法創建易錯性預測模型,完成高質量軟件源文件缺陷定位目標。在下一步工作中,會簡化權重計算方法,增強方法計算效率。2.1 基于優先級評估的問題描述





2.2 缺陷數據與源文件的關聯性計算








2.3 支持向量回歸下的源文件易錯性計算

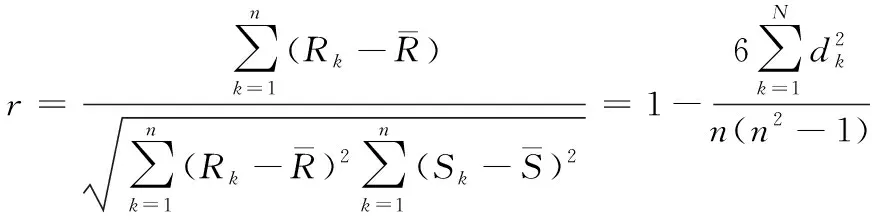


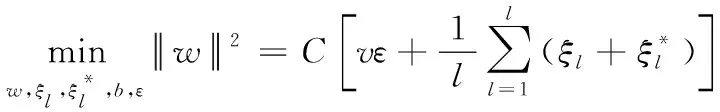

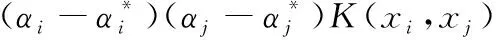

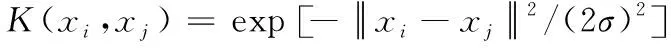
3 仿真研究


4 結論

