“三定法”教你輕松搞定函數圖象共存問題

白銀市第十中學 高麗娟

1 引言

圖象與性質是函數中難以剝離的兩個內容，要想提高函數整個知識點的理解與運用程度，就離不開分析它的圖象和性質[1].所以，本文中推出“三定法”，嘗試探究與分析函數圖象的共存問題，以幫助學生掃除“障礙”.

2 理論基礎

函數圖象共存常涉及正比例函數、一次函數、反比例函數、二次函數的圖象，是同一直角坐標系中一種或多種圖象的綜合.所以，要想解決圖象共存問題，先要弄清楚這幾種函數的圖象及性質，詳見表1.

表1

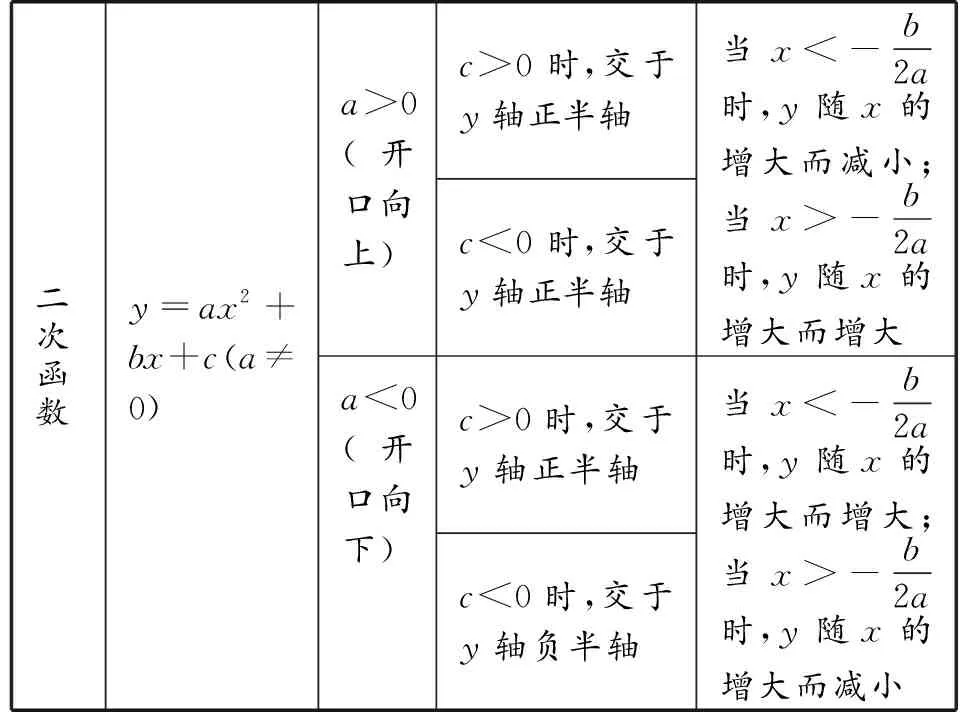
(續表)

3 “三定法”說明及例析

本文中所指的“三定法”，是解決函數圖象共存問題的一種方法，主要有如下三個步驟：

第一，定圖象.由于函數圖象共存問題中常出現兩個圖象，所以以哪個圖象為基礎分析問題非常關鍵.選擇哪個圖象并沒有定法，可據題意靈活選擇.

第二，定符號.在選擇基礎圖象后，就要根據該圖象分析出相應系數的符號.如分析正比例函數中k的正負、一次函數中k和b的正負、二次函數中a和b，c的正負等.

第三，定結論.在定好基礎圖象對應的系數符號后，就需要將之與另一圖象對比.若系數的符號在兩個圖象中一致，則圖象可共存；反之，則圖象不可共存.

本方法的三個步驟具有一定的順序，在分析問題時，只要任何一個順序錯誤，利用本種方法分析問題將無法達到預期效果.

下面，結合例題分別從正比例函數和一次函數圖象、一次函數和反比例函數圖象、一次函數和二次函數圖象等幾種共存情形出發，具體分析如何解決圖象共存問題.

3.1 正比例函數和一次函數圖象共存

例1如圖1,函數y=kx-k2和y=-kx(k為常數，且k≠0)在同一坐標系中的圖象可能是( ).

圖1

解析：選項A中的正比例函數過二、四象限，所以-k<0，那么k>0.再看一次函數圖象，它過一、二、三象限，所以k>0，這一點與正比例函數中的k保持一致.如果k>0，那么-k2應該小于0，所以一次函數的圖象應該與y軸的負半軸相交.但是選項A中一次函數圖象與y軸交于正半軸.這一點矛盾，所以選項A錯誤.

選項B中的正比例函數也是過二、四象限，所以-k<0，那么k>0.再看此時的一次函數圖象，它過一、三、四象限，所以k>0，這一點與正比例函數中的k保持一致.如果k>0，那么-k2<0，所以一次函數的圖象應該與y軸的負半軸相交.選項B中一次函數圖象與y軸正好交于負半軸，所以選項B正確.

選項C中的正比例函數是過一、三象限，所以-k>0，那么k<0.在同一平面直角坐標系中的一次函數的圖象過一、二、四象限，所以k<0，這一點與正比例函數中的k保持一致.如果k<0，那么-k2<0，所以一次函數的圖象應該與y軸的負半軸相交.然而，選項C中的一次函數圖象卻與y軸正半軸相交，由此判斷C錯誤.

選項D中的正比例函數是過二、四象限，所以-k<0，那么k>0.在同一平面直角坐標系中的一次函數的圖象過二、三、四象限，所以k<0，這一點與正比例函數中的k相反，矛盾.所以選項D錯誤.

故本題應選：B.

評析：在分析本題中的每個選項時，“三定法”得到了完美展現.首先，確定正比例函數圖象為基礎圖象，然后分析k的正負符號，再與另一直線對比尋找符號是否一致.從中也可以發現，用“三定法”分析圖象共存問題時，需對每個選項逐個分析，直至找到符合題意的選項.

3.2 一次函數和反比例函數圖象共存

圖2

圖3

評析：這是近幾年中考考查圖象共存問題比較新穎的方式，與例1常規考法有較大差別，但“三定法”同樣適用，只是需作靈活處理.所以，在基礎題上作適當延伸和拓展，對學生掌握“三定法”有利.

4 “三定法”的注意事項

首先，函數圖象共存問題中，通常會畫出若干種函數的圖象.學生在分析這類問題時，始終要注意分辨，不能混淆圖象，更不能將系數的正負符號分析錯誤.

其次，函數圖象共存問題有多種不同的類型，無論是哪一類圖象共存問題，它們的解題方法都可利用本文提到的“三定法”.對與例2類似的圖象共存問題，則需根據所給出的圖分析出系數正負符號，然后再與所給選項對比，該類問題考查形式相對更加靈活，需引起注意.

最后，對于多種函數解析式中相同的字母，它們的正負符號也一定相同.如例1中的“一次函數y=kx-k2和正比例函數y=-kx(k為常數，且k≠0)”，這里的k不僅是比例系數，而且-k2構成了上述所講的b.分析時，一定要將此分離開，切忌混淆.

5 結語

總之，“三定法”作為本文提出的一種解決函數圖象共存問題的方法， 在整個使用過程中，要準確把握與函數圖象及性質有關的理論基礎，這是三定法”解決問題的依據，只有這樣才能分析兩個函數圖象是否存在矛盾之處，找到正確答案[2].