探析初中數(shù)學(xué)中轉(zhuǎn)化與化歸思想的實(shí)踐應(yīng)用

江蘇省無錫市大橋?qū)嶒?yàn)學(xué)校 陳建忠

初中數(shù)學(xué)呈現(xiàn)出的主要特征是抽象.很多數(shù)學(xué)問題需要通過聯(lián)想、分析、類比等思維進(jìn)行轉(zhuǎn)換，才能夠?qū)⒃静⒉皇煜さ膯栴}轉(zhuǎn)化為已經(jīng)掌握的問題，進(jìn)而完成問題求解.而數(shù)學(xué)問題轉(zhuǎn)化的過程被稱為轉(zhuǎn)化與化歸.從本質(zhì)上來講，轉(zhuǎn)化與化歸思想充分揭示了聯(lián)系數(shù)學(xué)問題實(shí)際，完成知識點(diǎn)轉(zhuǎn)化的過程，除卻原本就非常簡單的數(shù)學(xué)知識，其他的數(shù)學(xué)問題都需要經(jīng)過轉(zhuǎn)化方式來實(shí)現(xiàn)求解.可見，轉(zhuǎn)化與化歸思想是求解數(shù)學(xué)問題的基本思想.本文中將就初中數(shù)學(xué)中的轉(zhuǎn)化與化歸思想的實(shí)踐應(yīng)用展開詳細(xì)探討.

1 復(fù)雜問題簡單化

初中數(shù)學(xué)知識教學(xué)中，教師通常會引導(dǎo)學(xué)生將原本比較復(fù)雜的問題以化歸方式逐漸轉(zhuǎn)化為簡單問題，而學(xué)生先解決自己熟悉的簡單問題，最終逐步達(dá)到解決復(fù)雜問題的目的.該種解決問題的方式被稱為簡單化，是獲取復(fù)雜問題解題思路的主要依據(jù).

例1如圖1，樓梯的高度為2 m，∠BAC=30°，此時在樓梯表面鋪設(shè)地毯，求地毯的長度.

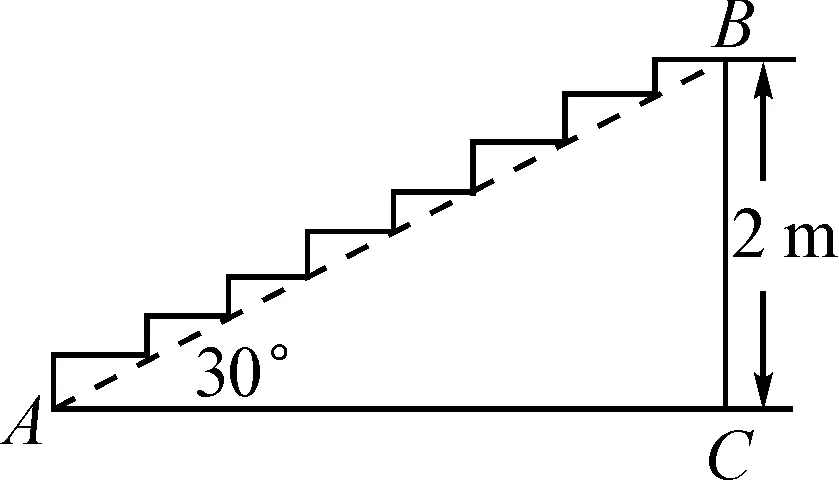
圖1

解析：連接AB.

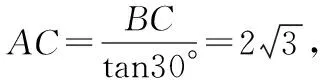
上述解題步驟中，率先考慮的思路是分別求出每個臺階上的地毯長度，然后將這些長度相加.但是，因?yàn)椴恢烂總€臺階的具體高度和寬度，因此，如果直接采用這種長度相加的方式求解，思路會受到限制.如果在圖形中能夠觀察到將A，B兩點(diǎn)連接以后形成了多個小直角三角形，其中較小的銳角均為30°，而且題目中給出已知條件樓梯的高……