“雙減”背景下初中數學作業設計的策略研究
——以二次函數為例
西華師范大學 張瑋芳
1 引言
“雙減”政策要求中學生的課下作業時間總量不超過一個半小時,而對于數學作業,時間應在 20 分鐘左右,這就要求教師所布置的課后作業要“少量高效”[1].但現階段很多老師依舊按照傳統的方式布置作業,盲目地留大量的習題,推行“題海戰術”,結果卻不盡如人意,學生不僅沒有熟練地掌握所學知識,還增加許多負擔.那么如何提高數學作業設計質量,使學生“減負高效”地掌握所學知識,是筆者主要思考的問題.現就該問題提出一些策略.
2 充分了解學生,加強作業題目間的聯系
想讓學生通過作業高效鞏固課堂所學的新知識,教師必須充分了解學生,針對學生普遍不熟練的知識布置作業,做到“對癥下藥”.教師要在課前、課中、課后積極地與學生溝通,得到切實有效的反饋.學生知識的掌握程度如何,哪部分知識薄弱難以理解等,這些都要做到心中有數.布置作業時,題目不能東拼西湊,要注意加強題目間的聯系.比如,對于學生來說,二次函數的最值問題一直較難,這時我們要選取多個從不同角度考查二次函數最值問題的習題.順序要由易到難,由簡到繁,盡量讓每道題都有前幾題的思路或者結論作為基礎,讓學生邊解題邊思考,像上臺階一樣循序漸進地掌握知識.
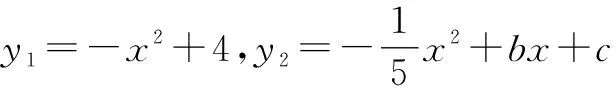
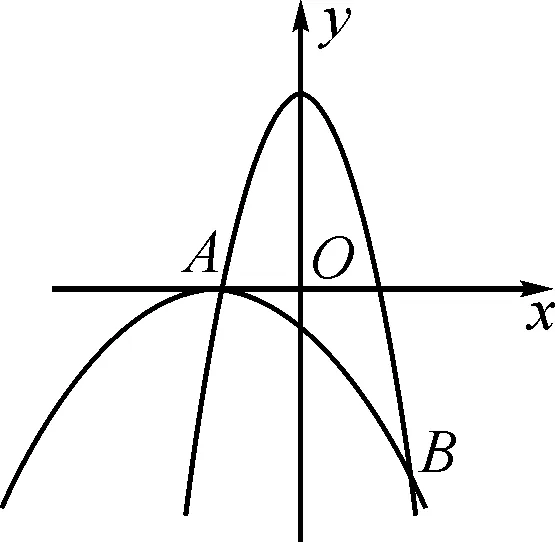
圖1
作業2如圖2,開口向下的拋物線與x軸交于點A(-1,0),B(2,0),與y軸交于點C(0,4),點P是拋物線上的一點,且位于第一象限,求四邊形CABP面積的最大值.
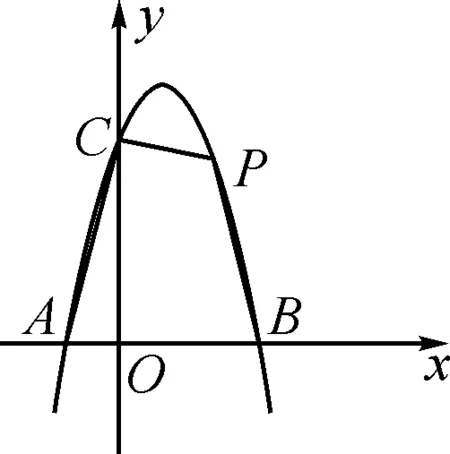
圖2
分析:這兩道題目都屬于二次函數的最值問題,題目之間看似獨立卻又相互聯系.第一題求的是三角形ABC面積的最值問題,通過C,D在拋物線上,設出點C,D的坐標,得到線段CD(長度)的表達式,求出CD的最大值,進而求出三角形ABC的面積.第二題所用思想方法與第一題相同,但本題涉及到四邊形CABP面積如何表達的問題,將四邊形CABP合理分割后,其面積可以表達為三個三角形面積之和,再通過設點的坐標求出四邊形面積的最值.綜上所述,這兩道題的聯系十分緊密,所用到的數學思維方式貫穿始終,由三角形的面積最值擴展到四邊形的面積最值.可見第一題為第二題的解答打下基礎,整個過程循序漸進,對學生的要求也越來越高.經歷這樣的過程,學生將學會在解題中思考,不斷進步,從而達到較高水平.
3 合理分組,加強作業的針對性
每個學生都是獨立的個體,對于每一章的知識都有自己薄弱的環節,要想從根本上提高學習成績,必須將這些薄弱環節都逐個擊破,而合理分組可以針對性地幫助學生解決問題[2].例如,對于二次函數的作業,教師可以依據不同的知識點將練習題進行分組,如:A組重點是二次函數的定義及性質;B組重點是一元二次方程與二次函數的關系;C組重點是生活中的二次函數.同時,學生根據自己的學習狀況自由選擇其中一組或多組作業進行練習,這樣就加強了數學作業的針對性.教師也可以依據難度將題目進行分組,基礎較差的同學選擇難度較小的題目,基礎較好的同學選擇難度較大的題目.總之教師可以依據自己班級的實際情況,對題目或者學生進行合理的分組.這樣在一定程度上保證了學生作業的個性化,增強了作業的針對性,有助于提高學生的學習成績,同時教師的任務也不會過于繁瑣.
作業3A組:已知函數y=(m+3)xm2+4m-3+5是關于x的二次函數.
(1)若該函數的圖象開口向上,求m的值;
(2)若該函數有最大值,求m的值.
B組:如圖3,函數y=ax2+bx+c(a≠0)的對稱軸為直線x=2,若x1,x2是一元二次方程ax2+bx+c=0的兩個根,且x1 圖3 A.x1+x2<0 B.4 C.b2-4ac<0 D.ab>0 C組:A,B兩地生產同一品種的蘋果,共100箱.A地生產蘋果的總成本y(單位:元)與蘋果數量x(單位:箱)之間存在函數關系y=ax2+bx,當x=10時,y=400;當x=20時,y=1 000.B地生產蘋果的每箱成本為70元.從A地把該蘋果運往C,D兩地的費用分別為m元/箱和3元/箱;從B地把該蘋果運往C,D兩地的費用分別為1元/箱和2元/箱.C地需要90箱,D地需要10箱,當A,B兩地生產這批蘋果的總成本的和最少時,寫出A,B兩地總運費的和的最小值. 分析:以上三題是依據知識點將題目進行分組,其中A組題目較為基礎,學生只要充分理解二次函數的定義即可解題.B組題目難度有所增加,需要學生對二元一次方程與二次函數的關系有深刻認識,并能與圖象相結合進行解題.C組題目難度更大一些,與現實生活相聯系,需要學生具有一定的數學閱讀能力,能從語言文字中抽象出數學問題,再通過相關知識進行解題.A,B,C三組題目難度是依次上升的,學生可以依據自己的能力自由選擇,這樣就增強了作業的針對性,有利于鞏固學生相對薄弱的知識點,增強學生自信心. 對于數學的學習,及時總結與復習是相當重要的.經過一階段的學習后,教師應有計劃地設置專題性數學作業.這里的專題作業主要指兩類,一是根據題目涉及的數學思想方法分為不同的專題,二是將每一階段所學的知識進行匯總形成不同的專題[3].對于第一類,教師可以根據每道題涉及的數學思想方法進行分類,例如,數形結合思想專題性作業、化歸思想專題性作業等等.對于第二類,教師可以將該段時間所學的知識進行梳理,總結出重難點、高頻考點等,再通過這些知識點,篩選一些與之匹配的典型的、重點的習題組成一份專題性的數學作業.專題性作業不應該局限于一個單元,只要是有所關聯的知識點,甚至是一些探究活動都可以組成專題,例如函數專題作業、平面幾何專題作業等等.專題性數學作業也不局限于以上兩類,教師可以根據學生的實際情況設置多樣化的數學專題性作業.以二次函數為例,可設置如下數形結合思想專題性作業. 作業4已知拋物線y=ax2+bx+c經過A(2,0),B(3n-4,y1),C(5n+6,y2)三點,對稱軸是x=1,關于x的方程ax2+bx+c=x有兩個相等的實數根. (1)若n<-5,試比較y1與y2的大小; (2)若B,C兩點在直線x=1的兩側,且y1>y2,求n的取值范圍. 作業5平面直角坐標系xOy中,O為坐標原點,點C在y軸正半軸上運動,二次函數y=x2與過點C的直線交于A,B兩點,且CB=3AC,P為CB的中點,設點P的坐標為(x,y)(x>0),寫出y關于x的函數表達式. 分析:作業4和作業5解題過程中都要畫圖,利用數形結合思想解題.作業4中未知數較多,學生在畫圖過程中可能有些吃力,但只要充分理解題意,解題過程并不復雜.作業5作圖相對簡單,但需要學生具有一定的幾何基礎,將代數知識與幾何知識相結合才能解題,在此過程中,學生將體會到代數與幾何的密切聯系,感受到數學嚴謹的美. 教師應該充分認識到作業對于發展學生數學能力的重要作用.運用恰當的策略布置作業,以保證作業的科學性、題型的多樣性.設計出內涵豐富、具有個性的作業.切實地鍛煉學生數學思維,提升數學素養.讓學生在完成作業的過程中感受到數學邏輯的嚴謹性,數學的美,從而發展學生的數學才能.同時,教師布置作業一定要以學生為本,關注學生的成長,關注學生數學思維的培養和數學能力的提升;布置作業要遵循循序漸進的原則,扎扎實實地幫助學生鞏固課堂所學的知識,讓每個學生都能從作業中體會到學習數學的成就感,培養數學學習的信心.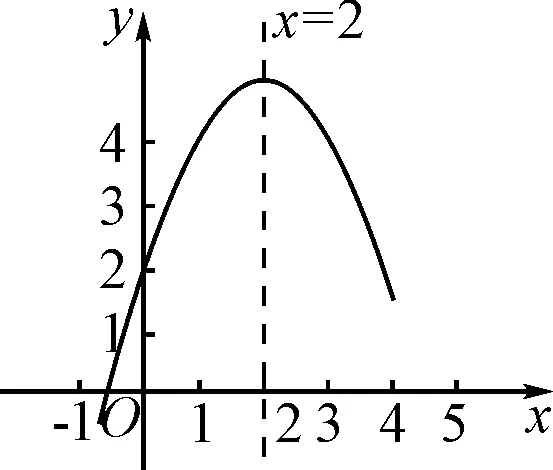
4 及時總結,設置專題性作業
5 結論

