柴油發電機帶雷達脈沖負載仿真研究

趙志魁，徐 曄，黃克峰，徐才華

(陸軍工程大學國防工程學院，南京 210007)

1 引言

隨著信息技術的迅速發展，以相控陣雷達為代表的典型脈沖負載在電力系統中所占比重越來越高。其負荷特性具有峰值功率高，平均功率低的特點，且呈連續的脈沖特性，與傳統的線性負載不同，脈沖負載運行時對電力系統形成反復的加卸載作用，影響電力系統的穩定性。具有大容量、大機組特征的公用電網，因其容量相對于負載可以近似為無窮大，且系統的慣性也非常大，因此負載功率的頻繁突變并不會引起電網電壓和頻率的大幅波動，對電網的影響基本可以忽略。但對于容量和慣性都比較小的柴油發電機組來說，負載功率的頻繁突變會給柴油發電機組帶來“大麻煩”。

柴油發電機組中柴油機作為原動機，通過轉軸帶動同步發電機以同步轉速旋轉，同步發電機的定子線圈切割以同步轉速旋轉的磁力線，對外輸出頻率和幅值穩定的三相交流電，具有體積小，機動方便，供電可靠和易維護的特點，應用十分廣泛。由于脈沖負載功率頻繁的周期性的大幅度發生變化，引起柴油發電機組的輸出電流發生大幅度的變化，激變的定子電流加劇發電機的電樞反應，使得交流電流諧波增加，造成輸出電壓畸變，且負載功率的頻繁突變還會造成柴油發電機組的轉矩不平衡，引起轉速波動。因此對脈沖負載進行建模，研究其工作特性和對柴油發電組的影響具有重要意義。

在針對雷達脈沖負載建模的研究中，文獻[4-6]中基于同步發電機-整流器系統，研究了雷達脈沖負載參數變化時對供電系統動態指標的影響規律。文獻[7]基于雷達發射單元的脈沖負載特性，建立了發射單元的等效電路和數學模型，分析了電壓突變的產生機理。但由于雷達類型和工作模式較多，以上文獻中的雷達脈沖負載都是針對單個重復脈沖而建立的脈沖負載，工作模式比較簡單，不能較為全面的反映雷達脈沖負載的工作特點。因此，本文建立具有代表性的由脈沖串組成的雷達脈沖負載模型，基于柴油發電機組系統，在Simulink中搭建仿真模型，研究雷達脈沖負載的工作特性及對柴油發電組的影響。

2 雷達脈沖負載建模

現代相控陣雷達一般采用的是天線陣列后接TR組件布局，在發射時需要提供很大的功率用于發射功率輸出，而在接收時則僅需要較小的功率維持，因此發射通道負載工作狀態表現為脈沖的特點。考慮到在實際工程實踐中，無法準確獲得雷達內部結構，因此在對其進行建模分析時，把TR組件負載作為“黑箱”處理，只需要模擬其負荷外特性即可達到研究的目的。

2.1 脈沖負載工作特性與結構組成

實際上，雷達的工作脈沖波形大多為非理想矩形波形，如圖1(a)所示，在脈沖持續期間的頂部存在波動和傾斜，脈沖的上升沿和下降沿的時間也有所區別。為簡化分析和研究，并考慮到脈沖負載的可量化以及可實現性，本文對實際脈沖波形進行了簡化處理，如圖1(b)所示。盡管圖1(b)所示的理想矩形脈沖波形不能完全準確地反映出圖1(a)中的部分細節，但是它還是可以反映出雷達工作時主要負荷變化特性。因此，從脈沖負載的基本負荷特性出發，通過建立脈沖負載的仿真模型，對實際雷達工作特性的研究具有理論意義。

圖1 非理想矩形脈沖波形(a)和理想矩形脈沖波形(b)圖

2.2 脈沖重復間隔

脈沖重復間隔PRI(pulse repetition interval)是雷達脈沖信號的重要參數之一，定義為同一個雷達輻射源的相鄰2個脈沖到達時間TOA(time of advent)的間隔。隨著信息技術的發展，不同雷達系統的PRI可能存在多種不同的工作模式，常見的有PRI固定模式、PRI參差模式、PRI滑變模式和PRI抖動模式等。由于本文是針對PRI參差模式進行建模，因此只對PRI參差模式進行介紹。

在PRI參差模式中，雷達脈沖信號以脈沖串形式存在，脈沖串中包含兩個或兩個以上的脈沖重復間隔，將不同的脈沖重復間隔按照一定順序排列，重復利用這些脈沖串信號，信號的重復周期稱為幀周期，幀周期內各個不同的PRI稱為子周期。對于子周期個數為k的PRI參差脈沖信號，幀周期為：

(1)

圖2表示的是PRI參差模式的雷達脈沖信號時域形式，脈沖信號按照幀周期重復出現。

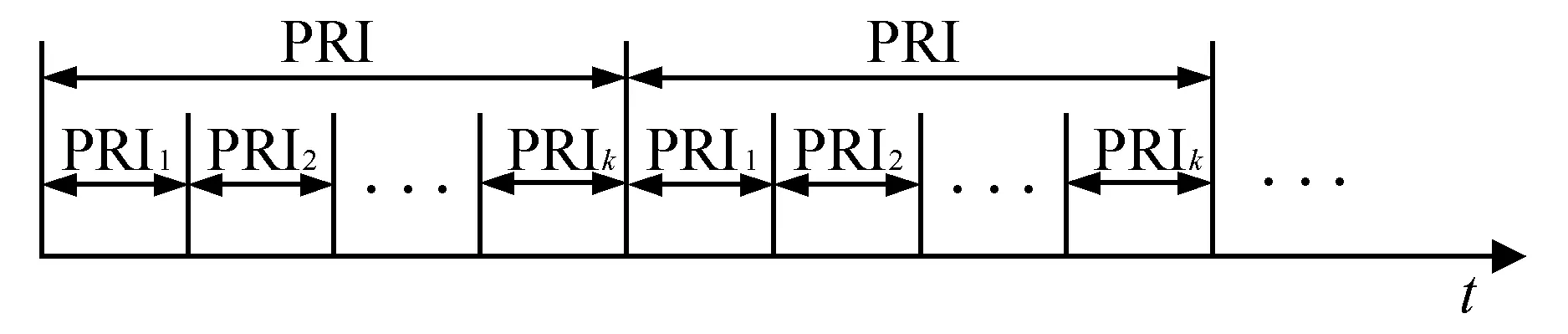
圖2 PRI參差模式雷達脈沖信號示意圖

PRI表示的是雷達信號在時域上脈沖與脈沖之間的間隔，不考慮單個脈沖具體是什么表現形式，但實際上脈沖信號有幅度和寬度上的大小，在進行建模時，必須要考慮脈沖的幅度和寬度，且脈沖的幅度(峰值功率)、寬度(占空比)以及出現的周期(工作周期)決定了脈沖負載的工作特性。圖3表示PRI參差模式的雷達在三相系統中的負載電路。

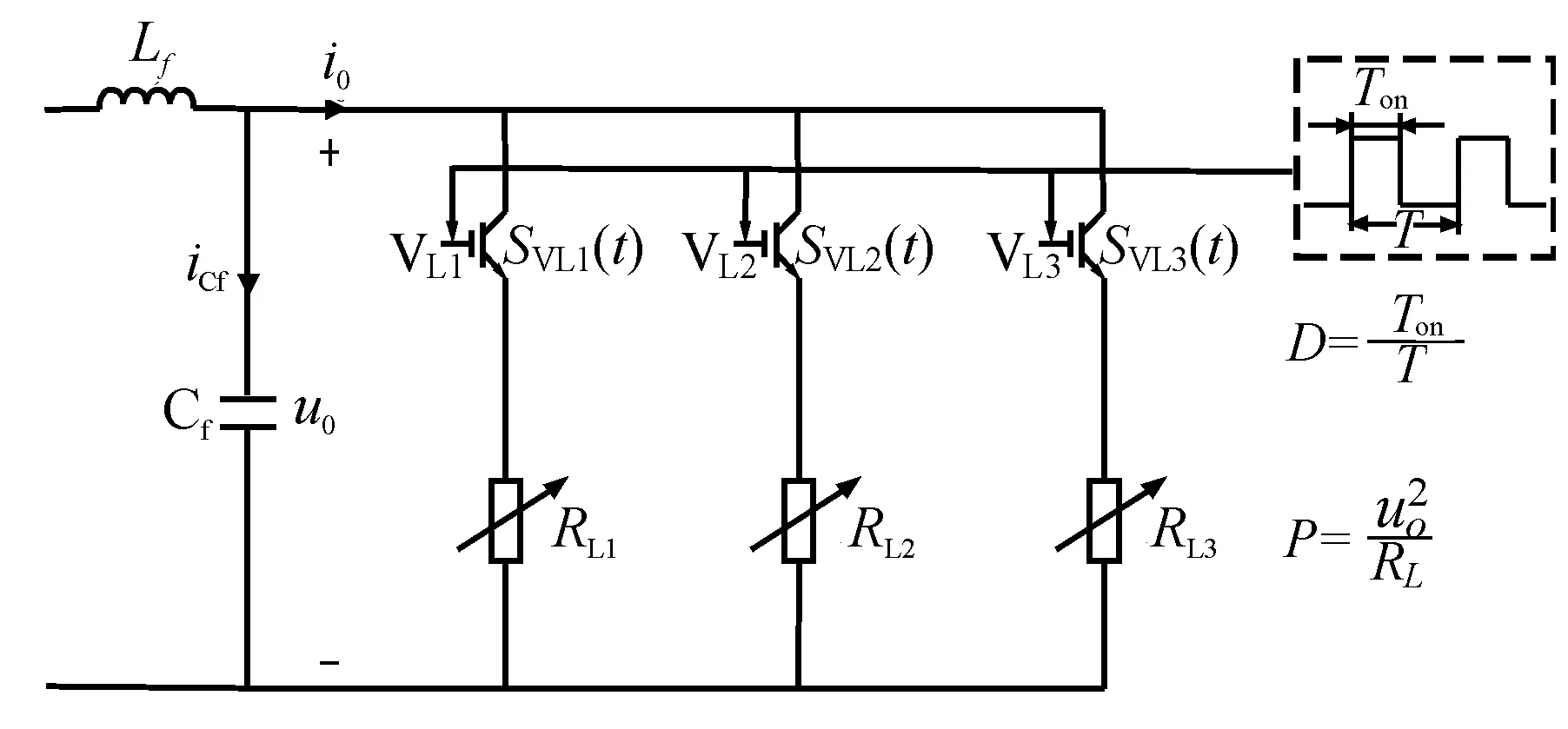
圖3 三相不可控整流器及脈沖負載電路圖

在圖3中，直流開關負載由3組全控開關和可變電阻相互配合組成，它既可模擬脈沖負載各種固定工作模式，也可實現不同工作狀態間的切換。通過控制開關L(=1，2，3)的通斷時間，模擬脈沖負載的周期和占空比，改變負載電阻L(=1，2，3)大小可以實現不同功率的負載。

2.3 脈沖負載仿真模型分析

在有關脈沖負載結構的研究中，文獻[13]對比了三相橋式相控整流器的等效拓撲結構和三相不控整流器級聯PI控制DC/DC變換器的等效拓撲結構，后者的直流電壓波動較小且脈沖負載消耗的有功功率的波形也更加穩定。因此本文采用三相不控整流器級聯PI控制DC/DC變換器的等效拓撲結構對脈沖負載結構進行仿真模型的搭建，其仿真模型電路如圖4所示。

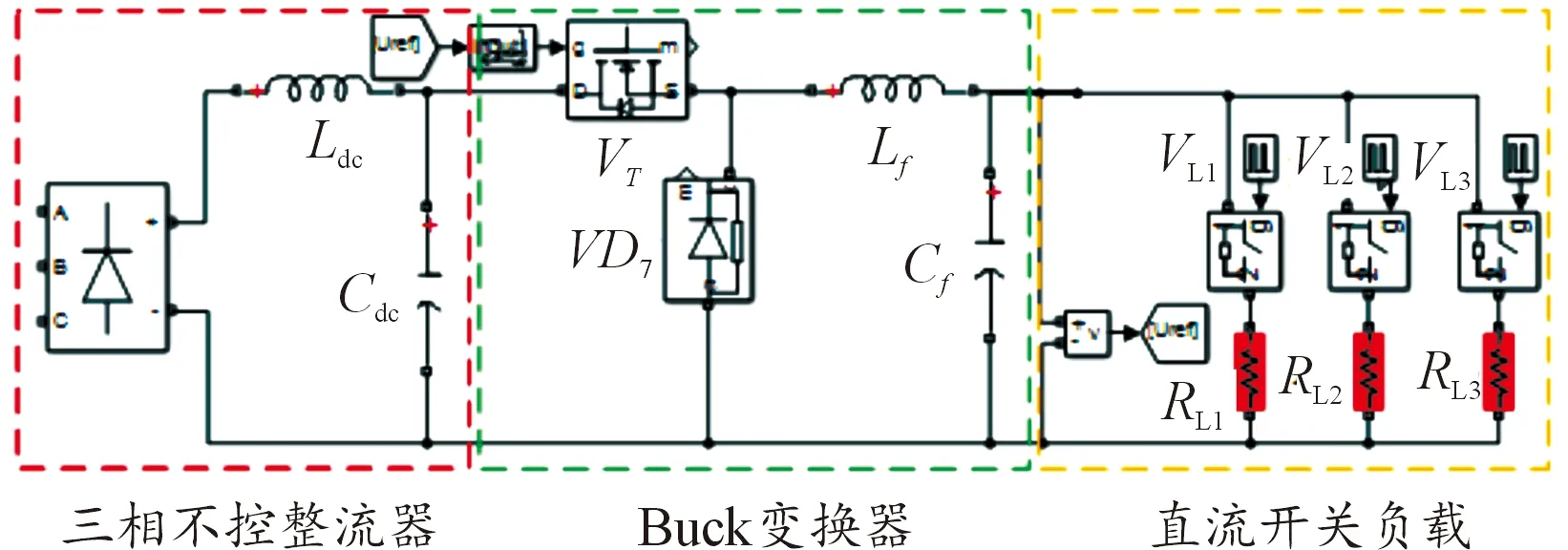
圖4 脈沖負載仿真模型電路圖

圖4中的脈沖負載仿真模型由不空整流器、濾波單元、DC/DC變換單元以及直流負載單元組成。柴油發電機組輸出交流電經過三相橋式整流器為脈沖負載供電，其不控整流器由6個型號規格相同的整流二極管組成，電感和電容對整流后的輸出電壓進行濾波，然后再通過Buck變換器，對濾波后的電壓進行穩壓，而后向直流開關負載供電。圖中，通過設置脈沖信號的工作周期、占空比以及可變電阻的大小，可以得到不同參數的脈沖負載工作特性。Matlab/Simulink軟件具有圖形界面、運行仿真方便的優點，通過仿真測試可以檢測所建立的模型的準確性。圖5為脈沖負載正常運行時的功率波形圖，從圖中可以明顯看出所搭建的脈沖負載可以達到預期目標。

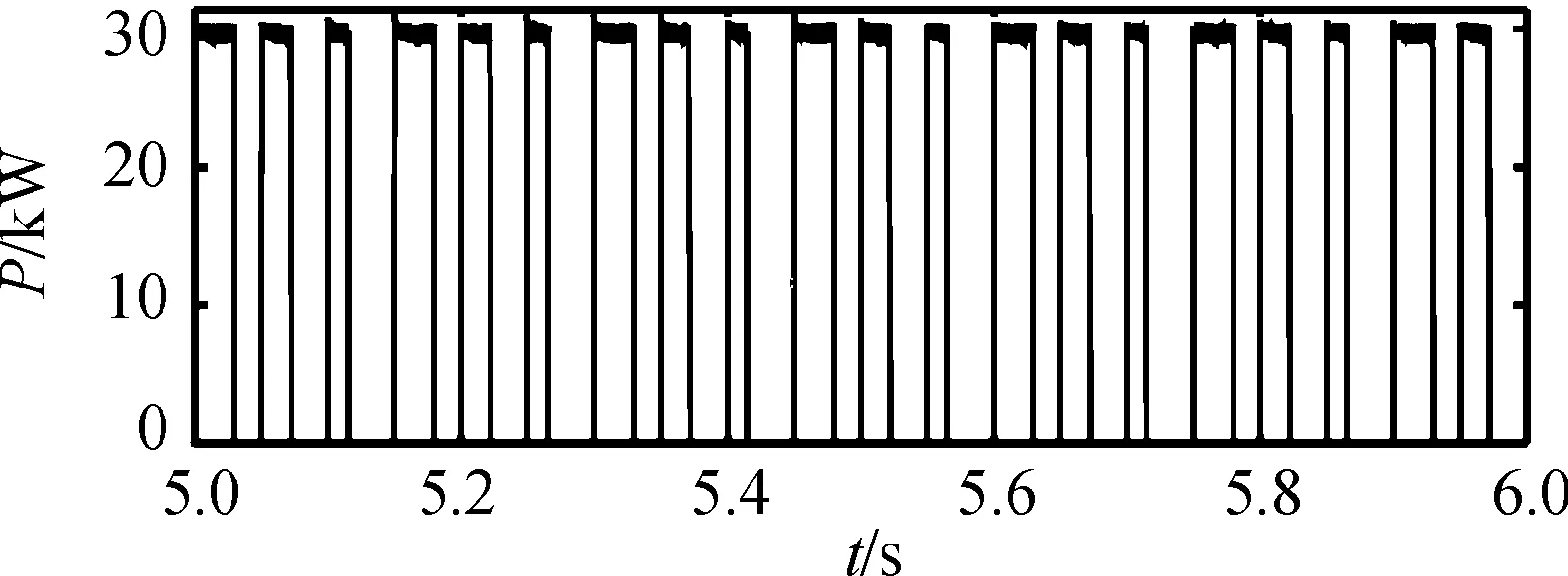
圖5 功率仿真波形圖

2.4 脈沖負載工作模式表述

脈沖負載電氣特性如圖6所示，圖中所示的脈沖負載是由重復的脈沖串組成，為脈沖負載的峰值功率，為脈沖負載的平均功率，為脈沖負載周期，為脈沖串內單個脈沖的周期，一般為幾毫秒到幾百毫秒，其關系為=3，、和分別是脈沖串內單個脈沖的占空比，和兩者關系由式(2)給出。為了方便描述脈沖負載的工作模式，本文采用PX(kW)-3TX(ms)-Dx_x_x(%)的表述方法，例如P30-3T20-D10_20_15表示峰值功率為30 kW，脈沖串周期為60 ms，脈沖串內有3個單脈沖周期為20 ms且占空比分別是10%、20%和15%工作模式的脈沖負載。

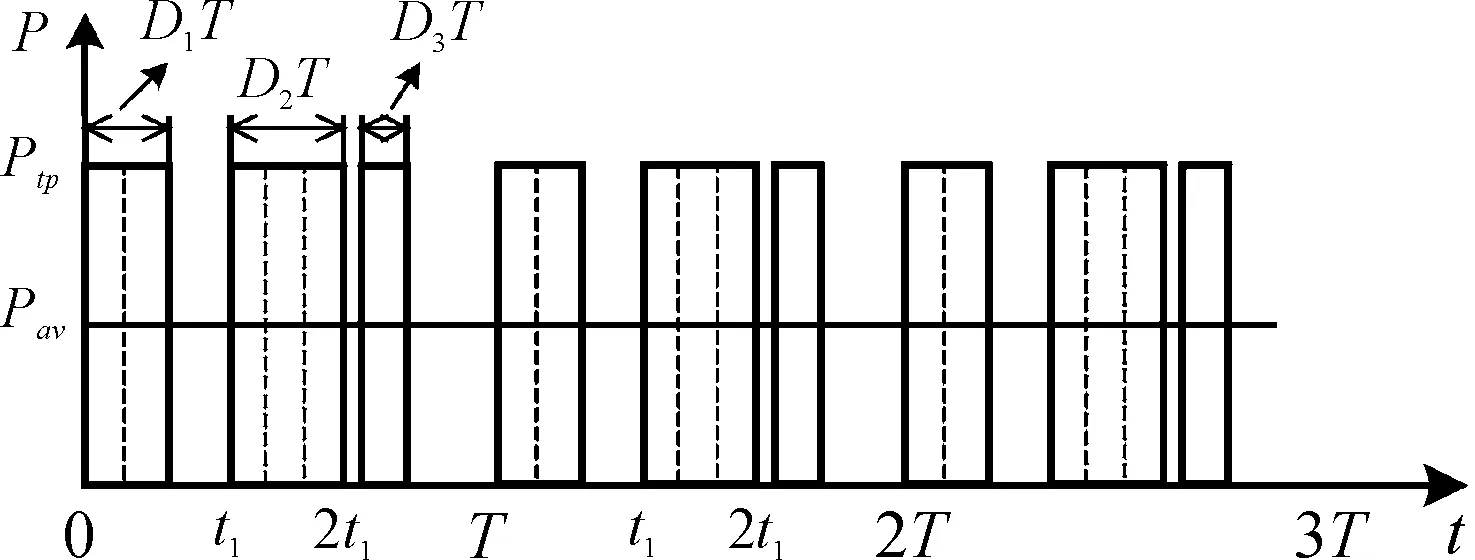
圖6 脈沖負載負荷電氣特性曲線

=(++)

(2)

3 脈沖負載參數對系統運行指標的影響變化

占空比、工作周期及峰值功率共同決定了脈沖負載的工作模式，這些參數的不同組合可以模擬現實中以現代相控陣雷達為代表的脈沖負載運行行為，因此下面針對脈沖負載的占空比、工作周期及峰值功率的變化來研究對柴油發電機組系統運行指標的影響，以此窺探出在柴油發電機系統中脈沖負載各參數的“影響力”大小。

3.1 峰值功率P對系統運行指標的影響

對供電系統來說，從能量角度看，不管是什么類型的負載，對其產生最大影響的因素始終是負載功率的大小，因此先研究分析峰值功率的改變對系統運行指標的影響。設置脈沖負載的工作模式為PX-3T30-P15_10_20，為每次仿真設置的功率值，逐步改變的值，分析峰值功率改變時系統各項運行指標的變化趨勢。

在占空比保持不變的情況下，當脈沖負載峰值功率增加時，從圖7(d)中可以看出，平均功率與峰值功率大致以線性關系增加，從時間軸上看，相當于脈沖負載增加了對能量的需求，在發電機額定容量不變的情況下，負重的增加會導致系統的穩定性下降。

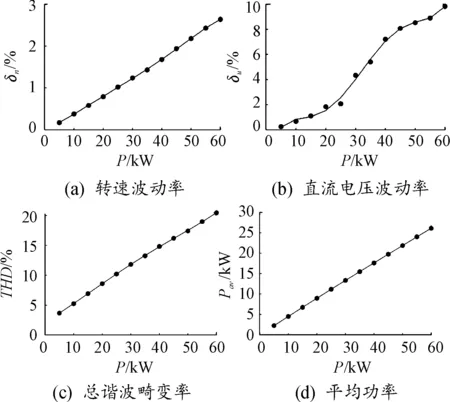
圖7 脈沖負載峰值功率變化時系統各運行指標變化規律曲線

從圖7中可以看出，轉速波動率和總諧波畸變率都隨著峰值功率的增加以近似線性關系增加，說明隨著峰值功率的增加，系統的轉速穩定性在變差的同時系統三相電壓中的諧波含量也在增加。從圖7(b)中可知直流電壓波動率也在隨著峰值功率的增加而增加，且在峰值功率為25～45 kW段內時，直流電壓波動率增加的速度比較快。

當峰值功率為50 kW時，系統的穩定性已經很差，轉速波動率達到了2.18%，而直流母線電壓波動率更是達到了8.53%，此時的供電質量已經不能滿足負載需求，而實際上脈沖負載的平均功率才只有21.876 kW，大約才占柴油發電機額定功率的43.75%，因此脈沖負載給柴油發電機系統的穩定運行帶來巨大挑戰。

3.2 工作周期T對系統運行指標的影響

上一節針對脈沖負載峰值功率改變時對系統運行指標的影響進行了分析，當峰值功率為30 kW時，柴油發電機系統已經受到了較為明顯的影響，但仍能工作，因此本節將脈沖負載的峰值功率設置為30 kW，占空比與上一節相同，改變工作周期，分析脈沖負載工作周期變化時系統各運行指標的變化規律。

從圖8(a)中可知，脈沖負載工作周期的改變對于轉速波動率的影響比較大，隨著脈沖負載工作周期的增加轉速波動率一直處在增大狀態。在工作周期變化時，直流電壓波動率圖8(b)變化較大，且工作周期為20 ms以前的變化范圍較廣，在20 ms后總體保持動態穩定，變化范圍不大，與脈沖負載平均功率圖8(c)的變化趨勢保持一致。結合測試數據可知，工作周期為1 ms時的直流電壓平均值為349.46 V，工作周期為60 ms時的直流電壓平均值為351.57 V，考慮到=，工作周期為1 ms時的平均功率應小于60 ms時的平均功率，但在圖8(c)中可知，60 ms時的平均功率卻小于1 ms時的平均功率，圖8(e)和(f)分別是脈沖負載工作周期為1 ms和60 ms時的功率波形圖，對比兩圖可知60 ms時的功率波形波動范圍更廣，與圖(b)直流電壓波動率中的結果一致，則在工作周期為1 ms和60 ms時的直流母線電壓存在式(3)的關系：

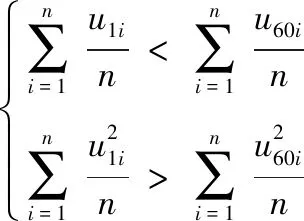
(3)

式中，和分別表示工作周期為1 ms和60 ms時的直流母線電壓，為選取采樣周期中含有的采樣點數。

由于脈沖負載的特殊性，使得三相電壓波形中含有大量的間諧波，而計算總諧波畸變率時，只計算了整數次諧波占基波的比重，并未考慮間諧波的影響。由于本文重點關注的是轉速的變化，因此THD指標變化趨勢同樣可以反映脈沖負載對系統交流電壓的影響，觀察圖8(d)可知，在工作周期為40 ms以前整數次諧波含量增加的比較快，而在40 ms以后，整體維持在12%左右波動，沒有出現大范圍的波動，說明工作周期的改變不是引起三相電壓畸變的主要因素。

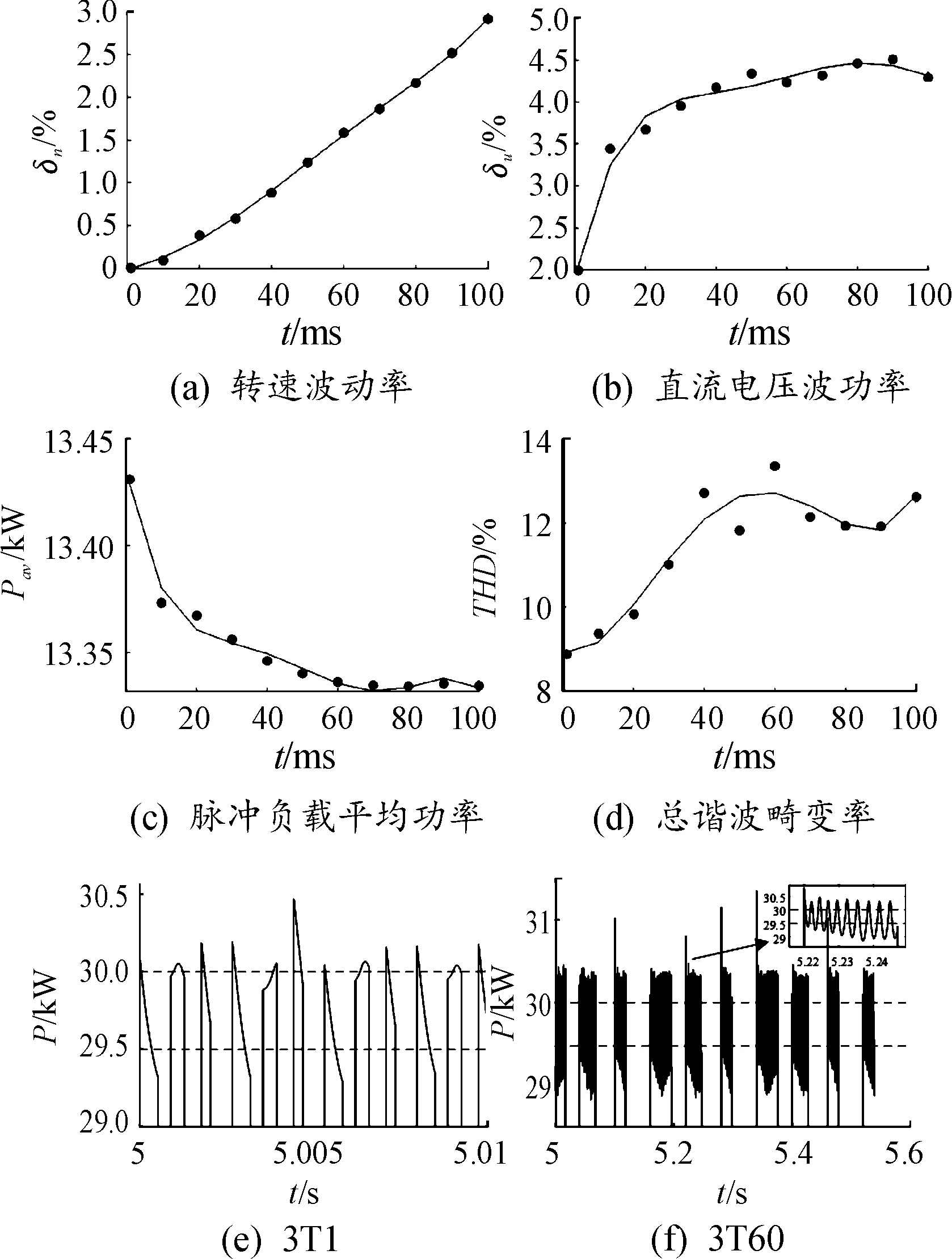
圖8 脈沖負載工作周期變化時系統各運行指標變化規律曲線

3.3 占空比D對系統運行指標的影響

由于本文中所建立的脈沖負載是由脈沖串組成，脈沖串中包含3個單脈沖，因此占空比就由3個分占空比、和組成且有如式(4)的取值限制。結合前兩節的分析，設置脈沖負載的工作模式為P30-3T50-DX_X_X，改變占空比的大小組合，得到不同工作模式下的系統各運行指標。由于占空比是由3個分占空比組成，因此有很多的組合方式，為了研究哪一種類型的組合方式對柴油發電機系統的影響最嚴重，將組合方式分為8種。以“1”、“2”、“3”依次表示單脈沖的寬度，“1”為最窄，“3”為最寬，則脈沖串有8種表示方式，分別為“123”、“321”、“212”、“121”、“132”、“231”、“312”和“213”，如圖9所示。

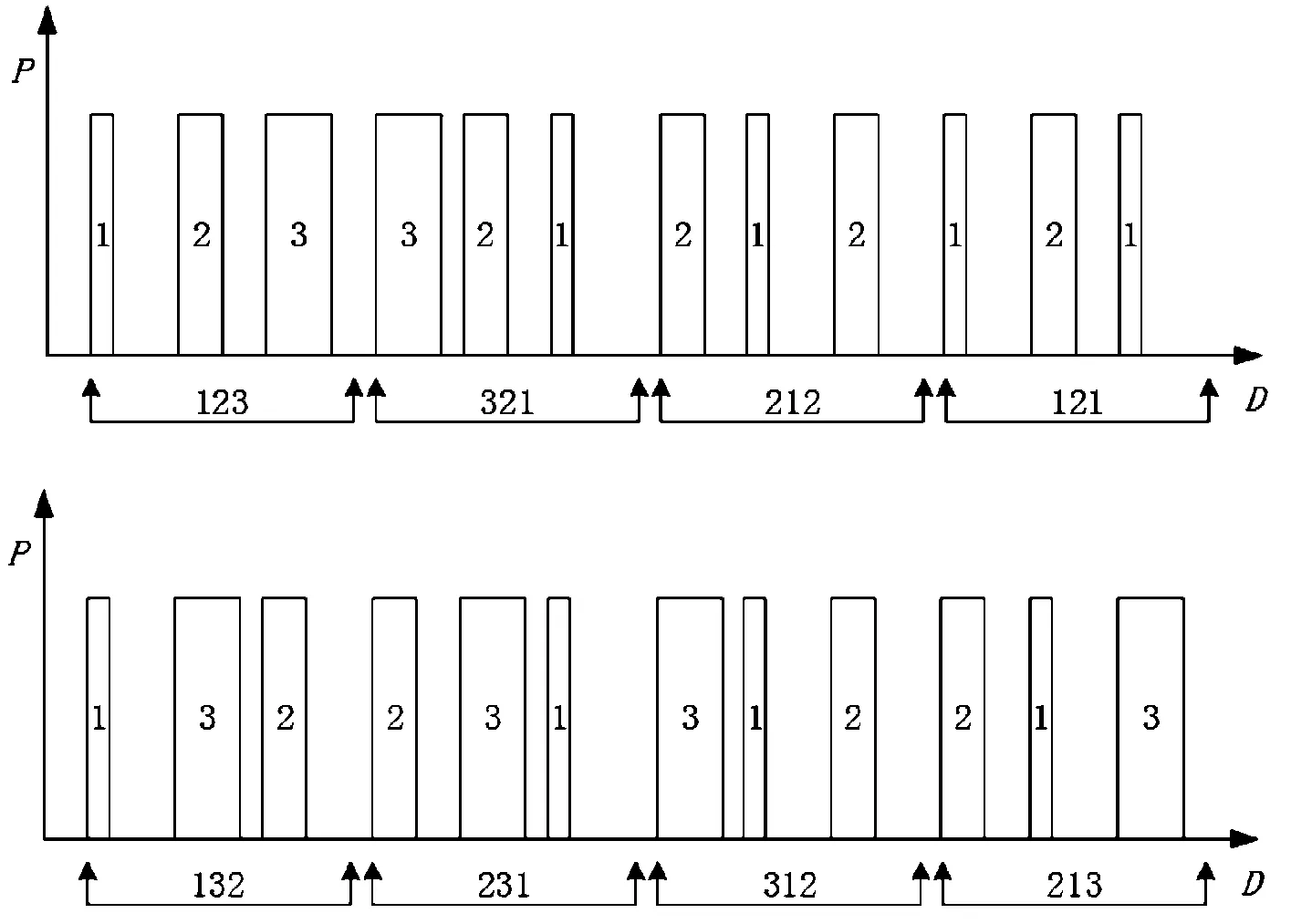
圖9 不同占空比的組合方式示意圖

考慮到式(4)對占空比的取值限制和測試數據時數據量的可測性，以3%為間隔，進行仿真測試。特別說明，由于占空比由3個部分組成，因此在作圖分析時，取三者的平均值作為橫軸。

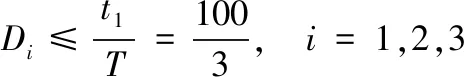
(4)

觀察圖10(a)可知，在“123”的不同組合中，“321”、“132”和“213”的轉速波動率比較相近，而“123”、“312”和“231”組合的轉速波動率比較相近，但是前者組合的轉速波動率整體要大于后者，說明前者組合的工作模式對于柴油發電機系統轉速影響比較大。圖10(b)中的“121”和“212”組合的轉速波動率在占空比的平均值Dav為20ms之前時，“212”組合的轉速波動率比較大，在20 ms之后，則“121”組合的值比較大，但總體趨勢與數值相差不大。

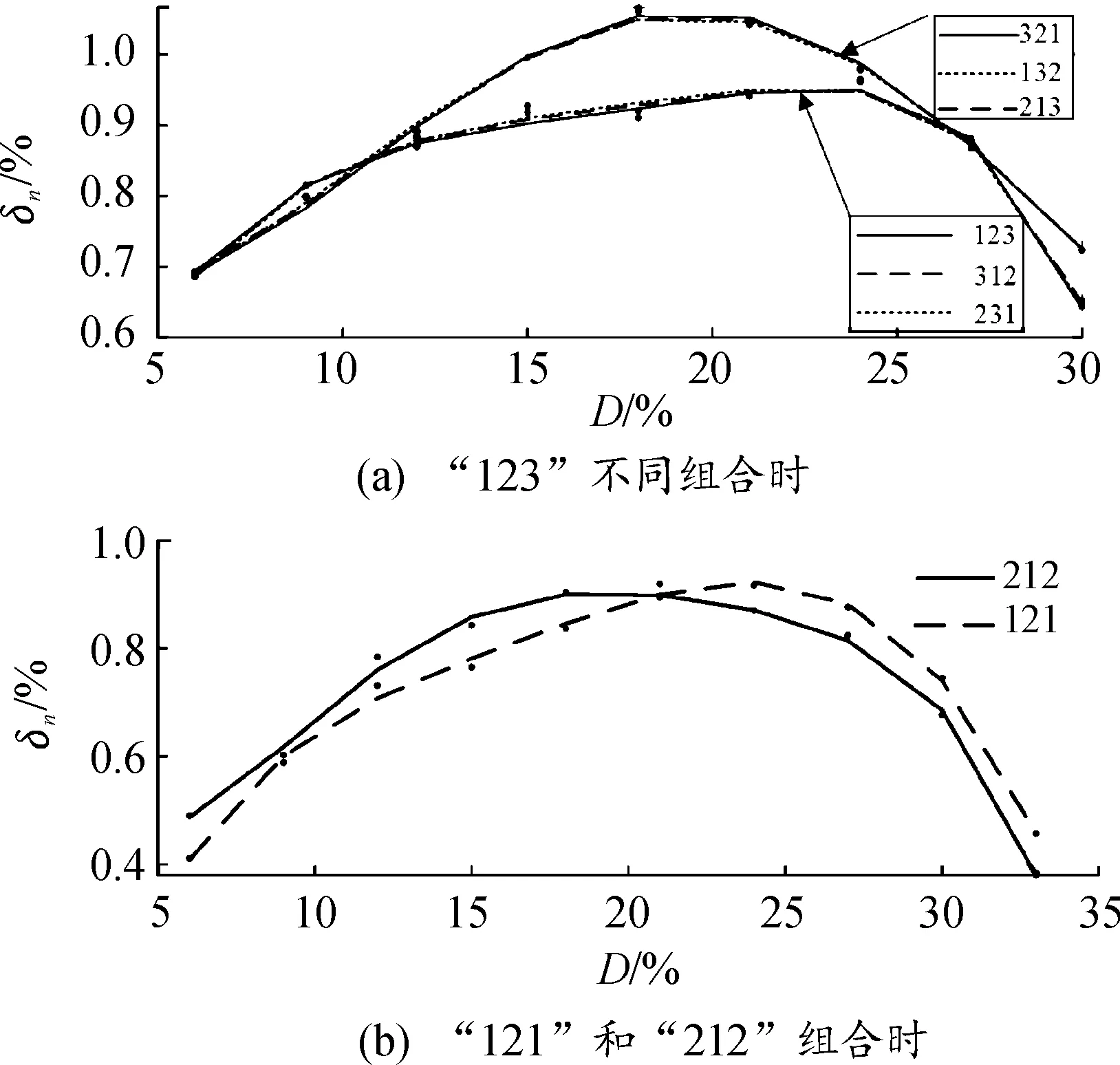
圖10 不同占空比組合時轉速波動率曲線

在分析圖10中的轉速波動率時，圖10(a)中的值明顯大于圖10(b)中的值，當占空比不同時，會造成脈沖負載的平均功率不同，從能量的角度看，在相同的工作時間內，圖10(a)中所代表工作模式的脈沖負載所消耗的能量大于圖10(b)所代表的脈沖負載。如圖11所示，不同占空比工作模式下脈沖負載的平均功率，圖中黑色線條代表“123”組合脈沖負載的平均功率線，由于6種工作模式的平均功率基本相等，因此平均功率線條在圖中重合為一條黑色線條，而“212”組合的脈沖負載平均功率比“123”組合的平均功率小，比“121”組合的平均功率大。再結合圖10的轉速波動率值分析，考慮是否由于“121”和“212”組合的平均功率小，同等時間內消耗的能量比較小，因此使得柴油發電機系統的轉速波動率比較小。基于此問題，又設計了仿真實驗，保持“121”和“212”的工作模式不變，但使重新設置的脈沖負載平均功率與“123”組合基本一致，得到圖12所示的新工作模式下轉速波動率與平均功率對比圖。

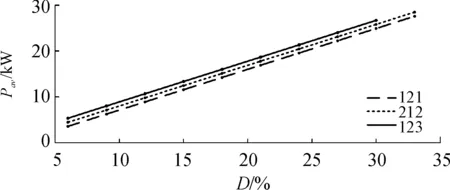
圖11 不同占空比組合時脈沖負載的平均功率曲線

在圖12(a)中曲線L3和L4是新工作模式下的轉速波動率的曲線，L1和L2是原曲線，從圖中可以看出4條曲線的整體趨勢與大小區別不大，但是在圖12(b)平均功率曲線圖中，可以明顯看出新工作模式下的平均功率曲線L3明顯大于原曲線L1和L2，說明在“121”和“212”的工作模式下，脈沖負載對柴油發電機系統的轉速影響要小于“123”組合下的脈沖負載，而在“123”的組合方式中，“321”、“132”和“213”組合下的脈沖負載對柴油發電機系統的轉速影響最嚴重。圖13是所有工作模式下的總諧波畸變率曲線，由于所有曲線的趨勢相同，因此并未在圖中標注哪一條曲線代表哪一種工作模式，從圖中可以明顯看出隨著占空比的增加總諧波畸變率隨之增加。

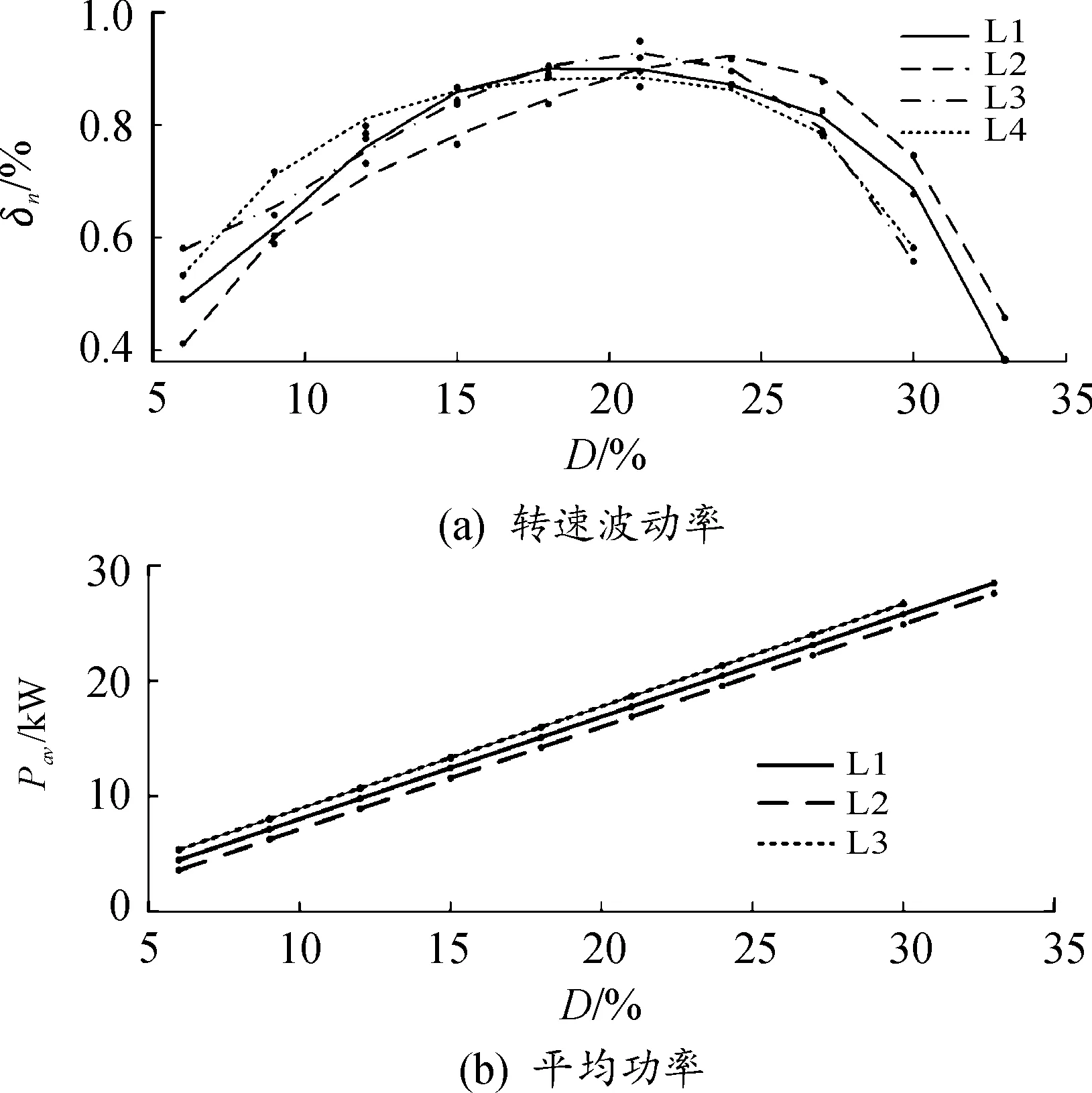
圖12 新工作模式下轉速波動率和平均功率曲線

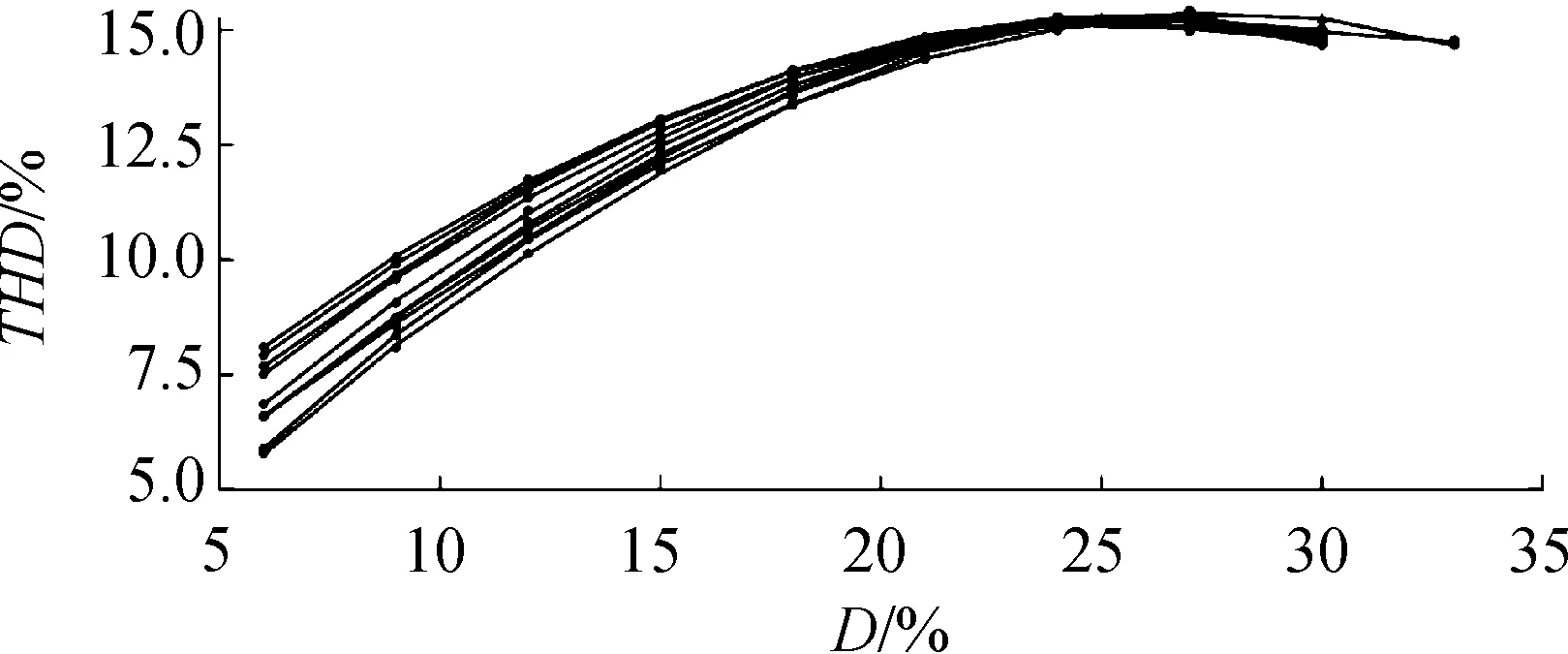
圖13 所有工作模式下的總諧波畸變率曲線

綜上分析可知，脈沖負載的占空比、工作周期及峰值功率共同決定了脈沖負載的工作特性，對柴油發電機組的平穩運行造成了較為嚴重的影響。

4 結論

1)隨著脈沖負載功率和工作周期的增加，柴油發電機的轉速波動率近似線性增加，而不同占空比組合對柴油發電機轉速影響程度不同，其中“321”、“132”和“213”組合的影響最大，且隨著占空比的增加，轉速波動率先增加后減小，在占空比平均值為18%左右時達到最大值。

2)電壓總諧波畸變率隨著脈沖負載功率的增加近似線性增加；隨著工作周期的增加，先快速增加到某個值后上下跳動；隨著占空比平均值的增加，以加速度逐漸減小的速度增加，在達到某個值后保持基本不變。