內嵌PMI泡沫的CFRP方形蜂窩夾芯動態壓縮特性數值仿真

周 昊，郭 銳，姜 煒

(1.南京理工大學 化學與化工學院，南京 210094；2.南京理工大學 機械工程學院，南京 210094)

1 引言

夾芯是夾層結構的主要吸能部件，對夾層結構的整體性能具有關鍵作用。設計并研究質量輕、吸能效率高的夾芯結構一直是防護結構領域的研究熱點。近年來，纖維增強復合材料憑借其優異的性能在夾芯構型中得到了廣泛應用，國內外學者提出了大量基于纖維增強復合材料的夾芯構型，如蜂窩、波紋以及點陣結構等，并對其力學性能進行了研究。

為了進一步提升夾芯的吸能特性，向蜂窩等薄壁結構中填充輕質泡沫材料為提升夾芯結構的吸能效率提供了新的思路。Reddy等研究了填充PU泡沫的薄壁圓管結構的軸向壓縮特性，發現泡沫填充體能夠有效提高結構的吸能特性。Wu等通過向蜂窩中填充PU泡沫來改善結構的力學性能，其研究結果表明，由內嵌泡沫蜂窩作為夾芯的夾層結構具有更好的抗沖擊特性。Mozafari等通過試驗和數值仿真分析了內嵌泡沫對蜂窩結構的壓縮強度及能量吸收特性等面內壓縮性能的影響，證明了內嵌泡沫能夠顯著提高蜂窩的強度和吸能特性。Hussein等通過準靜態壓縮試驗分析了內嵌PU泡沫和鋁蜂窩的方形鋁管的壓縮特性，發現內嵌結構改變了鋁管的失效模式，提高了結構的比能量吸收。Liu和Zhang等分別研究了EPP泡沫填充體對蜂窩結構在準靜態和動態壓縮載荷作用下力學性能的影響。

聚甲基丙烯酰亞胺(polymethacrylimide，PMI)泡沫作為一種新型輕質、高性能結構泡沫材料，具有力學性能優異、閉孔率高、易粘接、易加工等優點，在夾層結構夾芯中具有較好的應用前景。目前對于PMI泡沫夾層結構力學性能及耐撞吸能方面的研究已有所開展，但關于內嵌PMI泡沫混雜夾芯動態壓縮特性相關研究較少，因此PMI泡沫夾芯的動態壓縮響應特性不明確，阻礙了其進一步工程應用。

本文在在研究內嵌PMI泡沫的CFRP方形蜂窩夾芯準靜態壓縮特性的基礎上，進一步分析夾芯的動態壓縮特性，分析了夾芯在不同應變率加載下的響應特性，研究了不同結構參數對其動態壓縮特性的影響規律，并構建了夾芯動態壓縮強度與應變率間的關系，研究結果能夠為此類夾芯在抗爆抗沖擊結構中的應用奠定研究基礎。

2 數值仿真建模

本文所研究的內嵌PMI泡沫的CFRP方形蜂窩夾芯結構如圖1所示，其中方形蜂窩結構由厚度為的2×2斜紋編織CFRP材料制成，其密度為1 450 kg/m，彈性模量為4.8 GPa。PMI泡沫內嵌于方形蜂窩結構空腔中。夾芯相對密度為：

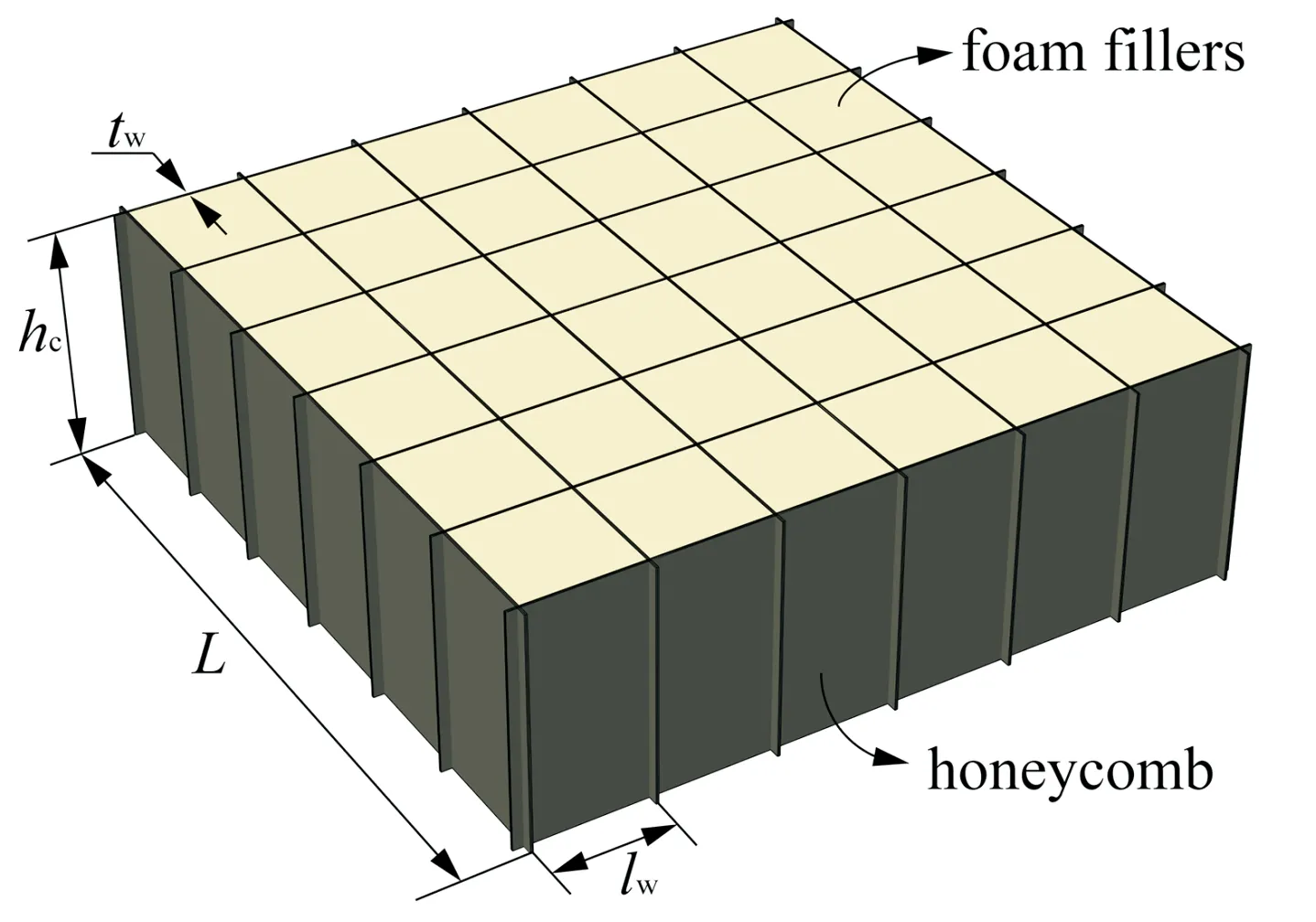
圖1 內嵌PMI泡沫的CFRP方形蜂窩夾芯結構示意圖Fig.1 Illustration of the square CFRP honeycomb with PMI foam fillers

(1)

利用ABAQUS建立如圖2所示的夾芯動態壓縮數值仿真模型，其中蜂窩結構通過四節點殼單元(S4R)進行離散，內嵌泡沫通過八節點實體單元(C3D8R)進行離散，通過單元尺寸敏感度分析確定單元尺寸約為蜂窩柵格間距的十分之一(/10)。剛性薄板設置于夾芯上下表面，并與夾芯接觸面固連，通過薄板位移載荷實現對夾芯結構的動態壓縮。

圖2 夾芯動態壓縮數值仿真模型示意圖Fig.2 Numerical model

選取Hashin損傷模型描述CFRP材料的損傷演化過程。模型考慮了4種失效模式：① 纖維拉伸斷裂；② 纖維壓縮屈曲及扭結；③ 基體橫向拉伸及剪切條件下裂紋；④ 基體橫向壓縮及剪切條件下破碎。相關材料參數通過材料靜態力學性能試驗獲得，CFRP材料模型主要參數如表1所示。

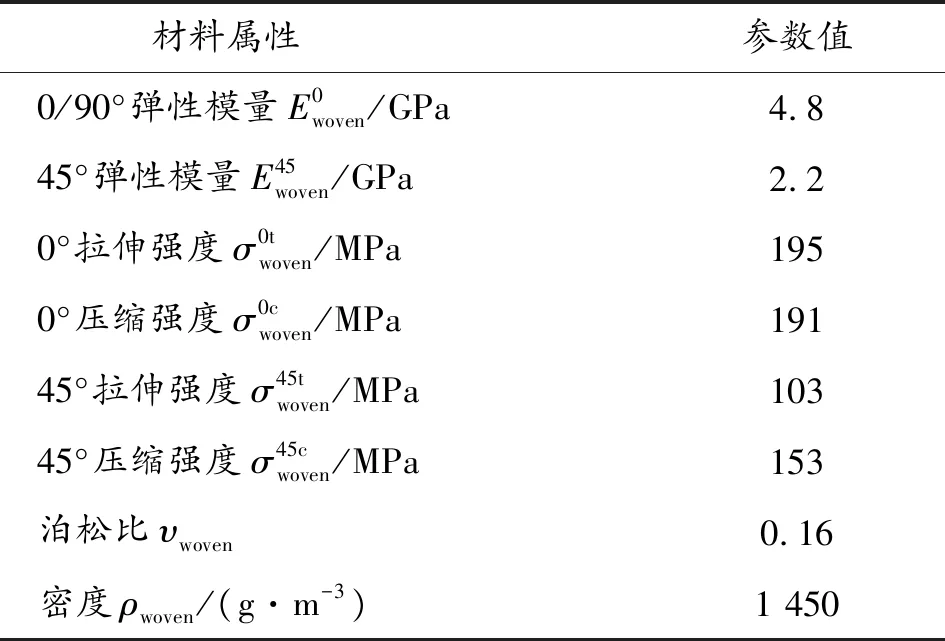
表1 CFRP材料參數Table 1 Material parameters of CFRP

對于內嵌PMI泡沫材料則選用可壓縮泡沫模型(Crushable foam)進行描述，同時考慮泡沫材料的應變率效應，并通過準靜態材料力學性能試驗對泡沫材料的模型參數進行標定，文中所用PMI泡沫材料主要參數如表2所示。

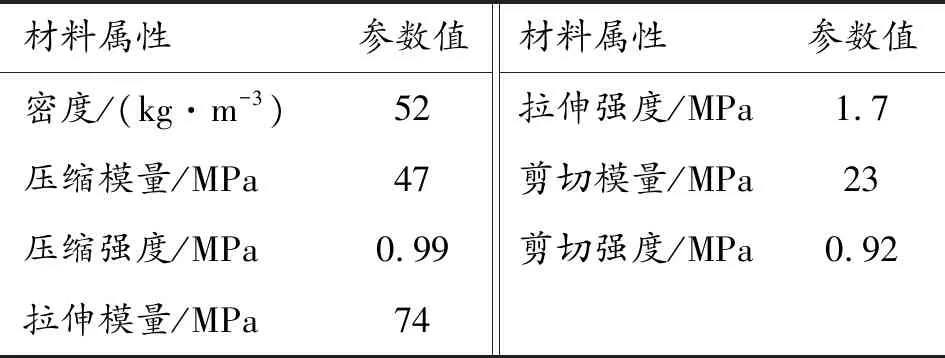
表2 PMI泡沫材料參數Table 2 Materials parameters of PMI foam

3 仿真結果分析與討論

3.1 不同應變率下夾芯動態壓縮特性

通過數值仿真對了不同應變率條件下夾芯的動態壓縮過程進行了模擬，首先分析了蜂窩柵格間距為=20 mm，夾芯高度為=2的夾芯在不同應變率條件下的壓縮特性，應變率分別為50 s、100 s、200 s和500 s。夾芯不同應變率下的應力和比能量吸收隨名義應變的吸收情況分別如圖3和圖4所示。

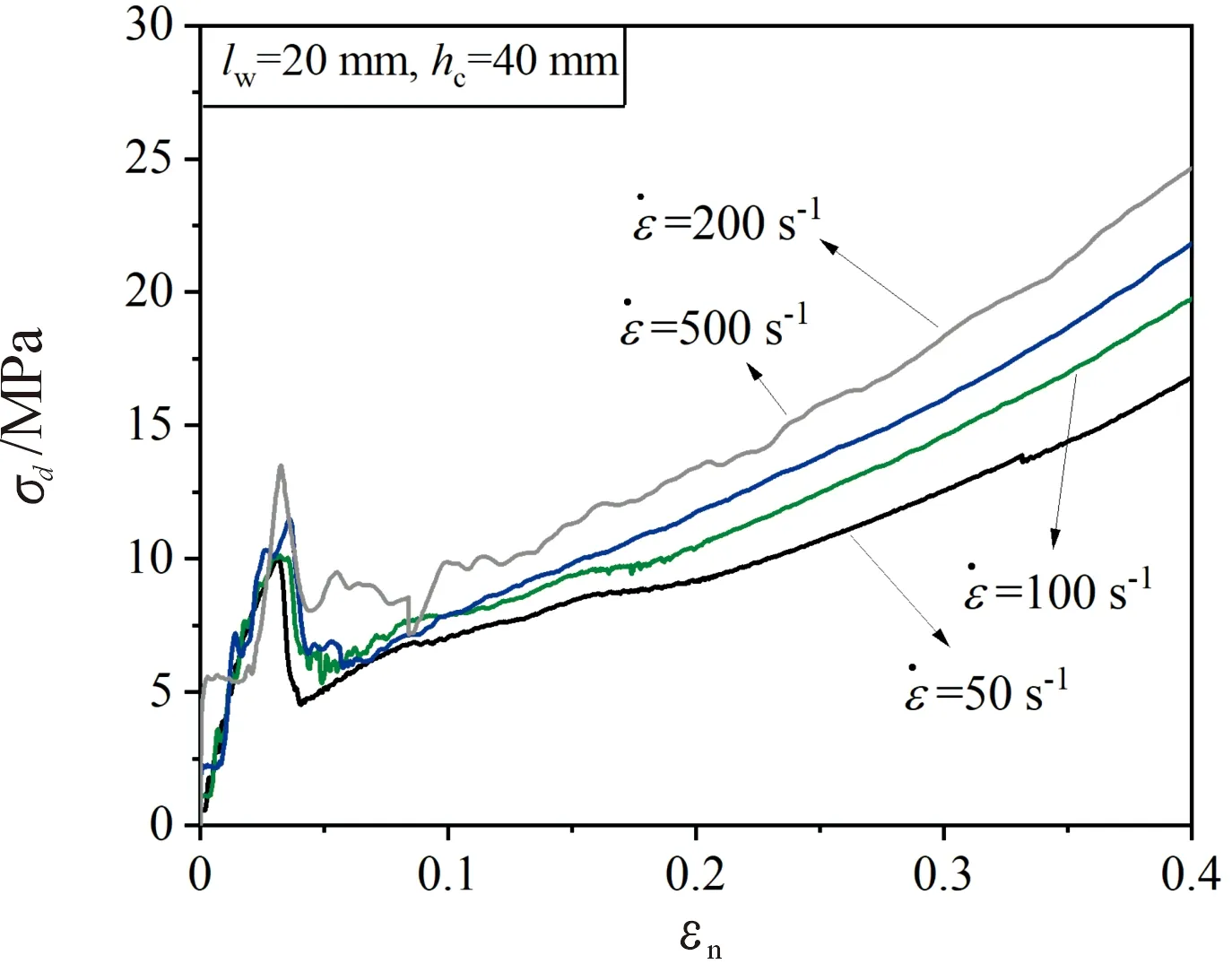
圖3 lw=20 mm，hc=40 mm的夾芯在不同應變率下的應力應變曲線Fig.3 Stress versus strain curves of the core with lw=20 mm and hc=40 mm under different strain rates

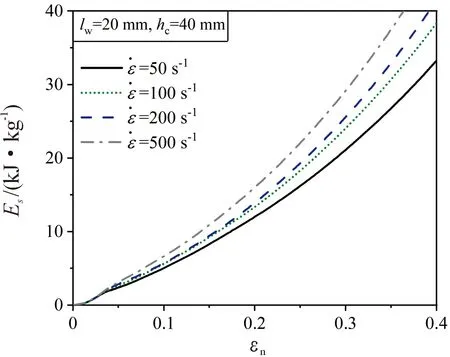
圖4 lw=20 mm，hc=40 mm的夾芯在不同應變率下的比能量吸收曲線Fig.4 Specific energy absorption of the core with lw=20 mm and hc=40 mm under different strain rates

通過圖3可以看出，對于=20 mm的夾芯，在動態壓縮載荷下，其應力應變響應可分為彈性段、屈曲段、失效段以及失效后的應力強化段，而沒有明顯的應力平臺段。通過圖4可以看出，隨著應變率的增大，夾芯中的應力水平不斷增大，其比能量吸收也不斷增加。

3.2 夾芯結構參數對其動態壓縮特性影響分析

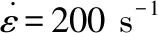
圖5 不同蜂窩柵格間距的夾芯在應變率時的動態壓縮應力應變曲線Fig.5 The dynamic compressive stress versus strain curve of cores with different lw under strain rate of s-1

通過圖5可以看出，隨著蜂窩柵格間距的增大，夾芯的強度降低，因此其壓縮模量不斷減小，壓縮應力也逐漸減小。當蜂窩柵格間距較小時，夾芯動態壓縮強度較高，因此壓縮失效后夾芯應力會大幅度下降；隨著蜂窩柵格間距的不斷增大，夾芯在壓縮失效后的應力下降幅度不斷減小，應力強化段的應力水平也逐漸趨于一致。通過圖6中不同蜂窩柵格間距的夾芯動態壓縮比能量吸收情況可以看出，夾芯結構的比能量吸收能力隨著蜂窩柵格間距的增大而不斷減小。當=5 mm時，由于蜂窩結構的強度遠大于其他夾芯，蜂窩結構在壓縮破壞中吸收了大量的能量，因此此種夾芯的比能量吸收能力最強，且當名義應變>0.15后這種優勢愈加明顯；隨著蜂窩柵格間距不斷增大，夾芯的壓縮應力水平逐漸趨于一致，其壓縮比能量吸收能力不斷減小，但差距也在不斷縮小，當>20 mm后，夾芯的比能量吸收能力幾乎不再隨蜂窩柵格間距的增大而變化。

圖6 不同蜂窩柵格間距的夾芯在應變率時的動態壓縮比能量吸收曲線Fig.6 The specific energy absorption of cores with different lwunder strain rate of s-1

圖7所示為夾芯在不同應變率載荷下動態壓縮強度隨蜂窩柵格間距的變化關系，同時加入了夾芯準靜態壓縮強度作為對比。通過圖7可以發現，隨著蜂窩柵格間距的增大，夾芯結構的動態壓縮強度近似呈指數形式衰減。這是由于蜂窩結構的壓縮強度隨其柵格間距的增大不斷減小，因此夾芯的整體壓縮強度隨蜂窩柵格間距的增大逐漸由蜂窩結構強度主導轉變為泡沫材料強度主導。

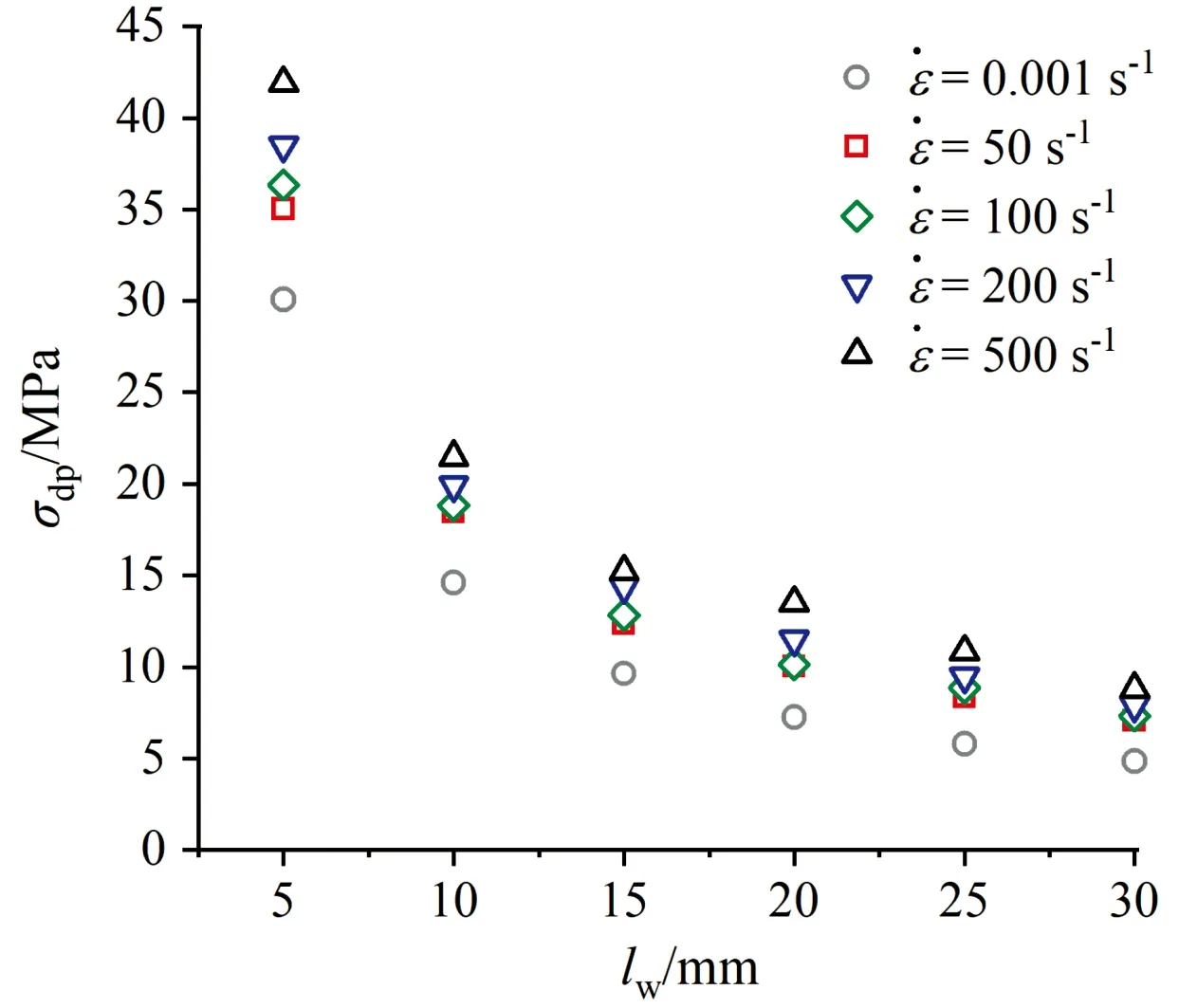
圖7 夾芯結構在不同應變率下動態壓縮強度隨蜂窩柵格間距的變化關系示意圖Fig.7 The dynamic compressive strength of the core with different lw under different strain rates

進一步對比可以發現，夾芯結構在動態壓縮載荷下的壓縮強度相比于準靜態壓縮有了較大的提升，且隨著應變率的增大，夾芯結構的動態壓縮強度也不斷增大，說明夾芯在壓縮過程中存在應變率增強效應，且隨著應變率的增大，這種增強效應也愈加明顯。

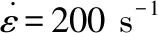
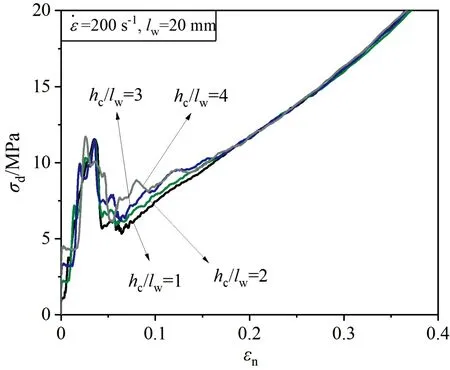
圖8 不同高度的夾芯在應變率時的動態壓縮應力應變曲線Fig.8 The dynamic compressive stress versus strain curve of cores with different hc under strain rate of s-1

圖9 不同高度的夾芯在應變率時的動態壓縮比能量吸收曲線Fig.9 The specific energy absorption of cores with different hc under strain rate of s-1

圖10所示為夾芯結構在不同應變率條件下的動態壓縮強度隨夾芯高度的變化關系，可以看出，隨著夾芯高度的增大，其動態壓縮強度在不同應變率下的變化幅度均較小，且沒有明顯的變化規律，這說明夾芯高度對其壓縮強度的影響較小。對比不同應變率下的夾芯壓縮強度可以發現，夾芯的動態壓縮強度與準靜態壓縮強度相比有了較大提升，且隨著應變率的增大，夾芯結構的動態壓縮強度也不斷增大。

圖10 夾芯結構在不同應變率下動態壓縮強度隨夾芯高度的變化關系示意圖Fig.10 The dynamic compressive strength of the core with different hc under different strain rates

3.3 夾芯動態壓縮強度與應變率間的關系

通過上述研究發現，夾芯結構的動態壓縮強度與應變率之間存在一定的關系，為了得到夾芯結構動態壓縮強度與壓縮應變率之間的定量關系，首先計算得到了夾芯在動態壓縮載荷和準靜態壓縮載荷下應力之間的比值()，其隨夾芯壓縮塑性應變之間的關系如圖11所示。通過圖11可以看出，夾芯動態壓縮與準靜態壓縮載荷下的應力比值隨壓縮塑性應變的增大呈現出不斷增大的趨勢，但增大速率隨塑性應變的增大不斷減小，因此應力比值逐漸趨于平穩。通過對比還可以看出，應力比值與塑性應變間的關系隨著壓縮應變率的增大呈現出相同的變化趨勢。

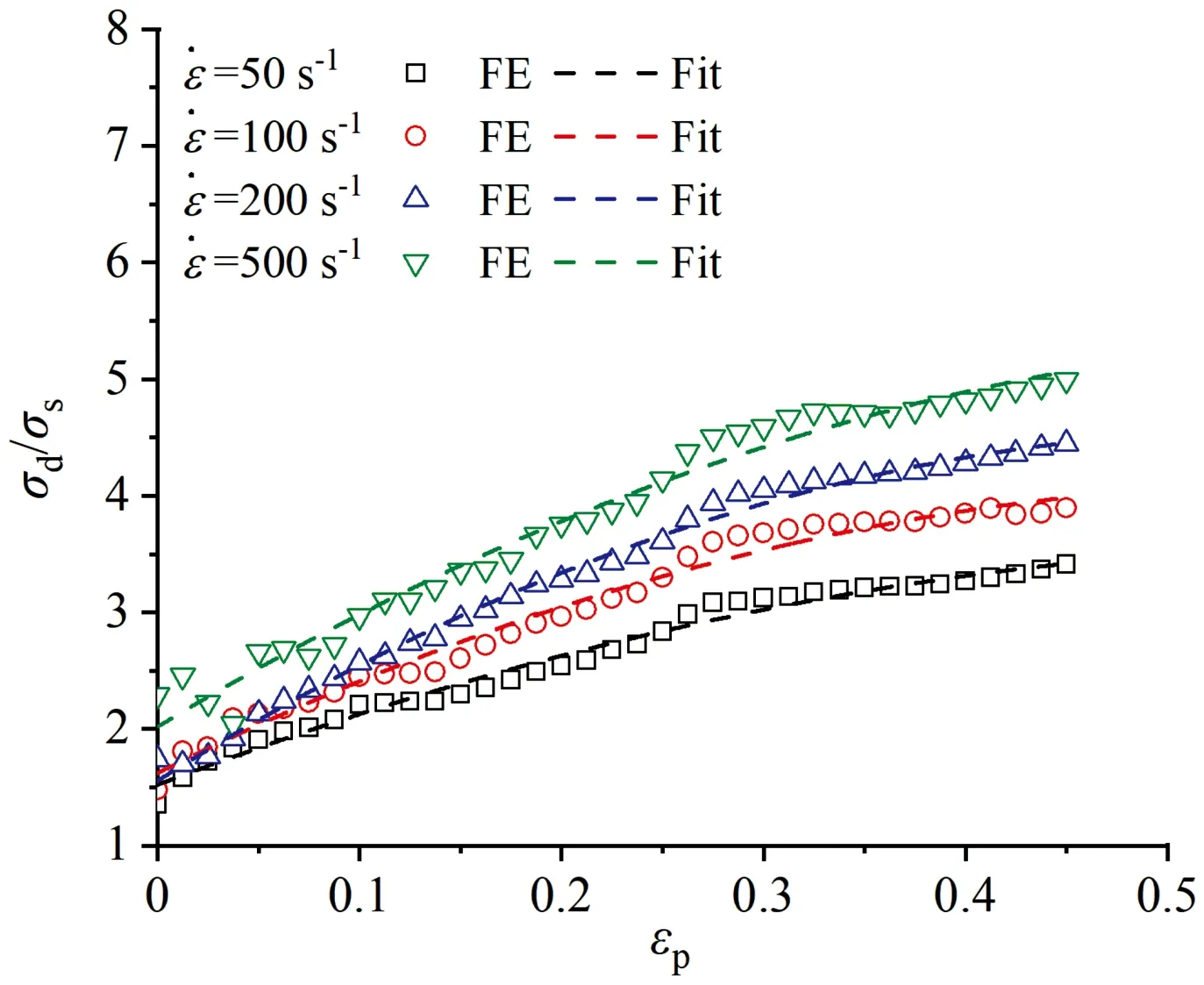
圖11 夾芯動態壓縮與準靜態壓縮載荷下應力比值與塑性應變關系曲線Fig.11 Relation of ratio of the compressive strength of the core under dynamic load to quasi static load with the plastic strain

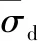
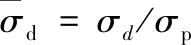
(2)

其中，為夾芯動態壓縮應力，為準靜態壓縮破壞強度。

通過計算，不同構型的夾芯在不同壓縮應變率下的歸一化動態壓縮應力與應變間的關系如圖12所示。

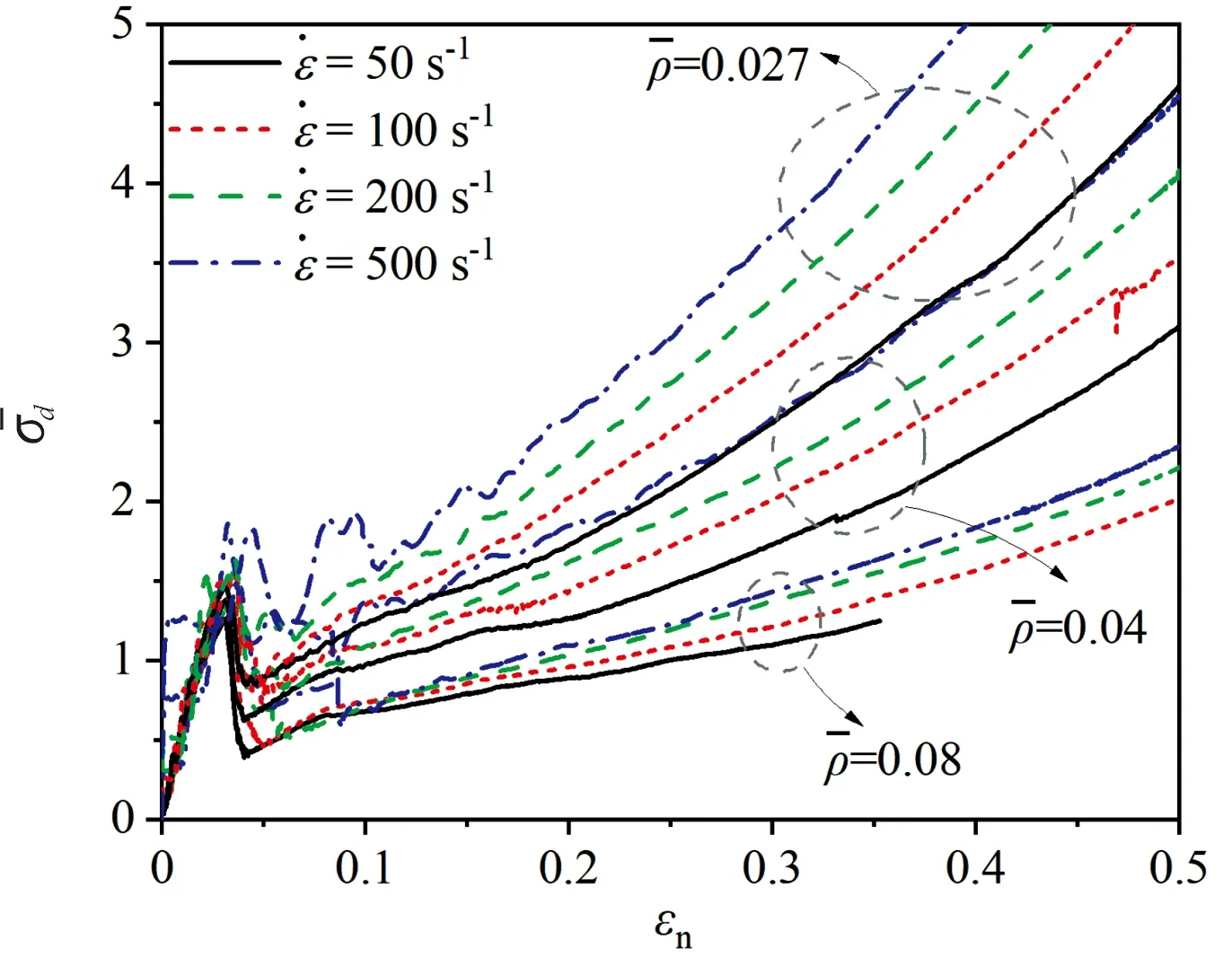
圖12 不同構型夾芯的歸一化動態壓縮應力應變曲線Fig.12 Relation between the normalized dynamic compressive stress and the compressive strain of different cores

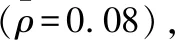
為了得到夾芯歸一化動態壓縮應力與應變率之間的關系，圖13給出了不同應變時夾芯的歸一化動態壓縮應力隨壓縮應變率之間的關系，為了更加清楚地表征應變率的變化，我們在此將壓縮應變率轉換為夾芯受到的壓縮速度，具體轉化關系為：

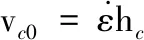
(3)

通過圖13可以看出，夾芯的歸一化動態壓縮應力與壓縮速度的對數呈線性相關，因此記：

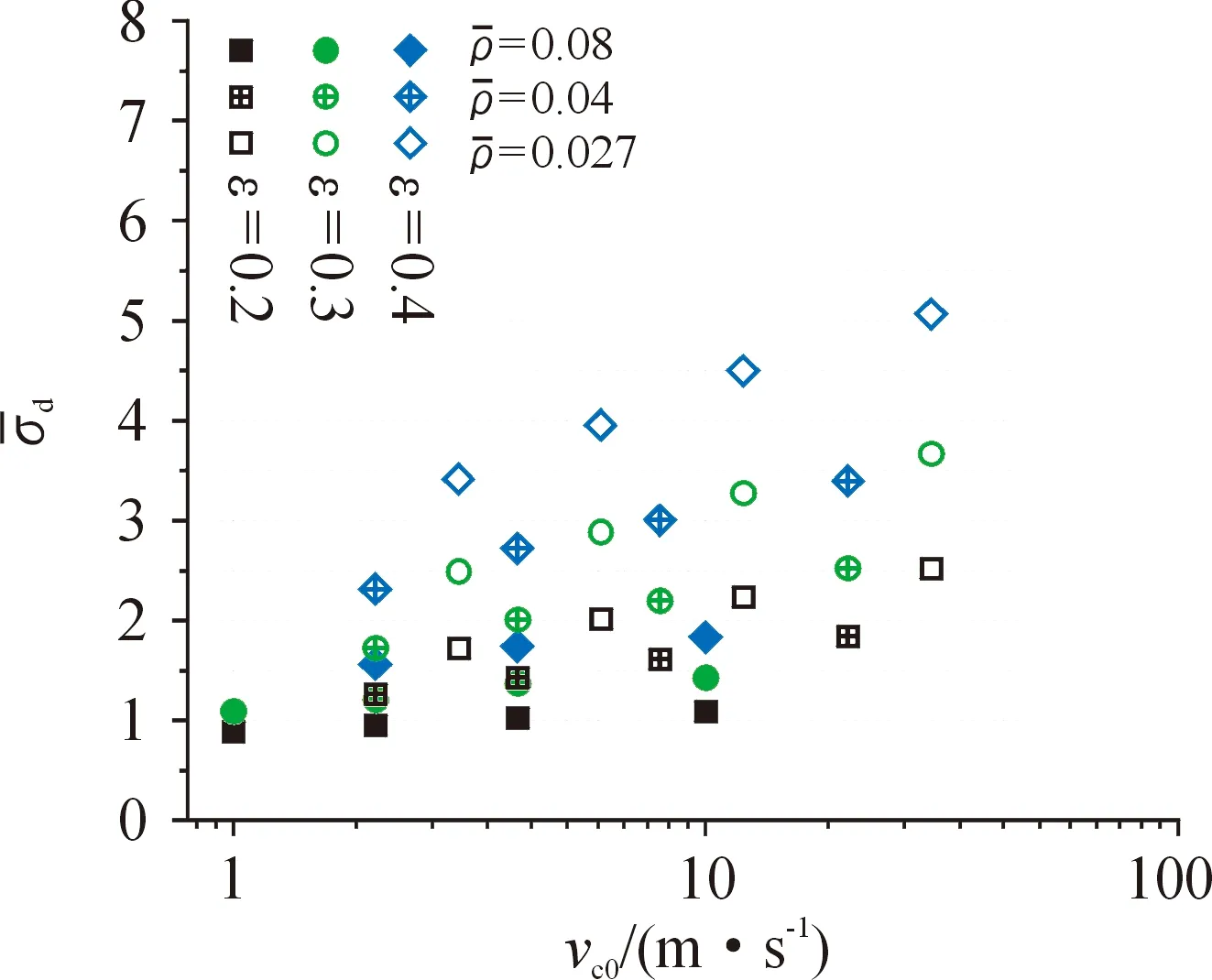
圖13 夾芯的歸一化動態壓縮應力與壓縮速度間的關系曲線Fig.13 Relation of the normalized dynamic compressive stress of the core with the compressive velocity

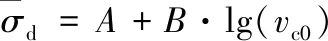
(4)

通過擬合可以得到不同夾芯相對密度及不同應變下系數、的值，通過進一步擬合可以得到系數、與夾芯相對密度和應變的具體關系為：

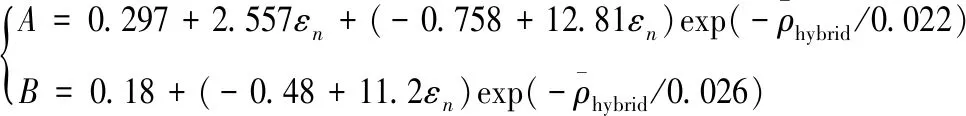
(5)

綜上即可根據式(2)、(3)和(4)對夾芯在不同應變率條件下的歸一化動態壓縮應力進行估算，不同應變率下相對密度為004的夾芯在不同壓縮應變時歸一化動態壓縮應力的仿真結果與估算值如表3所示。通過表3可以看出，各種情況下的估算誤差均小于5，說明上述擬合關系式的準確度較高，可以用于夾芯歸一化動態壓縮應力的估算。

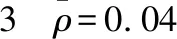
表的夾芯歸一化動態壓縮應力仿真值與估算值Table 3 Comparison between the numerical and predicted results of the normalized dynamic compressive strength of the core with relative density of

4 結論

1)內嵌PMI泡沫的CFRP方形蜂窩夾芯在動態壓縮過程中出現了應力增強現象，其應力應變響應可分為彈性段、屈曲段、失效段以及失效后的應力強化段，不存在應力平臺段。

2)隨著蜂窩柵格間距的增大，夾芯結構的動態壓縮強度近似呈指數形式衰減。隨著夾芯高度的增大，夾芯的動態壓縮強度在不同應變率下的變化幅度較小，說明高度對夾芯動態壓縮強度的影響較小。

3)夾芯動態壓縮強度與其準靜態壓縮強度和壓縮應變率之間存在定量關系，通過構建的預測模型可以預測夾芯在不同動態壓縮條件下的動態壓縮強度。