小學生數學問題解決過程的表現研究

溫明明

【摘要】研究小學生數學問題解決過程中的表現，可以幫助教師了解學生的知識掌握及能力發展狀況，以便教師不斷改進教學方案，進而增強教學效果。因此，研究小學生數學問題解決過程的表現至關重要。文章討論了研究小學生數學問題解決過程表現的必要性，分析了教師研究學生表現的方法。

【關鍵詞】數學教學；數學問題；解決過程；研究方法

【中圖分類號】G623.5【文獻標志碼】A【文章編號】1006—0463（2022）04—0112—04

從某種意義上來講，小學數學教育的本質就是培養學生解決數學問題的能力。實踐證明，在問題解決的過程中，學生能鞏固所學，同時也能訓練探究意識、思維能力、創新精神。其實，大多數學教師認識到學生經歷問題解決過程的必要性，但在分析學生表現、獲得反饋信息的過程中，由于缺乏科學、合理的量化方法，造成反饋信息不準確，影響了教師的判斷[1]。因此，研究小學生數學問題解決過程的表現至關重要。下面，筆者就如何研究小學數學問題解決過程的表現，談談自己的體會。

通過查閱大量的文獻資料后發現，小學數學教學中，目前大部分教師僅對學生解決問題的水平進行評估，且較多使用“好”、“不好”、“還行”、“還不錯”等進行評價，且這一判斷往往來自于教師的教學經驗。顯然，這樣判斷比較模糊，不能為教學方案的改進提供具體參考。本研究分析多種原因，得出了更為精準地判斷小學生數學問題解決現實表現的框架，從而更好地評估與判斷小學生解決數學問題的能力以及存在的問題，進而有針對性地提出改進方案，促進小學生解決數學問題能力的提升。

（一）分析設計的數學問題是否得當

首先，分析設計的問題是否符合學生成長階段的特征，是否結合教材內容以及新課標的綜合要求[2]；設計的問題是否兼顧常規問題和非常規問題。因為小學生數學問題解決過程的表現，需要結合數學問題進行測試，而數學問題往往僅局限于定式的考試環節。而這種情況屬于常規問題解決的表現，并不能夠完全囊括小學生數學問題解決全過程的所有表現。在小學數學教學中，同時設置常規數學問題與非常規數學問題，可以培養學生的數學實踐應用能力與探索問題的能力。因此，本研究提出設計問題時要兼顧常規問題與非常規問題，并觀察小學生解決問題時的表現，由此確定小學生思維的活動情況。其次，將小學生的各類表現完整記錄，并通過對不同變量打分，判定學生學習時存在的問題，以便教師提出針對性的改進方案。

（二）整體框架的評價設計

在觀察小學生解決數學問題時的表現后，將所記錄的每一個學生的情況進行匯總，設計評定框架。對學生在框架內的情況賦予相應的分值，明確學生解決問題過程中的表現，并將各類表現進行簡短評價，有效確認評價結果的準確性。如，學生的理解情況可記3分，學生計劃解題的情況可計3分，學生解題的具體步驟可記2分，學生最終的答案可記2分等。在框架內評價小學生解決問題的行為與解決問題的能力，并通過分析學生發現問題、探究問題過程中的具體表現，找到學生存在的問題，進而有針對性地改進教學方案。根據分析，可在整體框架內的評價總結為以下幾點：

1.學生的理解：建立該框架考查學生的理解能力，對于數學問題的認知情況以及學生的不同表現賦值。通過分析分值及學生具體表現，分析學生可能遇到的難題，以便教師給予有效引導，從而促進小學生解決數學問題能力的提升[3]。

2.學生解題的計劃：考查學生對于該類數學問題是否有自己的解題計劃。解題計劃的掌握，對于學生能否快速、準確發現問題有著重要的影響意義。學生按照計劃設定思路，從而進一步確定核心問題，并給予有效判斷。教師在這一過程中，可以通過學生的表述，判定學生解題計劃是否合理，并針對數學問題掌握的情況，給予快速反饋[4]。

3.學生解題的步驟：考查學生是否能夠針對數學問題，提出解題步驟，進一步判定學生的邏輯思維能力狀況。小學生數學問題解決過程的表現，需要結合數學問題進行測試，而數學問題往往僅局限于定式的考試環節。而這種情況屬于常規問題的表現，并不能夠完全反映小學生數學問題解決的情況。對數學常規問題的解決，往往會限定時間。而由于限定時間，往往會讓小學生產生心理負擔，他們表現的解題思維多以程式化的表現居多。因此，在實際教學過程中，觀察小學生解決數學問題的步驟，能夠在一定程度上掌握小學生應用所學知識解決問題能力的狀況。

4.最終答案：學生最終獲得的答案情況。學生通過上述過程，最終會獲得一個結果，這也是驗證學生解題過程是否合理的最重要因素，也是最終檢驗學生數學解題能力的關鍵[5]。學生最終得到的解答結果，與學生的過程表現存在密切相關性。針對解題結果，分析原因，給予有針對性的引導，是分析學生表現的目的之一。

5.綜合性評價：根據學生最終獲得的答案，反思答案正確者數學問題解決過程中的表現情況，明確答案錯誤者在哪一環節出現問題，教師可以重點引導，從而增強教學效果。

綜合上述分析，由此得到評價量表的影響因素，具體如表1所示。

（三）對學生表現的評價方法

1.評價的目的及方法。將本次研究所提觀點進行綜合性評價，進一步證實研究觀點的可行性[6]。將所有數據整理并錄入SPSS24.0分析軟件中，利用大數據分析各量表之間的關系。本研究所選專家均在教育領域工作，并且從事教育工作10年以上，取得中級或以上職稱者，具備客觀判斷事物的能力，能夠保證判斷的準確性[7]。專家人數為10人，使用李克特量表五級評分制方法，對所有研究的數據統計分析，采用1-5分進行標度，分別記為5（非常同意）、4（同意）、3（一般）、2（不同意）、1（非常不同意）。每道題所得數據就是該題態度得分級別，態度在不同級別分值上，可代表調查者態度的強弱[8]。

主要評價指標包括學生的理解、學生解題的計劃、學生解題的步驟、最終答案。

2.統計學方法。將所搜集到的資料經過整理審核后，使用EpiData3.0軟件建立數據庫，采用雙錄入方法錄入。利用SPSS24.0對數據進行描述性統計分析，并采用Pearson相關性分析檢驗。檢驗水準P<0.05，表示有統計學意義。

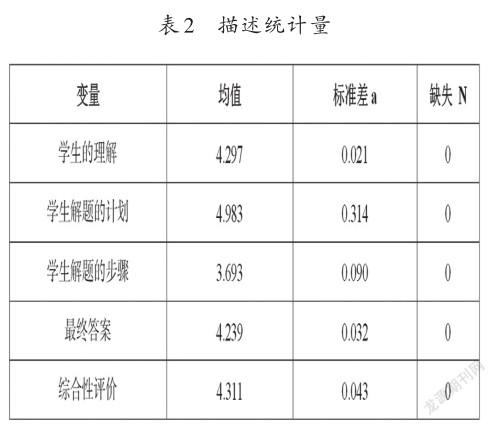
3.評價結果。1）描述統計量。本研究的觀點，大部分專家表示同意，均值最小值為3.693，其余均值在4.0以上。本研究觀點調查結果無缺失，未出現較大偏差，可以進行Pearson相關性分析檢驗。具體描述統計量情況，可見表2所示。

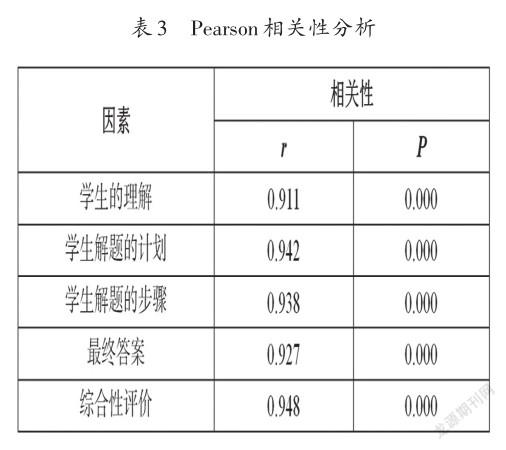
2）Pearson相關性分析。本次研究所提出的觀點，學生的理解、學生解題的計劃、學生解題的步驟、最終答案其r值均在0.90以上，P值均小于0.01，表明本次研究觀點與小學生數學問題解決過程表現的關系具有強相關性。具體結果，見表3所示。

（四）根據分析，總結結果

通過分析學生解決問題的表現，我們發現：學生在解決問題的過程中，存在數學知識應用能力差的問題。究其原因，一是教師設計的問題與生活脫節，完全失去了生活味，二是對學生缺乏有效指導[9]。這要求教師做到兩個“加強”一個“注意”。

兩個“加強”是指：一是加強數學問題與生活實際的聯系。教師要將生活中的數學問題引入課堂，引導學生調用生活經驗分析問題，并嘗試利用所學知識解決問題，以鍛煉學生分析問題和解決問題的能力、數學知識應用能力[10]。如，“反彈數學問題”的思考，上課時出示一些學生熟悉的球類物品，讓學生想象日常生活中球類的使用情況。比如，藍球落地后會反彈，乒乓球也同樣會反彈，從而加深學生對反彈數學問題的理解。

二是加強問題的開放性。開放性問題對培養學生的創新思維具有重要意義，而創新思維是衡量學生解決問題能力的重要因素。因此，在設計問題時，教師一定要注意問題的開放性[11]。筆者認為，教師可以從條件開放、問題開放、解決方法開放三個方面入手。比如，乘車最優化問題就是典型的開放性問題。

一個“注意”是指：注意對學生分析問題、厘清思路的指導[12]。理解題意、厘清思路是問題解決的基礎，教師要引導學生通過畫圖、假設、列表等方式分析問題，提升學生分析問題的能力。比如，乘車最優化問題就可以通過列表的方式進行分析。

綜上所述，分析小學生數學問題解決過程的表現，對教師了解學情，并針對地改進教學方案，進而提升教學效率具有重要意義。這就要求教師要了解學生對知識的理解情況，把握學生解題計劃的制訂，觀察學生解題的步驟，查看最終答案。在此基礎上，合理設定評價框架，判定學生的不足，為正確評價產生解決問題的能力提供翔實數據。

[1]李欣蓮，宋乃慶，陳婷，等.小學數學教師“問題提出”表現研究[J].數學教育學報，2019（02）：05-10.

[2]朱俊華，王乃濤.基于兒童理解的小學數學課堂教學[J].中小學教師培訓，2020（03）：52-55.

[3]曹永勝.小學數學課堂教學有效性的策略研究[J].經濟學，2021（06）：36-37.

[4]葉志強，宋乃慶，陳婷.職前小學教師數學素養認識的質性研究[J].中國電化教育，2019（02）：62-70.

[5]林洪新，楊帥峰，杜雪嬌.小學生數學在線樣例學習的推送策略[J].電化教育研究，2019（11）：121-128.

[6]任偲，蔡丹.執行功能訓練對數學學習困難小學生數學能力的促進作用[J].中國特殊教育，2019（06）：63-71.

[7]方勤華，呂松濤，楊貞貞，等.農村小學數學教師專業發展狀況與學習需求分析——基于《小學教師專業標準》的一次調查[J].數學教育學報，2019（02）：35-40.

[8]李懷軍，張維忠.小學生數學問題提出能力發展研究[J].數學教育學報，2019（05）：02-08.

[9]鄧海英，魏亞楠，嚴卿.小學四年級學生數學情境問題解決能力調查研究——以湖南省為例[J].數學教育學報， 2020（04）：52-57.

[10]宋乃慶，胡睿，蔡金法.用問題提出和問題解決測試小學生對平均數的理解[J].數學教育學報，2020（03）：01-08.

[11]費嶺峰，李桂雙.放大“想”：小學生高階思維培養的重要過程——以“用分數解決問題”教學為例[J].中小學教師培訓，2020（09）：04.

[12]趙倩，呂世虎，韓繼偉.中國大陸與臺灣地區小學生數感表現的比較研究——以比較分數的相對大小為例[J].數學教育學報，2019（06）：65-70.

編輯：謝穎麗