一類二次可逆Lotka-Volterra系統(tǒng)的全局相圖

邵 儀，吳澤敏，李文仙

（肇慶學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，廣東 肇慶 526061）

1 預(yù)備定理

自上世紀(jì)以來，為解決Hilbert十六問題，平面多項(xiàng)式系統(tǒng)一直是常微分方定性理論和分支理論研究的熱點(diǎn)，尤其是平面多項(xiàng)式系統(tǒng)的極限環(huán)個(gè)數(shù)問題，更是分支問題研究的重中之重.研究二次系統(tǒng)的擾動(dòng)系統(tǒng)最多有多少個(gè)極限環(huán)一直是許多學(xué)者研究的熱點(diǎn)問題之一[1-2].利用常微分方定性理論，研究系統(tǒng)在有限平面和無限遠(yuǎn)平面奇點(diǎn)的性質(zhì)、極限環(huán)的存在性與位置，以及過奇點(diǎn)的分界線的去向等，得到系統(tǒng)的全局相圖.通過全局相圖我們可以直觀了解系統(tǒng)的軌線走向和動(dòng)力學(xué)性態(tài)，從而為進(jìn)一步研究擾動(dòng)系統(tǒng)的分支等問題提供必要的研究準(zhǔn)備.COLAK I E等[3]研究了具有冪零中心的三次齊次哈密爾頓系統(tǒng)的全局相圖.TIAN Y等[4]研究了關(guān)于y軸對(duì)稱的四次齊次哈密爾頓系統(tǒng)的全局相圖和分支圖.但對(duì)于二次系統(tǒng)到底能有多少種拓?fù)浣Y(jié)構(gòu)互不相同的相圖，至今依然是個(gè)沒有完全解決的問題，需要不斷的補(bǔ)充和完善.

本文將研究一類二次可逆Lotka-Volterra系統(tǒng)[1]

的全局相圖，其中b為參數(shù).利用常微分定性理論，我們將證明這是一類沒有極限環(huán)的二次系統(tǒng).首先我們研究系統(tǒng)在有限平面奇點(diǎn)的拓?fù)浞诸悾缓笱芯克跓o窮遠(yuǎn)點(diǎn)的拓?fù)浣Y(jié)構(gòu)，最后在Poincaré緊化盤中得到系統(tǒng)（1.1）有6類不同的拓?fù)涞葍r(jià)相圖.

令z=x+iy，則系統(tǒng)（1.1）可化為：

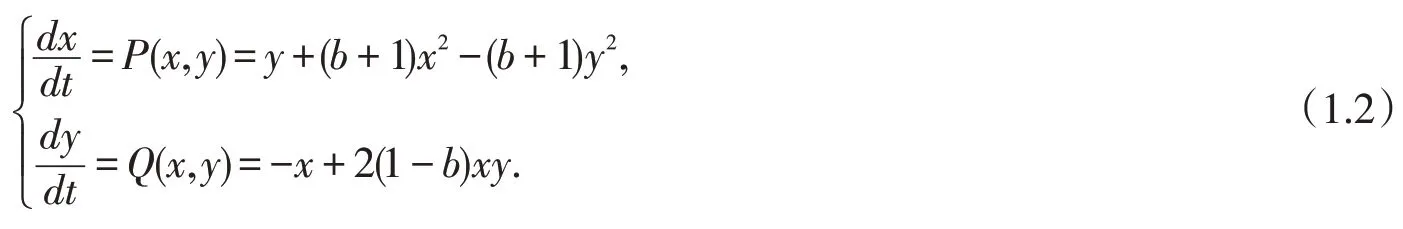
設(shè)系統(tǒng)（1.2）的線性近似方程為

若(xo,yo)是系統(tǒng)（1.2）的奇點(diǎn)，則線性近似方程（1.3）的系數(shù)矩陣為

為了研究系統(tǒng)（1.2）的拓?fù)淙窒鄨D，我們給出下面幾個(gè)預(yù)備定理.

定理1[5]：如果線性近似方程（1.3）系數(shù)矩陣A的特征根實(shí)部非零，且不是重根，那么非線性方程（1.2）在平衡點(diǎn)(xo,yo)附近的軌線與它的線性近似方程（1.3）在原點(diǎn)附近的軌線拓?fù)浣Y(jié)構(gòu)相同，為穩(wěn)定的焦點(diǎn)或者結(jié)點(diǎn)、不穩(wěn)定的焦點(diǎn)或結(jié)點(diǎn)、或鞍點(diǎn).

定理2[6]：（對(duì)稱原理）若原點(diǎn)O是系統(tǒng)（1.3）的中心，且系統(tǒng)（1.2）滿足條件

P(x,-y)=-P(x,y),Q(x,-y)=Q(x,y)或P(-x,y)=P(x,y),Q(-x,y)=-Q(x,y),則原點(diǎn)O也是系統(tǒng)（1.2）的中心.

定理3[7]：具有中心的二次系統(tǒng)不存在極限環(huán).

通過研究系統(tǒng)（1.2）在有限平面和無窮遠(yuǎn)奇點(diǎn)的各種類型，我們得到本文主要結(jié)論為以下定理：

定理：系統(tǒng)（1.2）的全局相圖，有6種不同的拓?fù)浣Y(jié)構(gòu).見圖1至圖6.

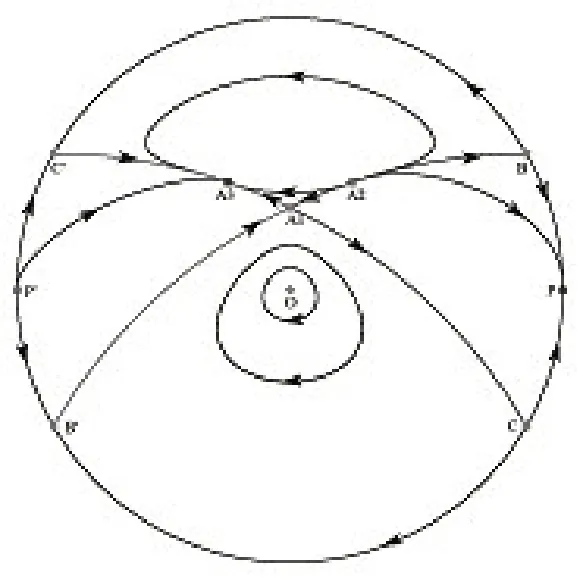
圖1

（2）當(dāng)b＞1（或b＜-1）時(shí)，在有限平面上有一個(gè)中心，三個(gè)鞍點(diǎn).在右（或左）半平面y＞0（或y＜0）的無窮遠(yuǎn)處有一個(gè)穩(wěn)定結(jié)點(diǎn)，兩個(gè)不穩(wěn)定結(jié)點(diǎn)，對(duì)應(yīng)在左半平面y＜0（或y＞0）的無窮遠(yuǎn)處有一個(gè)不穩(wěn)定結(jié)點(diǎn)，兩個(gè)穩(wěn)定結(jié)點(diǎn)，相圖見圖2；

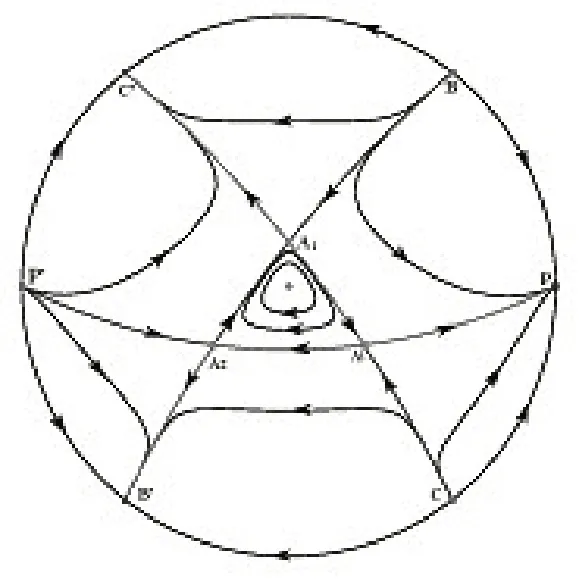
圖2 b ＞1

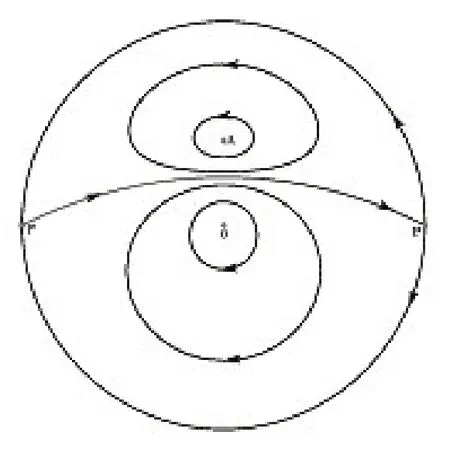
圖3

（4）當(dāng)b=1時(shí)，在有限平面上有一個(gè)中心，一個(gè)鞍點(diǎn).在右半平面y＞0 的無窮遠(yuǎn)處有一個(gè)穩(wěn)定結(jié)點(diǎn)，兩個(gè)半雙曲奇點(diǎn)為鞍結(jié)點(diǎn)，在左半平面y＜0 的無窮遠(yuǎn)處對(duì)應(yīng)一個(gè)不穩(wěn)定結(jié)點(diǎn)，兩個(gè)鞍結(jié)點(diǎn)，相圖見圖4；

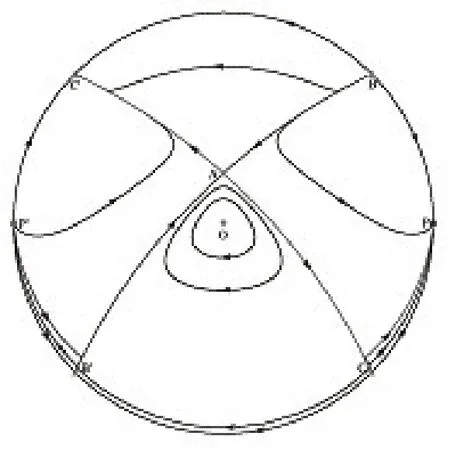
圖4 b=1

（5）當(dāng)b=-1時(shí)，在有限平面上只有一個(gè)中心.在右半平面y＞0 的無窮遠(yuǎn)處有一個(gè)半雙曲鞍點(diǎn)，在左半平面y＜0 的無窮遠(yuǎn)處對(duì)應(yīng)一個(gè)半雙曲鞍點(diǎn)，在y軸正半軸的無窮遠(yuǎn)處有一個(gè)冪零奇點(diǎn)，在y軸負(fù)半軸的無窮遠(yuǎn)處對(duì)應(yīng)有一個(gè)冪零奇點(diǎn)，相圖見圖5；

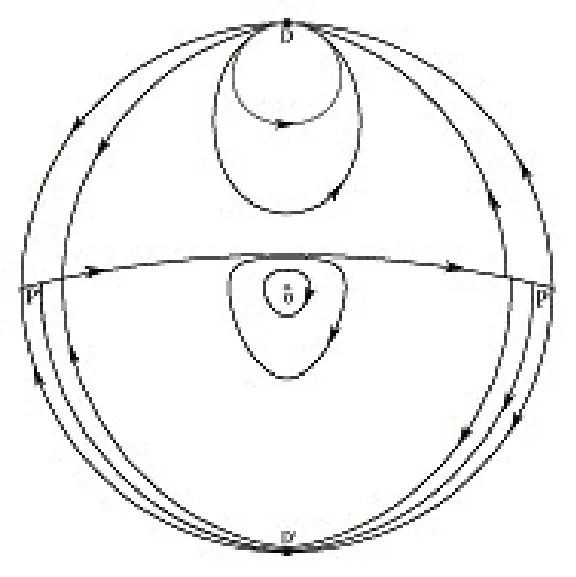
圖5 b=-1

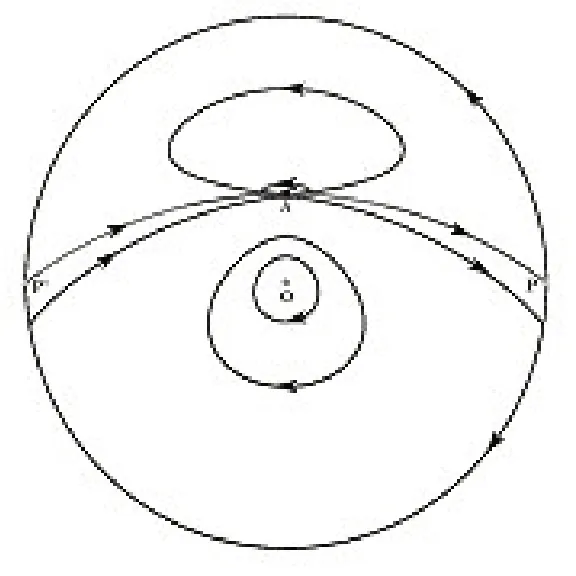
圖6 b=1/3

2 有限平面奇點(diǎn)及性態(tài)

這部分我們主要研究系統(tǒng)（1.2）在有限平面的奇點(diǎn)類型、穩(wěn)定性以及它們附近的軌線性態(tài)，為此我們有下面的引理.

引理1：在有限平面，系統(tǒng)（1.2）的奇點(diǎn)類型及性態(tài)如下：

（2）當(dāng)b＞1（或b＜-1）時(shí)，系統(tǒng)也有四個(gè)奇點(diǎn)，分別是中心O(0,0)，鞍點(diǎn)

（4）當(dāng)b=1時(shí)，有兩個(gè)奇點(diǎn)，分別是中心O(0,0)和鞍點(diǎn)

（5）當(dāng)b=-1時(shí)，僅有一個(gè)奇點(diǎn)O(0,0)是中心；

證明：應(yīng)用常微分方程定性理論，設(shè)系統(tǒng)（1.2）的奇點(diǎn)為(xo,yo)，則系統(tǒng)（1.2）在(xo,yo)處的線性近似方程（1.3）的系數(shù)矩陣為

令系統(tǒng)（1.2）中的P(x,y=Q(x,y)=0,容易得到當(dāng)＜b＜1，或b＞1，或b＜-1 時(shí)，系統(tǒng)（1.2）有四個(gè)奇點(diǎn)和；當(dāng)時(shí)，系統(tǒng)(1.2)有兩個(gè)奇點(diǎn)O(0,0)和；當(dāng)b=1 時(shí)，有兩個(gè)奇點(diǎn)O(0,0)和；當(dāng)b=-1 時(shí)，系統(tǒng)(1.2)僅有一個(gè)奇點(diǎn)O(0,0)；當(dāng)時(shí)，有兩個(gè)奇點(diǎn)中心O(0,0)和.

對(duì)于奇點(diǎn)O，易知b取任意實(shí)數(shù)，O都是系統(tǒng)（1.3）的奇點(diǎn)，系數(shù)矩陣（2.1）的特征值為i和-i，所以O(shè)是此線性近似方程（1.3）的中心.又因?yàn)橄到y(tǒng)（1.2）滿足P(-x,y)=P(x,y),Q(-x,y)=-Q(x,y)，所以由對(duì)稱原理定理2可知，原點(diǎn)O也是系統(tǒng)（1.2）的中心.下面我們分情況討論除O(0,0)外其他奇點(diǎn)的情形.

（2）當(dāng)b＞1或b＜-1時(shí)，易求得奇點(diǎn)A1，A2和A3的特征值與（i）的相等，但由于的取值范圍不同，所以三個(gè)奇點(diǎn)對(duì)應(yīng)系數(shù)矩陣（2.4）的特征值均為異號(hào)實(shí)根，故奇點(diǎn)A1，A2和A3都是系統(tǒng)（1.2）的鞍點(diǎn).

令ξ=x,η=則有

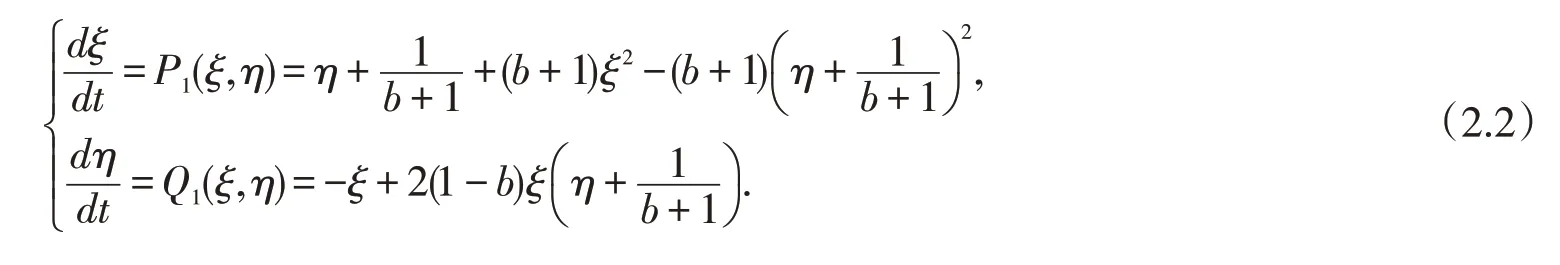
因?yàn)?/p>

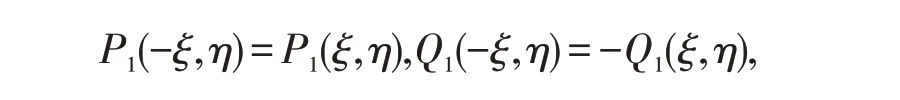
由對(duì)稱原理可知，原點(diǎn)是系統(tǒng)（2.2）的中心，故A也是原系統(tǒng)（1.2）的中心.

（4）當(dāng)b=1 時(shí)，易求得奇點(diǎn)對(duì)應(yīng)的系數(shù)矩陣（2.1）的特征值為λ=-+1，故A是原系統(tǒng)（1.2）的鞍點(diǎn).

（5）當(dāng)b=-1情形，只有一個(gè)中心奇點(diǎn)O(0,0)，上述已證.

系統(tǒng)（1.2）化為系統(tǒng)

由y+P2(x,y)=0 解得隱函數(shù)

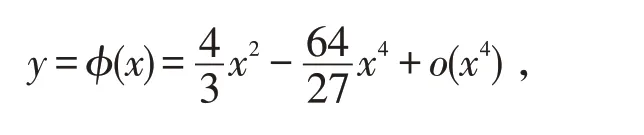
并且

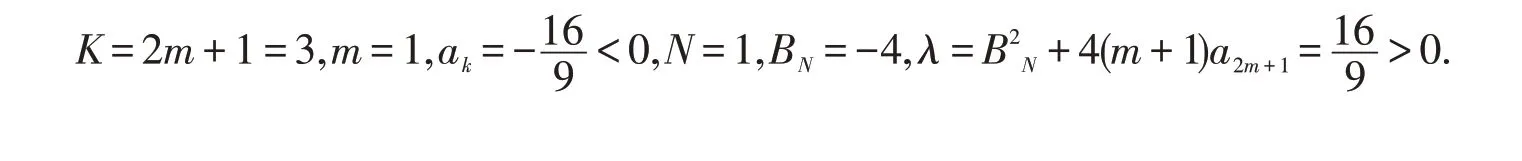
由文獻(xiàn)[8]的定理7.2及坐標(biāo)變換(2.3)可知，奇點(diǎn)的鄰域由一個(gè)橢圓扇形與一個(gè)雙曲扇形組成，并且橢圓扇形在雙曲扇形的上方.

這樣我們就完成了系統(tǒng)（1.2）在有限平面上所有奇點(diǎn)性態(tài)的分析.

引理2：系統(tǒng)（1.2）是沒有極限環(huán)的系統(tǒng).

證明：由引理1的證明知道，不論b取何值，系統(tǒng)（1.2）都有一個(gè)奇點(diǎn)是中心O，由定理3，系統(tǒng)（1.2）沒有極限環(huán).

3 無限遠(yuǎn)奇點(diǎn)及性態(tài)

這部分我們將通過運(yùn)用Poincaré變換，研究系統(tǒng)（1.2）在無窮遠(yuǎn)處的奇點(diǎn)類型以及軌線性態(tài)，為此我們有如下引理.

引理3：在無限遠(yuǎn)處，系統(tǒng)（1.2）的奇點(diǎn)性態(tài)為

（2）當(dāng)b＞1（或b＜-1）時(shí)，系統(tǒng)（1.2）有三個(gè)奇點(diǎn)，分別是穩(wěn)定（或不穩(wěn)定）結(jié)點(diǎn)P(0,0)，不穩(wěn)定（或穩(wěn)定）結(jié)點(diǎn)

（4）當(dāng)b=1 時(shí)，系統(tǒng)有三個(gè)奇點(diǎn)，分別是穩(wěn)定非正常結(jié)點(diǎn)P(0,0)，半雙曲的鞍結(jié)點(diǎn)B(1,0)和C(-1,0)，B點(diǎn)和C點(diǎn)鄰域的軌線由一個(gè)拋物扇形與兩個(gè)雙曲扇形組成，B點(diǎn)的拋物扇形在Poincaré圓盤內(nèi)，而C點(diǎn)的兩個(gè)雙曲扇形在Poincaré圓盤內(nèi)；

（5）當(dāng)b=-1時(shí)，系統(tǒng)（1.2）有兩個(gè)奇點(diǎn)，分別是半雙曲鞍點(diǎn)P(0,0)以及y軸正半軸上的冪零奇點(diǎn)D(0,0)，D的鄰域的軌線由一個(gè)橢圓扇形與一個(gè)雙曲扇形組成，且橢圓扇形在圓盤內(nèi)，而對(duì)應(yīng)y軸負(fù)半軸上的橢圓扇形不在圓盤內(nèi).

證明：我們先求系統(tǒng)（1.2）在x-y平面除y軸上的兩個(gè)無窮遠(yuǎn)點(diǎn)以外的無窮遠(yuǎn)點(diǎn)的情況.為此作Poincaré變換，令，即，將系統(tǒng)（1.2）化為u-z平面上的方程組

令z=0，系統(tǒng)（3.1）在u軸上的奇點(diǎn)，即滿足(1-3b)u+(b+1)u3=0.容易解出當(dāng)和b＜-1時(shí)，系統(tǒng)（3.1）在u軸上有三個(gè)奇點(diǎn)；當(dāng)時(shí)，系統(tǒng)（3.1）在u軸上只有一個(gè)奇點(diǎn)P(0,0)；當(dāng)b=1時(shí)，系統(tǒng)（3.1）在u軸上有三個(gè)奇點(diǎn)P(0,0)，B(1,0)和C(-1,0).

易求得系統(tǒng)（3.1）的線性近似方程組的系數(shù)矩陣為

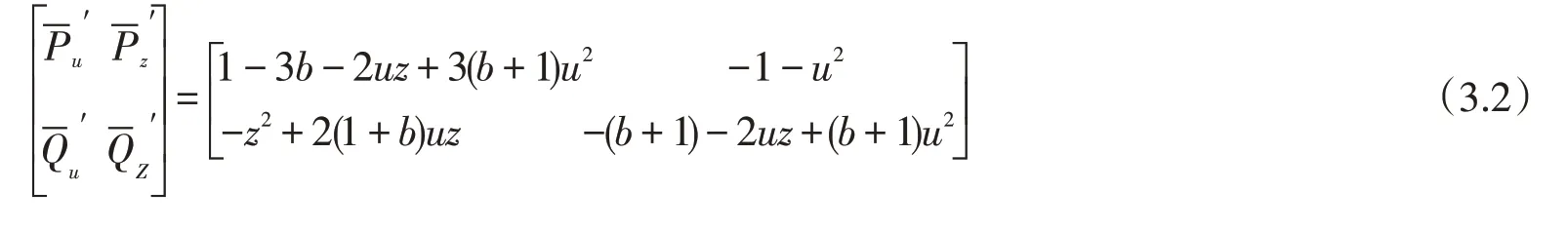
（2）當(dāng)b＞1 或b＜-1 時(shí)，奇點(diǎn)P,B,C的特征值與情形（i）相等.容易看出當(dāng)b＞1 時(shí)，P點(diǎn)的兩個(gè)特征值為相異的負(fù)實(shí)根，B點(diǎn)和C點(diǎn)的兩個(gè)特征值為相異的正實(shí)根，而當(dāng)b＜-1 時(shí)，奇點(diǎn)P,B,C的特征值與b＞1 的特征值符號(hào)正好相反.因此當(dāng)b＞1 時(shí)，P是穩(wěn)定結(jié)點(diǎn)、B點(diǎn)和C點(diǎn)均為不穩(wěn)定結(jié)點(diǎn)；當(dāng)b＜-1 時(shí)，P是不穩(wěn)定結(jié)點(diǎn)、B點(diǎn)和C點(diǎn)均為穩(wěn)定結(jié)點(diǎn).

（4）當(dāng)b=1 時(shí)，易求得P(0,0)的兩個(gè)特征值相等是-2，因此P是穩(wěn)定非正常結(jié)點(diǎn).而B點(diǎn)和C點(diǎn)的特征值為4 和0，屬于高階奇點(diǎn)，這種情形較為復(fù)雜.我們先討論B點(diǎn)的情形.為此我們先做坐標(biāo)變換u→u-1,z→z，將B點(diǎn)平移到u-z平面的原點(diǎn)，方程組（3.1）變?yōu)?/p>

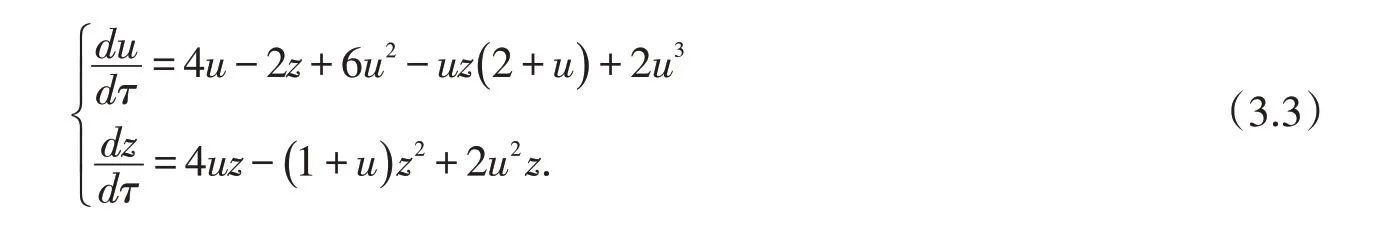
為了確定高階奇點(diǎn)B的類型，我們?cè)僮鲎鴺?biāo)變換

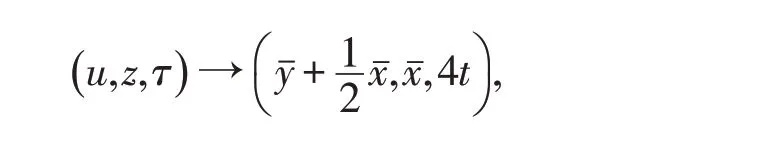
將方程組（3.3）化為

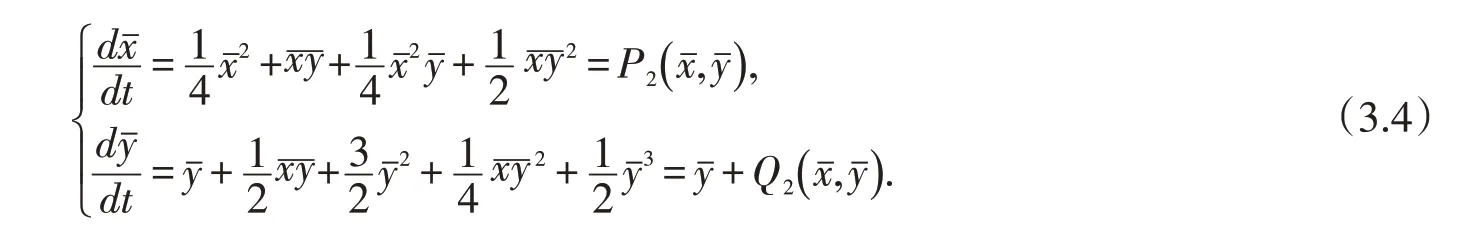
應(yīng)用文獻(xiàn)[8]的定理7.1，系統(tǒng)在奇點(diǎn)O(0,0)的充分小鄰域內(nèi)，解析函數(shù)?(xˉ)=0 滿足?(xˉ)+Q2(xˉ,?(xˉ))≡0.令，所以O(shè)(0,0)是鞍結(jié)點(diǎn)，O點(diǎn)鄰域的軌線由分別沿著y正半軸和負(fù)半軸進(jìn)入O點(diǎn)的兩條分界線分成兩部分，一部分是拋物扇形，一部分是兩個(gè)雙曲扇形，而且拋物扇形在xˉ-yˉ平面的右半平面.方程組（3.4）與（3.1）是拓?fù)涞葍r(jià)的，故高階奇點(diǎn)B也是鞍結(jié)點(diǎn)，其鄰域的軌線拓?fù)涞葍r(jià)于O點(diǎn)鄰域的軌線性態(tài).由坐標(biāo)變換可知，xˉ-yˉ平面的右半平面對(duì)應(yīng)方程組（3.1）z＞0，故拋物扇形在Poincaré圓盤內(nèi).

高階奇點(diǎn)C的情形與B點(diǎn)討論類似，我們直接做坐標(biāo)變換

方程組（3.1）變?yōu)?/p>

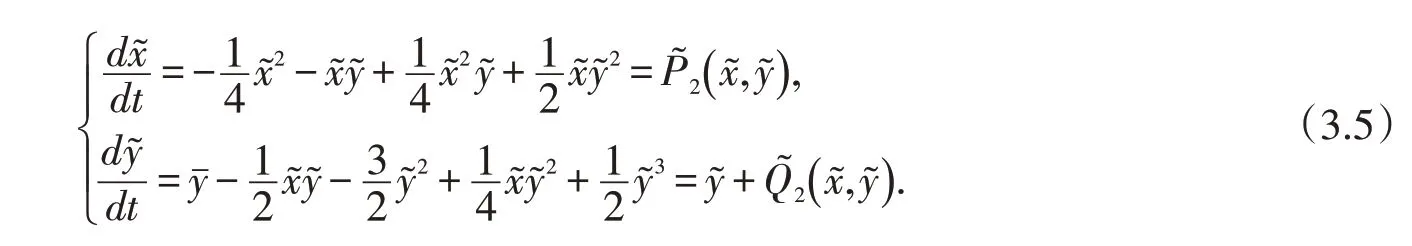
同時(shí)將C點(diǎn)平移到了原點(diǎn).同樣應(yīng)用文獻(xiàn)[8]的定理7.1，解析函數(shù)滿足≡0，，即，即O(0,0)也是鞍結(jié)點(diǎn)，O點(diǎn)鄰域的軌線分成兩部分，一部分是拋物扇形，一部分是兩個(gè)雙曲扇形，而且兩個(gè)雙曲扇形在?平面的右半平面.由于方程組（3.5）與（3.1）也是拓?fù)涞葍r(jià)的，故高階奇點(diǎn)C也是鞍結(jié)點(diǎn)，即為半雙曲奇點(diǎn)，其鄰域的軌線拓?fù)涞葍r(jià)于O點(diǎn)鄰域的軌線性態(tài).由上述坐標(biāo)變換可知，?平面的右半平面對(duì)應(yīng)方程組（3.1）z＞0,故兩個(gè)雙曲扇形在Poincaré圓盤內(nèi).

（5）當(dāng)b=-1 時(shí)，易求得P(0,0)的兩個(gè)特征值為4 和0，也屬于高階奇點(diǎn).與（4）中B點(diǎn)的討論情形類似，不難求得坐標(biāo)變換

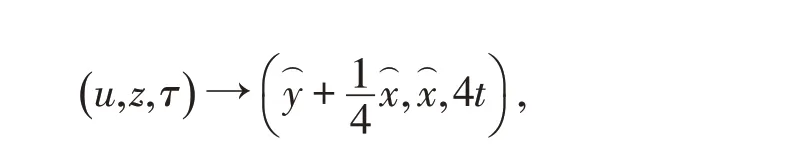
將方程組（3.1）變?yōu)橐韵路匠探M

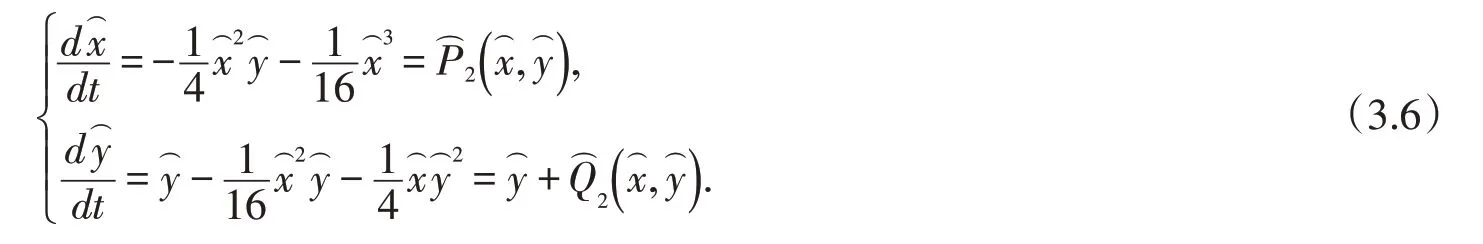
應(yīng)用文獻(xiàn)[8]的定理7.1，方程組（3.6）在P(0,0)的小鄰域內(nèi)存在解析函數(shù)滿足令，即，所以P(0,0)是半雙曲鞍點(diǎn).

將方程組（3.1）變?yōu)榉匠探M

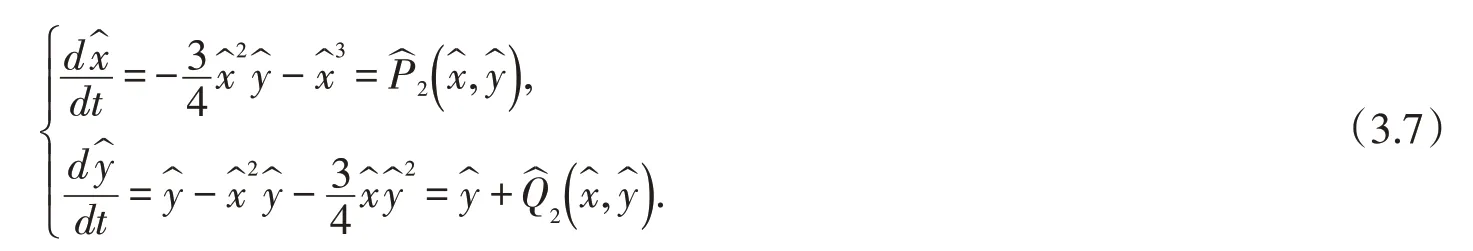
由文獻(xiàn)[8]的定理7.1，方程組（3.7）在P(0,0)的小鄰域內(nèi)，解析函數(shù)=0 滿足?(x)+Q2(x,?(x))≡0.令，即m=3,am=-1 ＜0，所以P(0,0)是半雙曲鞍點(diǎn).

接下來研究y軸上的兩個(gè)無窮遠(yuǎn)點(diǎn).運(yùn)用Poincaré變換,即，將系統(tǒng)（1.2）變換為ν-z平面上的方程組：

只要研究方程組（3.8）在點(diǎn)(v,z)=(0,0)附近的情況，就可以確定系統(tǒng)（1.2）在x-y平面上y軸方向的兩個(gè)無窮遠(yuǎn)點(diǎn)的情況.

當(dāng)方程組（3.8）滿足(v,z)=(0,0)時(shí)，只有b=-1，這時(shí)方程組（3.8）簡(jiǎn)化為

方程組（3.9）的線性近似方程組的系數(shù)矩陣為

容易求得奇點(diǎn)D(0,0)處的兩個(gè)特征值均為0.應(yīng)用文獻(xiàn)[8]的定理7.2，容易求得方程組（3.9）存在隱函數(shù)z=?(ν)=4ν2+4ν4+O(ν6)滿足z+P(ν,z)=0，并有

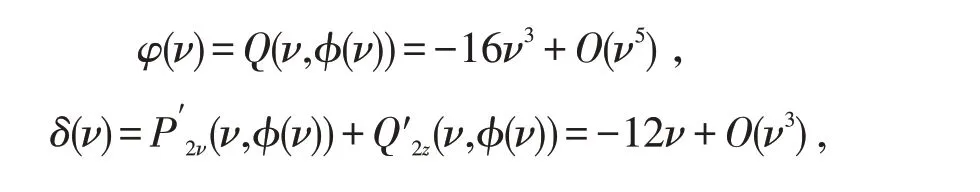
即

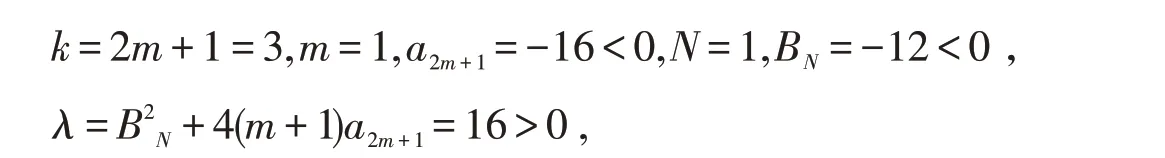
故D(0,0)的鄰域軌線由一個(gè)橢圓扇形和一個(gè)雙曲扇形組成，且在ν-z平面中，橢圓扇形在雙曲扇形的上方.由于z＞0 對(duì)應(yīng)Poincaré圓盤y＞0 在圓內(nèi)部分，因此橢圓扇形在圓盤內(nèi).至此，我們完成了引理3的證明.

定理的證明：結(jié)合引理1和引理3，我們就證明了二次可逆Lotka-Volterra 系統(tǒng)z?=-iz+z2+bzˉ2在有限平面和無窮遠(yuǎn)處的奇點(diǎn)類型及軌線性態(tài).綜合分析就可以畫出二次可逆Lotka-Volterra 系統(tǒng)z?= -iz+z2+bzˉ2當(dāng)參數(shù)b各種取值范圍的全局相圖.需要注意的是b＞1 和b＜-1 的全局相圖是拓?fù)涞葍r(jià)的，我們只需要運(yùn)用坐標(biāo)變換(x,y,t)→(-x,-y,t)，一種情形的相圖就拓?fù)涞葍r(jià)于另一種情形的相圖.

4 結(jié)語(yǔ)

通過利用微分方程定性理論，對(duì)一類二次可逆Lotka-Volterra 系統(tǒng)在有限平面及無窮遠(yuǎn)平面的初等奇點(diǎn)、半雙曲奇點(diǎn)以及冪零奇點(diǎn)進(jìn)行了研究，得到了6類拓?fù)涞葍r(jià)的全局相圖.