扭王字塊體斜坡堤越浪量的數值研究

2022-04-02 05:56:18孫大鵬孫文豪修富義

海洋工程 2022年2期

孫大鵬，孫文豪，修富義，劉飛

(1.大連理工大學海岸與近海工程國家重點實驗室，遼寧大連 116024；2.水發規劃設計有限公司，山東臨沂 276037；3.沈陽吉天置業有限公司，遼寧沈陽 110165；4.長春中海地產有限公司，吉林長春 130117)

由于數值模擬的研究方法相比物模試驗具有很多優勢，對于斜坡堤越浪量的數值研究，許多學者進行了大量探索。Losada等[1]和Guanche等[2]基于COBRAS-UC模型，開展了海堤波浪的數值模擬和計算，通過和試驗值比較來證明模型的有效和準確。曾冬[3]使用DualSPHysics模型模擬了規則和不規則波入射時斜坡堤的越浪。王鵬等[4]采用了線性波理論，二次開發FLUENT軟件并實現了質量源造波，通過建立多孔介質模型數值模擬了塊體護面斜坡堤的越浪。王鍵等[5]在FLUENT軟件中開發了二維不規則波的波浪水槽，模擬了單波的斜坡堤越浪量。李東洋等[6]基于OpenFOAM軟件進行三維數值水槽中水體在斜坡堤內流動情況的研究。修富義[7]結合物模試驗開展了基于FLUENT軟件的二維扭王字塊體護面斜坡堤越浪量的數值模擬，模型中引入了系數C，并給出了坡度系數m=1.5的系數C的計算關系式。

鑒于《港口與航道水文規范》(JTS145—2015)[8]缺少扭王字塊體斜坡堤越浪量的計算關系式，且目前有關扭王字塊體斜坡堤越浪量的數值研究很少，雖然修富義[7]給出了考慮因素相對全面的研究成果，但所給C值的計算關系式僅適用于m=1.5的情況。基于修富義[7]的數值構想，并結合前期的物理模型試驗[9]，繼續進行m=2.0、2.5的扭王字塊體斜坡堤越浪量數值模擬研究，并且分別給出系數C的計算關系式，以方便供實際工程應用。

1 數值水槽的建立與模擬工況

1.1 控制方程

采用二維黏性流體的連續性方程、動量方程作為基本控制方程，采用RNG k-ε模型模擬湍流效應，流體自由表面的捕捉采用流體體積(VOF)方法。基本控制方程為：

(1)

(2)

(3)

式中：ρ為流體密度；u和w分別為x和z方向的速度；μ為黏性系數；p為壓強；Fx和Fy分別為附加源項。

1.2 數值水槽的概況

采用唐蔚等[10]與王鍵等[11]構建的數值波浪水槽，造波方式為主動吸收式造波，其原理為：在造波邊界前部安放兩個浪高儀用于采集波浪數據，將數據通過濾波變換得到造波修正信號，根據修正信號在造波端會產生額外速度來吸收掉反射波，達到消除二次反射的目的。水槽的具體尺寸和裝置設置見圖1。

圖1 數值波浪水槽

1.3 數值水槽的驗證

不規則波的波浪譜選用Jonswap譜，用于數值水槽驗證的波浪參數為：Hs=0.112 6 m(有效波高)，Tp=1.55 s(譜峰周期)，d=0.45 m(水深)。選取距離造波板15.0 m及19.0 m處的兩個位置對波浪數據進行監測及收集，處理收集波浪數據后繪制出模擬波浪譜，通過與目標波浪靶譜的對比，從而鑒定文中采用的數值水槽所造波浪的準確性。波浪參數的統計值如表1所示，模擬波浪譜與目標靶譜的對比見圖2。

表1 波浪參數

圖2 模擬譜與目標靶譜

1.4 數值模擬的工況

文中斜坡堤越浪數值模擬的試驗工況采用與前期物模試驗[9]相同的工況，見表2。為使所產生波浪的個數大于100個，數值造波時長為180 s。在FLUENT軟件中，將斜坡堤模型上鋪設扭王字塊體的區域設置為多孔介質區，并采用多孔介質中的系數C來表示塊體在斜坡堤模型上的消波作用。

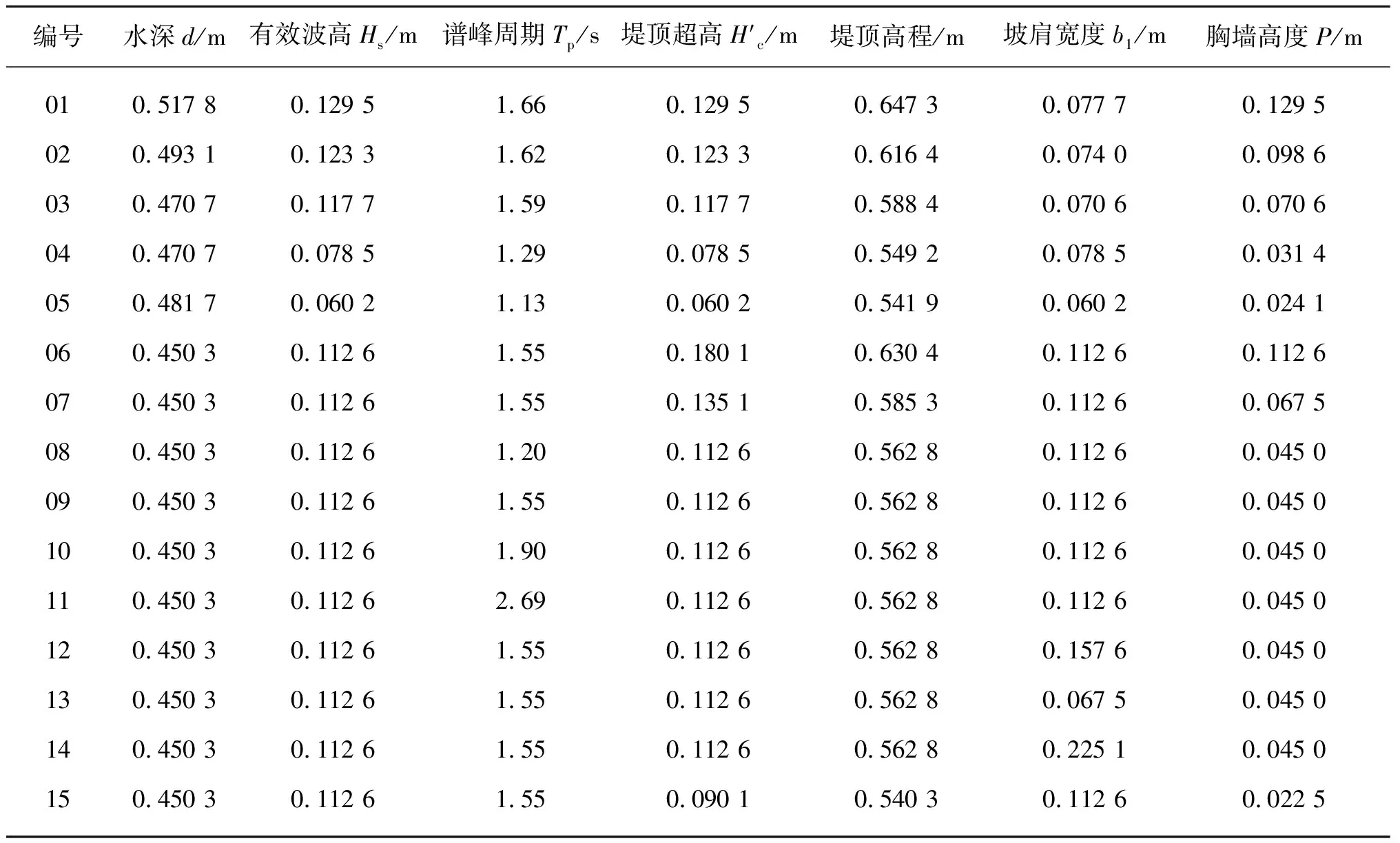
表2 數值試驗工況

斜坡堤模型的邊界設置為固壁邊界，不具有滲透性；斜坡堤模型上鋪設的塊體采用滿足穩定性要求的3種扭王字塊體(h=0.042 m、0.060 m、0.078 m)，扭王字塊體尺寸[12]如圖3所示。

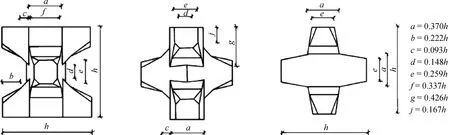
圖3 扭王字塊尺寸示例

2 系數C的率定方法

以坡度m=2.0、塊體尺寸h=0.042 m、表2中編號為01的試驗工況為例來說明系數C的率定方法：第一步，假定一組C值(文中取0.1、0.5、1.0、2.0、5.0)，分別輸入FLUENT軟件中可數值計算出每個假定的C值對應的越浪量值；第二步，采用上一步得出的數值計算結果繪制出一條01試驗工況的越浪量與C值之間的關系曲線，如圖4(編號01)所示；第三步，采用01試驗工況的物模試驗[9]越浪量值從曲線(編號01)上反查得到01試驗工況系數的率定值C率定。重復上述率定方法步驟，圖4給出了m=2.0、h=0.042 m的15種工況越浪量與C之間關系曲線的率定結果。表3、表4分別為m=2.0、2.5的3種尺寸扭王字塊體系數C的率定值。

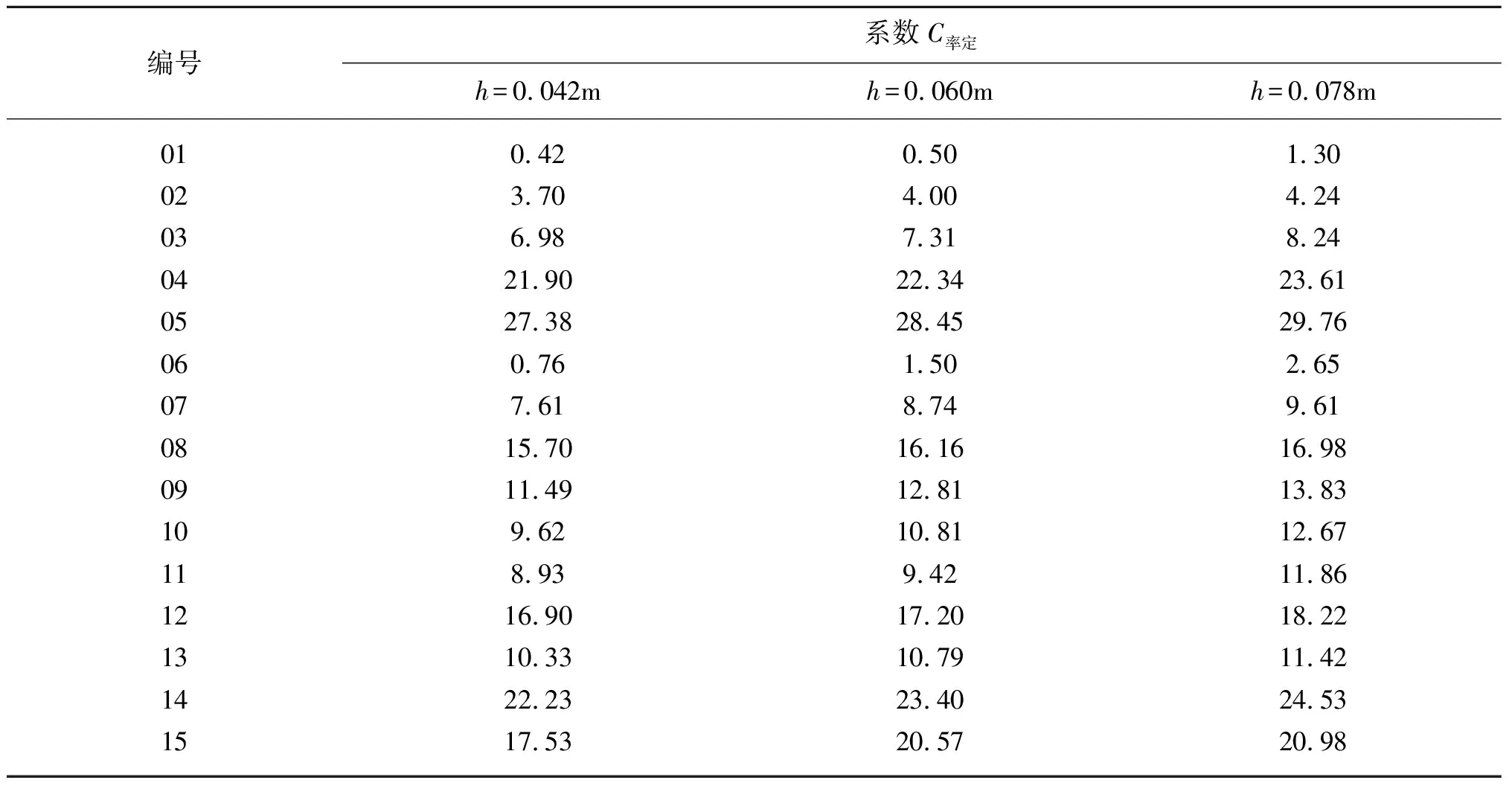
表4 m=2.5的C率定值

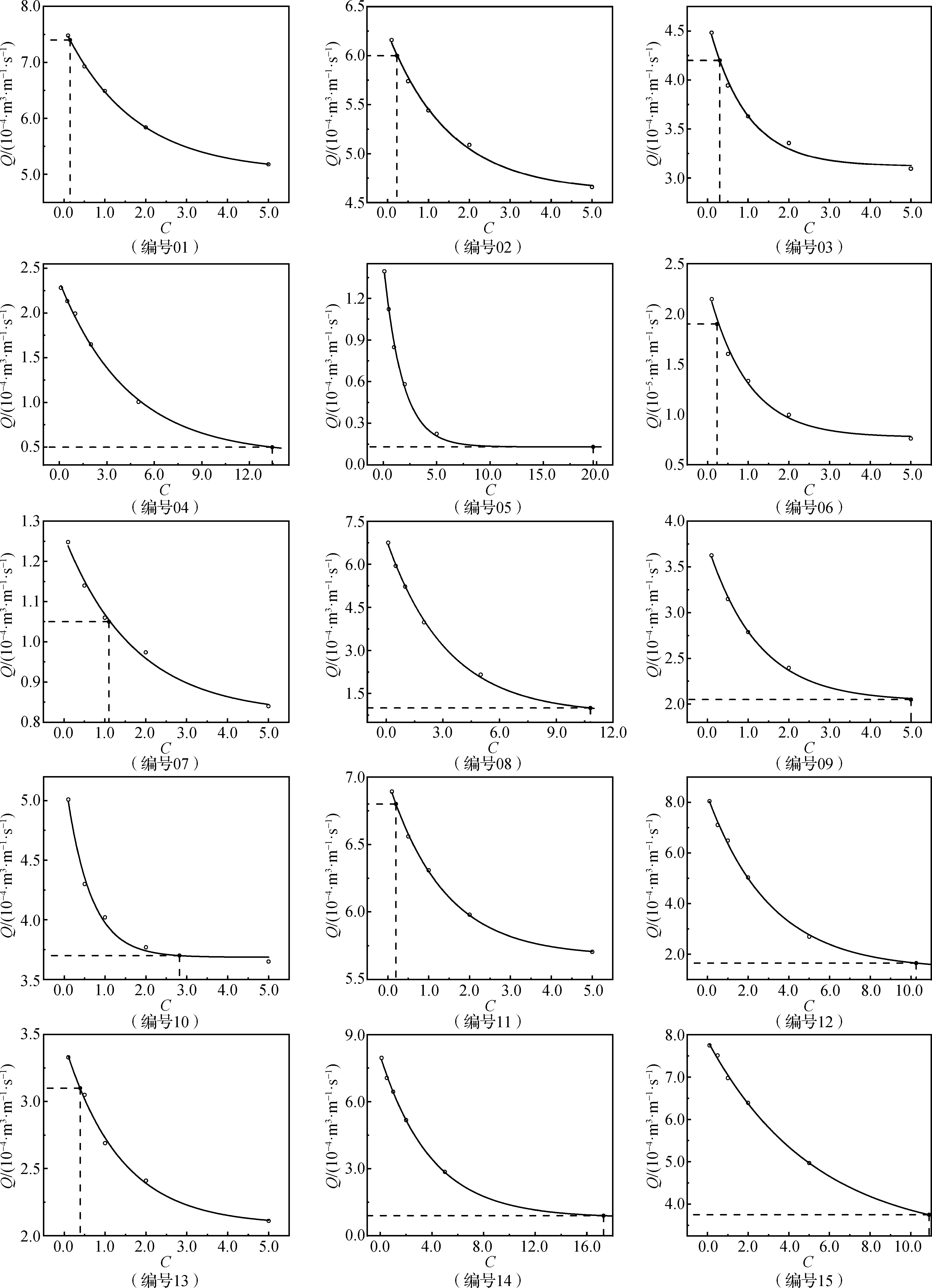
圖4 m=2.0、h=0.042 m的C值曲線

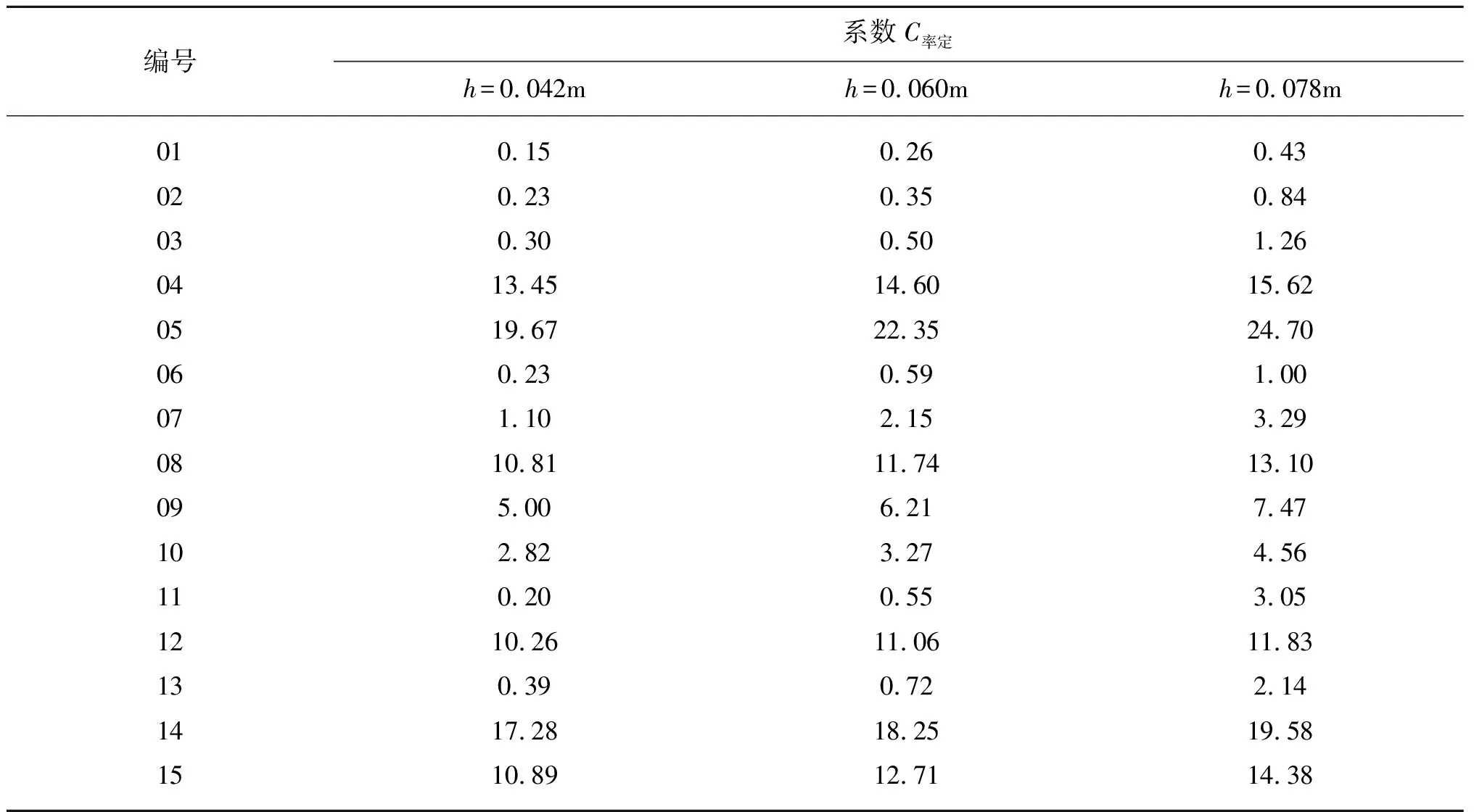
表3 m=2.0的C率定值

為了驗證C率定值的準確性，再將C率定值輸入FLUENT軟件中進行數值計算，并把數值計算所得越浪量值與物模試驗[9]越浪量值進行對比，如圖5所示。圖5中可知，數模值與試驗值[9]吻合較好，表明文中給出的C率定值較為準確。

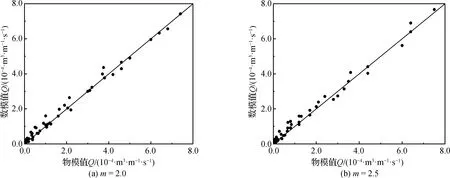
圖5 物模值Q與數模值Q

3 系數C計算關系式

修富義[7]曾給出坡度系數m=1.5的系數C，其計算關系式為：

(4)

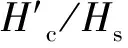
基于文中數模成果的分析可知：越浪量對C值比較敏感；不同坡度系數m對應的C值與各影響因素之間的函數關系差異較大。為確保數值模擬成果有較高的計算精度，可供實際工程的設計應用，這里延續修富義[7]的數值模擬思路及分析方法，在相同工況下，將分別給出坡度系數m=2.0、2.5的C值計算關系式。

基于π定理，得出C值的無因次計算關系式為：

(5)

3.1 坡度系數m=2.0的C值計算關系式

3.1.1C隨Hs/L的變化趨勢

僅改變Hs/L的取值，圖6給出了C值隨波陡變化的趨勢。在圖6所示范圍內，Hs/L增大時C也逐漸增大，呈線性函數關系。

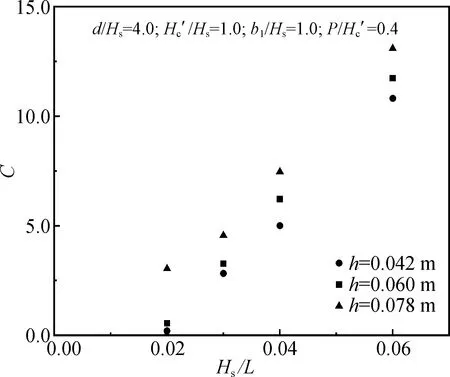
圖6 C隨Hs/L的變化趨勢

3.1.2C隨d/Hs的變化趨勢

僅改變d/Hs的取值，圖7給出了C值隨相對水深變化的趨勢。在圖7所示范圍內，d/Hs增大時C也逐漸增大，呈對數函數關系。

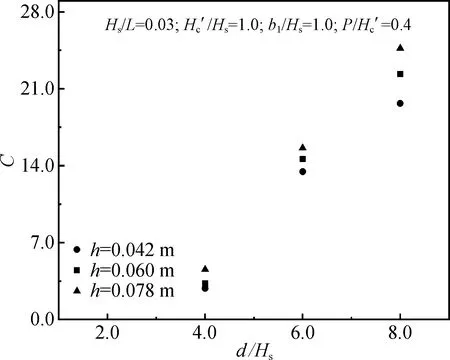
圖7 C隨d/Hs的變化趨勢

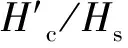
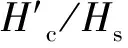
圖8 C隨的變化趨勢

3.1.4C隨b1/Hs的變化趨勢

僅改變b1/Hs的取值，圖9給出了C值隨相對坡肩寬度變化的趨勢。在圖9所示范圍內兩者呈線性函數關系。

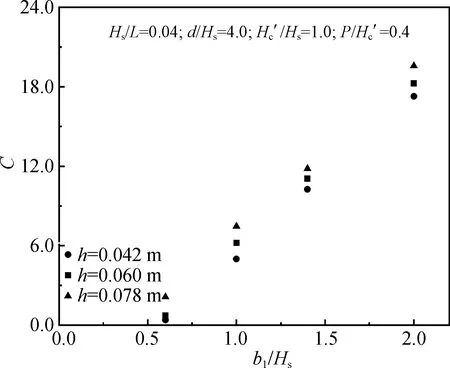
圖9 C隨b1/Hs的變化趨勢

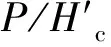
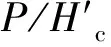
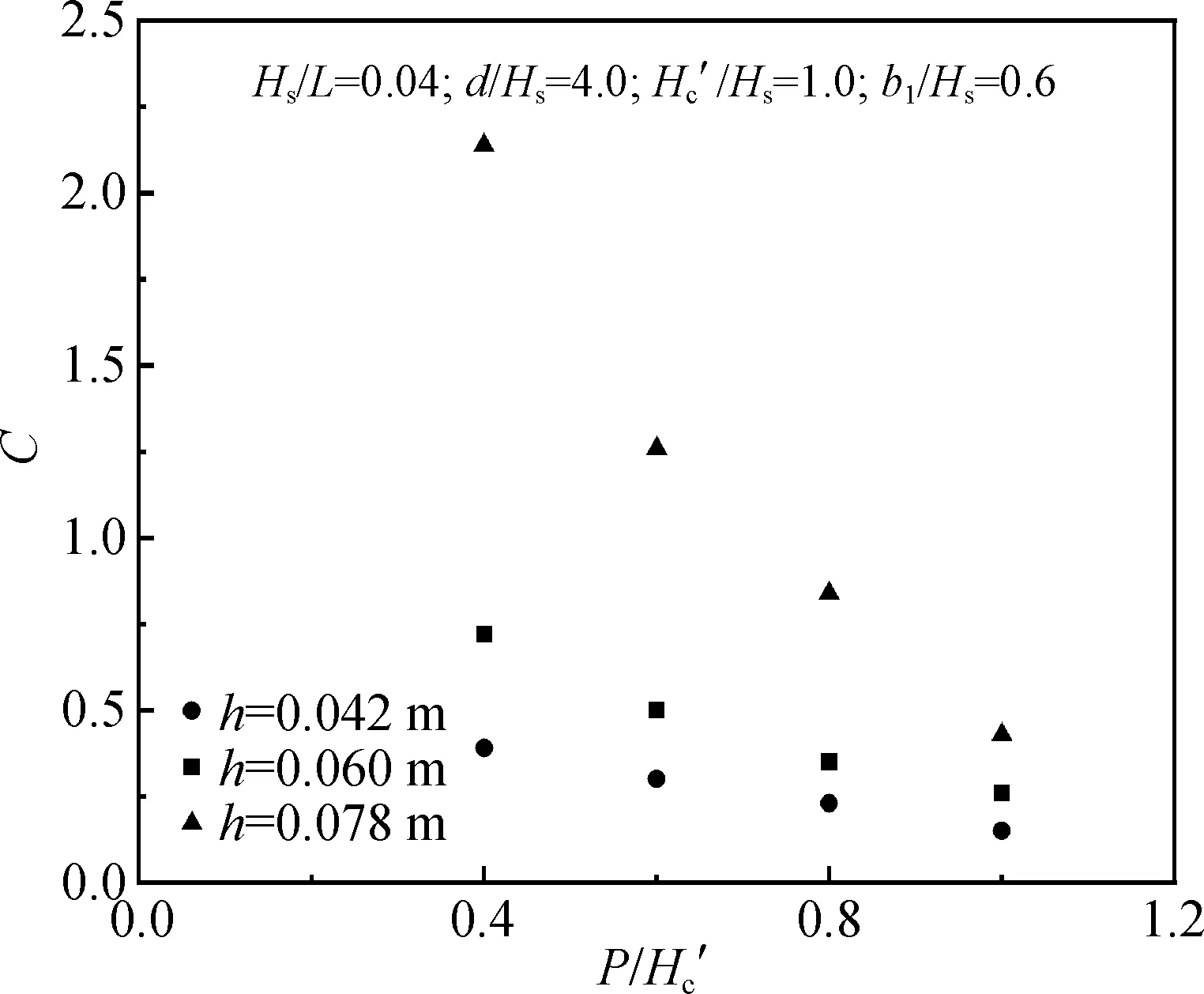
圖10 C隨的變化趨勢

3.1.6C隨h/Hs的變化趨勢

僅改變h/Hs的取值，圖11給出了C值隨相對塊體尺寸變化的趨勢。在圖11所示范圍內，h/Hs增大時C也逐漸增大，呈指數函數關系。

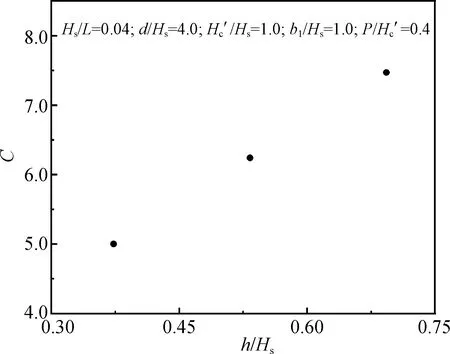
圖11 C隨h/Hs的變化趨勢

3.1.7C值計算關系式(m=2.0)

采用表3的C率定值，基于非線性擬合法，給出坡度系數m=2.0時系數C的計算關系式為：

(6)

3.2 坡度系數m=2.5的C值計算關系式

3.2.1C隨Hs/L的變化趨勢

僅改變Hs/L的取值，圖12給出了C值隨波陡變化的趨勢。在圖12所示范圍內，Hs/L增大時C也逐漸增大，呈指數函數關系。

圖12 C隨Hs/L的變化趨勢

3.2.2C隨d/Hs的變化趨勢

僅改變d/Hs的取值，圖13給出了C值隨相對水深變化的趨勢。在圖13所示范圍內，d/Hs增大時C也逐漸增大，呈對數函數關系。

圖13 C隨d/Hs的變化趨勢

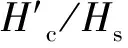
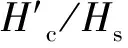
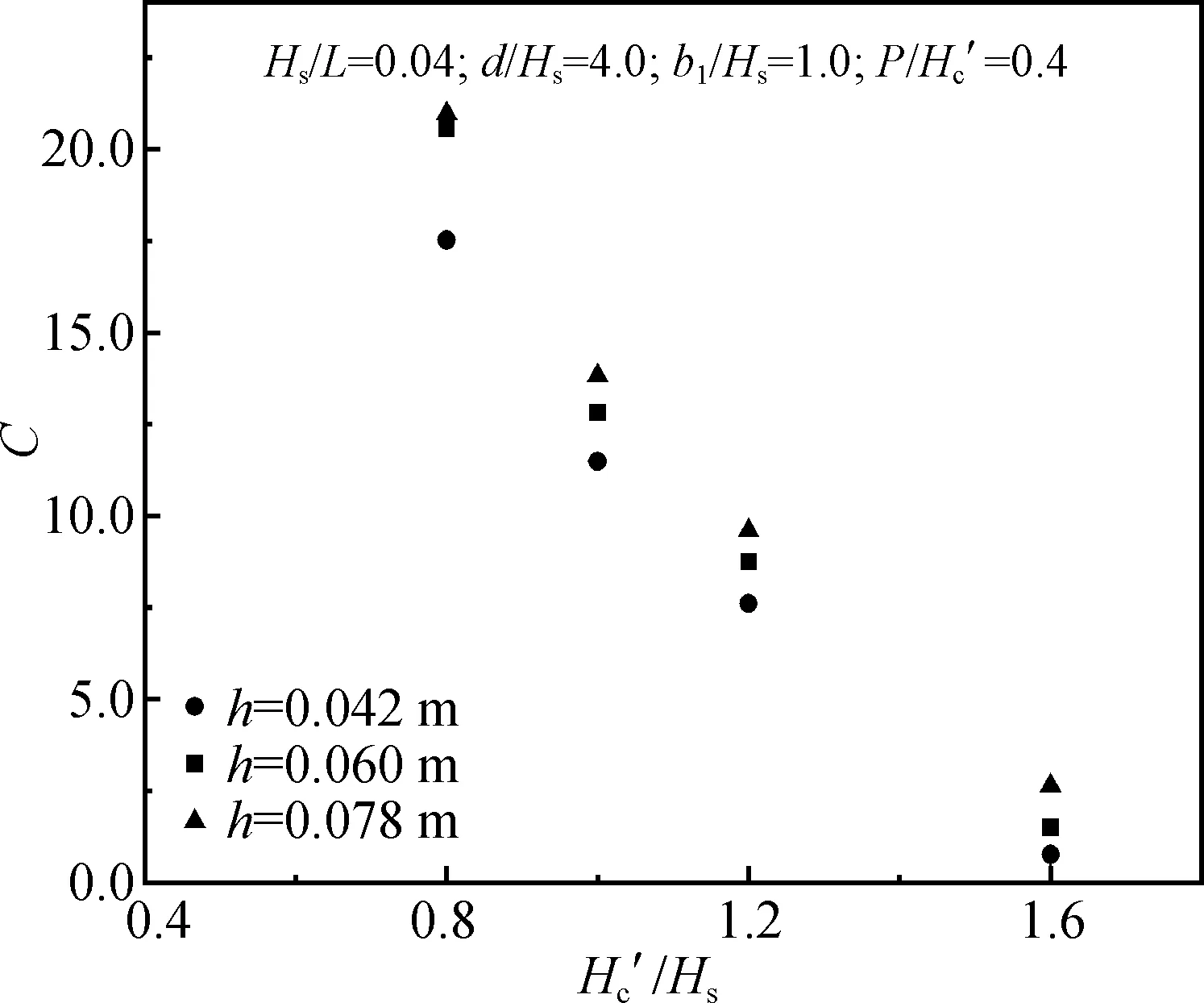
圖14 C隨的變化趨勢

3.2.4C隨b1/Hs的變化趨勢

僅改變b1/Hs的取值，圖15給出了C值隨相對坡肩寬度變化的趨勢。在圖15所示范圍內，b1/Hs增大時C也逐漸增大，呈指數函數關系。

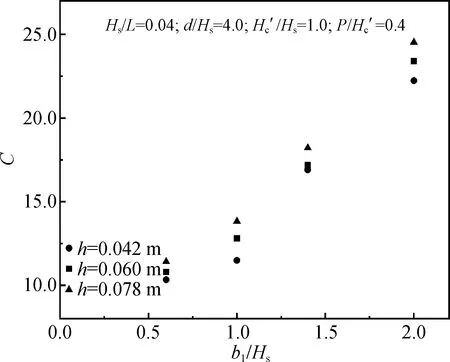
圖15 C隨b1/Hs的變化趨勢

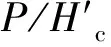
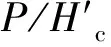
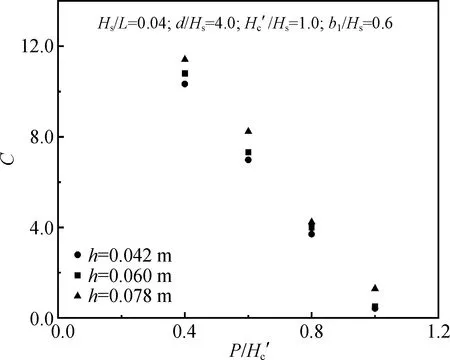
圖16 C隨的變化趨勢

3.2.6C隨h/Hs的變化趨勢

僅改變h/Hs的取值，圖17給出了C值隨相對塊體尺寸變化的趨勢。在圖17所示范圍內，h/Hs增大時C也逐漸增大，呈指數函數關系。

圖17 C隨h/Hs的變化趨勢

3.2.7C值計算關系式(m=2.5)

采用表4的C率定值，基于非線性擬合法，給出坡度系數m=2.5時系數C的計算關系式為：

(7)

3.3 C值計算關系式的驗證

3.3.1 計算關系式的準確性驗證

為驗證文中給出的式(6)、(7)準確性，將公式計算出的C值記為C計算值，兩種坡度m=2.0、2.5下的C計算值與C率定值對比如圖18所示，可以看出兩者吻合較好，表明式(6)、(7)能較準確計算出每個工況系數C的值。

圖18 C率定值與C計算值

3.3.2 計算關系式的有效性驗證

為驗證文中給出的式(6)、(7)系數C計算值的有效性，將公式計算出的C計算值帶入FLUENT軟件中數值模擬出的越浪量Q值與相同工況下的物模試驗[9]越浪量Q值進行對比，如圖19所示，可以看出C計算值可有效數值模擬出相應工況下的越浪量，這表明了式(6)、(7)可有效應用于扭王字塊體斜坡堤越浪量的數值模擬計算，繼而可供實際工程的設計應用。