輸電塔-線體系的風致動力穩定性分析

凌曉斌， 杜偉， 周轉， 高玄， 齊益， 趙寶成

(1.國網黃山供電公司， 黃山 245000； 2.安徽華電工程咨詢設計有限公司， 合肥 230061; 3.蘇州科技大學土木工程學院， 蘇州 215011)

架空輸電線路主要由輸電塔和導、地線構成。隨著經濟、技術的發展，架空輸電線路的覆蓋面日益擴大，其高度與跨度不斷增加，輸電塔-線結構體系同時承載了高聳和大跨柔性結構的安全需求。目前，輸電塔和導地線風荷載的計算主要根據《架空輸電線路荷載規范》(DL/T 5551—2018)[1]的等效靜力方法，利用陣風系數和檔距折減系數考慮脈動風對導地線風載影響、利用風荷載脈動折減系數考慮結構敏感性和塔線疊加相關性。然而輸電塔結構在豎向力和側向力共同作用時，其抗側移能力會因結構動力失穩而顯著降低，基于靜力計算的強度設計不能反映結構的穩定性。因此，輸電塔-線結構在風荷載作用下的動力穩定性研究具重要的工程意義。

現有輸電塔研究主要包括輸電塔優化設計方法[2]、各類型輸電塔-線體系風致的動力響應[3-6]、多因素與風載耦合條件下的動力響應[7-8]、導線舞動動力特征[9-10]及臺風等極端天氣下的動力響應[11-13]。李慶偉等[14]采用B-R(Budiansky-Rot)準則和增量動力分析法(increment dynamic analysis, IDA)結合位移相等原則分析了沈陽某輸電塔在風載作用下的動力穩定性。夏闖娜[15]利用ANSYS有限元分析了輸電塔-線體系的非線性靜力穩定性。李正良等[16]利用氣彈性風洞試驗和有限元模擬研究了輸電塔線體系風振響應，對現行規范風振系數計算方法提出了改進建議。

目前，輸電塔-線結構的風致動力穩定研究尚不成熟。為此，基于B-R準則[17]研究不同水平檔距輸電塔-線結構的風致動力穩定性。通過桿塔頂部側移比、桿件應力、導地線掛線點反力、張力和振幅變化規律分析了塔-線相互作用及結構動力失穩前、后的受力特征。根據非線性靜力與動力失穩塔頂側移比相等原則得到了不水平檔距塔-線結構動力失穩臨界平均風速，分析了水平檔距對輸電塔動力失穩的影響。

1 有限元建模

研究輸電塔為安徽某220 kV貓頭型懸垂塔，桿塔兩側高差為0，水平檔距相同。輸電塔呼稱高42 m，總高49 m，主材、斜材與輔材均為等邊角鋼，主材和部分斜材為Q345鋼材，其余為Q235鋼材。桿塔單線如圖1所示，導、地線型號分別為JL/G1A-400/35、JLB20A-150，參數信息如表1所示。

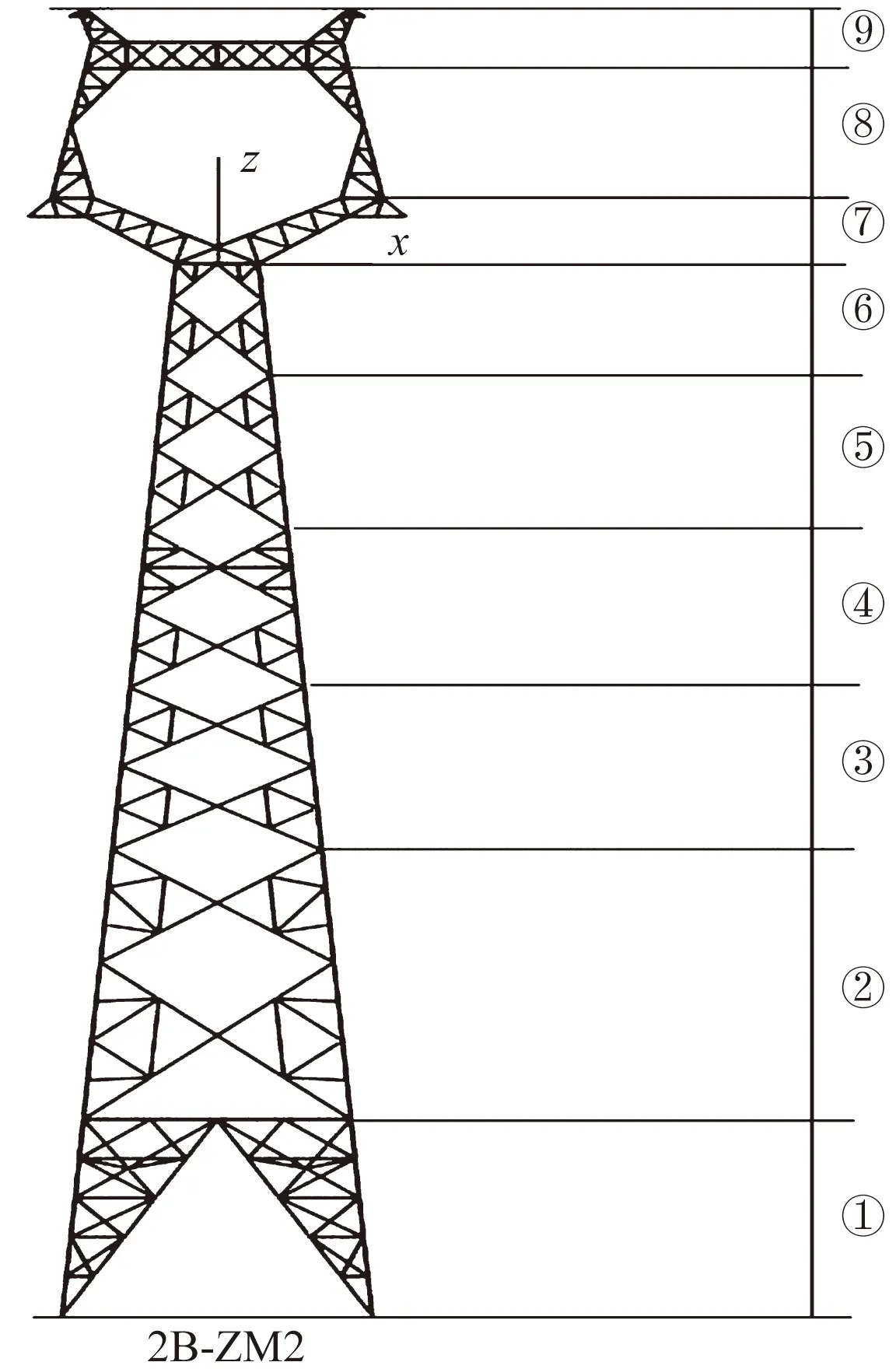
①～⑨為輸電塔9區段編號圖1 輸電塔單線圖Fig.1 Single line diagram of transmission tower

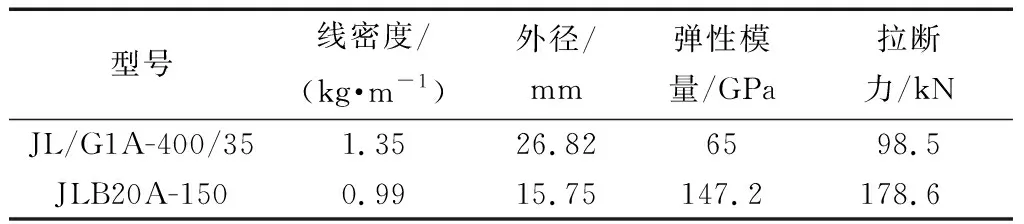
表1 導地線參數Table 1 Conductor and ground wire parameters

塔-線結構模型為單塔兩檔，利用ABAQUS軟件進行有限元模擬，有限元模型如圖2所示，x、y和z方向分別對應導地線縱向、風攻向和塔高方向。桿塔單元為梁單元B31，導、地線單元為桁架單元T3D2，設定T3D2單元只能受拉；材料本構模型為理想彈塑性；塔腳為剛接，導地線兩端為鉸支座，中點與輸電塔懸掛點用屬性為“Join”的連接單元連接，忽略絕緣子串響應。桿塔梁單元截面尺寸及截面方向與實際一致，材料塑性應力取屈服強度；導地線塑性應力取拉斷力對應應力，地線截面面積與實際相同，二分裂導線等效為一整體[18]，材料阻尼α取0.1、β取0。

有限元計算包括塔-線在重力下導地線找行分析和塔-線在風載下的非線性隱式動力分析。找形分析采用直接迭代法[19]。輸電塔和導地線重力包括自重和覆冰荷載，其中覆冰荷載按照桿件覆冰厚度等效為桿件密度，以重力方式施加[20]。桿塔和導線覆冰厚度為15 mm，地線覆冰厚度為20 mm。風載響應采用非線性隱式動力分析，將輸電塔按垂直高度分為9段(圖1)，每段按其中點高度計算風壓，將各高度脈動風速時程與平均風速疊加并考慮輸電塔的體型系數得到風壓，將風壓乘以該段受風面積并除以加載單元節點數，得到單元節點上的力。桿塔9區段中點高度分別為3.5、13.5、21、27、30、36、39.5、43.5、47.5 m，導地線節點力計算方法與桿塔相同，風壓計算高度取懸掛高度與弧垂高度的平均值。風向角為0°，加載方向為y方向。脈動風速時程采用線性濾波法中的自回歸法(auto-regressive，A-R)模擬[21]，利用MATLAB計算得到高50 m的空間脈動風速時程。

塔-線體系的動力穩定研究包括遞增平均風速IDA分析和基于弧長法(Riks)的非線性靜力穩定分析。塔-線水平檔距分別取250、300、350、400、450 m，IDA分析對應10 m高度平均風速為20、22、24、26、28、30 m/s。Riks分析用于與IDA分析結果對比，平均風速取28 m/s，風壓依據文獻[1]計算。塔-線算例名稱及其設計參數如表2所示。

圖2 輸電塔-線結構有限元模型Fig.2 Finite element model of transmission tower line structure

導地線找形分析采用直接迭代法：①首先初步確定導地線原長建立直線模型，在導地線兩端施加一定預拉力；②施加導地線和桿塔重力；③釋放預拉力；④判斷是導地線弧垂、張力與實際間的誤差是否滿足，若不滿足則重復①～③直至滿足。為提高建模和找形效率，采用Python編寫代碼完成ABAQUS的建模-找形-迭代，將導地線弧垂與張力作為判斷條件，規定有限元計算與實際誤差小于5%。檔距250、300、350、400、450 m塔-線結構導、地線找形結果如圖3所示，弧垂分別為6.15、8.74、12.1、15.9、20.2 m，與工程實際測量弧垂誤差小于2%。

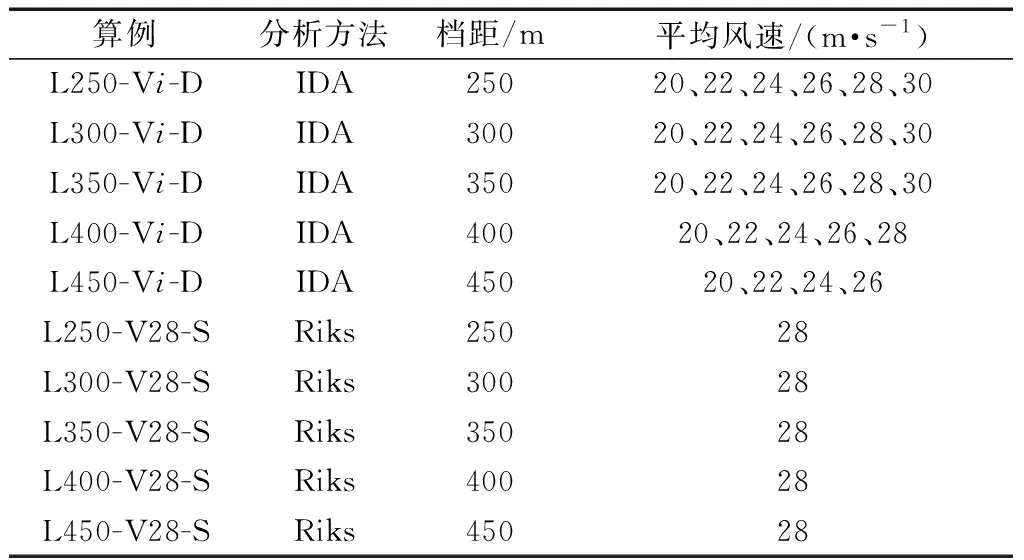
表2 塔-線算例參數Table 2 Tower line example parameters

圖3 導地線找形結果Fig.3 Shape results of conductor and shield wires

A-R法風速時程模擬基本假設為：①任意一點處平均風速不隨時間改變；②脈動風速時程是零均值、平穩高斯過程；③風速時程具有空間相關性；④不同高度處的脈動風速作用同相。脈動風時程的目標功率譜為Davenport功率譜，相干函數采用Davenport相干函數，自回歸階數取4。同一平均風速包括50 m高度內、增量0.5 m的100條脈動風速時程，每條脈動風速時程持時204.8 s，時間間隔0.1 s，取0～200 s作為荷載數據。圖4(a)和圖4(b)分別為高度10 m處風速時程及其自功率密度譜與目標功率譜的對比，可以看出風速時程符合脈動風特征，其自功率譜變化趨勢與目標譜基本一致，且目標譜基本位于模擬譜中部，說明該空間風速時程可用于本研究。

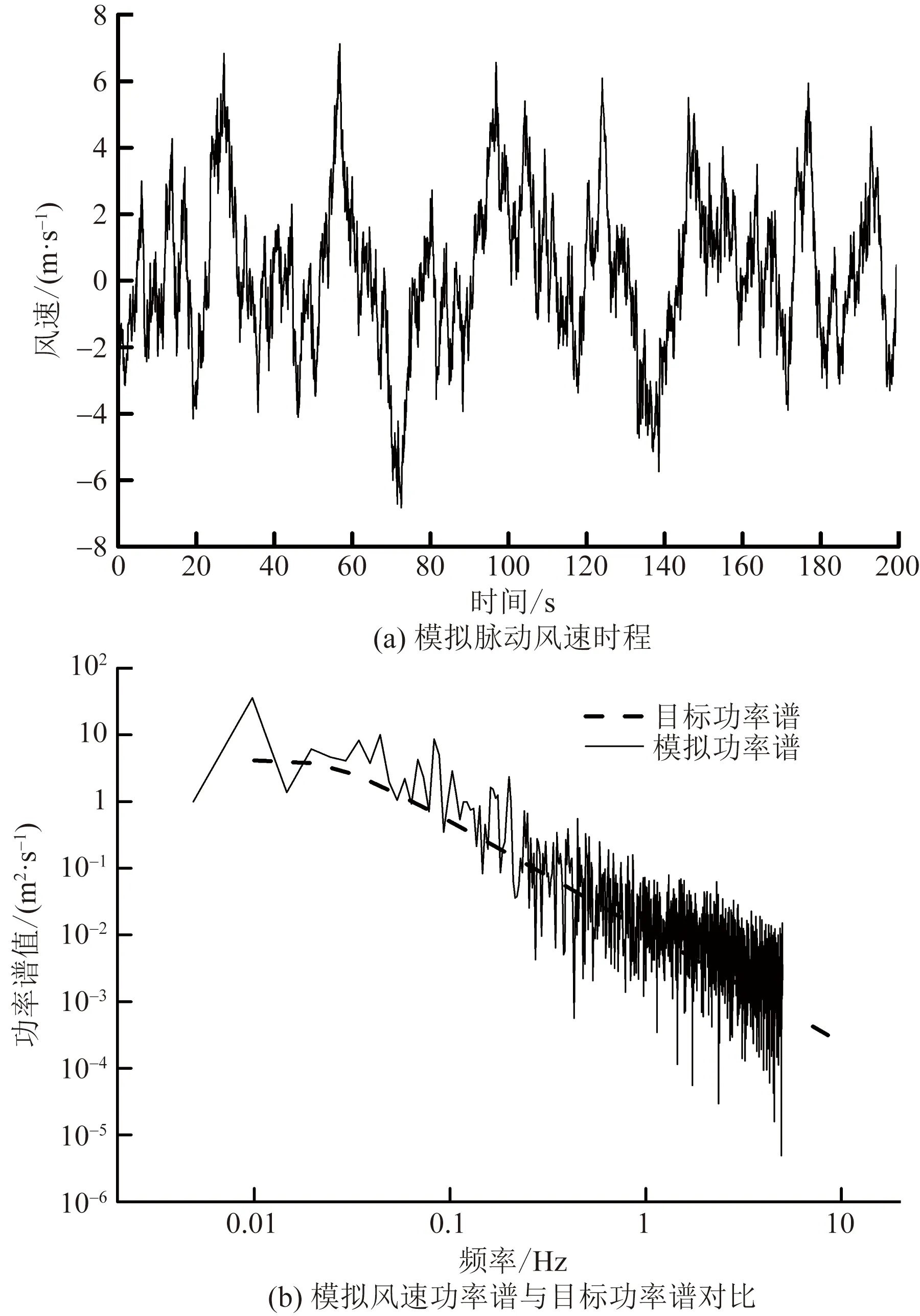
圖4 脈動風模擬對比Fig.4 Comparison of fluctuating wind simulation

2 輸電塔-線結構失穩特征

以300 m檔距為例，結合IDA和Riks分析塔-線結構的風致響應及動力失穩前、后的受力特征。圖5為L300-V20-D～L300-V30-D塔頂側移比時程曲線，塔頂側移比D/H隨時間變化呈脈動趨勢，D/H-時間曲線的振幅隨平均風速增加而增大。L300-V20-D塔頂側移比在107.2 s時達到最大值0.41%，L300-V22-D塔頂側移比在107.8 s時達到最大值0.58%，L300-V24-D塔頂側移比在155.3 s時

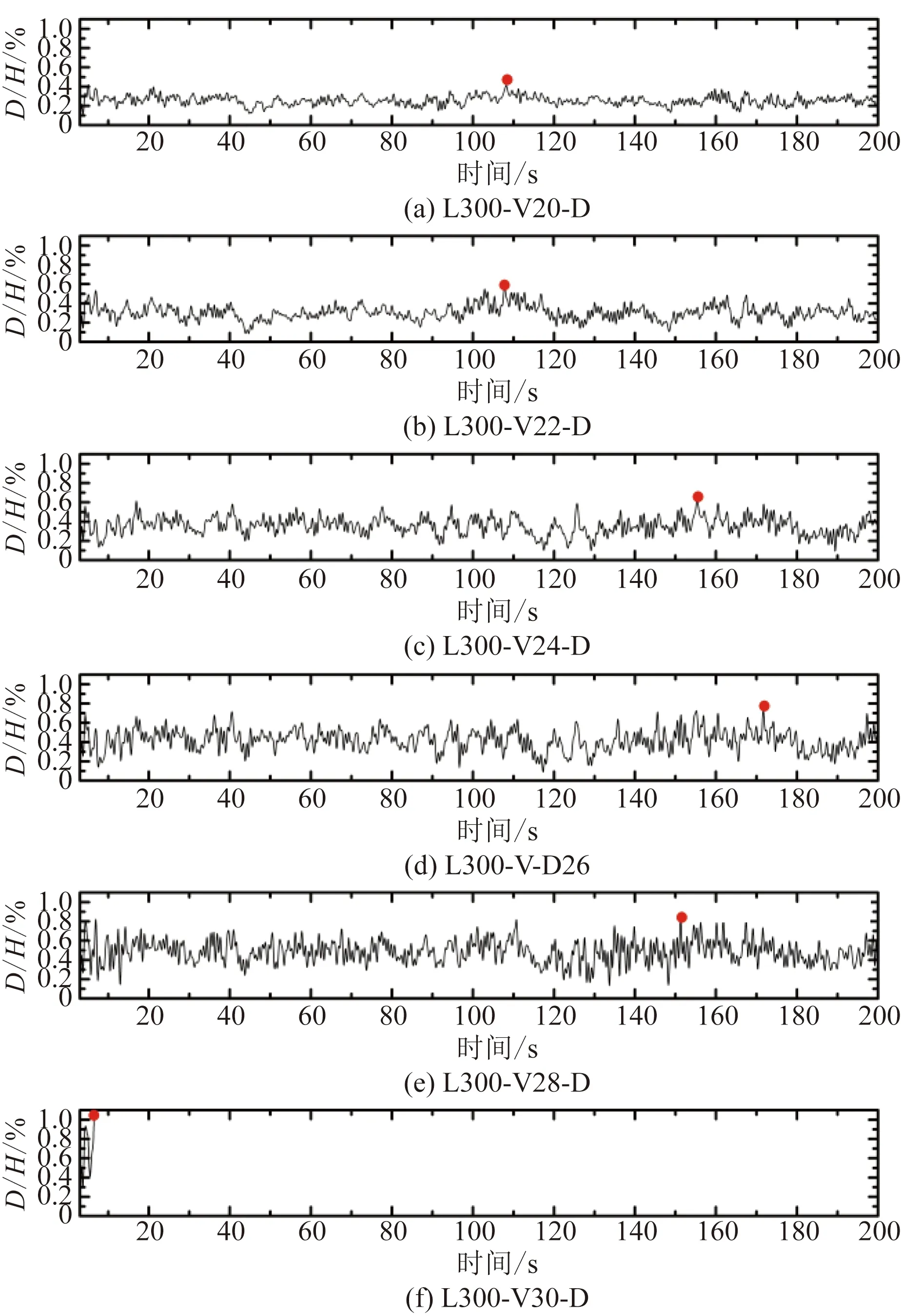
D/H為塔頂側移比，其中，D為塔頂側移，H為塔高；紅點為塔頂側移比最大值圖5 L300-Vi-D塔頂側移比時程Fig.5 L300-Vi-D tower top drift ratio time-histories

達到最大值0.62%，L300-V26-D塔頂側移比在171.7 s時達到最大值0.74%，L300-V28-D塔頂側移比在151.3 s時達到最大值0.84%，L300-V30-D塔頂側移比在6.4s時達到最大值0.98%。

分析各算例應力分布知，塔頂側移比較大導致塔身受壓側主材應力較大，圖6顯示了L300-Vi-D受力較大桿件的Mises應力時程曲線，受力較大桿件均為塔身底層受壓側主材。可以看出，各算例桿件應力變化規律及最大值時刻與塔頂側移比時程曲線幾乎相同。值得注意的是：L300-V26-D桿件應力最大值328.5 MPa接近材料屈服強度；L300-V28-D桿件應力在4.3、6.8、110.8、161.8 s均達到材料屈服強度345 MPa；L300-V30-D桿件在6.4 s第二次達到屈服強度后開始下降。

分析各算例導地線受力情況知，上相導線掛線點反力及其張力較大，相應時程曲線分別如圖7、圖8所示。可以看出，上相導線響應速度要明顯滯后于桿塔，隨著平均風速增加，上相導線掛點反力及張力幅值逐漸增大。如圖7所示，L300-V20 -D～L300-V30-D上相導線掛線點反力最大值分別為17.8、21.2、

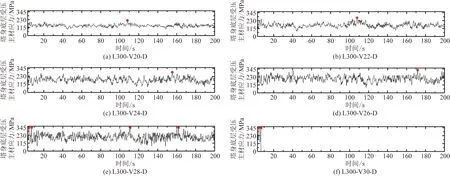
紅點為應力最大值圖6 L300-Vi-D塔身底部受壓桿件應力時程Fig.6 Mises stress time-histories of L300-Vi-D pressure bar at the bottom of tower body

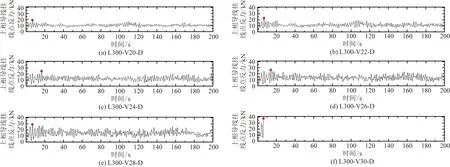
紅點為表示掛線點反力最大值時刻與桿塔頂側移比及塔身底層受壓主材應力最大時刻不一致圖7 L300-Vi-D上相導線掛線點反力時程Fig.7 Reaction force time-histories of phase conductor hanging point on L300-Vi-D

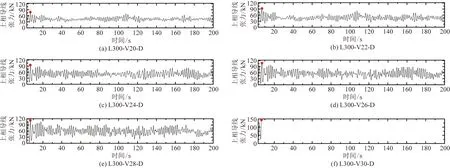
紅點表示最大值時刻基本集中在7 s左右，與掛點反力最大值時刻不一致圖8 L300-Vi-D上相導線張力時程Fig.8 Conductor tension time-histories of L300-Vi-D

22.5、24.5、27.6、37.2 kN，掛線點反力最大值時刻與桿塔頂側移比及塔身底層受壓主材應力最大時刻不一致。如圖8所示，L300-V20-D～L300-V30-D上相導線張力時程曲線變化規律與其掛線點反力時程曲線變化規律相近，張力最大值分別為74.9、90.0、97.7、107.6、118.6、134.1 kN，最大值時刻基本集中在7 s左右，與掛點反力最大值時刻不一致。

導地線在風荷載作用下的振幅基本與弧垂相同，隨平均風速的增大略有增加。L300-V24-D上相導線運動軌跡如圖9所示，導線在風荷載和重力作用下向沿塔高和風攻方向運動，最大振幅約為11.6 m，略大于弧垂8.8 m。

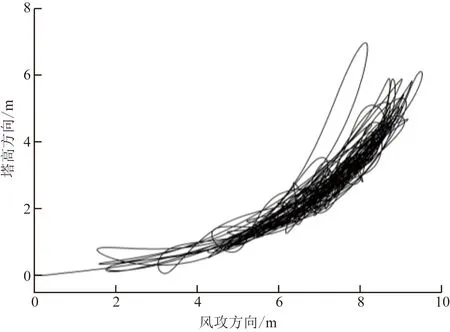
圖9 L300-V24-D上相導線運動軌跡Fig.9 Upper conductor motion curve of L300-V24-D

分析可知，桿塔和導地線在風荷載下的響應存在明顯差別，因此分析二者響應較大時刻桿塔的應力分布規律。圖10(a)為L300-V26-D上相導線掛點反力最大值時刻桿塔Mises應力分布，可以看出掛線點橫隔主材已達到屈服強度345 MPa。圖10(b)為L300-V28-D塔身底層受壓主材應力最大時刻桿塔Mises應力分布，可以看出塔身底層受壓側主材大部分達到屈服強度。圖10(c)為L300-V30-D 6.4 s時桿塔Mises應力分布，此時塔身底層至三層受壓側主材、斜材嚴重變形，橫擔掛線處主材達到屈服強度。

塔-線結構動力失穩的過程可總結為掛線點主材屈服-塔身底層受壓主材屈服-塔頂側移比增大-桿塔底部嚴重變形，而桿塔失穩的臨界狀態較難判斷。圖11對比了桿塔Riks(L300-V28-S)與IDA分析得到的標準高度平均風速-塔頂側移比(D/H)曲線，L300-V28-S在平均風速24.8 m/s時出現拐點，塔身底層受壓側主材屈服；在風速25.2 m/s時Riks運算結束，塔身頂層受壓側主材彈塑性屈曲，對應塔頂側移比0.57%。IDA曲線在前期與Riks曲線幾乎重合，在平均風速20 m/s時出現拐點，此后二者差別增大。與動力失穩特征相比，非線性靜力失穩前桿塔掛線點周邊桿件未進入塑性，且桿塔受壓側主材進入塑性較早。根據位移相等原則，以塔頂側移比0.57%定位IDA曲線上的平均風速，得到檔距300 m塔-線結構動力失穩臨界風速為22.8 m/s。

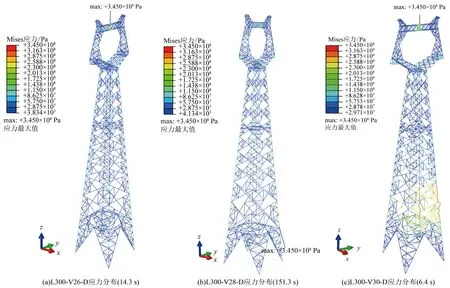
圖10 應力分布Fig.10 Stress distribution

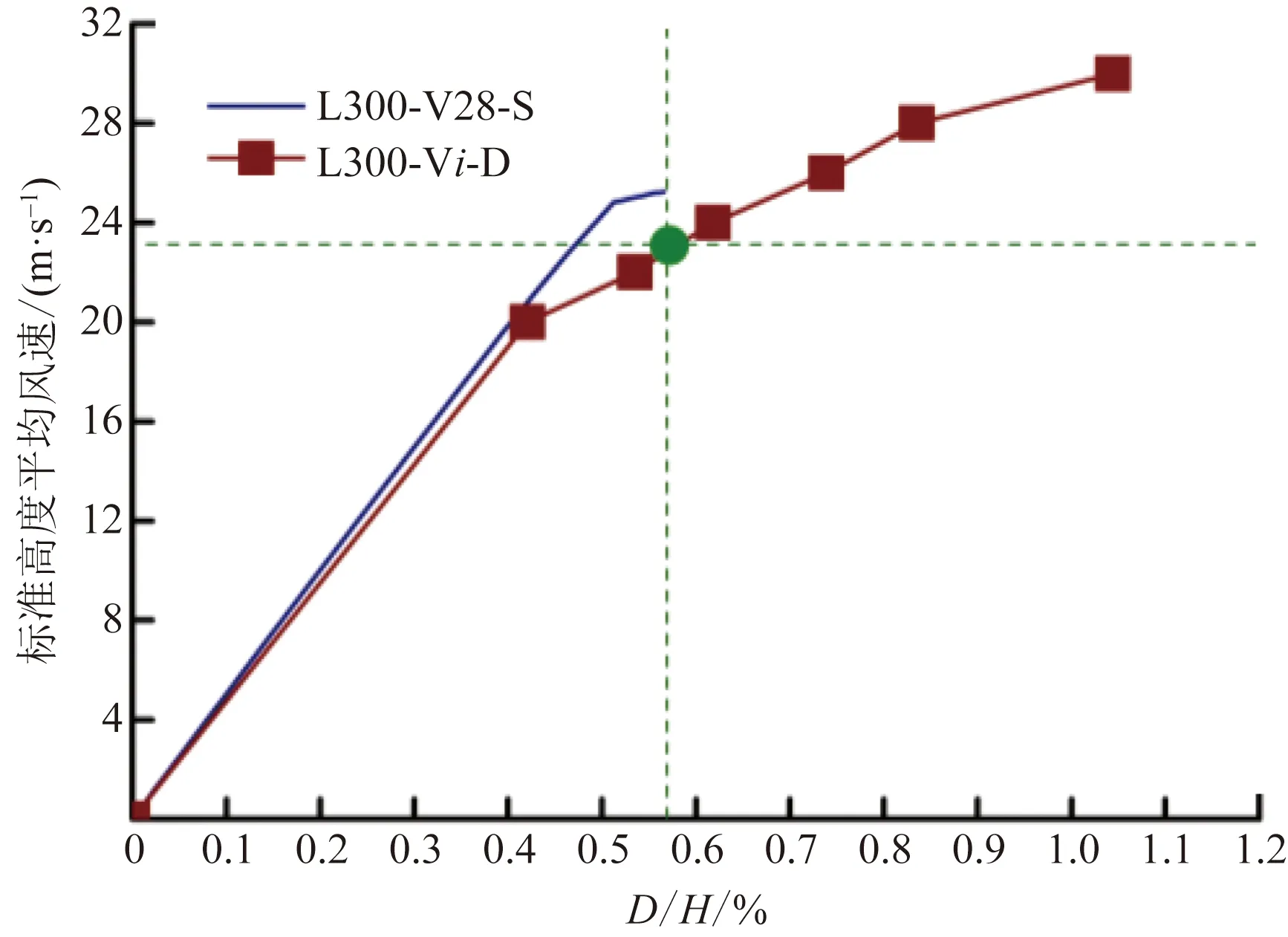
圖11 300 m檔距標準高度平均風速-D/H曲線Fig.11 Basic wind speed-D/H curves of 300 m span

3 塔-線動力穩定參數影響分析

綜合IDA與Riks運算結果，分析不同檔距輸電塔-線結構的動力穩定，通過Riks與IDA臨界塔頂側移比相等原則得到輸電塔動力失穩臨界平均風速。圖12(a)為L250標準高度平均風速-D/H曲線，L250-V28-S曲線在前期線性增長，風速為21.8 m/s時出現拐點，塔頂側移比達到0.7%后，非線性靜力穩定運算停止，對應風速27.7 m/s。L250-V20-D～L250-V30-D塔頂側移最大值基本維持線性增長，當平均風速為30 m/s時塔頂側移比為1.0%，桿塔底層嚴重變形，非線性動力運算停止。Riks與IDA曲線第一拐點對應風速基本一致，但Riks曲線斜率較小，可見塔-線動力相互作用在結構彈性階段對穩定有利；當平均風速超過22 m/s后IDA曲線值小于Riks曲線值；按位移等效原則可得L250塔-線臨界平均風速為23.9 m/s。

圖12(b)為L350標準高度平均風速-D/H曲線，L350-V28-S曲線在前期維持線性增長，塔頂側移比達到0.56%后，非線性靜力穩定運算停止，對應平均風速24.2 m/s。L350-V20 -D～L350-V30-D塔頂側移最大值基本保持線性增長，當平均風速為30 m/s時，非線性動力運算停止，塔頂側移比為1.0%，曲線略有突變。Riks與IDA曲線在前期基本重合，可見塔-線動力相互作用在結構彈性階段并不明顯；當平均風速超過20 m/s后IDA曲線值小于Riks曲線值；按位移等效原則可得L350塔-線臨界平均風速為21.7 m/s。塔-線算例L400 Riks與IDA曲線[圖12(c)]變化趨勢及差別與L350分析結果類似，L400 IDA曲線最大風速為28 m/s，Riks曲線最大平均風速為23.4 m/s，塔-線臨界平均風速為21.2 m/s，小于L350臨界平均風速。

L450標準高度平均風速-D/H曲線如圖12(d)所示，L450-V28-S曲線在前期線性增長，風速20 m/s

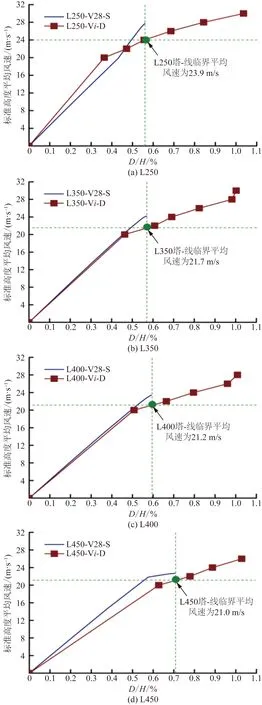
圖12 標準高度平均風速-塔頂側移比曲線Fig.12 Basic wind speed-D/H curves

出現拐點，塔頂側移比達到0.56%后，非線性靜力穩定運算停止，對應風速22.7 m/s。L450-V20-D～L450-V30-D塔頂側移最大值基本維持線性增長，當平均風速為26 m/s時，塔頂側移比為1.0%，動力運算停止。L450 IDA曲線值始終小于Riks曲線值，可見塔-線動力相互作用對結構穩定不利；按位移等效原則可得L450塔-線臨界平均風速為21.0 m/s。

對比Riks和IDA曲線可知，隨著檔距增大，塔-線結構的前期響應經歷了靜力大于動力、靜力約等于動力、靜力小于動力的演變過程；在后期響應中塔-線的動力響應均大于靜力響應。L250～L450塔-線靜力與失穩臨界平均風速對比如表3所示，靜力和動力失穩平均風速隨檔距增大而降低，靜力與動力失穩平均風速比值隨檔距變化基本維持在1.1左右。

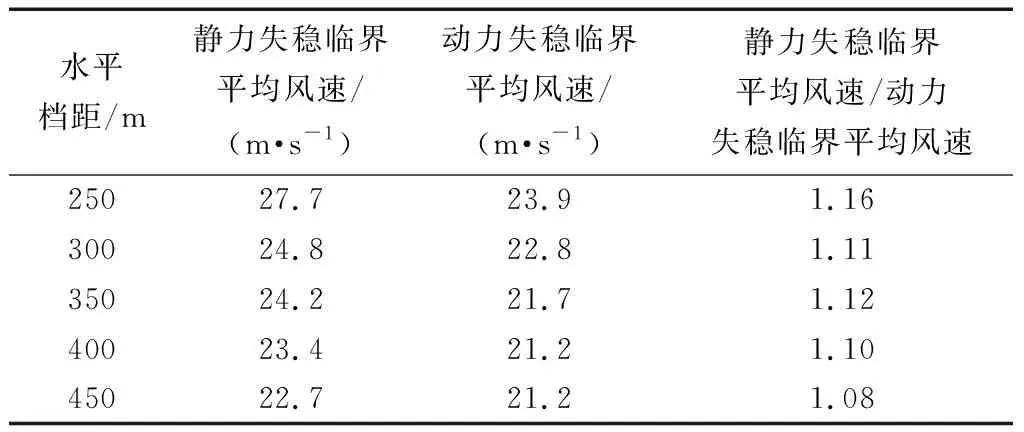
表3 塔-線靜力與動力失穩臨界平均風速對比Table 3 Comparison of critical wind speed between static and dynamic analyses

4 導地線動力響應參數影響分析

通過各算例上相導線的掛線點反力、張力和振幅最大值分析水平檔距和平均風速對導地線動力響應的影響。圖13為上相導線掛線點反力峰值-平均風速曲線，掛線點反力峰值隨平均風速增加而增大；同一平均風速下掛線點反力峰值隨檔距增大而增加，當IDA接近最大風速時(L250、L300、L350為30 m/s，L400為28 m/s，L450為26 m/s)掛線點反力峰值基本一致，約為35 kN，符合第3節分析的塔-線動力失穩特征。

上相導線張力峰值-平均風速曲線如圖14所示，導線張力峰值隨平均風速增加而增大；同一平均風速下導線張力峰值隨檔距增大而減小。L250～L450導地線的初始張力相同，但剛度不同，固在風荷載、自重和覆冰荷載共同作用下檔距越大導線張力越小。L250～L450上相導線振幅隨平均風速變化規律如圖15所示，各檔距導線振幅隨風速增大略有增加，振幅峰值基本略大于弧垂，固檔距越大導線振幅越大。

桿塔與導地線相互作用主要反映在掛線點反力和二者運動特性的差異。增加塔-線結構檔距，使得桿塔掛線點反力增大，也使得導地線張力減小、導地線振幅增大，導致導地線與桿塔運動特性的差異變大。綜合來看，水平檔距對于塔、線相互作用及桿塔動力穩定的影響較大，但對輸電塔動力放大效應影響不明顯。

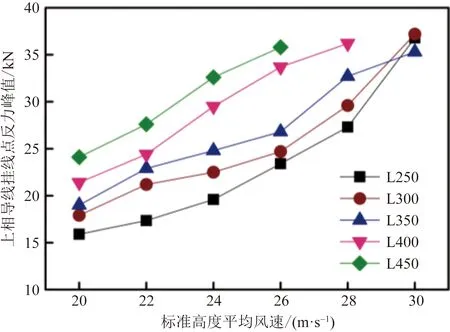
圖13 掛線點反力峰值-標準高度平均風速曲線Fig.13 Hanging reaction peak force-basic wind speed curves

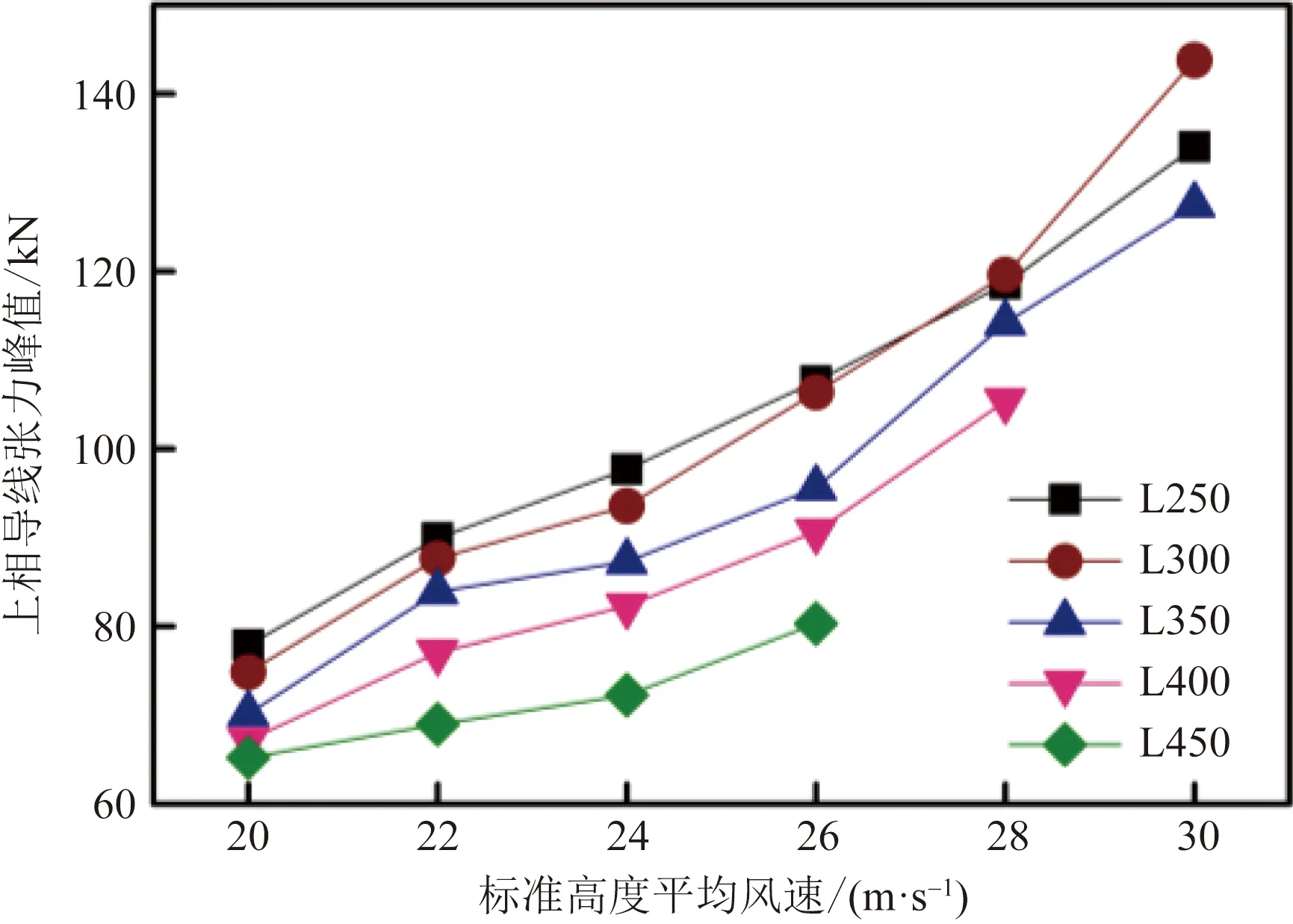
圖14 導線張力峰值-標準高度平均風速曲線Fig.14 Conductor peak tension-basic wind speed curves

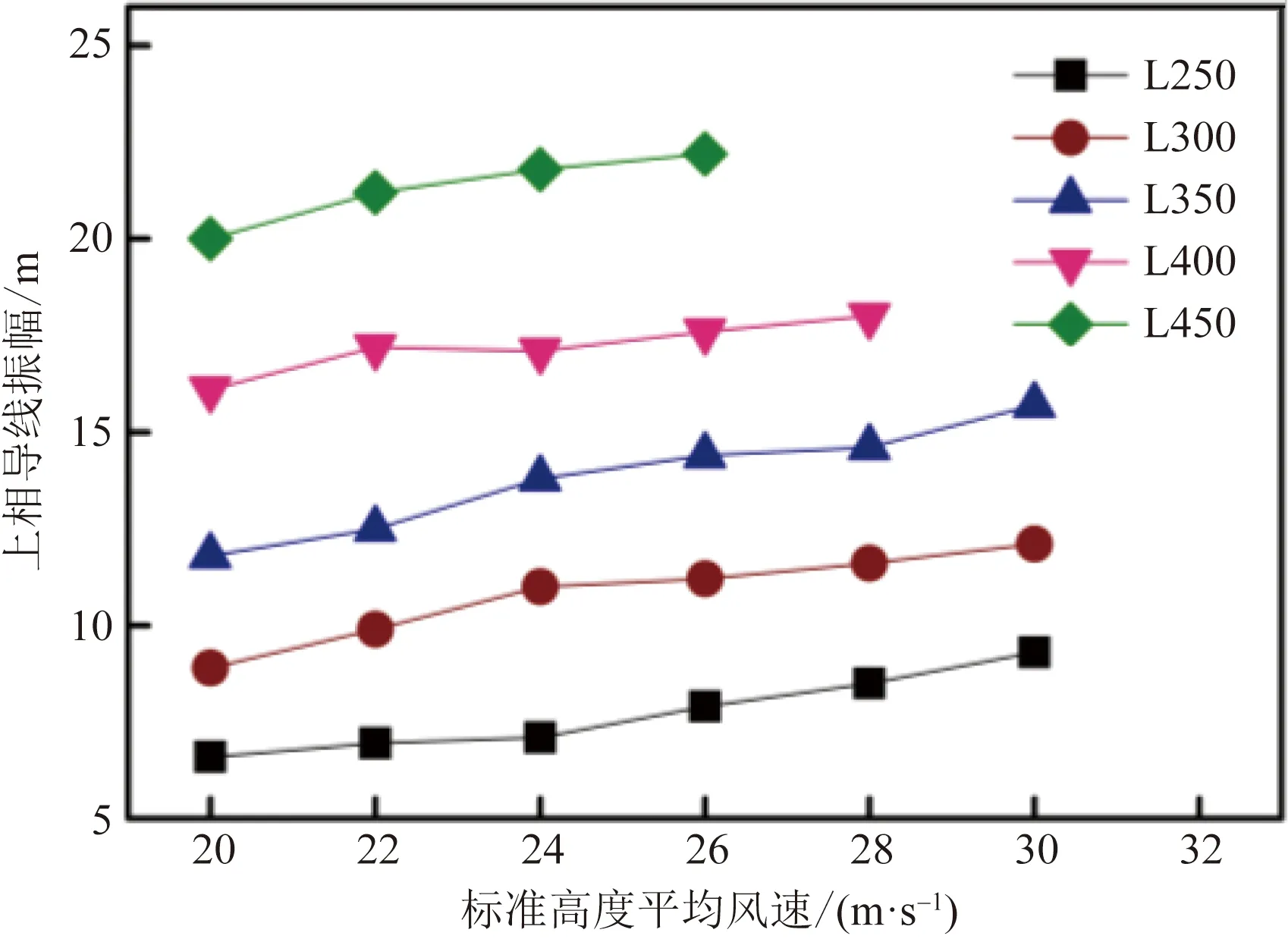
圖15 導線振幅-標準高度平均風速曲線Fig.15 Peak conductor amplitude-basic wind speed curves

5 結論

結合增量動力分析法和弧長法對不同水平檔距塔-線結構在風荷載作用下的動力穩定進行了研究，通過桿塔和上相導線的動態響應分析了塔-線結構的動力失穩特征，有限元參數影響分析了塔-線的動力穩定。得出如下主要結論。

(1)塔-線結構動力失穩的過程為掛線點主材屈服-塔身底層受壓主材屈服-塔頂側移比增大-桿塔底部嚴重變形。

(2)隨著塔-線水平檔距增加，輸電塔頂部側移比增大，掛線點反力增大，導地線張力減小，導地線振幅增大，動力失穩臨界平均風速減小。

(3)水平檔距對于塔、線相互作用及桿塔動力穩定的影響較大，但對輸電塔動力放大效應影響不明顯，靜力與動力穩定臨界平均風速比值約為1.1。