建構益智課堂 關注思維發展

曾蓮秀 王太清

教學內容：

人教版數學義務教育教科書六年級上冊數學廣角——數與形教學內容與自制益智器具“魔術拼板”融合教學。

教學目標：

1.在具體情境中讓學生理解數與形的對應關系，會利用圖形來解決一些有關數的計算問題，會利用數來解決有關圖形的辨析問題。

2.在數與形的互相轉換中，讓學生欣賞數形結合的美妙，感悟數與形的密切聯系。

教學過程：

一、談話激趣，揭示課題

（教師播放“魔術拼板”視頻）

師：你們看到了什么？是啊，像變魔術似的，還是用這四塊板，看起來都拼成同樣大的三角形，可第二次拼圖中怎么少了一塊？出現一個空的小正方形呢！要破解這個魔術，咱們先來學習“數與形”。

二、理解體會“數缺形時少直觀”

1.探究“從1開始，連續奇數相加的和等于加數個數的平方”

課件出示填空題：觀察題中加數有什么特點，并填出括號中的數。

1+3=（? ）=（? ）2

1+3+5=（? ）=（? ）2

1+3+5+7=（? ）=（? ）2

1+3+5+7+9=（? ）=（? ?）2

師：這些算式有什么特點？

生：連續奇數相加，從1開始，和都可以看成幾的平方。

生（小結）：從1開始，連續奇數相加的和等于加數個數的平方。

師：這些都是“數”（板貼“數”）。現在我們將這些“數”用“形”表示出來（板貼“形”）。老師帶來一些小方塊，我用1個方塊表示“1”，那“3”就可用3個方塊表示，5個方塊表示“5”。

師：1+3+5=3×3。看到3×3，你們能想到一個什么形？

生：邊長為3的正方形。

（學生用不同顏色的方塊卡片拼正方形，教師引導學生觀察有規律、無規律的圖案，比較優劣）

師：按照此規律，如果再加一個數是哪個數？方塊該怎么擺？

（學生繼續操作并用手勢比畫擺放區域）

師：這些圖形漂亮嗎？有規律的圖形很漂亮，漂亮的圖形會說話，看，這幅圖好像在說什么？（課件出示1+3+5+7=4×4，1+3+5+7+9=5×5）

師：這么有規律地擺放，拼出的正方形的邊長與加數的個數有什么關系？小方塊的總個數與拼出的正方形面積有什么關系？

師：同學們很會歸納推理，真棒！老師有個問題，沒有圖你們會算這些題嗎？（生：會）那有個圖有啥用？

生：更清楚，更直觀。

師：是啊！通過形的輔助，就能很直觀地發現得數的規律。而以形助數，就形象直觀了。（板書：形——直觀）

2.即時練習，應用規律

完成數學書第107頁的填空。

3.探究“[12+14+18+116+132=？]”

師：以形載數，能讓我們找到數的運算規律;以形載數，還能幫助我們巧妙解決比較復雜的數學問題。仔細觀察，這里的分數有什么特點？這些“數”能不能借助“形”表示出來？

（學生畫圖，教師巡視。指名匯報，輔以課件演示）

師：通過畫圖，我們得出[12+14+18+116+132]=

1-[132]=[3132]。

師：如果不結合圖形，我們用通分的辦法也能求出答案。那我們用圖形表示這個算式有什么好處呢？

生：能一眼看出答案，涂色部分就是1個整體減去空白部分。

生：從[12]開始，依次加的分數是前一次的一半，按照這個規律寫分數，用1減去式子中最后一個分數就是這個連加算式的得數，結合圖形就能理解這個算理。

評析 學生經歷從“數”及“形”到由“形”到“數”的過程，能直觀發現數與形的對應關系，結合圖形與算式，發現計算規律，并應用規律解決同類計算問題。教師讓學生初步體會“形”能直觀解釋“數”，以形助數，見數思形，通過數與形的對應關系，互相印證結果，感受數學的魅力。形的問題中包含數的規律，數的問題也可以用形來幫助解決。通過畫圖巧算結果，學生感受數形結合的優點，逐步養成數形結合的習慣，提高數形轉化能力和數學分析能力，實現形象思維和抽象思維的互助互補、相輔相成。

三、辨析感悟“形缺數時難入微”

師：華羅庚爺爺說過，數缺形時少直觀，那形缺數時又會怎樣呢？（再次播放視頻）看起來兩次都拼成同樣大的三角形，怎么在第二次的拼圖里缺了一小塊呢？（同桌合作，拼圖觀察）

1.探究三角板中兩個角的大小

師：我們先判斷黑板上畫的兩個角（如圖1），∠1和∠2哪個大？ [1][2]

生：一樣大！

師：現在光有圖形，沒有數，很難下定論。

[教師組織學生拿出拼板器具中的三角形，尋找直角邊的長度數據，并給黑板上的三角形的直角邊分別標上長度數據（2，5）（3，8）（如圖2）]

師：現在這兩個直角三角形的直角邊有了數，怎么根據這些數來判斷兩個角的大小呢？其實可以用兩條直角邊的比值來表示斜邊與直角邊的夾角的大小。

[課件出示：直角邊2格、5格的三角形，直角邊4格、10格的三角形（圖略），這兩個角大小相等嗎？為什么？]

生：[25=410]，說明這兩個銳角的大小相等。

師：把這兩條斜邊平移，就會在一條直線上（課件演示兩條斜邊在一條直線上）。

[課件出示“魔術拼板”的兩個直角三角形：直角邊2格、5格，直角邊3格、8格（如圖2）]

師（指圖2）：這兩個銳角大小相等嗎？

生：看看[25]是否等于[38]。通分得出，[25]=[1640]，[38]=[1540]，[1640]≠[1540]，所以這兩個角的大小不相等，相差一點。

師：通過數的大小比較，我們判定這兩個角大小不同，現在我們拿出這兩塊三角板操作驗證一下，重疊比較這兩個角，你們發現了什么？

生：將兩個角重疊對比，發現兩個角大小不同，兩直角三角形的斜邊不在一條直線上。

師：那剛才怎么說這兩個角一樣大呢？

生：那是因為這兩個角的大小相差太小，我們看不出來。

師：這種很細微的差別，用圖形能表示出來嗎？用什么才能精確表示出來？

生：數。

師：所以華羅庚爺爺說過，形缺數時難入微。很細微的差別，有圖形而沒有數，不能區分表示。（板書：數——精準）

2.探究拼圖中空白小正方形的由來

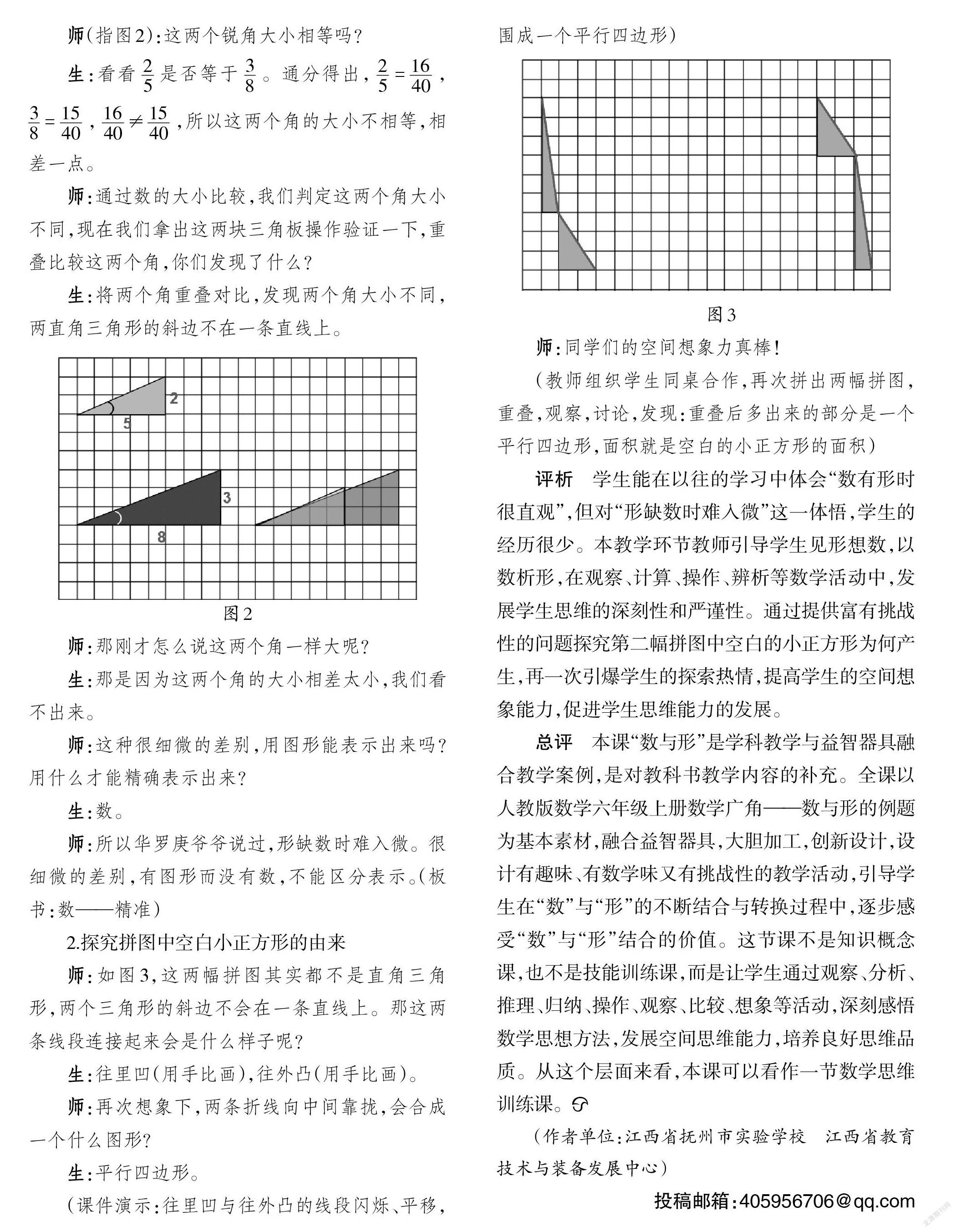
師：如圖3，這兩幅拼圖其實都不是直角三角形，兩個三角形的斜邊不會在一條直線上。那這兩條線段連接起來會是什么樣子呢？

生：往里凹（用手比畫），往外凸（用手比畫）。

師：再次想象下，兩條折線向中間靠攏，會合成一個什么圖形？

生：平行四邊形。

（課件演示：往里凹與往外凸的線段閃爍、平移，圍成一個平行四邊形）

師：同學們的空間想象力真棒！

（教師組織學生同桌合作，再次拼出兩幅拼圖，重疊，觀察，討論，發現：重疊后多出來的部分是一個平行四邊形，面積就是空白的小正方形的面積）

評析 學生能在以往的學習中體會“數有形時很直觀”，但對“形缺數時難入微”這一體悟，學生的經歷很少。本教學環節教師引導學生見形想數，以數析形，在觀察、計算、操作、辨析等數學活動中，發展學生思維的深刻性和嚴謹性。通過提供富有挑戰性的問題探究第二幅拼圖中空白的小正方形為何產生，再一次引爆學生的探索熱情，提高學生的空間想象能力，促進學生思維能力的發展。

總評 本課“數與形”是學科教學與益智器具融合教學案例，是對教科書教學內容的補充。全課以人教版數學六年級上冊數學廣角——數與形的例題為基本素材，融合益智器具，大膽加工，創新設計，設計有趣味、有數學味又有挑戰性的教學活動，引導學生在“數”與“形”的不斷結合與轉換過程中，逐步感受“數”與“形”結合的價值。這節課不是知識概念課，也不是技能訓練課，而是讓學生通過觀察、分析、推理、歸納、操作、觀察、比較、想象等活動，深刻感悟數學思想方法，發展空間思維能力，培養良好思維品質。從這個層面來看，本課可以看作一節數學思維訓練課。

（作者單位：江西省撫州市實驗學校 江西省教育技術與裝備發展中心）

投稿郵箱：405956706@qq.com