于“變”中尋其“宗”

白楊 翟秀蕊

摘? 要：針對“圖形的變化”領域的試題，根據2021年部分省、市中考數學試卷中的典型題目，總結出五個方面的特點，即重視基本性質、貼近實際生活、抓住不變本質、考查探究能力、培養全面思維，并逐一進行例題的解答和分析說明. 對解題方法進行提煉總結后，得到的解題經驗是：回歸教材基礎、剖析基本性質、查看前題提示、類比解題方法、關注核心元素、探究變化規律.

關鍵詞：典型例題;解法分析;基本模型;回歸教材

《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）指出，“圖形的變化”是一類以圖形為教學和考查的載體，以引導學生領悟變化過程中的不變量為主要目的的學習活動. 命題專家在設計“圖形的變化”的題目時，一般是從“圖形變化的方式”入手，結合平時的動手操作、構建基本圖形，注重尋找題目中圖形變化的本質，從而解決問題. 近年來，“圖形的變化”領域的試題形式較為穩定，但試題命制者仍在根據最新教育理念和改革風向不斷探索和創新，以便更好地達到課程設置的要求和目標.

一、試題分析

從2021年各省、市中考數學試題來看，“圖形的變化”領域的試題一般以問題串的形式出現，難度層層遞進，題目注重體現基本圖形的性質和判定的應用，注重學生的閱讀和動手操作能力，注重數學的實際應用，注重知識點的遷移創新，考查學生獨立面對全新數學問題的探究能力，為學生更高階段自主學習鋪路.

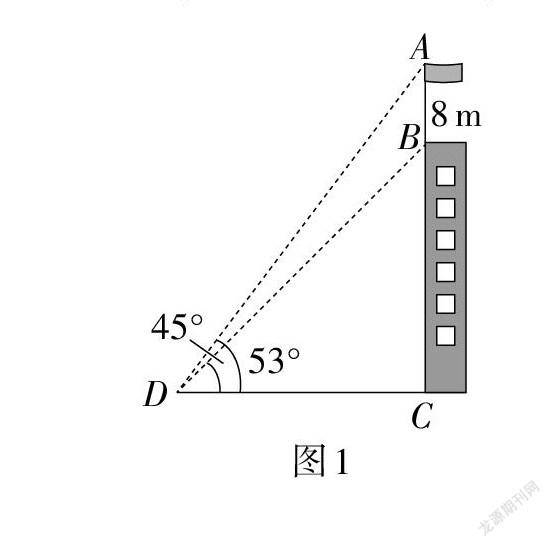
通過題中數據列方程就可以求得建筑物高.

【評析】此題主要考查三角函數和一元一次方程，題目以測量建筑物高為背景呈現，體現了數學的實用性，解題的關鍵是尋找兩個直角三角形的公共邊，并用公共邊表示其他未知量，最后通過方程即可求解.

3. 透過變化因素，抓住不變本質

例3 （浙江·嘉興卷）小王在學習浙教版九年級上冊教材第72頁例2后，進一步開展探究活動：將一個矩形ABCD繞點A順時針旋轉α（0° < α ≤ 90°），得到矩形AB′C′D′，連接BD.

（3）在第（2）小題的基礎上繼續探究圖形中線段之間的關系，如圖3（2），通過連接AM可得△AMD′與△AMD全等. 進而得到∠NMA與∠NAM之間的相等關系，實現了線段AN與MN之間的轉化，最后通過△NPA與△NAD相似得到題中三條線段的關系.

【評析】試題考查了三角形角之間的關系、矩形的性質、全等三角形、相似三角形的判定和應用. 以矩形旋轉的位置變化這一動態過程為線索，結合教材的基礎知識考查學生獨立思考，活學活用教材知識，發現、分析、解決問題的能力.例如，第（1）小題中，抓住旋轉之后三點共線，再結合旋轉過程中保持不變的幾何量——角，于是得到相似三角形. 第（2）小題表面上與第（1）小題有差異，但本質還是用了旋轉之后長度、角度不變，通過平行線轉換角，找到全等三角形. 第（3）小題在第（2）小題的基礎上繼續探究圖形中三條線段之間的關系，三條線段之間的關系通常有兩短線段的和等于最長線段、兩短線段的平方和等于最長線段的平方、中間線段是最長與最短線段的比例中項等. 先說第一種關系，則需要證明DM = PN，也就是證明△ADM ≌ △NAP，根據對應關系，會發現這兩個三角形全等后得到的是AP = DM，并不是DM = PN;再說第二種關系，觀察圖形可以發現以最長線段DN為斜邊的直角三角形旋轉前后都不存在;最后是第三種關系，結合圖形，通過觀察可以發現這三條線段在同一條直線上，需要轉化為非共線關系，觀察圖形可以發現MN與AN看起來差不多相等，所以結合第（2）小題中角之間的關系可證MN = AN，最后通過母子型△NPA與△NAD相似就得到題中三條線段的關系了.

【評析】這道題將這四條線段順次首尾相接.把其中一條固定，讓其他線段隨著其中一條線段的旋轉而運動，當線段旋轉到不同的位置時，研究線段和角之間的關系. 這類試題的難點主要在于當線段旋轉到既定位置時，需先確定其他線段的位置，進而根據已知條件求解. 例如，“發現”這一問題，需要學生先畫出當旋轉角α為60°時，其余相關線段的位置，而這就要求教師在平時的教學中先制作教具進行演示，提升學生的空間想象能力. 要求學生動手把圖形的動態旋轉圖形畫出來，就是圖形每旋轉一個小的角度都要按照線段之間的關系畫出圖形，觀察是否符合題意，從而得到正確的圖形. 經過不斷的訓練和積累，圖形在學生眼里就會運動起來，學生的空間想象能力就逐漸建立起來了，積累了畫圖經驗，對此類問題就可以應付自如了.

這類題目能夠初步考查學生獨立面對全新數學問題的探究能力，為學生更高階段的自主學習鋪路，為學生終身發展服務，在2021年各省、市中考數學試題中得到了應有的重視.

分別計算，即可解得點D的坐標.

【評析】此題主要考查了二次函數的圖象與性質、勾股定理及其逆定理、直角三角形斜邊中線定理等相關知識，以及相似三角形的判定與性質，綜合性較強，試題注重線段長度與點坐標的融合，彰顯了用代數方法解幾何問題的優勢. 學生在解題時要注意利用坐標計算線段的長度，可以起到事半功倍的效果. 例如，第（2）小題第①問可以設D，E兩點的橫坐標，代入函數表達式得到DE，DF的長度，進而得到二次函數表達式，求得最大值. 第（2）小題第②問以點G是AC的中點為切入點，利用直角三角形斜邊中線是斜邊的一半，認識到相似中的原始三角形AOG是等腰三角形，所以以點C，D，E為頂點的三角形也是等腰三角形，從而打開解題突破口.

二、解法分析

求解“圖形的變化”領域的試題時關鍵要把握三點：一是回歸教材基礎，剖析基本性質，在復雜的圖形變化中辨識對應教材中的知識考查要點，回憶教材上的基本性質，再根據題中條件求解;二是查看前題提示，類比解題方法，關注漸次遞進問題的基本解題思路，進行數學方法的類比遷移，從而根據前題解后題;三是關注核心元素，探究變化規律，抓住問題產生過程中的不變本質，關注圖形平移、旋轉、對稱中的變與不變，回憶學過的特殊條件下的解題思路，補充必要的全等三角形或相等角求解.

1. 回歸教材基礎，剖析基本性質

例6 （四川·成都卷）如圖7，在矩形ABCD中，AB = 4，AD = 8，點E，F分別在邊AD，BC上，且AE = 3，按以下步驟操作：

第一步，沿直線EF翻折，點A的對應點A′恰好落在對角線AC上，點B的對應點為點B′，則線段BF的長為__________;

第二步，分別在EF，A′B′上取點M，N，沿直線MN繼續翻折，使點F與點E重合，則線段MN的長為__________.

解析：此題以軸對稱為背景，所以應從軸對稱的性質入手，逐一對照性質找到解題突破口，軸對稱的性質3是對應點連線被對稱軸垂直平分，通過作垂線構造相似三角形，如圖8（1）所示. 由△FEG ∽ △ACD，可得[FGEG=ADCD]，易得BF的長度. 繼續翻折，依然是從軸對稱的性質入手，由對應點連線被對稱軸垂直平分，得MN⊥EF，MN∥AC. 求MN，需再次作垂線構造直角三角形，作MH⊥A′B′，如圖8（2）所示. 利用梯形中位線性質，得MH = 2. 再由△MNH ∽ △ACD，即可求得MN的長度.

三、試題解法賞析

作為中考壓軸題之一的“圖形的變化”模塊解答題，命題者在設計條件之初就給足了學生思考的空間，為學生多法求解留下充足余地. 一道好題可以從不同角度、按不同思路、用不同方法給出解答，經常思考多種解法可以培養學生的創新思維，幫助學生積累解題經驗，豐富解題思路，不斷提升其解題能力.因而，一線教師在日常教學中要多引導、鼓勵學生思考一道習題的多種解法，這是提升學生能力的重要教學方法. 以下是一例優秀試題的多種解答，供大家參考.

例9 （山西卷）問題情境：數學活動課上，老師出示了一個問題：如圖14（1），在?ABCD中，BE⊥AD，垂足為點E，F為CD的中點，連接EF，BF，試猜想EF與BF的數量關系，并加以證明.

獨立思考：（1）試解答老師提出的問題;

實踐探究：（2）希望小組受此問題的啟發，將?ABCD沿著BF（F為CD的中點）所在直線折疊，如圖14（2）所示. 點C的對應點為點C′，連接DC′并延長，交AB于點G，試判斷AG與BG的數量關系，并加以證明.

問題解決：（3）智慧小組突發奇想，將?ABCD沿過點B的直線折疊，如圖14（3）所示. 點A的對應點為點A′，使A′B⊥CD于點H，折痕交AD于點M，連接A′M，交CD于點N. 該小組提出一個問題：若此?ABCD的面積為20，邊長AB = 5，BC =[25]，求圖中陰影部分（四邊形BHNM）的面積.試思考此問題，直接寫出結果.

【賞析】此題是以平行四邊形為背景的綜合題，考查了平行四邊形的判定和性質、軸對稱的性質、直角三角形的性質和判定、等腰三角形的性質和判定、全等三角形的性質和判定、相似三角形的性質和判定等知識，要求學生能夠熟練掌握從復雜題目中提煉知識點，并靈活運用常見的解決方法逐個擊破，綜合解決問題.題目給出的條件較為寬泛，因而此題的解題思路眾多，學生觀察圖形變化的角度和對題干條件分析的側重點不同，解法也就五花八門，這些方法大都來自復習過程中常見的解題策略. 其中，根據圖形合理猜想，從問題本身入手思考是十分便捷的解法，教師可以引導學生在遇到難題時多多思考和運用. 另外，在備考過程中重視一題多解有利于發散思維，應對考場上出現的新題、難題，往往可以事半功倍，教師也應定期組織，在課堂上安排學生自主思考多樣的解法.

綜上，2021年各地中考數學試卷中“圖形的變化”領域的試題有著基礎性、應用性、創新性等特點，在考查基礎、方法、經驗和能力上大做文章，狠下功夫，全面貫徹落實《標準》中要求教師回歸教材、重視基礎的同時提升學生綜合素養和創新能力的基本理念. 今后，在“圖形的變化”領域，優秀的試題不僅要求學生有更扎實的基本功，對各類性質有更高的熟悉度，還將進一步加大數學應用的比例，即對學生綜合處理信息、排除無用條件、快速篩查有用條件的能力要求更高. 更加有利于學生提高能力、提升素養、增長經驗，有利于學生的長期發展. 對學生的更高要求意味著一線教學需要教師具備更高的教學水平，今后教師在注重“四基”和“四能”教學的基礎上，一定要嚴格落實“圖形的變化”領域的教學要求，落實《標準》的理念和評價要求，更多地鞏固教材基礎，傳承數學文化，實現數學價值，厚植數學情懷，以中考數學試題中“圖形的變化”的內容為載體，緊跟數學教學改革大潮，為未來的數學教學帶來充滿生機和活力的新局面.

參考文獻：

[1]中華人民共和國教育部制定. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.

[2]全國中小學教師繼續教育網. 2011年版義務教育課程標準解讀（初中數學）[M]. 北京：中國輕工業出版社，2012.

[3]孟學明，郭福生. 把握圖形變化本質，追根溯源考查方向：2019年中考“圖形的變化”專題解題分析[J]. 中國數學教育（初中版），2020（1 / 2）：97-103.

[4]孫玉軍，宋先波，劉忠. 2018年中考“圖形的變化”專題解題分析[J]. 中國數學教育（初中版），2019（1 / 2）：91-98.