含有執行器失效的風力發電系統的切換控制
王宏偉,張 倩
(1.新疆大學電氣工程學院,新疆 烏魯木齊 830047;2.大連理工大學控制科學與工程學院,遼寧 大連116024)
1 引言
風力發電屬于分布式發電系統當中的重要構成部分之一,作為清潔能源當中的典型代表,此種能源的利用不需要付出環境的代價,可以有效規避對環境所造成的污染。當前不少歐洲國家都在大力推廣風電,我國也都在適合建設風力發電的區域內大量建設風電場基地。風力發電一般包含控制系統、感應發電機和傳動裝置等,以及其它附屬設備。風力發電機在整個系統當中的作用就是轉化風的動能,再轉化為機械能之后再轉變為電能。圖1為雙饋式風電機組的示意圖[1,2]。

圖1 雙饋式風電機組的示意圖
在雙饋式風電機組發電系統中,由于系統轉動慣量、風機葉片質量、永磁體的磁化強度等系統本身參數的變化[3],以及元器件的老化、亞健康或非正常工作等因素的影響,用原先的控制算法可能會導致老化的系統性能出現不穩定。同時,系統的內部變化會發生失速、轉動軸嚴重破壞等故障,影響到整個系統的安全運行。大多數情況下,一些執行器的老化和故障通過人為診斷或者智能自動診斷可以盡快排除,從而使系統盡快工作。例如風電系統液壓/氣壓泄露、電路電阻增加或者電源電壓下降等故障,通過計算機的大數據分析、機器學習等方法對執行器故障進行自動檢測、隔離、辨識,并使失效的執行器恢復健康,該類系統簡稱為執行器失效的系統。在執行器有故障或者失效時,系統處于開環狀態,其穩定性難以保證。因此,對于執行器失效風力發電系統的控制研究,對于風電系統有著非常重要的理論和實踐意義。
對于風力發電系統的控制,很多學者提出了很多控制方法,例如最優控制[4]、滑模變結構控制[5]、神經網絡PID[6]、非線性自適應控制[7]等。文獻[8]提出了虛擬參數的PPB控制方法,將風力發電的非線性系統精確線性化,然后設計控制器實現系統控制。可靠控制在近年來得到很多研究者的關注,提出了許多可靠控制的研究成果[9-12]。可靠控制的優點是:故障發生時,能及時地實現容錯控制,特別是采用自適應容錯控制,不需要故障診斷機構提供精確信息,利用自適應控制的原理設計自適應控制算法來在線診斷和控制[13,14]。自適應容錯控制已在重大安全系統,例如石油化工、核反應堆、飛行器、網絡控制[15-17]等系統中進行了應用。在這些自適應容錯控制方法中,如何處理非線性系統現象仍是自適應容錯控制器設計的難點問題。
對于圖1中的雙饋式風電機組的故障,很多文獻對其進行了研究。這些故障可以分為故障在線可恢復、故障離線恢復、不可恢復三類[16]。例如變槳距控制中的液壓/氣壓泄露、電路電阻增加、電源電壓下降等故障通過傳感器測量,在線診斷后就可及時修復,屬于故障在線可恢復類。本文以故障在線可恢復類的風電系統作為研究對象,在執行器健康良好期間,系統處于閉環狀態,屬于恢復正常事件;在執行器暫短失效期間,系統處于開環狀態,屬于暫時失效事件。通過“恢復開關”的“合上、斷開”使得系統在閉環和開環之間,或者在恢復正常事件和暫時失效事件之間進行切換。利用切換控制原理設計了控制器,并保證了此類閉環切換系統的穩定性;最后,對含有執行器失效的雙饋風力發電機組進行仿真驗證所提出方法的有效性。
2 含有執行器失效風力發電系統模型的建立
對于圖1所示的風電系統,可以采用如下模型進行描述
(1)
其中,x∈Rn,u∈Rm分別為系統的狀態變量、控制輸入信號;z為系統的輸出信號;A、B1、B2、C為適當維數的參數矩陣。
對于系統(1),執行器失效是指可恢復健康的一類暫時失效。在本文中,用“恢復開關”來描述執行器的工作狀態和模式:當恢復開關閉合時,表示執行器良好,記為恢復正常事件;當開關打開時,表示執行器失效不工作,記為暫時失效事件。
為了更好地說明這兩個事件,本文在切換時間上進行了標定,即兩類事件交替切換的時刻集合為Γ={t0,t1,t2,…|0≤t0 這樣,可以得到描述執行器的暫時失效和恢復健康的兩個事件模型: 暫時失效事件I (2a) 暫時失效事件II (2b) 其中,x∈Rn,u∈Rm,z∈Rl,它們分別為系統的狀態向量,控制輸入向量和輸出向量;w(t)∈L2[0,∞)為外界擾動信號;A,B1,B2,C為適當維數的參數矩陣。 如果系統含有不確定項,式(2)還可以表示成 暫時失效事件I (3a) 恢復正常事件II (3b) 其中ΔA、ΔB1為不確定項,它們滿足下式 [ΔAΔB1]=DF(t)[E1E2] (4) 其中,D、E1、E2為已知的實數矩陣,F(t)是未知的、有界的、不確定性矩陣,滿足 FT(t)F(t)≤I (5) 式中I為單位矩陣。通過式(3a)、(3b)的表達,可以看出系統是在執行器“恢復正常”、“暫時失效”離散事件驅動下交替進行切換控制。 對于系統(3),采用控制方式是:執行器良好時,加入狀態反饋控制器;在執行器出現失效時,不加控制器,即為 (6) 將上式代入(3),此時相應閉環系統為: 暫時失效事件I (7a) 恢復正常事件II (7b) 為了更好地研究,采用T0(τ,t)代表執行器失效的總時間,采用T1(τ,t)代表執行器良好的總時間,它們表示了[τ,t]內兩種狀態的總時間 T0(τ,t)+T1(τ,t)=t-τ (8) 在此,給出相關性的一些定義和引理, 定義1:若存在t、τ∈R+(R+表示正實數),t>τ,和常數λ∈(0,1),Tu>0,使得 T0(τ,t)≤λ(t-τ)+Tu (9) 成立,則稱具有不大于λ的失效率。 定義2:給定的常數γ>0,初始條件x(0)=0,對系統(3)在控制器(6)作用下,在外界干擾信號w(t)∈L2[0,∞)下,如果滿足如下控制指標 則稱系統(3)具有性能指標γ的H∞控制。 定理1:對系統(3)在控制器(6)作用下,如果存在正定矩陣P>0,以及正數λ0,λ1,γ0,使得下面不等式成立 (10) (11) λ0λ-λ1(1-λ)<0 (12) 則閉環系統(7)是指數漸近穩定,同時H∞性能指標γ滿足 (13) 證明:下面將分成不含外界擾動(w(t)=0)和含外界擾動(w≠0)兩部分來證明。 1)首先令w(t)=0,研究閉環系統(7)的穩定性。 對于(7),選取Lyapunov函數為 V(t)=xT(t)Px(t) (14) 由不等式(10)和(11)可等價于下面不等式, 可以整理得 將V(t)沿式(7)的解求導,結合上面不等式有 可以得到下面結果 (15) 在?t∈(t2k-2,t2k-1],k∈N,上式的第2式進一步整理可得 V(t)≤e-λ1(t-t2k-2)V(t2k-2) ≤e-λ1(t-t2k-2)eλ0(t2k-2-t2k-3)V(t2k-3) ≤…≤eλ0T0(0,t)-λ1T1(0,t)V(0) (16) 在?t∈(t2k-1,t2k],k∈N,式(15)的第1式進一步整理可得 V(t)≤eλ0(t-t2k-1)V(t2k-1) ≤eλ0(t-t2k-1)e-λ1(t2k-1-t2k-2)V(t2k-2) ≤…≤eλ0T0(0,t)-λ1T1(0,t)V(0) (17) 利用式(16)和式(17),就可得 V(t)≤eλ0T0(0,t)-λ1T1(0,t)V(0) (18) 利用式(8)和(9),在?t,τ∈R+,且t>τ,就有 T1(τ,t)=t-τ-T0(τ,t)≥(1-λ)(t-τ)-Tu (19) 由式(9)和(19),不等式(18)可進一步變化為 V(t)≤eλ0λt+λ0Tu-λ1(1-λ)t+λ1TuV(0) =e(λ0+λ1)Tu+(λ0λ-λ1(1-λ))tV(0) 根據式(14),就有 其中,α=e(λ0+λ1)Tu。根據不等式(12)和上式,綜上可知系統(7)指數漸近穩定。 2)含外界擾動w(t)≠0。將式(13)的V(t)沿式(7)的解求導,并利用式(10)和(11)可知 (20) ≤[V(t2k-3)eλ0(t2k-2-t2k-3)- (21) 在?t∈(t2k-1,t2k],k∈N,對式(20)的第1個式子等式兩邊取積分,可遞推得 ≤[V(t2k-2)e-λ1(t2k-1-t2k-2) (22) 式(21)和(22)都成立,即對?t∈R+,都有 (23) 由于V(t)非負性,由式(23)可得出 (24) 那么,對于任意?t∈R+,就有 由于zT(τ)z(τ)和wT(τ)w(τ)都大于等于零,利用(9)和(19),可以得到 將上式兩邊同時對t在[0,∞]內積分,即有 那么就有 由于初始值x(0)=0,上式可整理為, 根據定義2和式(13),上述不等式意味著, 即系統(3)具有H∞性能指標γ。綜合(1)和(2)的討論結果,定理1得證,證畢。 在定理1的基礎上,應用定理2給出控制器的具體設計。 定理2:設執行器最大失效率為λ,對于系統(3),如果存在矩陣W,以及正數0,1,ρ,β,ε0,ε1使得下面不等式成立, (25) (26) 0λ<1(1-λ) (27) 其中,M,滿足 M=β(A+AT)-0I+ε0DDT 證明:不等式(10)可以寫成 根據文獻[18]關于不等式引理,上式可等價于存在常數ε0>0,使得 由文獻[18]Schur補引理,上式等價為下列不等式矩陣 將上式左邊分別左乘和右乘diag{P-1,I,I,I},令X=P-1,可得 同樣,不等式(11)可以寫成, +(E1+E2K)TFT(t)(PD)T 根據文獻[18]關于不等式引理,上式可等價于存在常數ε1>0,使得下列不等式成立 由文獻[18]的Schur補引理,上式等價為 將上式左邊分別左乘和右乘diag{P-1,I,I,I},令X=P-1,可得 考慮如下雙饋風力發電變槳系統的控制問題,其動態模型如下[12]: (28) 定義 矩陣F中參數范圍是:-1≤r1≤1,-1≤r2≤1,-1≤s1≤1 則式(28)可以寫為 假定采樣周期T=1s,仿真時間為500s。系統的執行器在[10s,25s]、[50s,60s]、[100s,125s]時間段失效,其余時間正常。風電變槳系統執行器正常工作總時間450s,工作率為90%,失效總時間50s,失效率為10%。 通過定理2可得,β=0.85,λ0=0.5618,λ1=0.8985,ρ=0.5423,γ=0.7364。此時矩陣W為 則反饋控制器為 圖2給出了風力發電槳距角四個狀態變量變化過程;圖3給出了控制器的變化。 圖2 狀態變量的動態變化 圖3 控制器的變化 通過觀察圖2和圖3可以得到以下幾個結論: 1)在系統的故障可以自診斷和自修復的情況下,所設計的控制器可以完成執行器臨時失效的系統控制,該方法簡單易行。 2)即使系統多次出現執行失效和參數的不確定性,只要是失效的駐留時間不是很長,在系統不確定參數有界的情況下,所設計的控制器能夠保證系統穩定運行。 針對含有執行器失效可恢復的風力發電系統,采用恢復開關的“導通”和“斷開”來描述執行器良好和故障兩種工作狀態,引入切換控制理論實現其控制。對含有執行器失效和不確定性外部干擾的系統,基于穩定性理論給出了魯棒控制器的設計。對于含有集群風電系統的故障容錯控制是很難解決的問題,今后在這方面給予關注。3 含有執行器失效系統的控制器設計

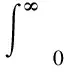
















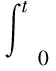
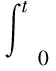




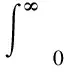




4 仿真實例



5 結論

