倉儲密集區域物流配送點儲位分配優化仿真

付 芳，周萬洋

(1.江西應用科技學院，江西 南昌 330100；2.德拉薩大學達斯馬瑞納校區，菲律賓 卡威迪省)

1 引言

隨著電子商務發展進程的加快，對于倉儲管理能力和物流儲位分配能力的要求也在不斷提高。物流企業中最關鍵的環節即為儲位分配和出入庫效率。尤其是在倉儲密集區域，為使有限的空間發揮最大的利用價值，需要對產品入庫、存儲以及出庫進行不斷地優化。

目前，大多數企業在存儲貨物時，仍采用傳統的高低貨架的形式，對于規模較小、發貨量較低的企業來說是可行的，但是對于倉儲密集區域來說，限制了貨物的出庫效率。為使出庫效率滿足企業發展的需求，對有限的儲位進行分配優化是非常有必要的。作為現代物流倉儲系統中最先進的技術，自動化立體倉儲系統在各行各業都起到了非常巨大的作用。但是從現有的研究成果中發現，部分應用了自動化立體倉儲系統的企業面臨以下幾點難題：對貨物儲位分配[1]不合理；貨物擺放高度不確定；貨物出入庫效率低，各個環節之間缺少協同工作。

針對現階段存在的問題，本文提出了一種新的儲位分配優化方法。分析儲位分配應遵循的原則，在此基礎上對倉庫內所有的儲位進行編碼排序，以便計算其與出入庫站臺之間的距離，將需求量較大的貨物存放在最近的地方。通過遺傳算法對多目標函數求得最優解，所得結果即為優化后的儲位信息。通過搭建仿真平臺，在真實的企業中參考各項參數，最終設計實驗驗證了本文方法在保證貨架穩定性以及出入庫效率的同時，實現合理的儲位分配。

2 儲位分配方式和分配原則

2.1 儲位分配方式

針對大小不同、類型不同的倉庫，貨物儲位的分配方式也有所不同，常見的貨物儲位的分配方式有三種：分類存儲、指定存儲和隨機存儲。三種存儲方式各有優缺點，利用指定存儲舉例說明：某企業將生產物料按照不同的類型和使用范圍將倉庫[2]劃分為不同的區域，指定區域只允許擺放相對應的貨物。這種方式一般情況下都需要人工揀選，效率較低，而且對倉庫的存儲空間來說也是一種很大的浪費。

對于企業生產物料的分類方法比較常用的就是ABC分類法。該方法按照物料的經濟價值和使用價值進行分類，將重要物料和一般物料區分開，采取不同的存儲方式。這種方法通常將物料分為A、B、C三類，A類為價值最高的物料，重要程度為最重要，主要特征值可達到70%～80%。B類為一般物料，主要特征值在10%～20%之間，其余的為C類物料，重要程度為最不重要。ABC分類法可實現對物料的有效分類，但是對于儲位的分配效果并不理想。

本文將以上ABC分類法與物料清單(Bill of Material，BOM)結合在一起，充分利用ABC分類法的有效分類，與BOM工藝表整體規劃[3]相結合，實現儲位的合理分配，提高貨物的入庫效率和出庫實時性。

2.2 儲位分配原則

貨物在倉儲儲位中的分配應遵循以下原則：

1)在分配貨物儲位時，要充分考慮到出入庫的時間，選擇最短路徑；

2)對于多巷道倉庫，貨物盡可能分散存儲，避免因一條巷道的擁堵影響該區域內貨物的出入庫；

3)相同貨物在出入庫時要充分遵循“先進先出”原則，避免貨物因長期積壓出現過期、損壞等情況；

4)貨物的擺放要遵循“下重上輕”原則[4]，重量較大的貨物擺放在貨架底部，較輕的則擺放在貨架頂部，避免貨架出現受力不均，倒塌的情況。

3 儲位分配優化

3.1 儲位編碼

按照“1～最大儲位數”的規律對倉庫中的所有儲位進行編碼排序，號碼信息代表了貨物所在的位置。根據貨物所在的排、列、層，如第3排第4列第2層的貨物位置編碼為03×04×02。

編碼完成后，再計算貨物所在的位置與出入庫站臺之間的距離特征碼。考慮到倉庫的出入庫為同一站臺的情況，在進行儲位編碼[5]時，通過儲位所在的位置與出入庫站臺之間的距離來確定。

儲位位置信息與出入庫站臺之間的距離特征碼表示為

(1)

其中，Dist(z)表示貨物所在儲位與出入庫站臺的距離特征碼，z=1，2；a為一個常數項，結果為堆垛機在水平方向與垂直方向上，經過儲位所用時間之比。a的值為

a=vyL/(vx-H儲位)

(2)

其中，vy表示堆垛機在垂直方向上的行進速度；vx表示堆垛機在水平方向上的行進速度；L為每個儲位的長度單位；H儲位為每個儲位的高度單位。

例如，假設某物流企業的堆垛機在水平方向上的行進速度為120米/分鐘，在垂直方向上的行進速度[6]為30米/分鐘，儲位的長度為1.45米、高度為0.8米，那么可得a=0.45。假設該企業的倉儲貨架為p行q列，將出入庫站臺所在的位置看作為0，距離站臺最近的貨物為第1列第1層。代入式(1)，即可得到第2排第5列第5層的距離特征碼為

Dist(1)=max(0.45×|5-0|，|5-2|)=2.25

(3)

按照上述方法，將需求量較大的貨物盡可能存放在離站臺近的貨架上，使堆垛機的揀選路徑最短，效率最高。

3.2 儲位分配數學建模

對儲位編碼后，計算與出入庫站臺之間的距離，可選擇最短路徑存取貨物。接下來，要劃分倉庫內貨架的擺放區域，完成劃分后根據貨物的具體使用范圍和類型再優化儲位的分配。假設已知貨物自身需求量、出入庫數量、使用范圍和貨物類型以及單個貨物的重量。

將貨架按照層數分為不同的扇形區域，假設貨架有2層，即劃分為2個扇形區域，根據貨架上貨物的需求量以及重量建立多目標函數。將貨物分為u種不同的類型，w表示貨物自身重量與出入庫頻率之間的權重值，w={0，1，2，…，u}。根據w的大小對倉庫內貨架進行分區。表1為在同一區域內，與w值相同的貨物擺放的位置，隨著w值的變化，距離出入庫站臺的距離也在不斷發生變化，w值越小，說明離站臺距離越近，反之，則越遠。

表1 8列4層的貨架4分區扇形分區

根據上述對貨架區域的劃分，若某一區域內出現貨架無法滿足貨物存放需求的情況，則按照就近原則[7]，用與之相鄰的貨架進行貨物的存取。

完成對貨架區域的劃分后，即可對貨物儲位進行分配。首先，根據貨架分區原則，將貨物進行合理的存放；然后通過儲位優化策略對區域內的儲位進行管理和優化。

儲位分配數學建模過程如下：對于一個p行q列的貨架來說，將i列j層的儲位坐標記為(i，j)(i=1，2，…，p；j=1，2，…，q)，出入庫站臺記為(0，0)，將貨物自身的重量以及出入庫的頻率作為影響貨架儲位分配的權重因素，那么可構建多目標函數如下所示

(4)

(5)

(6)

其中，S表示貨物入庫過程中所需要的總做功；T表示貨物出庫所花費的時間；xij為一個常數項，xij=0或1；mij表示i列j層貨物的重量；nij表示倉庫內所有存放貨物總數量。式(4)表示當存放了一定重量的貨物時，所做的功最少；式(5)表示當倉庫內存放了一定數量的貨物時，堆垛機揀選時間最少；式(6)表示在忽略堆垛機加速度的前提下，i列j層上的貨物從開始揀選到出庫成功所花費的時間。

3.3 儲位分配優化算法實現

在進行儲位分配優化時，最重要的參考依據為貨架的穩定性以及貨物的出入庫效率，這屬于多目標函數問題，比較常用的方法就是遺傳算法。通過選擇算子、對算子進行交叉和變異操作，最終得到多目標函數的最優解。

3.3.1 選擇算子

式(4)中對于兩個目標函數的求解過程都是求其最小值，需要將其轉換為適應值，如式(7)、式(8)所示

(7)

(8)

式中，Smax、Tmax分別表示兩個目標函數所得結果的最大值。為降低計算過程中的誤差，本文使用了余數隨機選擇策略。適應度計算的優勢是：當繁育了新一代的生物群體后，每個生物個體都含有“S”或“T”標簽，標識該個體是通過穩定性和出入庫效率計算得到的。

3.3.2 交叉算子

完成算子的選擇后，對算子進行交叉操作，組合得到新的生物個體，在空間中進行遍歷[8]，有效降低算法被破壞的概率。基于此，本文引入部分匹配交叉策略，為了某個生物個體形成單方面最優的情況，使得所有目標函數之間的優異基因可分配給多個生物個體，從而得到更優的生物個體。將這種思想應用到儲位分配中，儲位的分配優化也可看作是對貨物擺放順序的優化，將目標函數的計算結果直接應用到貨物的擺放順序中。由于儲位編碼不能出現重復的情況，所以在編碼時，根據序位號進行編碼，將不同的部位剔除掉，并打亂重新排序，得到一組新的序位號，并與未重排之前的順序進行比較，找出重疊的部分進行重新組合，即可得到交叉操作后的儲位編碼信息[9]。假設有兩個生物個體S2、T2S2=[1，2，4]，T2=[2，5，6]，在進行交叉操作時，找出二者相同的部位2，將其余不同的部分結合在一起，[1，4，5，6]，將其順序打亂重新排列，得到[1，6，4，5]，然后將其分為兩個部分，再加上相同部分2，得到新的S2′和T2′，S2′=[1，2，6]，T2′=[2，4，5]，完成交叉操作。

3.3.3 變異算子

與交叉操作相同，在進行變異操作時，同樣不能出現相同的編碼。隨機選取n個編碼，然后再選取n個編碼，將先選取的n個編碼用后選取的n個編碼做替換，確保每個編碼具有獨特的各異性。在本文中，變異操作的實質為隨機變換不同儲位上的貨物位置，在倉庫這個有限的空間內完成對貨物的位置信息變異，屬于小范圍變異[10]。

在上文建立的數學模型中，假設存在個體X2=[2，4，5]，從中任意選取一個數值作為變異算子，即對j的變異算子進行計算。

將貨架上空的儲位或者貨物被取走的儲位標記為0，按照貨架穩定性和最大存取效率原則，這些空位應被放在貨架的上方、或者離出入庫站臺最遠的儲位上，所以在進行變異操作過程中，應對貨架矩陣及時修補，將空的儲位置于貨架的最上方。

為確保變異操作所得結果為最優，在完成變異操作后還需添加適當的隨機解到生物群體中，直到找出最優解算法終止運算。一般情況下，出現以下兩種情況視為算法終止：

1)當迭代次數達到最大值時停止運算；

2)對每次計算所得結果進行穩定性測試，判斷其是否為最穩定值。在連續出現多次迭代計算結果沒有變化時，由于經過多次迭代計算，生物種群中個體的字符相似度較高，所以即使沒有得到理想的結果也要終止運算。

本文對于終止條件的選擇為如果生物群體中出現一個大于標準偏差的值，則認為當前種群的收斂程度較高，即可終止運算。對于生物群體標準偏差的計算如式(9)所示

(9)

4 仿真分析

在某物流倉儲企業進行仿真驗證，仿真平臺在CPU為IntelCorei7-8565U、PⅢ以上微機環境、系統內存大小為8GB的計算機系統上實現。

該企業倉庫中共有200個貨物，按照類型不同將其劃分為5類：1類(60個)、2類(20個)、3類(60個)、4類(20個)、5類(40個)。自動化立體倉庫設備的參數為：堆垛機在水平方向上的行進速度為180米/分鐘，在垂直方向上的行進速度為60米/分鐘，貨架儲位高度為1米，長度為1.3米。該貨架共有12層40列，按照儲位編號1，2，3，4，5劃分為5個區域，每個區域的貨物參數如表2所示。

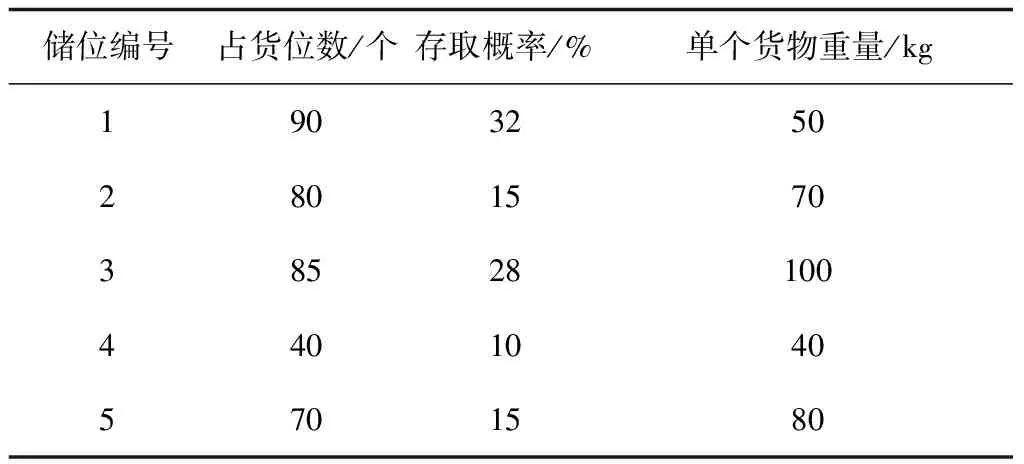
表2 貨物參數

通過求解w值計算每類貨物所在的貨架位置信息，計算所得結果為：A區所對應的貨物類型為3，B區所對應的貨物類型為1，C區所對應的貨物類型為5，D區所對應的貨物類型為2，E區所對應的貨物類型為4。區域劃分結果如圖1所示。

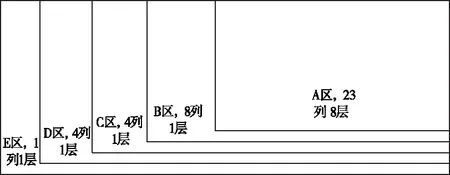
圖1 貨區分布圖

通過計算多目標函數式(4)、式(5)、式(6)的值，為200個貨物分配最佳的儲位位置，如表3所示。矩陣中數字1，2，3，4，5分別對應貨區A、B、C、D、E，這5個數字表示儲位有貨，0表示空閑儲位。同時，數字在矩陣中的位置表示該貨物在貨架上的位置。

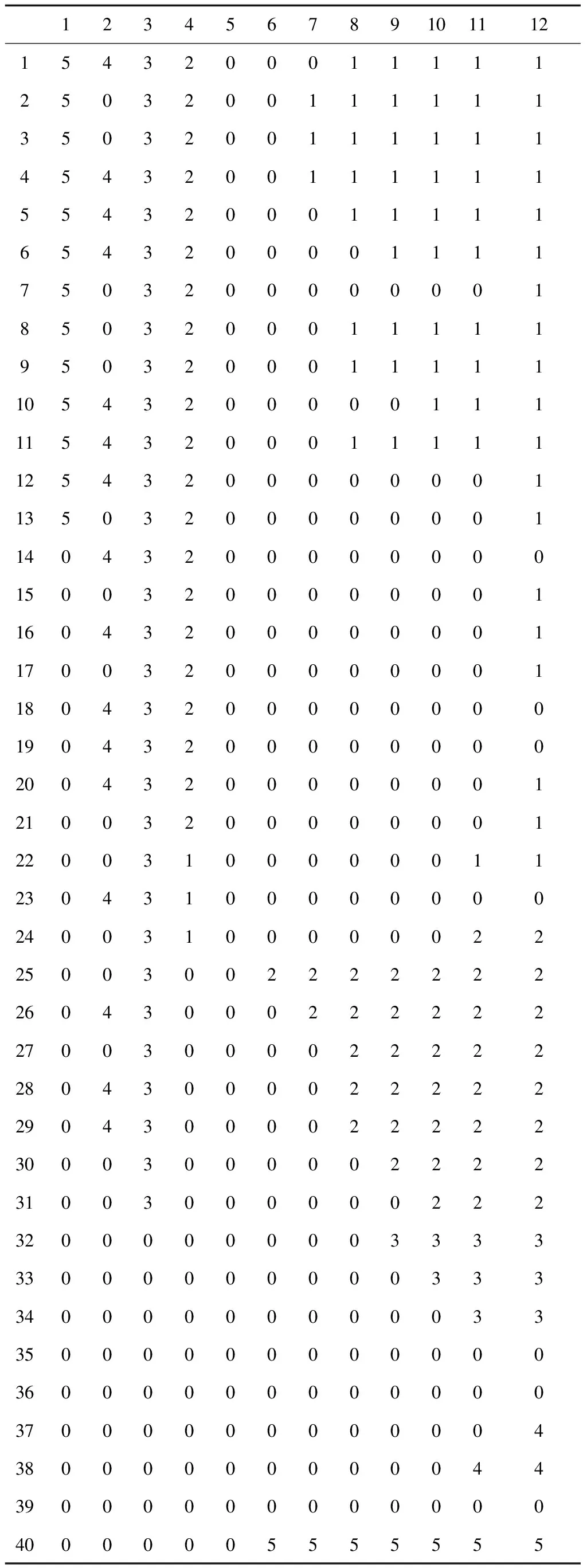
表3 200個貨物儲位分配優化表

將表3完成儲位分配優化后的位置信息代入到本文方法中，重心函數和時間函數的變化情況如圖2、圖3所示。重心函數和時間函數的數值越大，說明出入庫效率越低，即方法應用效果越差。反之，重心函數和時間函數的數值越小，說明出入庫效率越高，即方法應用效果越好。

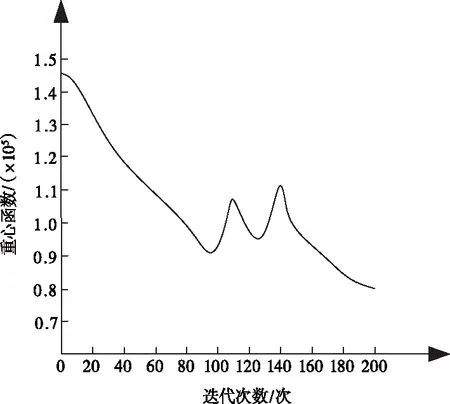
圖2 優化分配后重心函數值變化曲線

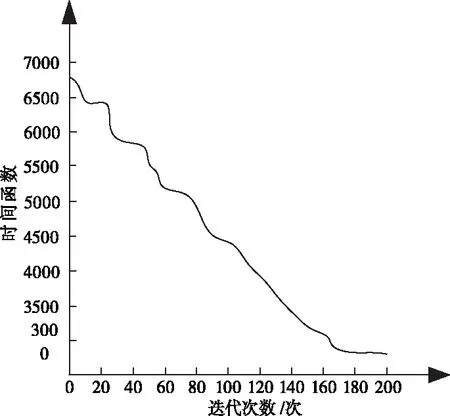
圖3 優化分配后時間函數值變化曲線

從圖2、圖3中可以看出，不管是重心函數值還是時間函數值，二者都出現了明顯的下降趨勢，當迭代次數達到貨物數量200個時，重心函數值由原來的1.45×105下降到7.49×104，時間函數值由一開始的6800下降到2700。由此可以看出，運用本文方法對貨物儲位進行優化分配后，貨物的出入庫效率和貨架重心問題都得到了優化。

5 結論

對于當前物流企業面臨的貨物出入庫效率低、無法滿足實際需求的情況，本文提出了倉儲密集區域物流配送點儲位分配優化方法。通過計算倉庫內貨架與出入庫站臺之間的距離特征碼，將重要程度較高、需求量較大的貨物擺放在離站臺最近的位置，然后利用遺傳算法對儲位優化這一多目標函數進行求解，通過選擇、交叉和變異三個操作后，得到最優解，所得結果同時兼顧了貨架的穩定性以及貨物的出入庫效率。本文方法實現簡單，計算過程中沒有添加過多的參數值，可為物流倉儲企業提供可靠的參考。