基于PSO 優化BiLSTM 的聯合循環電廠輸出功率預測

邵科嘉，周 玉，宋 豪，山浩強

（華北水利水電大學 電力學院，河南 鄭州 450045）

0 引言

隨著我國經濟持續穩定發展，國家相關部門相應提高了環保制度的要求標準，環保達標成為生產企業的一項重要任務。在發電行業，由于火電廠排放的污染物影響空氣質量，所以由燃氣輪機和蒸汽輪機組成的聯合循環機組逐漸興起。循環電廠因為能夠提供更加高效環保的電能，所以得到越來越廣泛的應用。與常規的燃煤發電相比，聯合循環發電的主要優點有：投入資金較少、污染小、效率高、調峰性能好、啟停快等。因此，燃氣輪機成為了世界上大多數熱電廠的原動機，并且從電廠優化設計到經濟運行的各個方面都得到學者廣泛關注[1]。

熱電聯產可使機組熱耗率降低，從而提高能源使用效率，具有良好的經濟性。在大多數電力市場中，每個發電廠都必須向調度中心提交其電力生產預測以確保發電廠能夠產生最佳輸出輸入比。通過對其高精度預測，可實現每兆瓦時電能的效益最優；同時有利于電力系統相關部門合理安排輸電網絡擴展規劃、生產調度、機組使用計劃，從而提高電力系統的經濟和社會效益。

聯合循環機組的輸出功率受溫度、壓力、相對濕度、燃料條件和電力需求等因素的影響而變化[2]，在一定程度上不利于并網機組穩定運行。使用熱力學方法進行精確的系統分析需要大量的假設[3-4]。為了消除這一障礙，通常使用機器學習方法進行分析。

國內外已經提出了多種基于統計學和機器學習的人工智能預測方法，包括前饋神經網絡、模糊神經模型、支持向量機以及多種組合模型等[5]。文獻[6]利用多種機器學習方法，通過實驗結果分析出不同參數與模型組合對循環電廠輸出功率預測產生的影響：首先，針對不同參數組合所得結果進行比較分析尋找最優子集；其次，針對各個機器學習方法的預測精度進行了較為全面的分析，并獲得預測精度最高的方法。文獻[7]中使用了自適應神經模糊推理系統預測核電站汽輪發電機的功率輸出。文獻[8]分析了影響燃氣輪機發電量的因素，為機組的優化運行與改造指出了實際性的解決方案。文獻[9]中提出了一種基于神經網絡的雙層遞階預測方法并進行了評價。目的是盡可能減少任何預測應用偏差產生的誤差。文獻[10]采用循環神經網絡組合模型在風電功率預測方向取得了較高的精度；但該網絡方法存在梯度下降和消失的問題。文獻[11]把LSTM 運用到了負荷預測并極大提高了預測精度。文獻[12]采用了PSO-LSTM 用于非時序電價信號的短期預測，利用粒子群算法優化LSTM 網絡輸入權重；然而未考慮粒子群自身的權重對全局最優解的影響。

與其他神經網絡模型類似，在BiLSTM 神經網絡模型中，部分參數如隱含層神經元個數、周期次數、學習率、批大小等依賴于經驗值驗證結果，具有較低的泛化性能。基于此，本文通過粒子群算法優化BiLSTM 獲得最優超參數，構建基于PSO-BiLSTM 的聯合循環電廠輸出功率預測模型。利用UCI 標準數據集對本方法和多種方法進行可行性對比實驗分析。結果表明，該方法多個預測指標表現優秀，能有效提高循環電廠輸出功率預測精度。

1 相關理論和方法

1.1 LSTM 神經網絡

為了解決循環神經網絡在梯度消失方面的問題，通過改進其隱含層，提出LSTM 人工神經網絡。LSTM 是一種特殊改進的遞歸神經網絡，其特點是增加了長短記憶功能，用長短期記憶神經網絡單元替代（recurrent neural network，RNN）單元。LSTM 應用在時間序列數據方向具有優異表現，適用于電廠輸出功率預測等場景[13]。

LSTM 改進RNN 隱含層的主要步驟如下。

Step 1：隱含層內增加遺忘門、輸入門和輸出門。

Step 2：在隱含層的內部增加長短期記憶神經網絡單元。

以上2 個步驟使LSTM 具有更好的長短期記憶功能。其中LSTM 的隱含層內部構造如圖1所示。

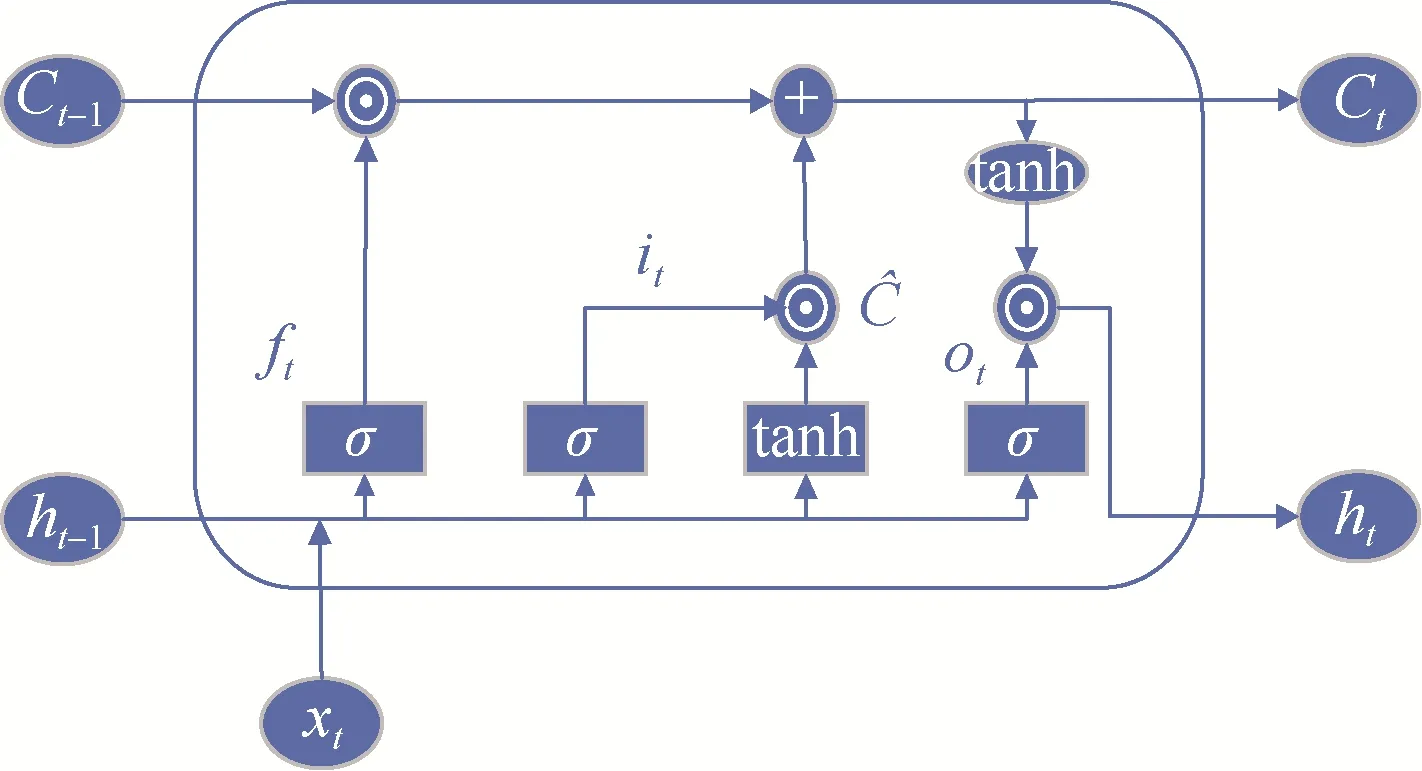
圖1 LSTM 網絡單元結構Fig.1 LSTM network unit structure

LSTM 的訓練過程如下。

（1）遺忘門層完成選擇性的遺忘部分。

式中：σ為sigmoid 函數；ht–1為上一個時間點的輸出；xt為直接輸入；Wf為遺忘門的權重；bf為遺忘門的偏置項。

（2）輸入門與長短期記憶神經網絡單元記憶過程。

式中：Wi和bi分別為函數sigmoid 在完全連接層的權重和偏移參數；WC和bC分別為全連接層tanh函數的權重和偏移參數。

（3）輸出門確定細胞狀態并將其輸出到當前時刻隱含層狀態中。

式中：ot為輸出門；Ct為當前時刻細胞狀態。LSTM網絡結構模型如圖2 所示。

圖2 LSTM 網絡結構模型Fig.2 LSTM network structure model

1.2 BiLSTM 神經網絡

電廠輸出功率數據為時序型數據。對于LSTM此類傳統單向神經網絡的預測，通常是按照時間序列從前往后進行訓練；但這種訓練形式對數據利用率較低，不能進一步挖掘數據潛在的特征[14]。

BiLSTM 神經網絡通過構造一對方向相向的LSTM 層，即在原來的基礎上增加一個反向的LSTM 層使其擁有了雙向特性[15]。雙向網絡使序列起點和終點隱含層的狀態均可進行遞歸響應訓練，能進一步挖掘當前數據與之前時刻的數據，以及和未來時刻數據之間的某種聯系，進而更深入地處理反向信息，優化長期依賴問題，提升模型的預測精度[16]。BiLSTM 網絡模型如圖3所示。

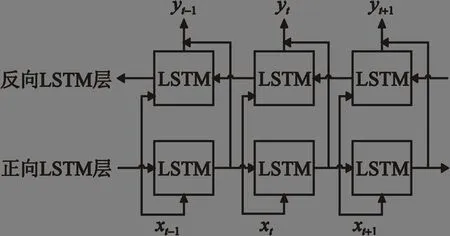
圖3 BiLSTM 網絡結構模型Fig.3 BiLSTM network structure model

BiLSTM 模型通過兩個獨立的隱藏層分析正向和反向序列，BiLSTM 預測模型中最終輸出的預測值yt由正向和反向隱含層共同決定[17]。正反向隱含層的輸出以及預測值輸出yt的計算公式如下。

正向隱含層輸出為：

1.3 粒子群算法

在實驗過程中發現，BiLSTM 關鍵超參數的選取會對預測精度產生影響，所以需對部分超參數的取值進行合理選擇。

粒子群優化算法（PSO）由模擬鳥類覓食的隨機搜索算法進行改進。相較之其他隨機搜索算法的盲目性搜索，該算法在搜索過程具有內在指導性作用[18]。粒子群優化算法因其結構簡單、便于實現、輸出結果精度高、收斂速度快等優點，被應用于約束優化、動態多目標優化等問題，并取得了很好的效果[19]。鑒于粒子群算法在處理非線性問題的突出效果，故在BiLSTM 超參數的選取上使用PSO 優化算法[20]。

該算法的核心是根據個體歷史最優解與全局歷史最優解來更新粒子的速度和位置，更新公式為：

式中：vid為速度；c1，c2為粒子的加速學習因子；t為迭代次數；xid為當前位置；w為慣性權重；r1，r2為隨機數；pid，pgd分別為粒子自身最優值和全局最優值。

通過迭代更新各個粒子的位置與速度。搜索過程中得出最佳方程解即全局最優解。當群體搜索到滿足最小適應值的最優位置結束計算。

本文將PSO 應用于BiLSTM 網絡的隱含層神經元個數、周期次數、學習率、批大小等相關參數進行尋優，進一步提升BiLSTM 網絡的預測精度。

2 PSO-BiLSTM 預測模型

PSO-BiLSTM 預測模型構建步驟如下。

（1）了解分析聯合循環發電廠，再通過主成分分析，獲得聯合循環機組性能表現的主要影響因素。將這些因素選取并作為主要特征輸入到BiLSTM 模型。

（2）初始化PSO-BiLSTM 模型的網絡參數，確定輸入層。xi表示聯合循環發電廠的輸出功率影響因素。將這些主要參數輸入到網絡中進行學習，而輸出為未來某一時間段的輸出功率預測值。

（3）BiLSTM 模型設置3 層隱藏層。每層有30 個神經元，4 個輸入量，激活函數為tanh 函數和sigmoid 函數，周期次數為9，初始學習率為0.001。

（4）根據損失函數RMSE 獲得輸出誤差。結合PSO 算法調節樣本權重并不斷更新Bi-LSTM 中的參數，直到迭代收斂或達到最大迭代值時結束。

（5）得到PSO-BiLSTM 預測模型并對模型輸出值反歸一化，得到并輸出最終預測結果，完成預測。

基于PSO-BiLSTM 模型的預測流程圖如圖4所示。

圖4 PSO-BiLSTM 模型流程圖Fig.4 PSO-BiLSTM model flow chart

3 實驗與結果分析

3.1 數據采集分析

采集6年的歷史數據，由9 568個數據點組成，使用的數據集是UCI 數據庫中Combined Cycle Power Plant Data Set 的數據。該電廠被設置為滿負荷運行。為實現對發電量高精度地預測，必須選擇接近最大負荷系數的運行數據，故該數據集符合模型測試的數據對象。原始數據如圖5 所示，表示各時間點對應的輸出功率值。

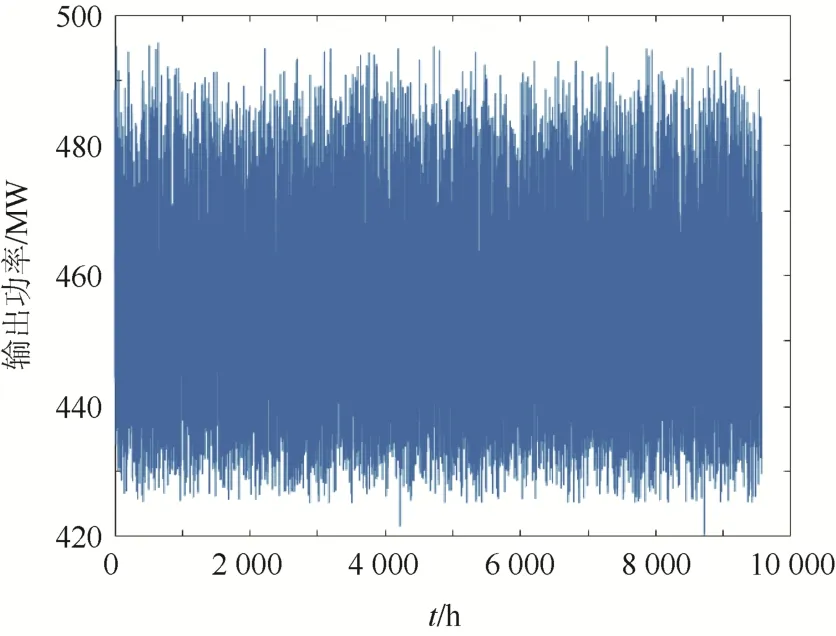
圖5 各時間點輸出功率數據分布Fig.5 Data distribution of output power at each time point

選取原始數據集前90%數據用作訓練集，選取其中96 個點用作測試集，對不同算法及優化組合模型進行實驗。數據描述如表1 所示。

表1 數據集的基本統計數據Tab.1 Basic statistics of dataset

由表可以看出，當聯合循環電廠機組滿負荷工作時，電能輸出功率PE的最小值和最大值相差75.5 MW；這主要受環境因素的波動影響。環境因素對CCPP 機組的輸出功率影響至關重要，并且兩者間關系比較復雜。為建立精確的數學模型以得到復雜的環境因素與功率之間的關系，本文使用PSO-BiLSTM 模型預測聯合循環機組的輸出功率。

聯合循環電廠滿負荷工作條件下，燃氣輪機負荷輸出對環境因素反應較為敏感，汽輪機負荷輸出對排氣真空度敏感、特征變量間的關系由相關性分析得出，如圖6 所示。環境變量溫度和排氣真空度與發電輸出功率呈強負線性關系，環境壓力和濕度與發電輸出功率呈弱正線性關系。由圖6 可知，溫度和排氣真空度是發電輸出功率的主要控制變量，而剩余的環境壓力和濕度等變量經多次實驗得出仍對預測的輸出結果有影響。最終考慮4 個主要特征作為輸入變量。因此，本文是在同時使用4 個特征的前提下進行訓練的。

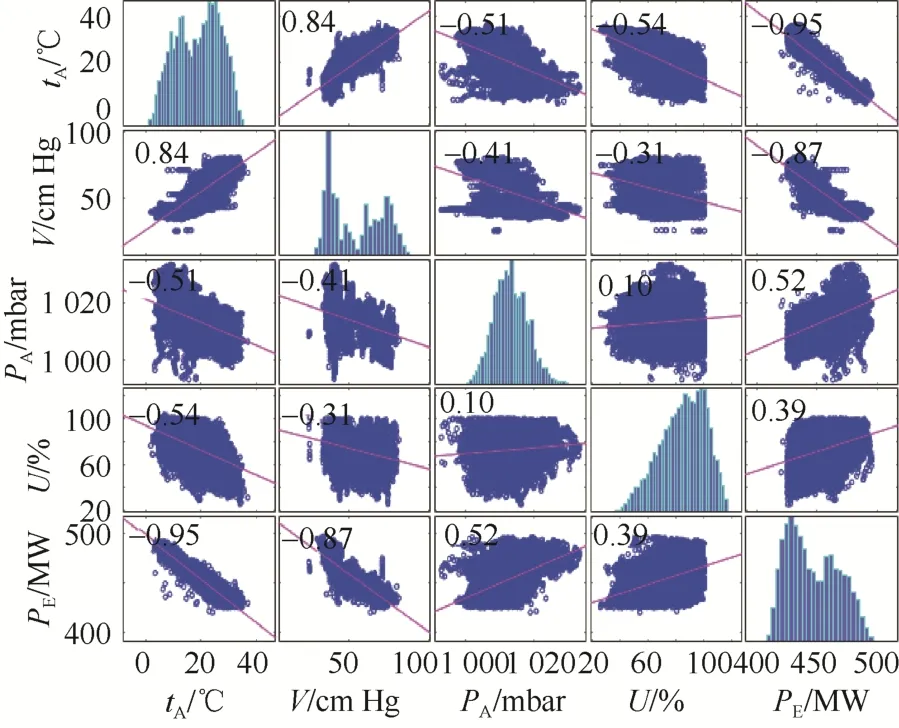
圖6 特征相關矩陣Fig.6 Characteristic correlation matrix

3.2 實驗環境

使用MATLAB2020a 搭建模型并訓練。實驗運算條件：主機時鐘頻率3.20 GHz，Inter Core i7-8700處理器，內存為16 GB，硬盤為512GBPCIe3.0固態。

3.3 歸一化

聯合循環電廠數據集中的環境變量（溫度、環境壓力、相對濕度）和排氣真空變量等主要特征數據與用于預測電廠的每小時凈電能輸出數據相比波動幅度較大，且數據之間的量綱不同，必須進行歸一化處理。

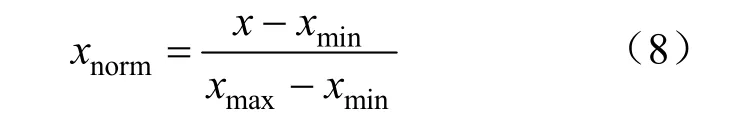
式中：x為原始輸出功率數據；xmin為原始數據的最小值；xmax為原始數據的最大值；xnorm為歸一化后的結果。

3.4 模型的評價標準

對于常見的預測算法，預測精度評價指標有平均絕對誤差和均方根誤差。本文選取的評價指標及表達式為：

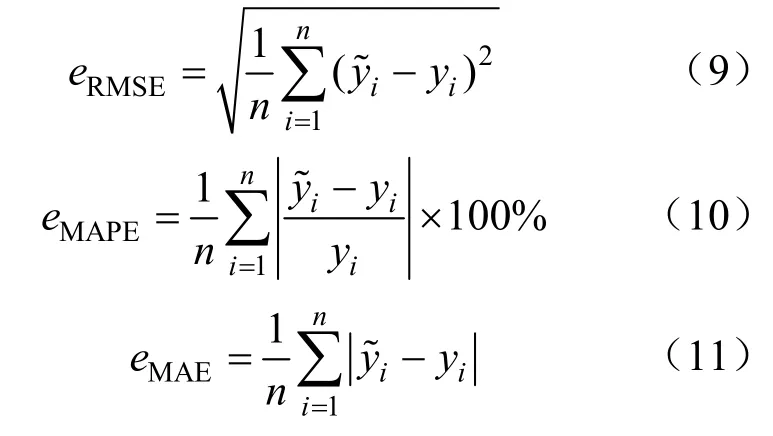
3.5 實驗過程及結果分析

在BiLSTM 模型中，關鍵超參數對模型整體性能的影響較大，分別為：3 層隱含層神經元個數、周期次數、學習率和批大小值。

PSO 優化BiLSTM 模型參數的具體步驟如下。

步驟1：對聯合循環電廠的環境溫度、環境壓力、相對濕度、排氣真空等主要特征數據，以及用于預測電廠的每小時凈電能輸出數據進行預處理。

步驟2：初始化粒子群參數。超參數初始設置：自我學習因子為0.5，群體學習因子為0.5，慣性權重為0.8，種群規模為20。

步驟3：構建BiLSTM 預測模型，確定參數尋優范圍。BiLSTM 中原始隱含層個數分別為34，50，24；學習率為0.001，周期次數為9，批大小值為24。待優化參數：3 個隱含層個數取值范圍L1,L2,L3?[1,100]，周期次數取值范圍為e?[1,30]，學習率取值范圍為Lr?[0.001,0.3]，批大小取值范圍為b?[1,150]。生成一個種群粒子，將這6 個關鍵超參數作為粒子尋優參數變量，確定參數的尋優范圍。

步驟4：設置的適應度函數為均方根誤差。將這6 個關鍵超參數作為粒子尋優的特征，并作為待優化參數輸入到PSO 算法中并進行初始化；將初始化后的值作為歷史最優值賦值給雙向長短期記憶神經網絡，計算粒子的適應度值；根據粒子適應度值的不同進行評估，確定粒子的全局最優位置與局部最優位置，并作為其歷史最佳位置記錄。

步驟5：根據公式（6）（7）對普通粒子和局部最優粒子位置及速度更新。

步驟6：判斷粒子能否終止迭代。原始BiLSTM預測模型的均方根誤差值為4.54，將均方根誤差值定為尋優目標且小于4.0 設為系統要求。若經過粒子群優化后的模型最終得到的均方根誤差值小于4.0 或達到最大迭代次數即得到最優參數，則停止訓練，輸出此時的優化參數數值，同時輸出最終的模型；否則重復步驟5。

尋優過程適應度變化曲線如圖7 所示。基于PSO 算法的各個參數尋優過程見圖8。參數最終的尋優結果：前3 層隱層神經元個數分別為27、30 和30，周期次數為9，學習率為0.023 7，批大小值為12。

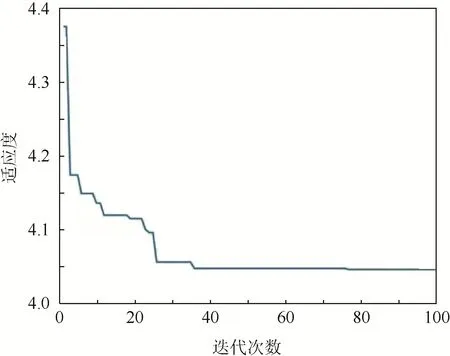
圖7 適應度變化曲線Fig.7 Fitness change curve

圖8 最優粒子的尋優過程Fig.8 Optimization process of optimal particle

為了驗證PSO-BiLSTM 預測模型的性能，使用相同實驗數據集，將本文模型與LSTM 模型、PSO-LSTM 模型、BiLSTM 模型進行對比實驗。

采取多次實驗取平均值分析結果，表2 為隨機10 次模型平均誤差對比實驗結果。傳統的LSTM 模型、BiLSTM 模型、PSO 優化LSTM 的模型和PSO-BiLSTM 模型4 種方法的預測結果如圖9 所示。

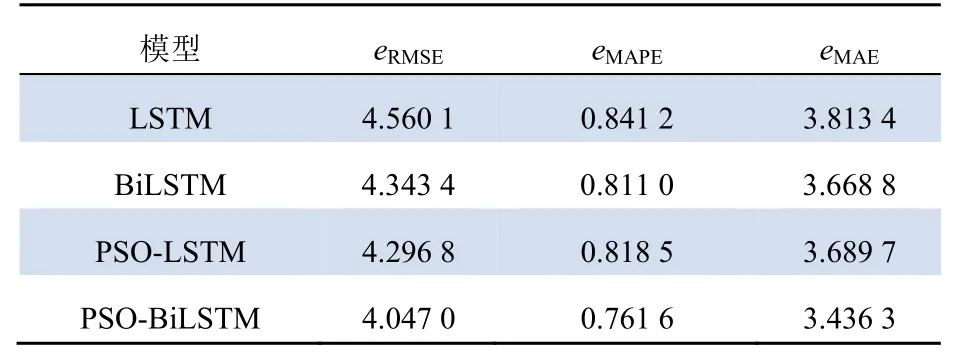
表2 隨機10 次模型平均誤差對比結果Tab.2 Comparison of model average error of random 10 times

圖9 LSTM、BiLSTM、PSO-LSTM 與PSO-BiLSTM 預測對比結果Fig.9 Comparison of prediction of LSTM、BiLSTM、PSO-LSTM and PSO-BiLSTM

實驗結果表明，LSTM 和BiLSTM 模型預測的均方根誤差分別為4.560 1、4.343 4，而PSO-LSTM模型與本文提出的PSO 優化BiLSTM 模型的均方根誤差分別為4.296 8、4.047 0。在基礎模型上，雙向特性的BiLSTM 模型能夠訓練學習更多的信息，所以各個評判誤差均小于單向LSTM 模型；且經PSO 優化超參數后的模型，其預測值更接近真實值。與基礎模型的預測效果對比可知，優化后的模型預測精度進一步提升，說明利用PSO 算法優化BiLSTM 模型參數能夠明顯提高電廠輸出功率預測的精確性。

將該模型與GM，BP，GRNN 和Elman 等網絡模型進行了比較，結果如圖10 所示。

圖10 不同模型預測結果對比Fig.10 Comparison of prediction results of different models

圖10 為不同模型預測結果對比圖。由圖10可以看出，長短時記憶網絡預測結果相較其他模型能更好地貼合真實數值；且相對數據集而言的某些離群點，PSO-BiLSTM 模型比LSTM、BiLSTM、PSO-LSTM 預測精度更高。

表3 為各模型預測誤差結果。結果顯示，以LSTM 算法為基礎的模型精度更高。LSTM、BiLSTM、PSO-LSTM 和PSO-BiLSTM 的平均預測誤差分別為0.841 2%、0.811 0%、0.818 5%、0.761 6%；采用PSO-BiLSTM 模型的預測精度相比LSTM、BiLSTM、PSO-LSTM 分別提高了9.462 7%，6.091 2%，6.951 7%。

表3 各模型預測誤差結果Tab.3 Prediction error results of each model

在PSO 優化方面，不論是針對LSTM 還是BiLSTM，本文模型上都體現了超參數優化對模型預測精度的提升效果。采用PSO 優化的模型的誤差相比原模型LSTM 和BiLSTM 分別減少了5.774 0%，6.824 1%。經PSO 優化后模型預測精度比原模型更高，且PSO-BiLSTM 模型預測精度最優，充分體現了Bi-LSTM 對數據的利用率更高。所以，PSO-BiLSTM 模型可有效提高聯合循環電廠輸出功率預測精度。

圖11 為BiLSTM 與PSO-BiLSTM 模型的部分誤差對比。從圖11 中可看出，優化后的BiLSTM模型數據真實誤差相對更小。

圖11 BiLSTM、PSO-BiLSTM 模型誤差對比Fig.11 Comparison of errors between BiLSTM and PSO-BiLSTM models

4 結論

針對聯合循環電廠發電能力隨環境溫度、壓力、相對濕度和電力需求等條件變化影響造成預測精度較差的問題，提出使用粒子群算法與具有較強泛化能力和雙向特性的BiLSTM 模型相結合的PSO-BiLSTM 預測模型。并利用UCI 數據庫中數據集進行性能驗證。

針對BiLSTM 訓練過程中遇到的調參問題，引入PSO 算法對BiLSTM 網絡模型的相關超參數進行優化，使優化后的PSO-BiLSTM 模型不僅能實現自動調參，而且其預測精度得到提高。

實驗分析表明，本文所提PSO-BiLSTM 模型在聯合循環電廠輸出功率的預測方面精度最優，驗證了本文所提方法的有效性和可行性。