不同校中狀態對某軸系回旋振動的影響研究

劉金林，賴國軍，，姜忠龍，曾凡明

（1.海軍工程大學 動力工程學院，武漢 430033；2.中國人民解放軍 91404部隊，河北秦皇島 066001）

0 引 言

船舶推進軸系回旋振動是指軸系旋轉過程中，由轉動部件自身的不完全對稱性和螺旋槳在不均勻流場中工作所產生的交變力矩引起的周期性的彎曲現象。影響軸系回旋振動特性的因素有很多，比如軸系本身的結構屬性、螺旋槳的陀螺效應、軸承支點的數量和位置、中間軸數量和軸承間距等等[1-2]。

軸系回旋振動不僅會產生較大的振動噪聲，影響船舶舒適性，而且還會嚴重影響船舶的安全運行，增大軸頸與軸承的磨損，破壞船舶艉軸的密封裝置，劇烈的回旋振動甚至會引發軸系斷裂。因此，軸系回旋振動問題一直是國內外研究的熱點。賴國軍等[3-5]綜述了近年來船舶推進軸系設計的研究現狀，指出了提高船舶推進軸系設計質量的幾個關鍵問題，如軸系校中、軸系振動及軸系設計流程等的優化問題。另外，他們也研究了軸系的多學科綜合優化問題。周海軍等[6]在傅里葉級數基礎上，結合船舶推進軸系的特點并考慮螺旋槳的回旋效應，重新推導了帶集中質量點的多跨梁結構的回旋振動計算公式，并針對某軸系研究了它在額定工況下正逆回旋振動的動態特性。Bouaziz、Grossi 和周瑞平等[7-10]研究了軸系中間軸承不同布置位置、支撐剛度變化和取消中間軸承對軸系回旋振動特性的影響，為軸系的設計、校中安裝提供了一定的理論基礎。

本文以某軸系試驗平臺為研究對象，采用有限元對其進行了直線校中和軸承位置雙向優化校中。基于流體動力潤滑理論，建立軸承油膜支撐模型，計算軸系不同校中狀態下各軸承油膜分布情況，據此得到各軸承支撐剛度，并計算和對比得到軸系不同校中狀態對軸系回旋振動的影響，為在軸系設計階段控制其回旋振動提供一定的理論支撐。

1 軸系試驗平臺簡介

本文以某型電力推進軸系試驗平臺為研究對象，其布置簡圖如圖1所示。

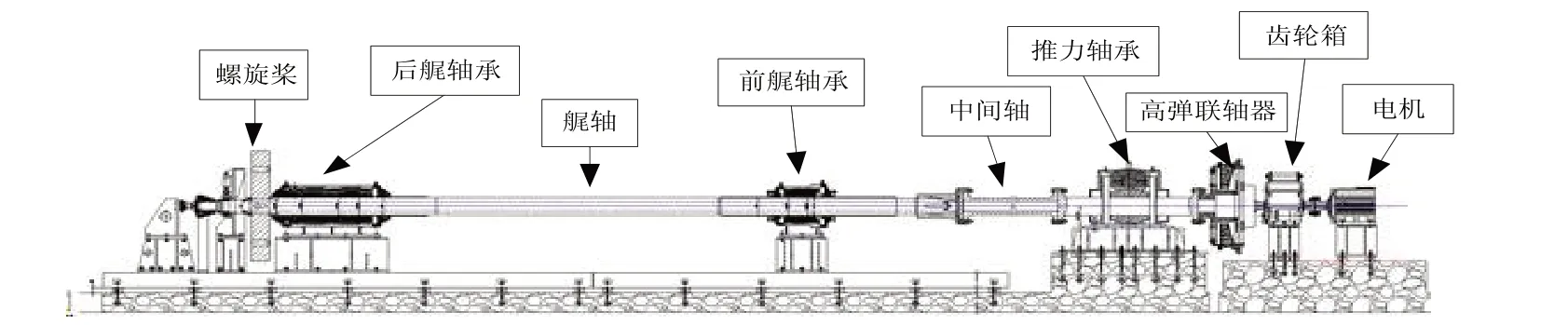
圖1 某軸系試驗平臺布置簡圖Fig.1 Sketch of a shafting testing platform

該軸系試驗平臺主要組成部件有螺旋槳（用圓盤代替）、艉軸、后艉軸軸承、前艉軸軸承、中間軸、可拆聯軸器、推力軸承、高彈聯軸器、齒輪箱、電機等。艉軸與中間軸通過半聯軸節連接，中間軸與推力軸之間通過法蘭連接。該軸系試驗平臺中的前艉軸承和后艉軸承都是水潤滑，推力軸承是滑油潤滑。文中在考慮軸承潤滑特性時，各軸承都稱作油膜潤滑，但在計算時對潤滑液體的不同屬性分別做了不同的處理。

2 軸系校中計算及對比

2.1 軸系直線校中

根據軸系試驗平臺的實際尺寸和相應約束條件，建立如圖2所示的有限元模型。

圖2 軸系試驗平臺有限元模型Fig.2 Finite model of the shafting testing platform

在ANSYS 中定義材料的屬性，設定軸承位置坐標和相關約束條件得到該軸系試驗平臺直線校中下的各軸承狀態參數如表1所示。

表1 軸系試驗平臺直線校中各軸承的狀態參數Tab.1 State parameters of each bearing of the shafting testing platform under its linear alignment

2.2 軸承位置雙向優化校中

由軸系試驗平臺直線校中計算結果可知，由于圓盤的懸臂梁作用引起的軸系試驗平臺后艉軸承上負荷過大，這易導致軸系的橫向激勵過大，引起過大的回旋振動。在此研究優化各軸承的位置使后艉軸承上的負荷f1最小，即軸承位置雙向優化的目標函數為f1的值最小。

式中：f0為軸系直線校中狀態下后艉軸承上的載荷（N）；A1i(yi)為負荷影響系數，第i個軸承垂向變位1 mm后對后艉軸承上載荷相對于直線校中狀態下的變化量（kN/mm）；yi表示第i個軸承的變位值（mm）；f1x是各軸承軸向變位對后艉軸承上載荷的影響。

由2.1節軸系直線校中結果（各軸承上的支反力）可求得軸系各軸承間的負荷影響系數矩陣為

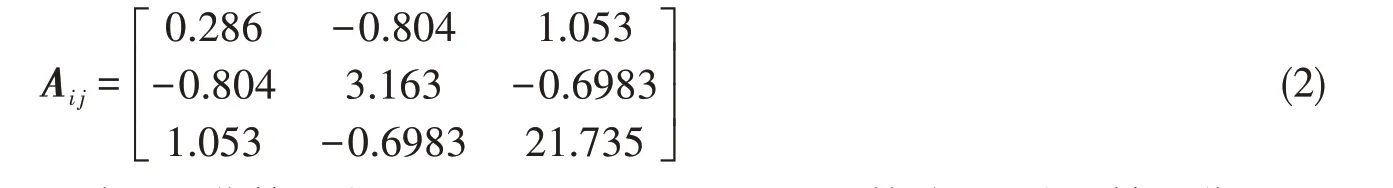
在軸系設計相關約束條件下，采用野草算法（Invasive Weed Optimization，簡稱IWO）對軸承位置進行雙向尋優。即尋優過程的自由變量為（xi,yi）（i=1,2,3），其中，xi為各軸承的軸向變位，yi為各軸承的垂向變位。

參考軸系試驗平臺直線校中方法，在ANSYS中建立其有限元模型，軸系采用Beam 188梁單元，在軸系末端加載一集中載荷代替圓盤（螺旋槳）的重量，并假設軸承為剛性支撐，用Combin 214 單元模擬。因此，可知野草變量的維數為D=6。該軸系軸承位置進行雙向優化的IWO 算法所需的基本參數可用表2表示。

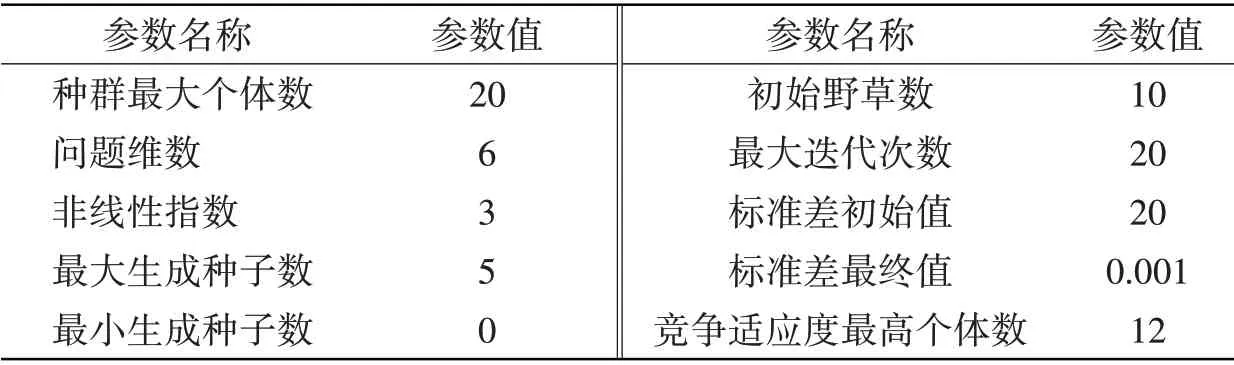
表2 IWO算法基本參數Tab.2 Basic parameters of IWO algorithm

IWO 算法通過Matlab 程序實現野草個體的適應度函數調用及運算，采用ANSYS 程序計算野草個體相對應的軸系校中計算，其具體優化過程如圖3所示。

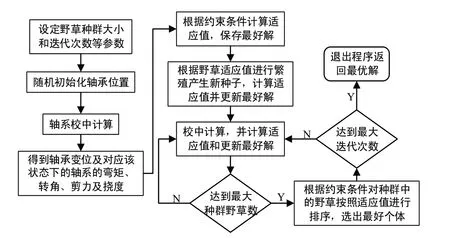
圖3 軸系校中優化IWO計算過程Fig.3 IWO calculation process of shafting alignment optimization

采用IWO 算法，經過100 次迭代后，得出目標函數值（后艉軸承上的載荷）最終收斂于49.677 kN。并且得到軸承位置雙向優化后各軸承的位置及其校中優化狀態分別如表3和表4所示。

表3 軸系試驗平臺雙向優化前、后各軸承位置Tab.3 Positions of each bearing before and after the shafting testing platform dual optimal alignment

表4 軸系試驗平臺雙向優化校中各軸承的狀態Tab.4 State parameters of each bearing of the shafting testing platform under its dual optimal alignment

3 軸承支撐特性研究

3.1 軸承支撐油膜特性分析

軸承支撐系統（軸承基座、軸承支撐油膜和船體等）本身是一個彈性體，其剛度會隨軸系的校中狀態和運行工況的變化而變化。尤其是各軸承支撐油膜，其剛度特性與油膜的壓力和厚度有關，需要把它當作非線性問題來研究。基于滑動軸承動壓潤滑理論[11-12]，采用雷諾方程計算軸承支撐油膜壓力分布，為簡化計算，假設軸系運行過程中，軸承溫度不變，不考慮油膜體積變化，油膜為層流，忽略慣性力的影響。

圖4為滑動軸承在軸系正常運轉時，受到載荷F的作用，軸頸中心O2與軸承中心O1之間有一個偏心距離，它們的偏心距為e，偏心角為θ；軸承與軸頸間圓心距O1O2向兩端的延長線與軸承和軸頸相交，兩交線線段分別表示軸承和軸頸之間的最大間隙hmax=c+e和最小間隙hmin=c-e，其中c為軸瓦與軸頸之間的半徑間隙，r+c為軸承孔內徑，r為軸頸半徑；沿軸系旋轉的方向ω，軸承和軸頸之間的間隙由hmax變化至hmin，是一個收斂的楔形，在這段間隙變化區間，油膜承受的壓力是先逐漸增大后急劇減小的，該楔形油膜主要是由軸承承受的載荷F形成。

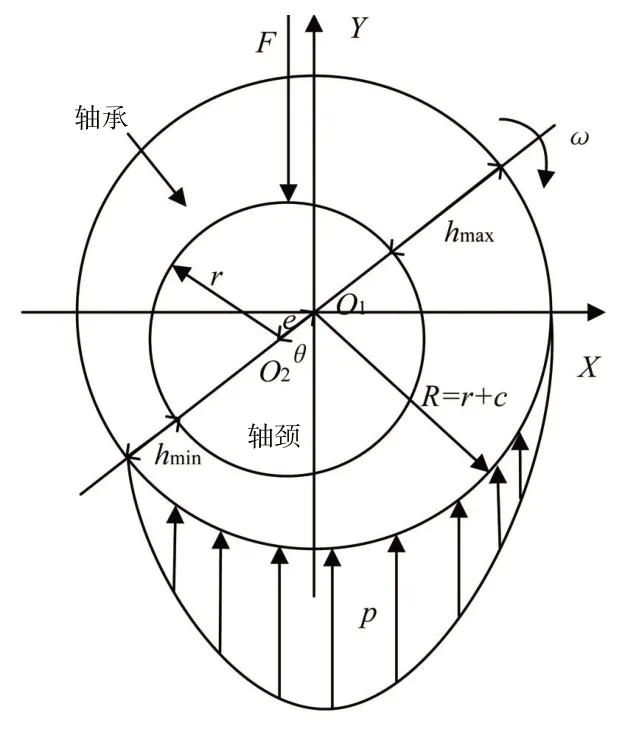
圖4 軸承支撐油膜壓力分布示意圖Fig.4 Schematic diagram of pressure distribution of bearing support’s oil film

軸系在不同的校中狀態和不同運行工況下，軸承所受的載荷、軸承-軸頸的偏心距e和偏心角θ是各不相同的，軸承所受的外載荷F、軸承-軸頸的偏心距e和偏心角θ等因素會直接影響到各支撐軸承上的油膜壓力分布。因此，研究不同校中狀態對軸系回旋振動的影響，必須計算不同校中狀態下，各軸承上的油膜壓力分布和剛度與軸系運行工況之間的關系。

3.2 軸承支撐油膜壓力計算

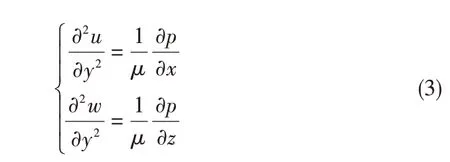
圖5 為軸瓦與軸頸間油膜示意圖，用于分析支撐軸承油膜的壓力分布情況。圖中h代表軸承支撐油膜的厚度，u、v、w分別表示軸承支撐油膜在空間直角坐標系X軸、Y軸、Z軸方向上的分量。結合流體層流理論，假設粘度和體積不變，建立雷諾方程為

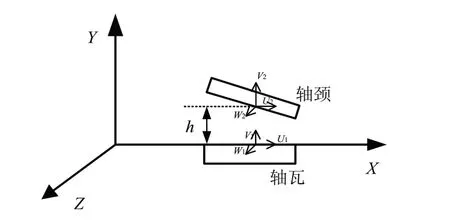
圖5 軸瓦與軸頸間油膜示意圖Fig.5 Schematic diagram of oil film between bearing bush and journal

式中，μ為油膜粘度，ρ為滑油密度，p為油膜所受壓力。

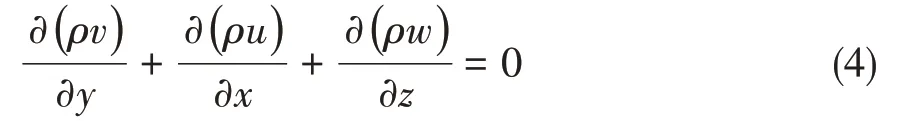
聯立式（3）和式（4），得

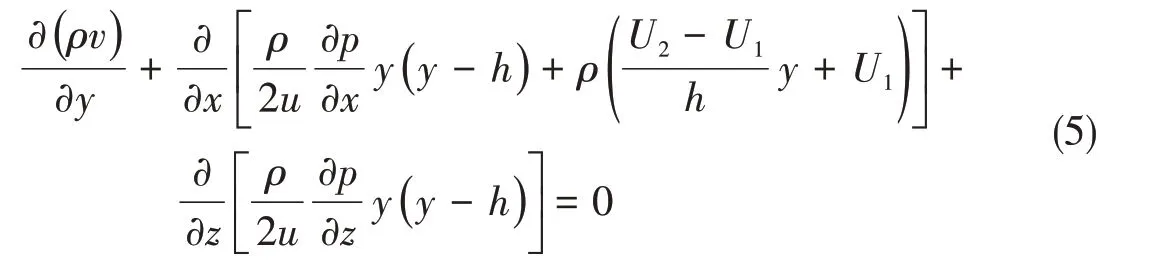
根據圖5可知在該狀態下的邊界條件為

求解油膜支反力，根據式（6）的邊界條件和油膜體積不可壓縮性，聯立式（5）得

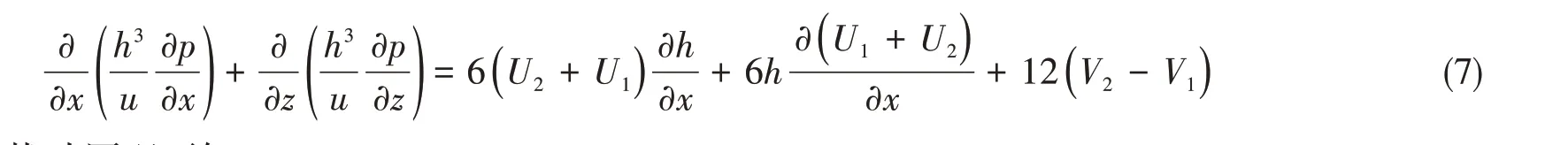
根據小擾動原理可知：

軸系運轉過程中，軸瓦是靜止的，且軸瓦和軸頸的材料剛度遠大于油膜剛度，故忽略軸瓦與軸頸變形，將式（8）代入式（7）可得到該支撐油膜的雷諾方程式為

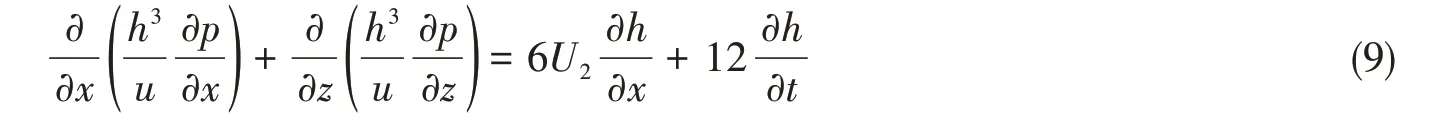
將式（9）轉化為圓柱坐標，可得

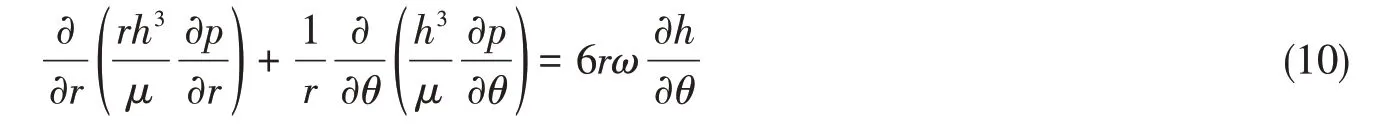
式中，r為徑向坐標（mm），μ為油膜的動粘度系數（Pa·s），θ為軸向坐標（rad），ω為軸系轉速（rad/s）。對支撐軸承油膜壓力分布積分，可得軸承油膜支反力在圓柱坐標下的表達式為

聯立式（3）～（11），根據軸系各軸承上的載荷、軸承—軸頸偏心角和偏心距，就可求得該軸系在穩定工況下的油膜壓力分布。

3.3 不同工況下各軸承油膜壓力

3.2節給出了該軸系試驗平臺在穩定運行時，支撐軸承油膜壓力分布的計算方法。但在船舶運行過程中，軸系的工況是隨時變化的，將不可避免地對支撐軸承油膜產生一個隨時間變化的擾動作用。當軸系轉速發生變化時，各支撐軸承油膜壓力分布可由下式表示：

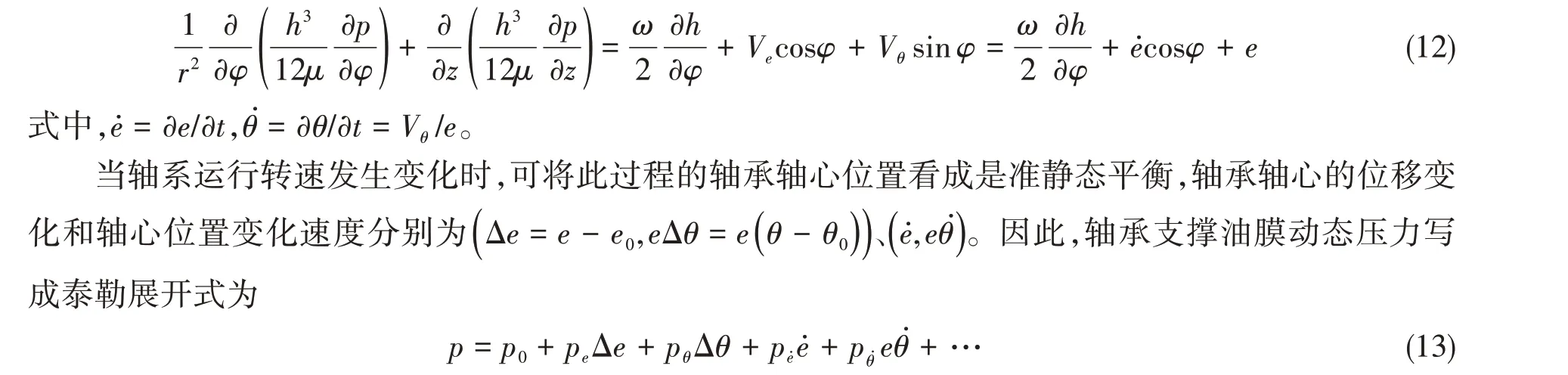
式中，pe為油膜動壓力對軸心偏心距e的偏導數，pθ為油膜動壓力對軸心偏心角θ的偏導數，pe˙為油膜動壓力對軸心偏心距變化率e˙的偏導數，pθ˙為油膜動壓力對軸心偏心角變化率θ˙的偏導數。

綜上，編寫該軸系試驗平臺各軸承支撐油膜壓力分布計算程序，可計算求得軸系在直線校中和軸承位置雙向優化校中狀態下，任意正常工況下各軸承上油膜壓力分布。該軸系在以上兩種校中狀態下，20%額定工況下運行時三軸承上油膜壓力分布結果如圖6所示：

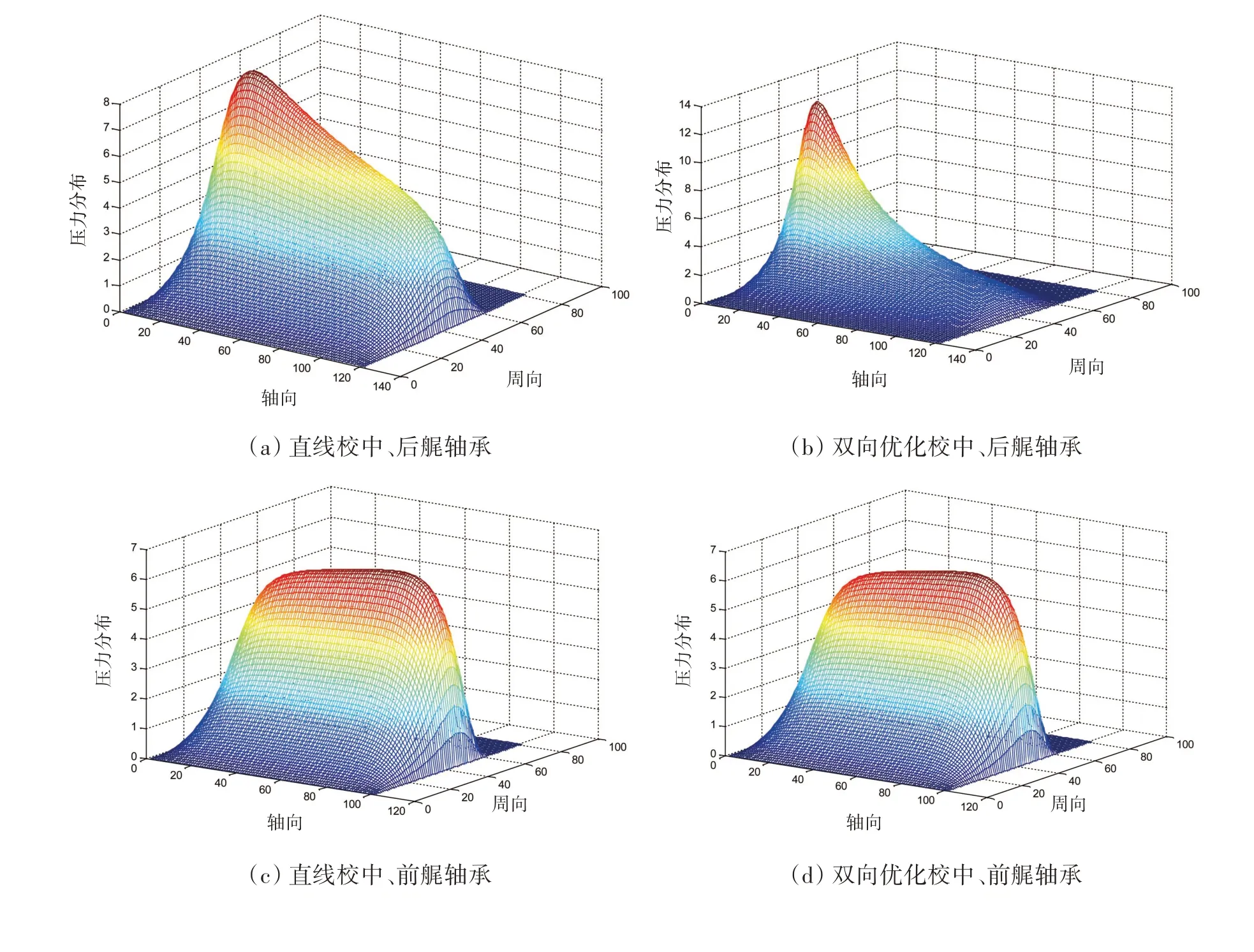
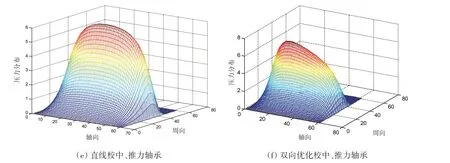
圖6 兩種不同校中狀態下的各軸承支撐油膜壓力分布Fig.6 Pressure distribution of each bearing’s support oil film under two different shafting alignment states

由圖6 可知：該軸系經過軸承位置雙向優化校中后，后艉軸承靠近圓盤端油膜壓力增大（壓力最高值有所增加），另一端油膜壓力有所減小，故造成油膜壓力中心點位置相對于直線校中狀態更接近于螺旋槳端；但根據油膜壓力積分可知，經過軸承位置雙向優化校中后該軸承上的支反力減小了。這是因為進行軸承位置雙向優化后，后艉軸上的靜態載荷由直線校中狀態下的58.49 kN 減小到49.677 kN；前艉軸承上油膜壓力中心點向靠近推力軸承方向移動了；推力軸承上油膜壓力分布增加且壓力中心點向靠近艉軸端移動，這是因為該軸系試驗平臺經過軸承位置雙向優化校中后，前艉軸承與推力軸承中心點距離減小且推力軸承上的靜態載荷由直線校中狀態下的44.81 kN增大至272.89 kN。

聯立式（11）和式（13），當軸系變工況時，軸承支反力的二次泰勒展開式為

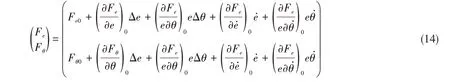
根據物體剛度定義，可得油膜剛度K為油膜力變化率與油膜厚度變化率的比值：

經計算求解可得，該軸系試驗平臺在20%額定轉速下，兩種校中狀態下各軸承上支撐油膜水平方向和豎直方向的剛度如表5所示：

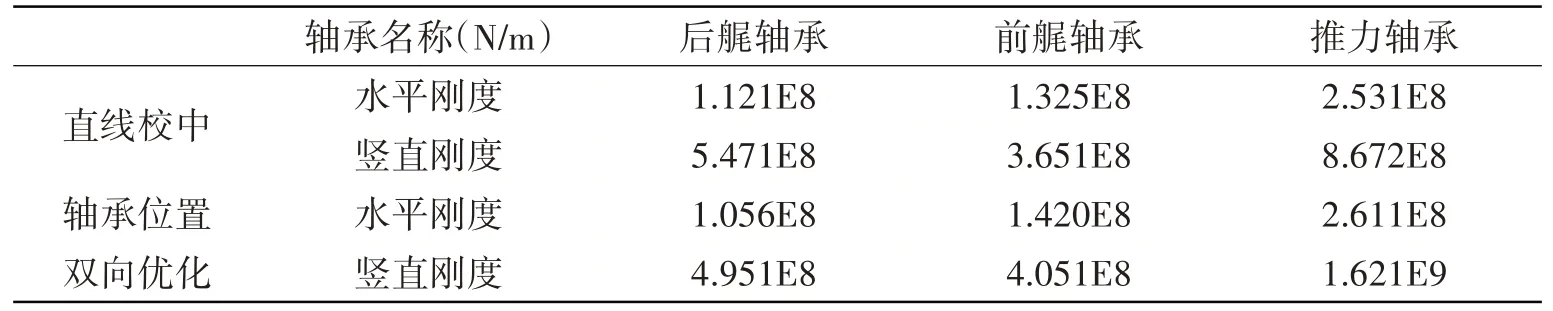
表5 軸系試驗平臺20%額定轉速下各軸承的油膜剛度Tab.5 Stiffness of each bearing at 20%rated speed of the shafting testing platform

該軸系試驗平臺的兩種校中狀態，其他不同運行工況下各軸承上的油膜壓力分布及其剛度可用類似的方法求得。

3.4 軸承支撐模型的建立

軸系的回旋振動特性與各軸承的支撐特性緊密相關，為了研究軸系不同校中狀態對其回旋振動的影響，需要根據軸系在不同校中狀態下各軸承的支撐特性，建立各軸承的支撐模型。在軸系的三個軸承位置分別建立如圖7所示的支撐軸承單元模型。

圖7 中，Kzz和Czz分別代表了支撐軸承單元在水平方向的剛度和阻尼；Kyy和Cyy分別代表了支撐軸承單元在豎直方向上的剛度和阻尼；Kzy、Kyz、Czy和Cyz分別為該單元在水平方向與豎直方向的耦合剛度和耦合阻尼。

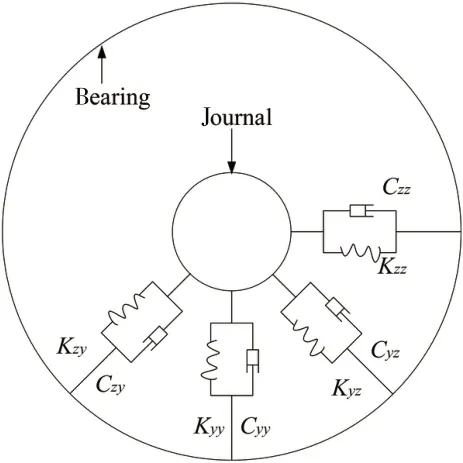
圖7 支撐軸承單元模型Fig.7 Model of support bearing unit

4 軸系試驗平臺回旋振動計算

4.1 回旋振動模態分析

根據第3章求解得到各支撐軸承的水平方向、豎直方向的剛度，建立它們各自的剛度矩陣。采用有限元方法，將軸系離散成有限個小軸承支撐單元，單元與單元之間通過節點聯系起來，軸系的位移、所受力和力矩通過節點傳遞。軸系各節點處的狀態可結合振動方程求得：

為研究不同的軸系校中狀態對回旋振動影響，在得到不同軸系校中狀態下各軸承的油膜支撐特性的基礎上，需進一步分析各軸承支撐狀態對回旋振動的影響。為此，首先研究各軸承在不同邊界條件下的回旋振動模態，根據式（16）得出如圖8所示的軸系回旋振動前兩階模態的振型。

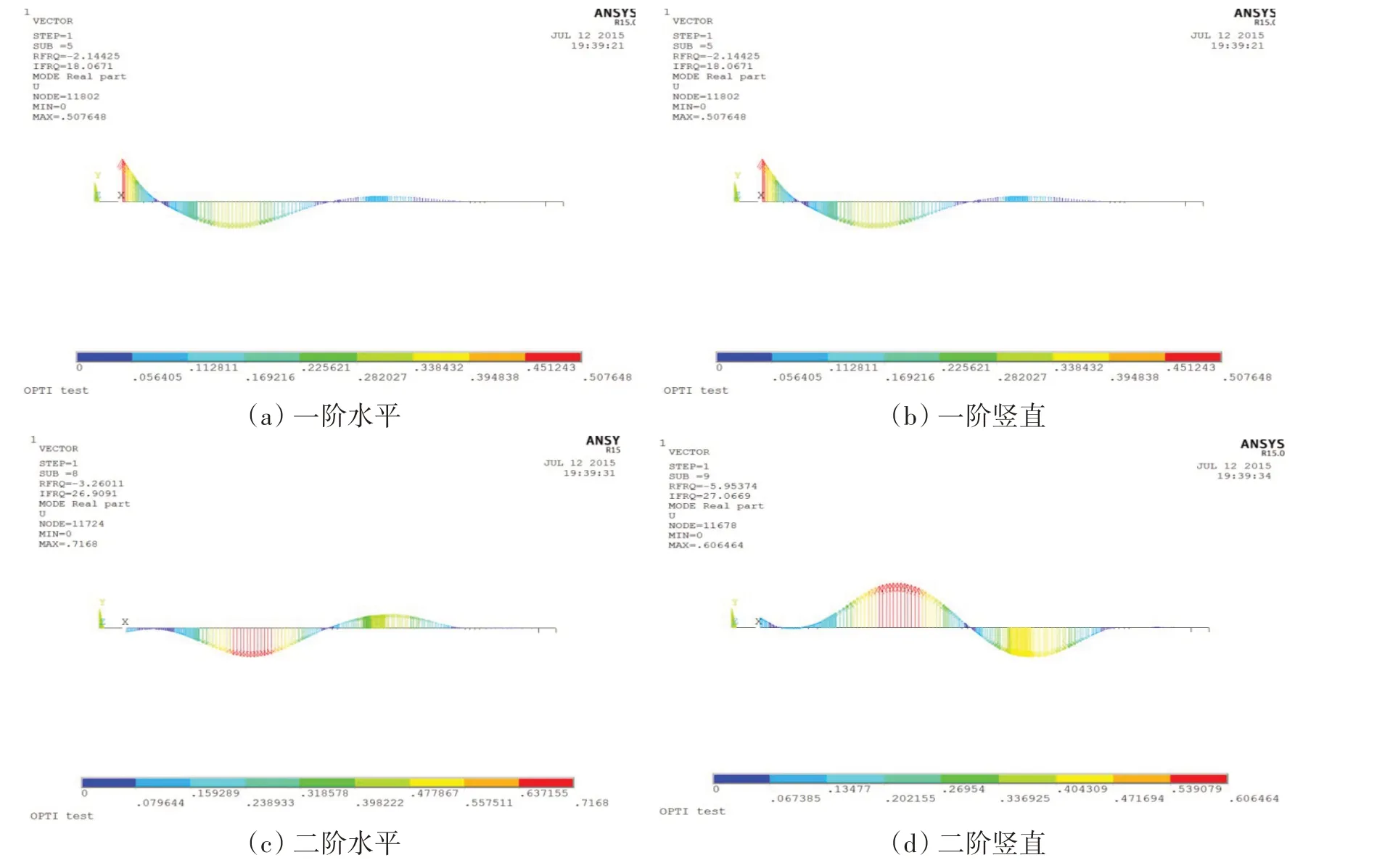
圖8 軸系回旋振動前兩階模態振型Fig.8 First two modal shapes of shafting whirling vibration

圖8（a）和（b）分別顯示了該軸系試驗平臺一階水平和豎直方向的振型；圖8（c）和（d）分別顯示其二階水平和豎直方向的振型。由圖可知：（1）該軸系試驗平臺回旋振動在水平方向的前兩階固有頻率為18.07 Hz和26.92 Hz，豎直方向的前兩階固有頻率為18.96 Hz和27.05 Hz；（2）若軸系的橫向激勵在前兩階回旋振動固有頻率內，則對艉軸和中間軸影響較大。

4.2 不同校中狀態對回旋振動影響對比

為考察軸系的回旋振動幅頻響應情況，根據軸系模態分析結果，選取在軸系回旋振動前兩階固有頻率內，軸系振動較為劇烈的幾個點作為參考點。它們分別為艉軸靠近螺旋槳處一點、艉軸中間點、中間軸和高彈聯軸器附近一點，并依次將它們編號為a、b、c和d參考點。分析軸系上這四個參考點處的回旋振動幅頻響應就可較全面反映該軸系試驗平臺的回旋振動情況。

該軸系試驗平臺處于兩種校中狀態下，四個參考點處回旋振動的幅頻曲線如圖9所示。

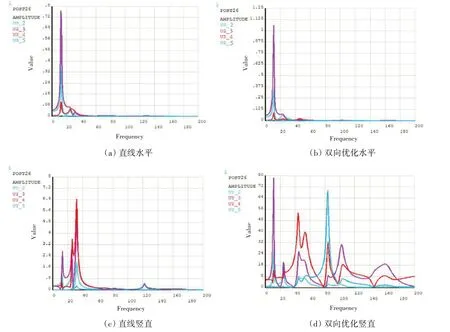
圖9 兩種校中狀態下四個參考點處回旋振動幅頻曲線Fig.9 Amplitude versus frequency of whirling vibration at four reference points under two alignment states

圖9 中的（a）、（b）、（c）和（d）分別顯示了該軸系試驗平臺四個參考點處的回旋振動在水平方向和豎直方向的幅頻曲線，圖中左上角2、3、4 和5 分別表示的是a、b、c和d參考點。由圖可知：（1）同一種校中狀態下，軸系試驗平臺回旋振動水平方向和豎直方向上的共振頻率都相同，不隨軸系轉速變化而變化；（2）同一種校中狀態下，軸系試驗平臺豎直方向上振動幅值明顯大于水平方向，這是因為軸系旋轉過程中，豎直方向的脈沖激勵要大于水平方向；（3）該軸系試驗平臺經過軸承位置雙向優化校中后，其回旋振動一階共振頻率由直線校中狀態下的19 Hz 減小到16 Hz。這是因為軸承位置雙向優化校中后增加了前、后艉軸承中心點的距離，由直線校中狀態下的7022 mm 增加到9088.25 mm；（4）校中優化后，前、后艉軸承中心點距離增大，艉軸段的柔度增加使得b參考點振動幅值增加；（5）因參考點a在軸承附近，故它的回旋振動幅值相對其他參考點較小；（6）軸承位置雙向優化之后，推力軸承上負荷顯著增大，故參考點d豎直方向上的共振幅值增大。

5 結 論

為研究軸系不同校中對其回旋振動的影響，本文根據某軸系試驗平臺實際尺寸建立了有限元模型，并進行校中計算；采用IWO 算法得到該軸系試驗平臺軸承位置雙向優化后的各軸承位置；分別計算了該軸系試驗平臺在直線校中和軸承位置雙向優化狀態下各軸承的水平和豎直方向上的剛度，以此建立軸承—軸頸油膜支撐模型，計算了在不同校中狀態下的回旋振動，得出以下結論：

（1）以艉軸承上負荷最小為目標函數，采用IWO算法可快速得到軸系軸承位置雙向優化結果；

（2）該軸系試驗平臺經軸承位置雙向優化后，艉軸承上的負荷明顯減小，達到了校中優化的目的，但推力軸承上的負荷增大，造成參考點d處回旋振動豎直方向上的頻域響應幅值較直線校中有明顯變大；

（3）軸系的不同校中狀態下，其共振頻率不同，該軸系試驗平臺因軸承位置雙向優化后，前、后艉軸承間的距離比直線校中遠，其回旋振動一階共振頻率由19 Hz減小到16 Hz；

（4）該軸系試驗平臺不同的校中狀態主要影響各軸承豎直方向的支撐特性，因此對其回旋振動豎直方向上的影響大于水平方向。

綜上，該軸系試驗平臺屬于短軸系，以后艉軸承上載荷最小為目標，經過軸承位置雙向優化后軸系的回旋振動較大于直線校中時。故可知軸系的校中狀態對回旋振動有顯著影響，為減小軸系回旋振動，可在軸系校中設計時考慮軸系的振動，設定多目標尋優，尋求校中良好且振動較小的軸系校中狀態。