浮力塔平臺吸力樁承載力研究

潘徐杰，杜守繼，CHEN Weimin，WANG Ge，方智超

（1.上海交通大學船舶海洋與建筑工程學院，上海 200240；2.Wison Offshore Technology Inc.,Houston 77042）

0 引 言

浮力塔平臺是由TLP 平臺及Spar 平臺的發明人Edward E.Horton 與順應式平臺及牽索塔平臺的發明人Lyle David Finn 共同提出的一個新的工作平臺形式[1]。浮力塔采用類似Spar平臺的塔體，與之不同的是，浮力塔通過底部的吸力樁將塔體及上部結構固定在海床上，同時采用順應式平臺的理念隨波浪運動，并且憑借重力與浮力組成的力矩回復。浮力塔多年運營已證明了該技術的可靠性[2]。在浮力塔平臺中，吸力樁是一個核心環節，它在支持浮力塔主體及上層建筑的同時，也承受著上部傳遞下來的風、浪、流力，并且吸力樁的約束也改變了浮力塔的運動特征。由此可見，浮力塔吸力樁基礎的承載特性極其重要[3]。

吸力樁又被稱為吸力沉箱、吸力錨、負壓錨或桶形基礎等，是一種底部敞開、上端封閉的鋼制圓桶結構，也可以做成箱型或其他形狀的結構。1994年7月挪威國家石油公司建成的一座新型大型導管架平臺Europipe16/11E，成功地采用了吸力樁作為其基礎，這也被認為是吸力樁在海洋工程中的首次正式運用[4-7]。隨著Europipe16/11E多年的穩定運營，吸力樁的優勢逐步被接受，各方面的研究也逐步展開，這些工作包括理論方面的研究[8]、試驗方面的研究[9-11]以及數值模擬方面的研究[12-13]，其研究的范圍基本上都是聚焦吸力樁的承載力本身。浮力塔的吸力樁不同之處在于：（1）浮力塔是一種順應式平臺，吸力樁的承載特性關系樁基能否安全作業；（2）周圍土層對吸力樁的約束將改變浮力塔在波浪中的運動形態與幅度，而運動性能也與平臺的安全息息相關；（3）浮力塔的吸力樁處于受壓狀態，這有別于作為系泊點或導管架平臺基礎等處于受拉狀態的吸力樁。以上三點說明浮力塔的吸力樁有別于目前海洋工程界其他形式吸力樁，到目前為止，關于浮力塔平臺吸力樁的承載力研究在文獻中尚未提及。

因此，本文針對浮力塔平臺吸力樁特征，首先結合平臺現場運動的觀測結果，分析了土層對吸力樁的約束情況，并確定了吸力樁的分析工況；其次借助數值模擬手段，分析了吸力樁的承載力，并對比了承載的理論結果與平臺運動的實際觀測值；最后基于承載力分析結果，將土層對吸力樁的約束轉換為土彈簧后對平臺進行運動分析，并對比了運動分析的結果與平臺的實際觀測值。

1 土層對浮力塔吸力樁的約束

浮力塔平臺是一種近似的對稱結構，柱體可采用單柱結構類似于Classic Spar，也可以采用多柱結構類似于Cell Spar。首制浮力塔CX-15 平臺選取了四柱柱體結構，如圖1 所示。如果沒有吸力樁（如圖2 所示）的約束，浮力塔將類似于Spar 平臺在波浪中繞泥線上柱體中的一點做六自由度運動；當吸力樁周圍土層對吸力樁有約束作用時，浮力塔的運動中心將從泥線上柱體中的某一點下移至泥線下的某一點，并且運動的頻率、幅度也將發生根本的改變。

圖1 首制浮力塔平臺CX-15Fig.1 First buoyant tower CX-15

圖2 浮力塔CX-15平臺的吸力樁Fig.2 Suction caisson of CX-15

與平臺在波浪中的運動一樣，周圍土層對吸力樁的約束可以用6×6的矩陣來表示，如式（1）所示。式中k11、k22、k33、k44、k55和k66分別代表土層對吸力樁的縱蕩、橫蕩、升沉、橫搖、縱搖與艏搖的約束，其他項為耦合約束，以k12、k13、k14、k15、k16為例，分別代表縱蕩與橫蕩、縱蕩與升沉、縱蕩與橫搖、縱蕩與縱搖、縱蕩與艏搖的耦合約束，其他各項以此類推。

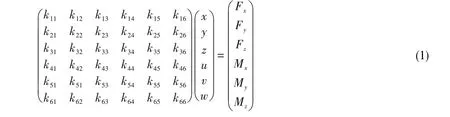
結合平臺的實際運動情況，上述36個約束并非全部起作用，并且鑒于浮力塔平臺是對稱結構（由圖1 和圖2 所示），所以有部分的約束是相同的。浮力塔在波浪中的運動根據現場實際觀測包括橫搖與縱搖運動，以及橫蕩、縱蕩、升沉與轉動的運動趨勢，從而實際起作用的直接約束包括縱蕩、橫蕩、升沉、縱搖、橫搖與艏搖的約束。其中縱蕩與橫蕩的約束相同，縱搖與橫搖的約束相同，雖然在實際運動中有艏搖的趨勢，但鑒于浮力塔在實際工作中未發生轉動，且艏搖與其它自由度運動耦合性弱，故將其忽略，需要關注的直接約束為縱/橫蕩約束k11（=k22）、縱/橫搖約束k44（=k55）與升沉約束k33。而在耦合約束中，以橫蕩與橫搖耦合及縱蕩與縱搖耦合最為重要，這是因為無論在水平力或者是彎矩的作用下，浮力塔平臺的橫蕩與橫搖耦合（或運動趨勢）都是相伴發生的，而縱蕩與縱搖耦合約束鑒于平臺的對稱性與橫蕩及橫搖耦合約束相同，所以需要關注的耦合約束為k15（=-k24=-k42=k51）。

2 浮力塔吸力樁基礎的承載力

以首制浮力塔平臺CX-15 為研究對象，分析吸力樁基礎的承載力。在傳統的吸力樁承載力分析中，最常見的分析工況包括水平方向的承載力和豎直向上的承載力[11]兩個典型工況，其他常見的分析工況諸如斜向上方的拉力等。浮力塔吸力樁的承載力需要結合浮力塔的實際運動情況考慮，根據上述土層對浮力塔吸力樁的約束分析可知，浮力塔吸力樁承載力分析重點包括升沉運動下吸力樁承載力、橫蕩與橫搖（縱蕩與縱搖）耦合運動的承載力兩個方面。

浮力塔吸力樁在升沉運動下的承載力分析，實質上是吸力樁在豎直向下集中力的作用下發生向下的升沉運動，這有別于傳統的吸力樁豎直向上的承載力。在浮力塔的設計中，為了保證由吃水變化所引起的浮力變化不會造成吸力樁的上拔效應，所以在平臺底部設有壓載艙，并用鐵礦砂壓載。以CX-15為例，通過壓載后保證有3000 kN的重量作用在吸力樁上，即使因落潮導致浮力減少，也要保證吸力樁受到向下的力，即浮力塔吸力樁需要考察豎直向下的承載力。

浮力塔吸力樁在橫蕩與橫搖耦合運動下的承載力分析，實質上是吸力樁在載荷的作用下，發生橫蕩與橫搖的耦合運動。這里的載荷可以是水平集中力，也可以是力矩，如果是水平集中力，則該工況與傳統吸力樁的水平承載力分析一致。在本次分析中，橫蕩與橫搖耦合運動下的承載力需要分析在水平集中力單獨作用和彎矩單獨作用的兩個情況，除了考察吸力樁承載力外，還要進一步求得土彈簧對吸力樁的約束剛度。

綜上所述，浮力塔吸力樁承載力研究的模擬分析工況應包括：

（1）吸力樁在向下的集中力Fz作用下，考察吸力樁向下的位移情況；

（2）吸力樁在水平集中力Fx作用下，考察吸力樁的水平位移和搖動情況；

（3）吸力樁在彎矩My作用下，考察吸力樁的水平位移和搖動情況。

2.1 本構模型與參數

首制浮力塔平臺位于秘魯西北沿海Corvina CX-15 水域，水深53.4 m，現場地質勘探的土層分布情況如表1所示，首制浮力塔平臺的吸力樁在泥線下的插深為8 m，結合實際情況，確定在分析吸力樁基礎的承載力時只需要考慮最上面兩個土層。

基于有限元軟件Abaqus，建立樁土相互作用的半圓柱有限元模型，如圖3 所示，吸力樁周圍的土層深度選取為31.4 m，分為兩個土層。由表1 可知這兩個土層均為黏土，并且主要的持力層為軟黏土至硬黏土，而根據海床自然固結以及受到浮力塔平臺豎直向下壓力的實際情況可以判斷，土層符合正常固結與弱超固結的特征，從而選取修正劍橋模型為土的本構模型。依據靜力觸探結果、固結試驗以及三軸壓縮試驗，可以獲得劍橋修正模型的參數，如表2所示。按照首制浮力塔平臺CX-15 實際情況，吸力樁為桶型結構，直徑為8 m，泥線下埋深8 m，吸力樁底部敞開，頂部與浮力塔平臺焊接，在實際建模中忽略浮力塔平臺。根據現場實際觀測，吸力樁強度足夠，平臺運營多年未發現明顯變形，所以模擬中將吸力樁基礎假設為剛體。

表2 劍橋修正模型參數Tab.2 Modified Cam-Clay parameters

圖3 吸力樁基礎有限元模型Fig.3 FEM model of suction caisson

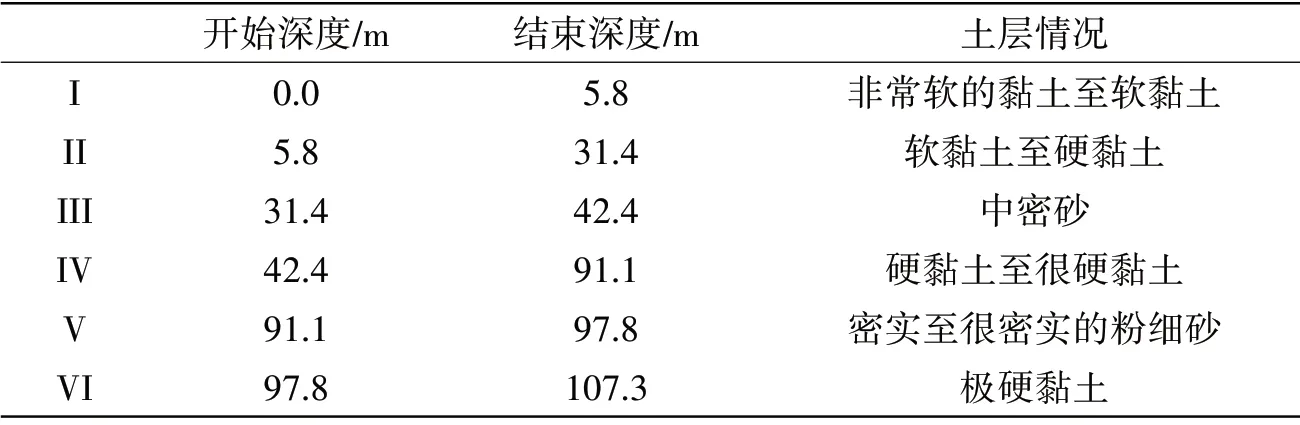
表1 土層分布情況Tab.1 Soil conditions

土層的初始應力、孔隙比、滲透率等根據靜力觸探結果擬合成函數輸入到Abaqus 中作為初始條件。模擬中力的作用點加載于吸力樁頂部的圓心處，在模擬中選取載荷控制法，在模擬中逐步增大施加載荷，監測吸力樁的位移，在模擬中軟土變形過大時終止模擬，此時可認為土壤已經完全進入塑性破壞階段。

2.2 吸力樁在向下的集中力Fz作用下的承載力分析

吸力樁在向下的集中力Fz作用下的承載力分析，從平臺的運動角度上看，就是浮力塔在升沉運動下吸力樁的承載力分析，其P-S曲線結果如圖4所示。

承載力曲線的分析方法有兩種：第一種為直接分析承載力曲線，曲線分為陡變段和緩變段兩段。首先是陡變段，在陡變段中位移隨著載荷的增大而迅速變大，然后出現拐點，出現緩變段，在緩變段中，載荷基本不發生變化而位移迅速增加，陡變段可以近似地認為吸力樁周圍的土層處于彈性階段而緩變段可以認為吸力樁周圍的土層進入塑性破壞階段；第二種方法為對承載力曲線求一次導數得到土彈簧剛度曲線，當剛度較大時，吸力樁周圍土層處于彈性階段，對吸力樁能夠提供足夠的回復力，當剛度消失時，吸力樁周圍土層處于完全塑性階段，對吸力樁已不能提供回復力。

圖4 列出了吸力樁在向下集中力Fz作用下的承載力結果。從圖中可以看出：無論是承載力曲線還是土彈簧剛度曲線，都能清晰地判別出曲線的陡變段和緩變段，但拐點不是特別清晰；但在陡變段和緩變段之間，有一個弧形的過渡段，在這個弧形過渡段中，隨著向下集中力Fz逐漸加大，吸力樁周圍土層的彈性變化逐漸減小，塑性變化逐漸增加，直至最終周圍土層進入塑性破壞階段。

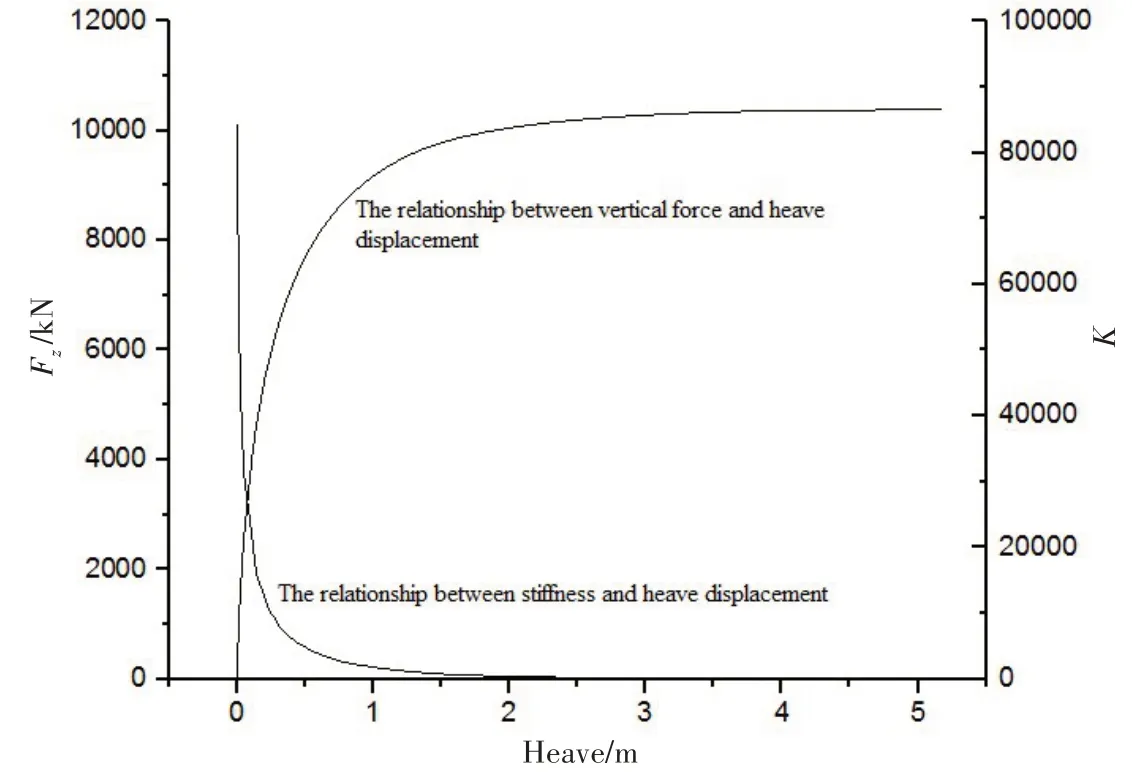
圖4 豎向集中力/剛度與升沉位移的關系Fig.4 Relationship between vertical force/stiffness and heave displacement

從圖4 中可以看出：深沉運動0.2 m 這個點明顯處于承載力的陡變段，即吸力樁的升沉運動在0.2 m 之內，周圍的土層明顯處于彈性階段，此時受到的豎向集中力大約為5000 kN，土彈簧的剛度大約為25 000 kN/m；而當吸力樁在受到8000 kN 以上的豎向集中力時，整個樁基才逐步進入過渡段，此時土彈簧的剛度已小于3000 kN/m。在CX-15平臺的初始設計中，通過壓載使得吸力樁受到3000 kN 的向下壓力，而浮力塔在波浪中升沉運動時，會導致吸力樁受到的壓力在一定范圍內變化。當遇到百年一遇的波谷加低潮位時，吸力樁受到的壓力大約在5000 kN。基于上述分析，顯然可以看出其仍然在安全的范圍內工作，并且3000 kN的初始壓力能保證吸力樁在整個運營期間不會受到上拔力。

2.3 吸力樁在水平集中力Fx作用下的承載力分析

吸力樁在水平集中力Fx作用下的承載力分析，從平臺的運動角度上看，就是浮力塔在水平力作用下吸力樁橫蕩與橫搖耦合運動的承載力分析。其P-S曲線結果如圖5 與圖6 所示，其中圖5 列出了水平力與橫蕩的位移關系，而圖6列出了水平力與橫搖的位移關系。

圖5 和圖6 保持了高度一致的關系，并且與圖4 有著相似的性質，即存在陡變段、過渡段及緩變段。從圖中可以看出，大約在受到1750 kN 時，承載力曲線與剛度曲線逐步進入過渡段，也就是說，樁基周圍的土層塑性變化逐步增加直至完全進入塑性破壞階段。1750 kN 對應的樁基橫蕩位移大約是0.25 m 左右，橫搖角度大約為3.5°。雖然在CX-15 平臺的實際觀測中，無法得知現場的水平力情況，但可以通過實際運動位移來判別樁基安全與否，在實際的位移觀測中，平臺幾乎觀測不到橫蕩運動并且橫搖角度也不超過2°，結合承載力曲線及剛度曲線可以判斷出，吸力樁在安全的范圍內工作。

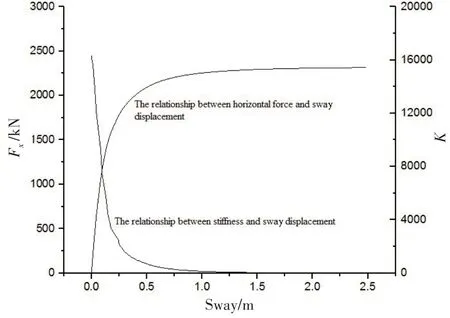
圖5 水平集中力/剛度與橫蕩位移的關系Fig.5 Relationship between horizontal force/stiffness and sway displacement

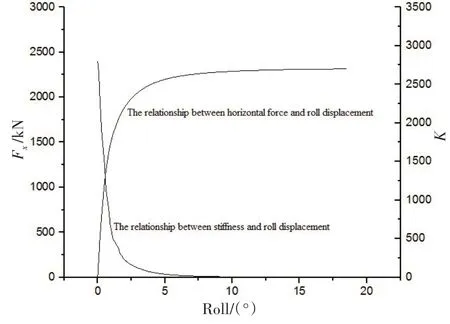
圖6 水平集中力/剛度與橫搖角度的關系Fig.6 Relationship between horizontal force/stiffness and roll displacement

2.4 吸力樁在彎矩My作用下的承載力分析

吸力樁在彎矩My作用下的承載力分析，從平臺的運動角度上看，就是浮力塔在彎矩作用下吸力樁橫蕩與橫搖耦合運動的承載力分析。其P-S曲線結果如圖7 與圖8 所示，其中圖7 列出了彎矩與橫蕩的位移關系，而圖8列出了彎矩與橫搖的位移關系。

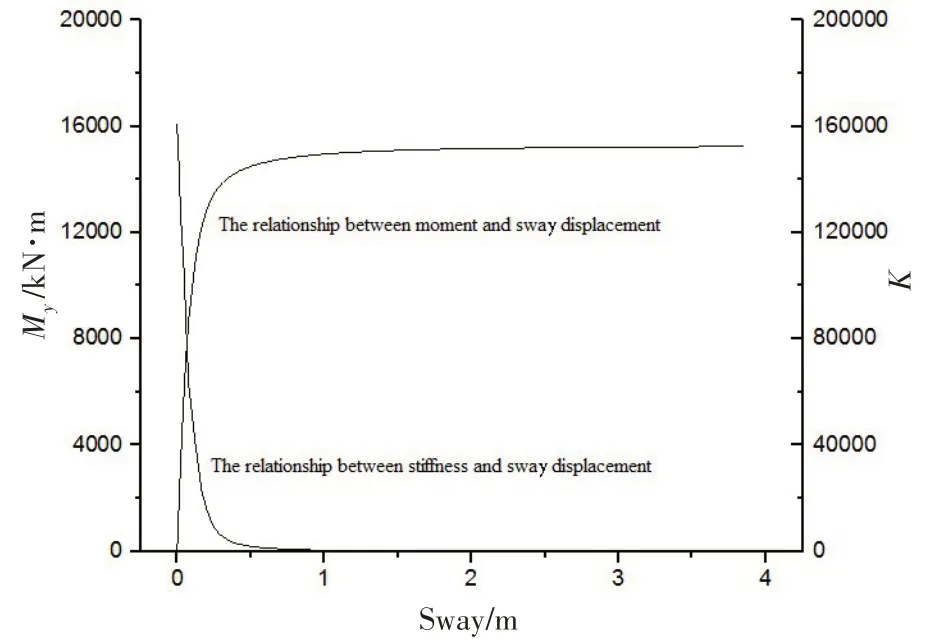
圖7 彎矩/剛度與橫蕩位移的關系Fig.7 Relationship between moment/stiffness and sway displacement

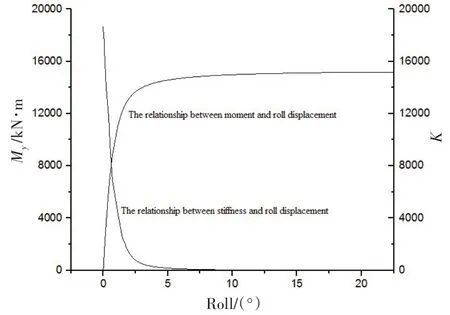
圖8 彎矩/剛度與橫搖角度的關系Fig.8 Relationship between moment/stiffness and roll displacement

圖7 和圖8 保持了高度一致的關系，并且與圖4 有著相似的性質，即存在陡變段、過渡段及緩變段。從圖中可以看出，大約在受到12 000 kN·m 時，承載力曲線與剛度曲線逐步進入過渡段，也就是說，樁基周圍的土層塑性變化逐步增加直至完全進入塑性破壞階段。12 000 kN·m對應的樁基橫蕩位移大約是0.2 m 左右，橫搖角度大約為2.0°。依據前面的分析，結合承載力曲線及剛度曲線可以判斷出，吸力樁在安全的范圍內工作。

3 土彈簧剛度矩陣與運動驗證

在得出浮力塔吸力樁的P-S曲線后，可以將承載力轉化為土彈簧的約束剛度。其中升沉運動下吸力樁P-S曲線可以取陡變段直接通過胡克定律求得吸力樁受到升沉方面的約束剛度。而吸力樁受到的橫蕩約束、橫搖約束以及橫搖橫蕩耦合約束則需要通過水平力作用下吸力樁橫蕩橫搖耦合運動P-S曲線與彎矩作用下吸力樁橫蕩與橫搖耦合運動P-S曲線聯立求解。現只考慮橫蕩、橫搖以及橫搖橫蕩耦合約束作用，故將式（1）簡化為

根據上面的分析結果可知，浮力塔吸力樁均在安全的范圍內工作，所以可以用吸力樁承載力P-S曲線陡變段上的某一點，即取圖5 至圖8 曲線中的某一點，用該點對原點的斜率近似為曲線的割線斜率來進行約束剛度計算。在水平力作用下吸力樁橫蕩橫搖耦合運動P-S曲線中的陡變段，取一個作用力F1，得出對應的吸力樁水平運動幅值X1和轉動幅值θ1，將這3 個值代入式（2）可得式（3）的前兩個方程。在彎矩作用下吸力樁橫蕩橫搖耦合運動P-S曲線中的陡變段，取一個作用彎矩M2，得出對應的吸力樁水平運動幅值X2和轉動幅值θ2，將這3 個值代入式（2）可得式（3）的后兩個方程，由于取值均在陡變段，吸力樁周圍的土層均處在彈性階段，可以假設橫蕩約束、橫搖約束以及橫搖橫蕩耦合約束3個剛度保持不變，所以可以將這4個方程聯立求解如式（3）所示：

求解式（3），可以得到橫蕩約束、橫搖約束以及橫搖橫蕩耦合約束4個剛度如式（4）～（7）所示：

由于約束剛度矩陣是對稱陣，所以從理論上講，k24與k42得出的結果應該一致。并且浮力塔在橫搖和縱搖方向對稱，所以縱蕩、縱搖以及縱蕩縱搖耦合約束剛度與上述橫蕩、橫搖以及橫蕩橫搖耦合約束剛度一致。

首先分析k22、k44、k24和k42，依據之前的分析，F1的取值不能大于1750 kN，而M2的取值不能大于12 000 kN·m，考慮到即使土彈簧未進入過渡段，其剛度也存在著非線性，即周圍土層存在著塑性變化，并且考慮到實際運動的情況，平臺運動最大值的出現頻率并不高，所以用1750 kN 與12 000 kN·m來取土彈簧剛度并不合適，進而取上述值約60%左右即F1=1000 kN，M2=8000 kN·m 時的數據，進行土彈簧剛度分析。在圖5至圖8曲線中取值如表3所示，由式（4）至式（7）求得各約束剛度如表4所示，可以看出橫蕩橫搖的耦合剛度k24與橫搖橫蕩的耦合剛度k42偏差極小，兩者距其平均值相差0.867%，這也驗證了k24與k42的結果應該一致的結論。兩者細微的差別是由于土的非線性程度造成的，由于取值均在陡變段，并且F1與M2取值均處于曲線陡變段的中部，對應土塑性變形所占總變形的成分接近，所以k24與k42偏差極小，這也驗證了表3取值的合理性。

表3 剛度計算取值Tab.3 Values for calculation of stiffness of soil springs

表4 剛度計算結果（kN/m）Tab.4 Results of stiffness of soil springs (kN/m)

然后分析k33，依據之前的分析，Fz的取值不能大于8000 kN，同上所述，取Fz=6000 kN，在圖4 曲線中取值如表3所示，由k=Z/Fz可直接求得剛度k33，如表4所示。

將如上剛度代入式（1）并基于HydroStar 進行運動模擬，典型的橫搖RAO 如圖9 所示，縱搖的RAO 與橫搖一致。將CX-15 所在海域百年一遇的波浪條件Hs=3.8 m 和Tz=20 s 結合橫搖RAO 進行運動分析，得出平臺在百年一遇的波浪中搖動角度有義值為2.1°，結合圖6 與圖8 可以看出，這個運動值在吸力樁的安全范圍內。將CX-15 所在海域一年一遇的波浪條件Hs=1.5 m 和Tz=13 s 結合橫搖RAO 進行運動分析，得出平臺運動平均值為0.42°，有義值為0.67°，極大值為1.29°，其中遭遇一年一遇波浪的情況下，平臺運動譜分析平均值與表5所示的平臺實際運營的觀測結果基本吻合（橫搖計算值為0.42°，2017年10月橫搖實測值為0.47°）。

圖9 CX-15橫搖RAOFig.9 Roll RAO of CX-15 platform

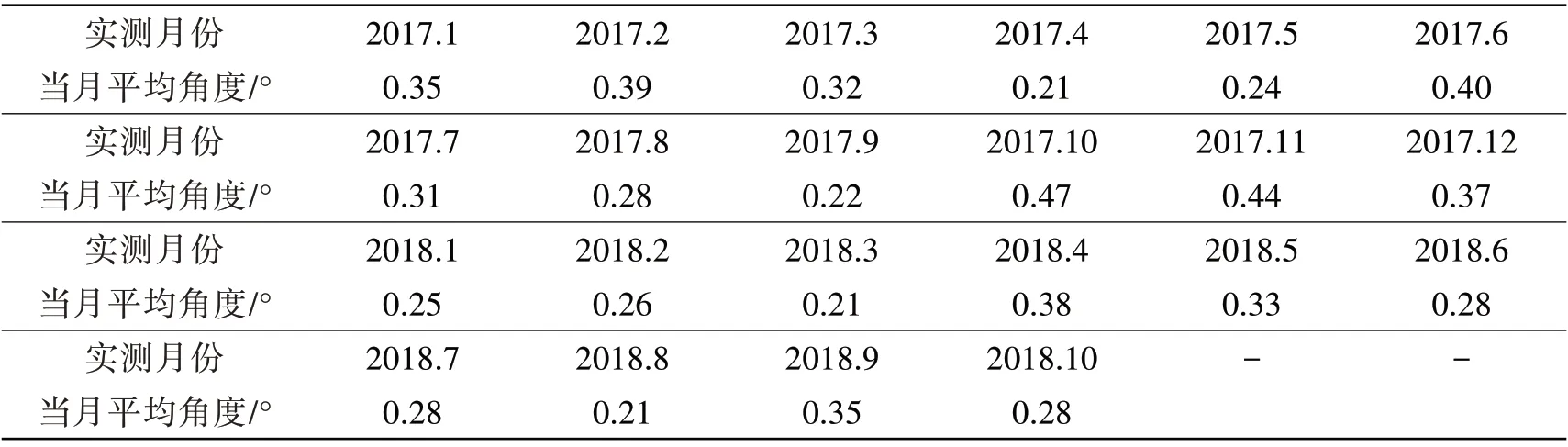
表5 浮力塔平臺CX-15在2017～2018年運動實測結果Tab.5 Rolling results of first buoyant tower CX-15 in 2017-2018

4 結 論

本文以首制浮力塔平臺CX-15為研究背景，研究了平臺吸力樁的承載力以及對平臺的運動約束。基于現場海域的土壤取樣，通過三軸壓縮試驗獲得土樣的參數；選取修正劍橋模型為土的本構模型，通過Abaqus 進行三維模擬得出了吸力樁的承載力曲線，并將承載曲線轉化為土彈簧的約束剛度，并基于該約束剛度通過HydroStar進行浮力塔的運動分析，得出如下結論：

（1）浮力塔吸力樁承載力的分析要充分結合運動的實際情況，分析工況包括升沉運動下的承載力和橫蕩橫搖耦合運動下的承載力，對比CX-15平臺現場觀測結果與P-S曲線可以看出，浮力塔吸力樁在安全的范圍內工作；

（2）通過P-S曲線可以獲得土層對吸力樁的約束剛度，約束剛度的分析需基于曲線的陡變段，該階段土層處于彈性階段，分析的結果中土的非線性效應不大；

（3）基于約束剛度矩陣進行運動分析，從結果可以看出，浮力塔在百年一遇的波浪下吸力樁也能在安全的范圍內工作，并且預報的結果與CX-15平臺現場觀測的結果吻合度較高，說明該約束剛度矩陣是合理的。