基于Maklink路徑規劃混合定位算法研究*

楊俊磊, 段倩倩

(上海工程技術大學 電子電氣工程學院, 上海 201620)

0 引 言

路徑規劃是平面上從源點出發經若干節點到達目標終點求最短路的優化問題。在路徑規劃中,常用算法分為全局和局部兩種，其中,全局路徑規劃算法有Dijkstra算法、A*算法、粒子群算法、蟻群算法等[1～4]。機器人無碰撞避開障礙物的路徑規劃是當前學者研究的熱點問題之一，研究學者常用柵格法作為機器人路徑規劃的地圖模型，不能較好體現實際地形的復雜多樣性。

目前，路徑規劃廣泛應用于工廠物資輸送，應急車輛避障救援等，這些問題不僅要保證行駛路徑最優，時間短，配送效率高，還需要規避障礙物[5,6]。何成偉等人應用Maklink圖構建無向網絡障礙物模型，保證規劃的自動導引車(automatic guided vehicle,AGV)路徑沿著凸多邊形邊緣行走不會與真實的障礙產生碰撞，但實驗研究較為單一，不能體現復雜障礙物環境的多樣性[7]。王飛等人利用Graham算法生成凸多邊形并向外擴展h的安全距離，確保飛機航線不與障礙物發生碰撞，但航線路徑需要遍歷所有節點，增加了搜索時間，規劃路徑非全局最優[8]。粒子群算法、蟻群算法等[9，10]具有良好的尋優能力、算法精度高、收斂快等優點，廣泛應用于路徑規劃問題中，并通過迭代尋找最優解。其中，粒子群算法通過適應度函數評價路徑解，但算法容易陷入早熟，局部尋優解較差。黃超等人[11]通過融合蝗蟲算法的粒子群算法改善收斂速度。文獻[1]采用廣度優先法對遍歷節點進行擴展并選出距源點最近節點作為擴展節點，但隨著遍歷節點增多，Open表節點排序時間消耗較大，計算效率較低。文獻[12]通過無線傳感器節點定位算法對錨節點精確定位，繼續擴展未知節點，定位過程中，盲節點定義為所需定位的未知節點。

針對上述學者研究成果及存在的不足，本文提出了一種混合節點定位算法(hybrid node localization algorithm,HNLA)，在不同規模地圖環境中有效減少了遍歷節點及迭代次數，節省了搜索時間并規劃出最短路徑。

1 相關工作介紹

1.1 粒子群算法

粒子群算法是Kennedy J和Eberhart R在1995年根據群鳥和魚群的成群性質提出的一種啟發式算法[13]。粒子群提供搜索算法的初始種群，粒子會隨時間改變它們的位置，并在優化系統中根據經驗選擇最佳位置Pi，全局最佳位置Pg以及搜索速度Vi。粒子速度更新根據Vid=w×Vid+c1×r1×(Pid-Xid)+c2×r2×(Pgd-Xgd)，其中，w表示慣性權重；c1和c2為常數，r1和r2為隨機函數，其值都∈(0,1)；粒子位置根據Xid=Xid+Vid更新，Xid表示粒子i在d維搜索位置。

1.2 蟻群算法

蟻群算法[14]求解路徑規劃問題主要根據信息素濃度更新以增強蟻群信息素的濃度值，提高收斂速度。通過輪盤賭法并根據概率公式(1)判斷并選擇下一節點

(1)

式中α為訪問各城市節點的程度因子，β為轉移到最近城市的程度因子，τij(t)為螞蟻從節點i到j釋放的信息素濃度總量，ηij(t)=1/dij為節點間路徑期望值，dij為節點之間距離，allow為待遍歷的節點集，信息素更新如下

τij(t+1)=(1-ρ)·τij(t)+Δτij(t)

(2)

(3)

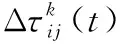
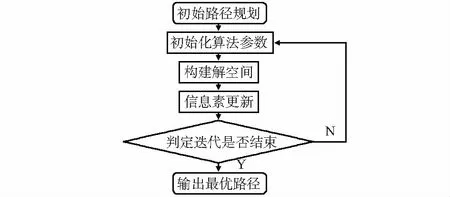
圖1 蟻群算法解決TSP流程圖

2 混合定位方法策略

2.1 區域分割

2.1.1 確定段節點

根據文獻[15]構建Maklink線規劃初始參考節點對障礙物區域進行分割,并將參考節點作為相應分割區域的段節點。圖2為初始段節點及分割區域，其中,V1，V2，…,V7為初始段節點。

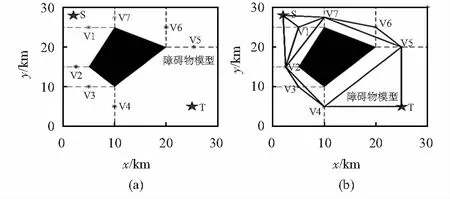
圖2 初始段節點及分割區域

2.1.2 區域分割

通過確定的段節點進行路徑搜索，將區域進一步分割：

Step1 將初始節點坐標S作為搜尋盲節點的質心坐標(xn,yn)。

Step2 由式(4)確定同段區域距離質心最遠的盲節點Am作為分割區域的搜索節點，式(5)確定第g段盲節點區域

(4)

(5)

式中m為盲節點數，dAm,Aj和dAm,Ai為Am與鄰近盲節點Aj距離及Am同其他盲節點Ai距離。若dAm,Aj≤dAm,Ai，將節點Aj加入到Am，作為段節點新的搜索位置;反之，繼續區域分割。

Step3 盲節點位置確定：1)在每次區域所分割的段中計算出已知節點到不同段中段節點的距離以及與同段中其它節點的距離;2)計算不同段中節點之間的最小距離差

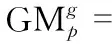
(6)

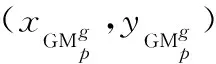
Step4 直到所有段節點區域分割完畢，停止。

2.2 盲節點邊界定位

根據先前步驟計算得到的段節點，確定盲節點位置邊界。應用文獻[16]包圍盒技術的方法計算矩形邊界，通過dAm,Ai和已知節點位置(xAi,yAi)計算矩形邊界，如圖3所示。由已知段節點Am,A2,A3及dAm,Ai,dAm,Aj確定盲節點所在位置，根據式(7)和式(8)計算盲節點位置的邊界框Ei以及邊界框的相交面積Sj

Ei=[xAi-dAm,Ai,xAi+dAm,Ai]×

[yAi-dAm,Aj,yAi+dAm,Ai]

(7)

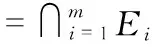
(8)

式中 矩形區域中心坐標為(xSi,ySi)，長為dAm,Ai×(1-sinθ),寬為dAm,Ai-dAm,Ajsinφ,m為盲節點數，其中,1≤i≤m。

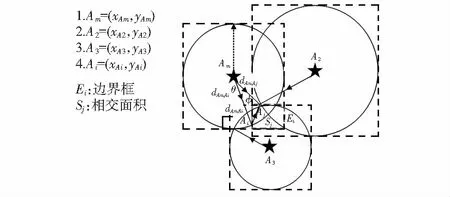
圖3 盲節點邊界定位

2.3 混合算法設計

為確保盲節點定位正確性和計算速度，使其預計位置接近最短路徑上的實際位置，本文采用粒子群和蟻群相結合的混合動態算法規劃路徑。通過最佳節點所在位置pbk,每段最佳節點所在位置plS,全局所在最優位置gb來提高搜尋速度并對盲節點定位。根據式(9)適應度值作為距離和算法收斂速度的衡量標準

(9)

式中 (xAi,yAi)為節點Ai位置；dAm,Aj為節點Am到不同區域段中盲節點Aj的距離；m為節點數量。第k只螞蟻的搜索位置和速度根據式(10)、式(11)求解

vk(t+1)=w(t)vk(t)+c1r1(pbk-xk(t))+

c2r2(gb-xk(t))+c3r3(pls-xk(t))

(10)

xk(t+1)=xk(t)+vk(t+1)

(11)

(12)

式中w=0.7，c1=c2=c3=1.494，ri∈[0,1],Lup和Ldown為從邊界框中獲得的局部化區域邊界，t為螞蟻所在最佳位置的不變時間，t′ 為區域邊界更新時間。采用粒子群算法提高搜索速度，搜索最佳節點位置，計算當前段最短路徑節點之間長度Lij，根據式(2)更新該條路徑上節點信息素

(13)

根據式(1)計算Pij，找出最優遍歷節點，迭代完成后，規劃出最短路徑L*。改進算法流程如圖4所示。

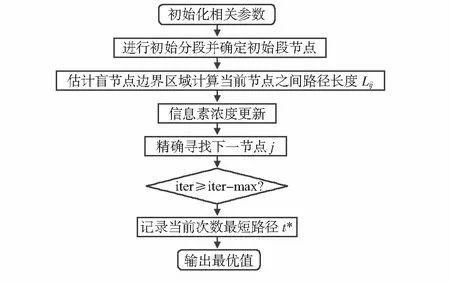
圖4 改進算法流程圖

3 實驗仿真與分析

為了驗證改進算法的有效性，在實驗平臺為Intel?CoreTMi5—4210U CPU@2.40GHz，4.00GB RAM，軟件環境為 Windows 10專業版，MATLAB2016a中編程實現對文獻[1，7]和改進算法路徑規劃，實驗模擬真實避障環境，對比分析了路徑長度、擴展節點、搜索時間以及迭代次數。

3.1 實驗仿真

構建實驗區面積為50 km×50 km，100 km×100 km,200 km×200 km的不同規模障礙物空間。目標起點分別為S1(5,10)km，S2(10,90)km，S3(20,180)km對應目標終點T1(45,45)km，T2(90,15)km，T3(160，90)km，尋找一條從起點S到終點T的最優路徑。蟻群算法相關參數設置，螞蟻個數為35，信息素因子α為1.6，啟發式因子β為5，揮發因子ρ為0.2，信息素總量Q為50，最大迭代次數為NC=500。基于上述參數設置，采用Maklink圖構建段節點，進行初始區域分割，劃分段節點以及定位節點，如圖5所示。

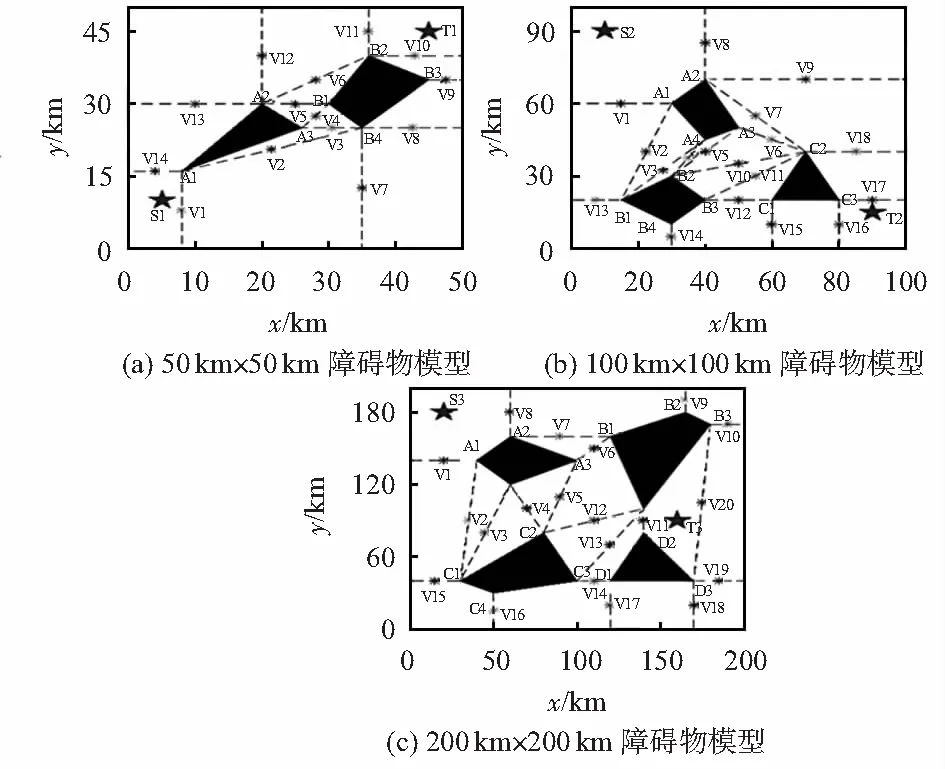
圖5 初始區域分割

3.2 實驗結果分析

通過實驗研究，隨著障礙物模型增加，路徑復雜度增加，相應分割區域、段節點隨之增加。圖6和圖7為文獻[1]、文獻[7]和改進算法路徑規劃結果以及在不同規模下迭代次數與適應度值變化曲線。

圖6(b)中點劃線為改進算法優化路徑，實線為文獻[1]算法優化路徑，虛線為文獻[7]算法優化路徑，三種算法實驗結果對比見表1。從圖6(b)及表1得出，在不同規模障礙物下，改進算法收斂速度比文獻[1]、文獻[7]算法都快，規劃路徑長度最短；采用文獻[2]路徑比的方法衡量三種算法路徑規劃的效率，實驗表明，改進算法在規避障礙物上搜索全局路徑效果比其他兩種算法路徑更優。

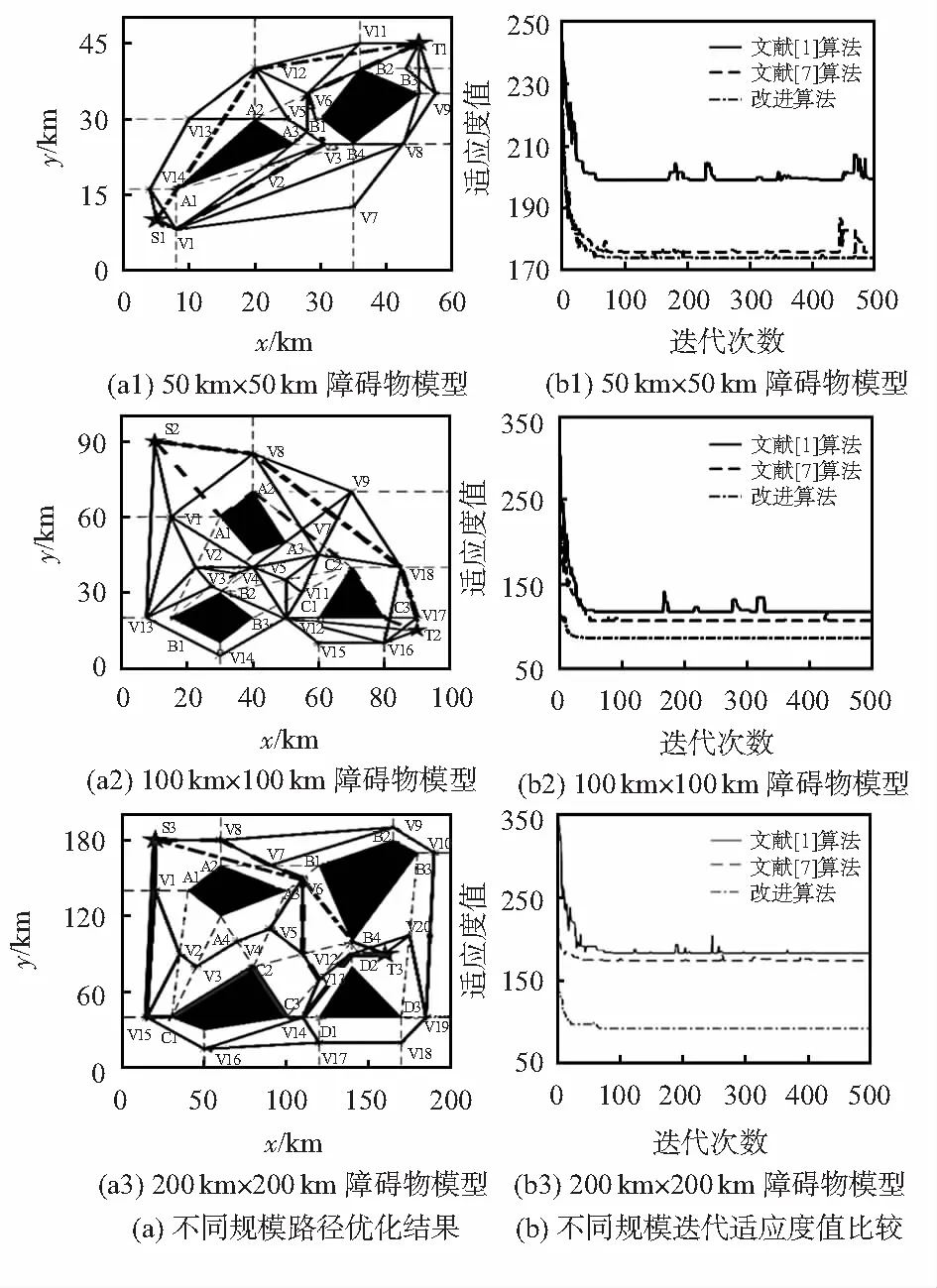
圖6 實驗結果

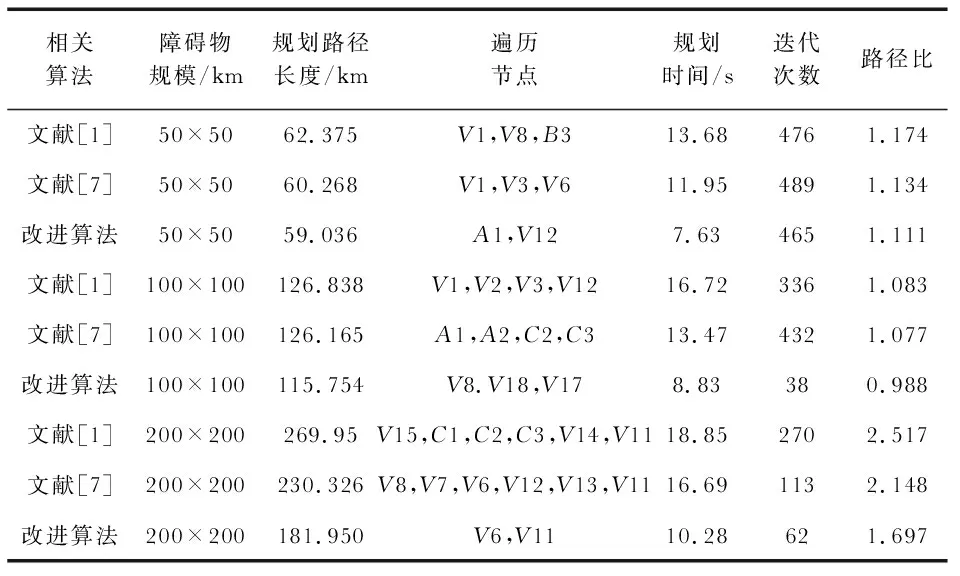
表1 實驗結果對比

4 結束語

隨著路徑規劃障礙物規模增大，文獻[1]和文獻[7]算法在問題解精度以及收斂速度上存在不足。提出加快搜索速度、精確節點定位的改進算法，對節點所在位置精確估計，求解最優路徑。實驗結果表明：改進算法的最優解精度以及收斂速度優于其他兩種算法，當障礙物規模、復雜度增大時，改進算法節點定位的有效性更加突出。在后續研究中，將在不同規模障礙物的三維環境下，研究改進算法的求解精度以及收斂性。