分數階微積分在滑模控制中的應用研究*

張 鑫， 魯文儒， 繆仲翠， 姜子運， 徐文波

(1.蘭州交通大學 自動化與電氣工程學院，甘肅 蘭州 730070；2.甘肅省人工智能與圖形圖像處理工程研究中心,甘肅 蘭州 730070)

0 引 言

滑模控制的特點是在其設計過程中不需要系統提供十分精確的動力學模型，只需要利用軌跡的跟蹤誤差或者位置控制誤差合理設計滑模面即可，并擁有響應快、魯棒性好等特點，這種方法在此類非線性、不確定性的系統中應用十分廣泛[1～4]。滑模控制的設計主要包括滑模面和趨近律的設計，其中趨近律的設計問題一直備受關注。

趨近運動作為滑模運動中的一大重要組成部分，其過程是指系統由任意的初始位置向切換面趨近，最終得以到達切換面的一種運動形式。能夠合理選用趨近律，可以加快趨近的速度、減少系統抖振。在傳統的滑模控制理論當中，十分常用的趨近律主要是等速趨近律、指數趨近律等[5]。

不同于整數階微積分理論，分數階微積分的階次是能夠任意選取的，從而大大提升了控制系統設計過程中的靈活度[6]。近年來，許多學者將分數階微積分與滑模控制相結合，形成分數階滑模控制[7]。 其中，文獻[8]以一類不確定性系統為研究對象，提出了一種基于分數階微積分理論的滑模控制方法，并在磁軸承系統和陀螺儀系統上進行了驗證。文獻[9]以永磁同步電機為研究對象，提出一種參數自整定的分數階滑模控制方法。文獻[10]以永磁同步電機為研究對象，針對其位置控制，提出一種分數階滑模控制器。文獻[11]將分數階滑模控制策略應用于一種撓性航天器上，以此實現對航天器姿態跟蹤問題的解決，并取得了較好的效果。文獻[12]則在直流調速系統中使用一種改進型的分數階滑模控制方法，以此實現對直流調速系統動態性能的改善，達到減小抖振的效果。但是以上文獻均沒有從數學角度來充分證明分數階微積分與滑模控制相結合后的趨近問題以及滑模控制所存在的抖振現象。

本文利用分數階微積分與滑模控制提出分數階滑模趨近律，重點從數學角度分析了分數階趨近律的趨近速度問題以及滑模控制所存在的抖振現象，并且通過仿真實驗證明的所提出分數階趨近律的有效性和穩定性。

1 分數階趨近律設計

目前，在控制領域中應用較多的分數階微積分定義有三種，分別為：Grunwald-Liouvile(GL)定義、Riemann-Liouvile(RL)定義以及Caputo定義[13]。Caputo型分數階微積分初始條件的定義與整數階微積分的相一致，近年來在工程應用中得到了廣泛的研究。

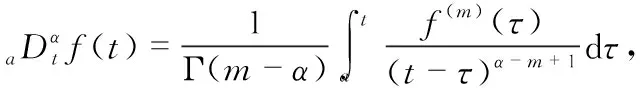
m-1<α≤m

(1)

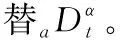
引理1[8]：已知如下系統

Dαx(t)=f(x,t)

(2)

如果x=0是該非自治分數階系統的平衡點，且f(x,t)滿足Lipschitz條件。假設存在一個Lyapunov函數V(t,x(t))滿足下列條件

α1‖x‖≤V(t,x)≤α2‖x‖,

V(t,x)≤-α3‖x‖

(3)

式中α1，α2和α3均為正常數，β∈(0,1)。則式(2)是漸近穩定的。

本文設計的分數階趨近律為

Dαs=-ksign(s)

(4)

其中,0<α<1。控制系統狀態到達滑模面速度通過改變階次α和系數k改變。

2 分數階趨近律性能分析

2.1 穩定性分析

證明：采用Lyapunov函數

(5)

根據Caputo分數階微積分定義形式(1)

(6)

對式(5)兩端進行求導，結合所選取分數階趨近律和式(6)，得

(7)

利用sign(D1-α(-ksign(s)))=-ksign(s)[14]，得

=-ksign(sT)sign(s)=-k

(8)

2.2 趨近律穩態抖振分析

以傳統指數趨近律為例

(9)

當S趨近于0時，在滑模面上的極限為

(10)

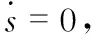
2.3 趨近速率分析

趨近速率分析：

1)指數趨近律趨近時間

由式(9)可得

(11)

當滑模面s>0時

(12)

當滑模面s<0時

(13)

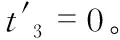
(14)

2)分數階趨近律趨近時間

為解決此問題，使用?階Riemnnan-Liouvile分數積分，然后使用標準導數。

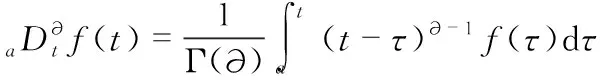
(15)

Gamma函數定義為

(16)

由文獻[15,16]得

(17)

利用s(t)-s(0)=J?(-ksign(s))簡化上式為

(18)

由式(18)得

(19)

所以分數階趨近律趨近時間為

(20)

由式(14)、式(20)可得

(21)

從上面的推導可以得出結論：分數階趨近律的趨近速度要比指數趨近律的趨近速度快。

3 仿真實驗

n關節機械臂動力學模型如下[17]

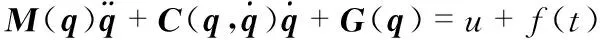
(22)

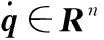
將本文所提出來的分數階趨近律與傳統指數趨近律進行對比分析，選擇滑模面為

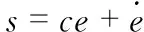
(23)

策略1指數趨近律控制律[18]

策略2分數階滑模控制律

根據機械臂動力學模型，qd(t)為關節期望位置,q(t)為關節實際位置，定義關節位置跟蹤誤差為

e(t)=qd(t)-q(t)

(24)

對式(24)求二次導為

(25)

對式(23)求一次導為

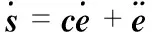
(26)

將式(22)和式(24)代入式(26)得

(27)

對式(4)求一次導為

(28)

由式(27)和式(28)得到控制律為

(29)

以兩關節機械臂為例，通過FOMCON[19]工具箱進行仿真分析。

當給定期望軌跡為單位階躍響應時，得到如下結果。圖1為三種方法下的單位階躍響應曲線，表1為三種方法下的單位階躍響應性能指標，由圖1和表1可知，本文所提方法可以較好地滿足單位階躍響應中動態性能指標與穩態性能指標的要求(當以正弦為輸入信號時)。

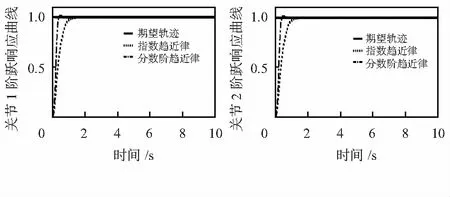
圖1 階躍響應曲線

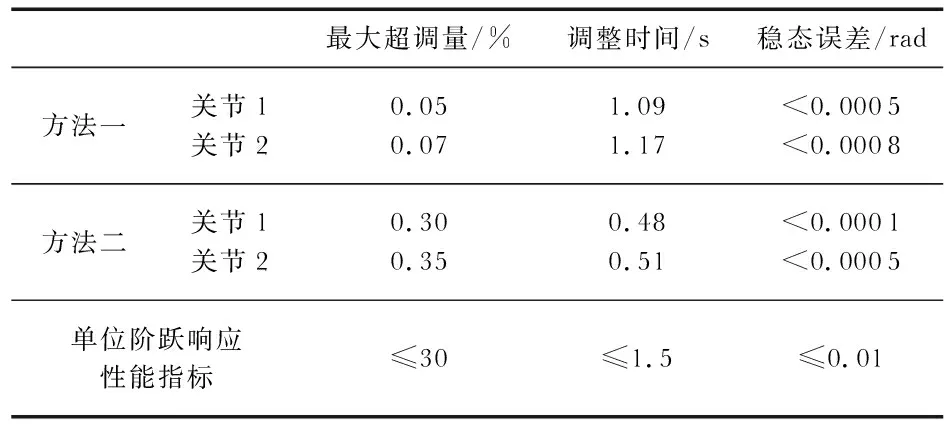
表1 單位階躍響應性能指標

圖2為機械臂兩個關節的控制輸入曲線。由圖2可得，在指數趨近律下系統抖振明顯，即本文所提出的分數階趨近律可以使機械臂運行更加平滑穩定，很大程度上削弱了抖振。

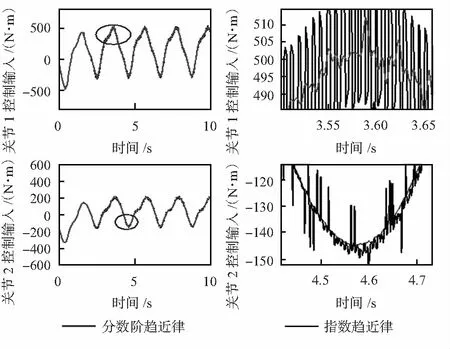
圖2 控制輸入曲線

圖3為在兩種趨近律下兩個關節的位置跟蹤曲線。由圖3可知，在分數階趨近律下兩個關節的位置跟蹤效果更好，跟蹤速率更快，控制精度更高。

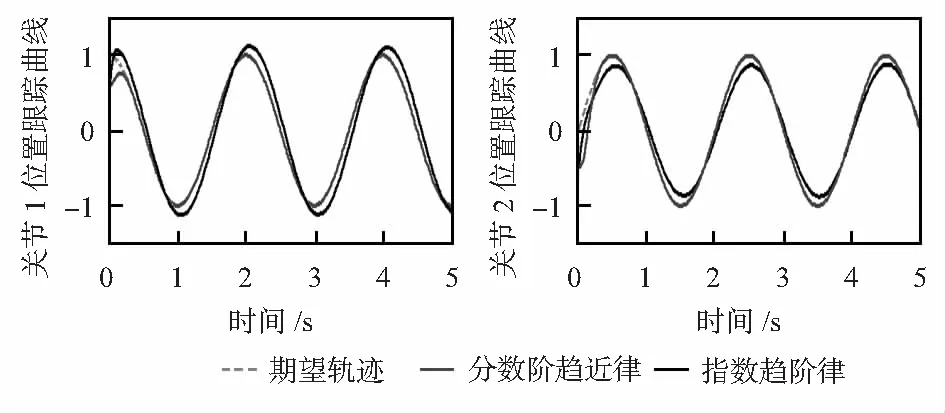
圖3 位置跟蹤曲線

圖4為位置跟蹤誤差曲線，選取角位移調整時間與位置誤差的均方根誤差作為判斷參考值，所得數據比較結果如表2所示。

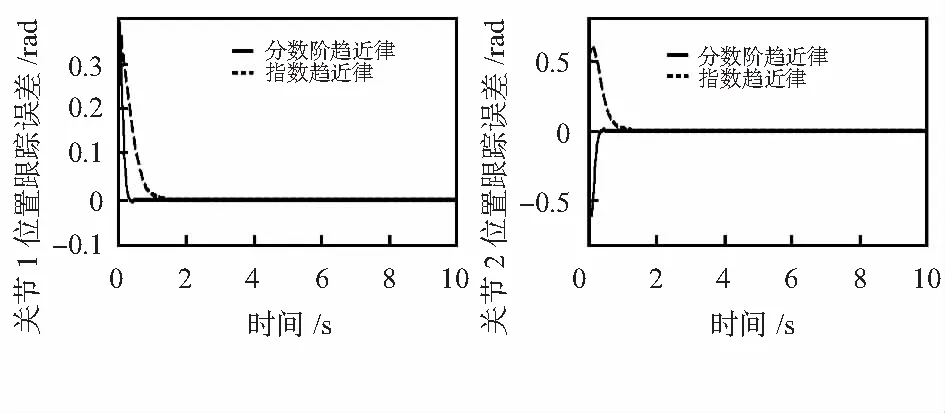
圖4 位置跟蹤誤差曲線

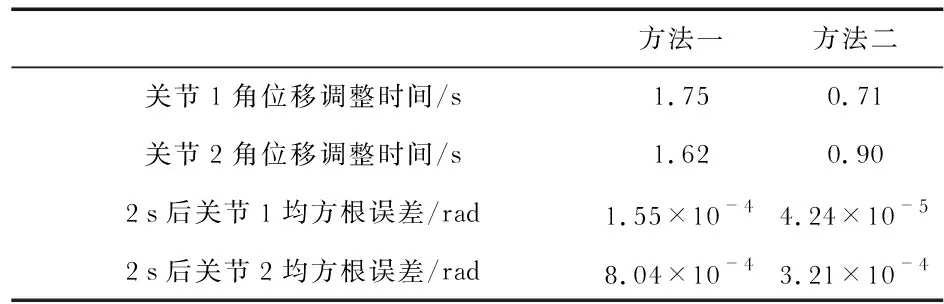
表2 控制方法數據比較

為了進一步驗證在分數階趨近律下系統的抗干擾能力，引入干擾

f(t)=200×exp(-(t-3)2/(2×0.12))

(30)

式中 200為干擾峰值，3為干擾中心位置，0.1為干擾時間寬度。仿真得到如圖5的位置跟蹤誤差曲線。由圖5可得，分數階微積分的引入可以增強系統的魯棒性。

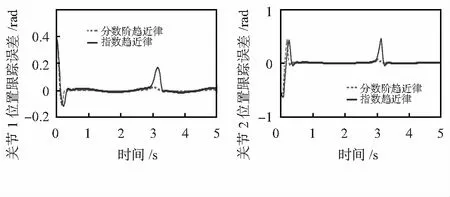
圖5 干擾下的位置跟蹤誤差曲線

4 結 論

本文首先介紹了分數階微積分的相關定義，然后以機械臂為研究對象，把分數階微積分與滑模控制相結合，提出一種分數階趨近律，并利用仿真實驗與指數趨近律進行了對比分析，得到如下結論：

1)分數階趨近律的引入主要表現在能夠柔化運動軌跡，具有更優良的平滑特性，同時在很大程度上實現了對抖振的削弱。此外，分別在分數階趨近律以及傳統指數趨近律下關節1的角位移調整時間分別為1.75,0.71 s，關節2的角位移調整時間分別為1.62,0.90 s，同時各關節的均方根誤差也大大減小。

2)在引入干擾后在分數階趨近律下的控制器具有更好的魯棒性，系統的抗干擾能力更強。

因此，與傳統指數趨近律相比，分數階趨近律，在很大程度上使各關節的跟隨速度與跟隨效果得到增強，系統抖振明顯減小。