基于深度強化學習的分布式電驅動車輛扭矩分配策略

孔澤慧 樊杰

（1.廣西機電職業技術學院，南寧 530007；2.中國汽車工程研究院股份有限公司，重慶 401122）

主題詞：分布式驅動 電動汽車 深度強化學習 扭矩分配

1 前言

分布式驅動電動汽車（Distributed Drive Electric Vehicle，DDEV）具有響應快、加速性好、多自由度、控制靈活等獨特優勢，在提升車輛操縱穩定性、安全性和經濟性等方面極具潛力。

前、后軸扭矩分配策略是DDEV發揮上述潛力的關鍵所在，如：Nam等為提升車輛經濟性提出了面向急加速場景的車輪防滑控制策略；孟彬運用動態方法尋找輪轂電機的高效區，獲得了前、后軸扭矩分配系數；X.Yuan等提出了一種扭矩分配策略，解決了低需求扭矩下系統的低效問題。但上述方法僅面向驅動工況，未考慮DDEV 的制動能量回收。為充分發揮電驅動系統在可再生制動領域的獨特優勢，Sun 等運用非線性模型預測控制方法設計了DDEV的再生制動扭矩分配策略，J.Zhang 等綜合考慮驅動、制動場景，設計了再生制動和摩擦制動的協調控制策略。雖然上述研究將電機的制動能量回收也納入優化范疇，但扭矩分配以經濟性為目標，未考慮制動穩定性約束，存在應用局限性。

扭矩分配策略依據算法可分為基于規則和基于優化的方法。基于規則的方法因具有高可靠性而廣泛應用于實車，但應用效果受工況影響較大；基于優化的方法在變量可行域中以最小化成本函數為目標求解最優控制變量，優化效果遠優于基于規則的方法，因此日益受到重視。目前常用的優化方法包括動態規劃、粒子群算法和強化學習等。其中，強化學習作為當代前沿智能算法的一類典型代表，在控制領域已取得了令人矚目的應用成果，如何洪文等運用深度強化學習方法為功率分配型混合動力電動客車設計了能量管理策略，其燃油經濟性與基于動態規劃的全局最優結果近似度超過90%。

考慮到強化學習在控制領域的強大應用潛力，本文提出一種基于深度強化學習的DDEV前、后軸扭矩分配策略。在保證制動穩定性的前提下，以車輛的總需求扭矩和車速為狀態輸入，前、后軸扭矩分配系數為輸出，利用深度神經網絡建立狀態輸入到控制輸出的最優映射，并通過與傳統固定系數的前、后軸扭矩分配策略對比，驗證算法的有效性。

2 DDEV車輛建模

DDEV的結構如圖1所示。車輛由4個獨立的電機驅動，每個電機連接1 個離合器，并通過輪邊減速器與車輪相連。其中，、分別為質心與前、后軸的距離。

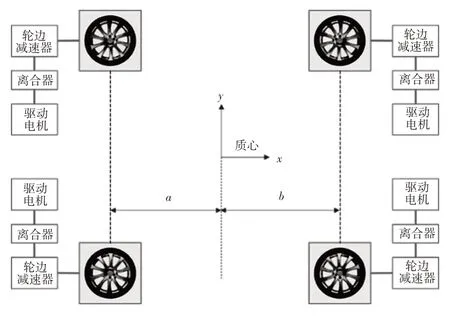
圖1 DDEV結構示意

為了求解控制策略，需要建立能夠準確模擬車輛動態響應的物理模型。本文采用商業化車輛動力學軟件CarSim內置的車輛模型，包括駕駛員模型、懸架模型、輪胎模型，其中考慮了輪胎力飽和效應、輪胎遲滯效應、輪胎載荷轉移效應等。其他車輛子系統，包括驅動電機、機械制動系統、電池模型等，對其進行數學建模，并搭建MATLAB∕Simulink模型。

2.1 電機模型

電機模型可以表示為：

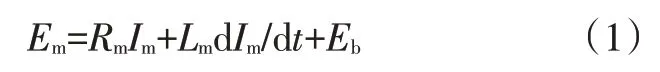
式中，、分別為電機的電壓和電流；、、分別為反電動勢、電樞電阻和電樞電感，并且：

式中，、均為電機常數，取決于電機結構、繞組數量和鐵芯材料屬性等；為電機轉速；為電機扭矩。

另外，電機的電壓和電流需要滿足：

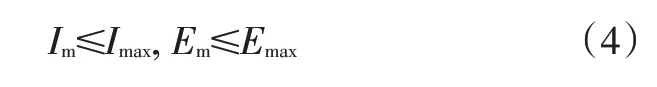
式中，、分別為電機的最大電流和最大電壓。

根據文獻[12]的測試結果，繪制如圖2 所示的電機效率MAP，為簡化計算，認為電機在制動時的效率與其在對應狀態下的驅動效率相同。

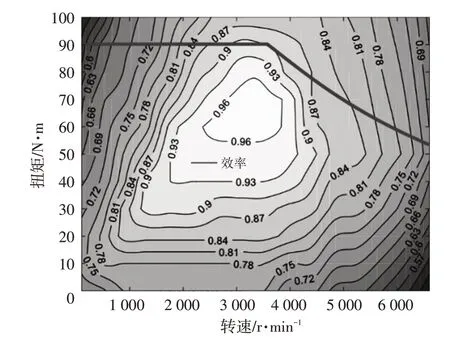
圖2 電機效率MAP

電機功率是輸出扭矩、電機轉速和電機效率的函數，可以表示為：

式中，為電機效率，可以根據圖2由電機扭矩和電機轉速插值獲得，電機扭矩和轉速可以通過電機控制器的傳感信號獲取。

2.2 機械制動模型

電機的制動力矩雖響應迅速，但十分有限，因此在大制動強度下需要機械制動系統參與制動。本文假設電制動和機械制動能夠實現制動力矩的連續調制，力矩響應可以近似為如下一階系統：

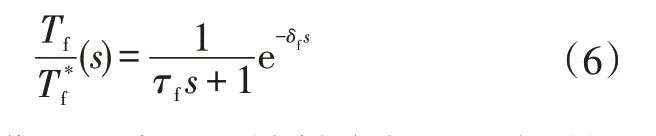
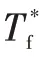
2.3 電池模型

本文采用鋰離子動力電池作為能量源，一階RC 電路電池模型為：

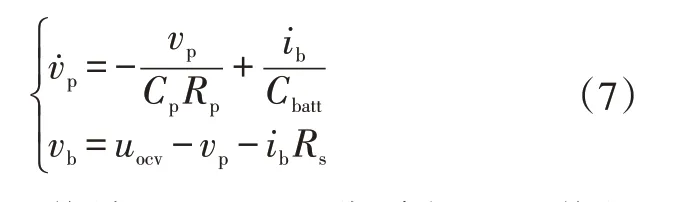
式中，為一階RC網絡端電壓；、分別為RC網絡的極化電容和極化內阻；為激勵電流；為電池容量；為電池端電壓；為電池開路電壓；為歐姆內阻。

根據安時積分規則，電池荷電狀態（State of Charge，SOC）與電池容量和激勵電流存在以下關系：

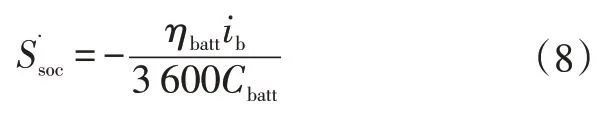
式中，、分別為電池的荷電狀態和充放電效率。

以SOC的多項式函數進行建模：

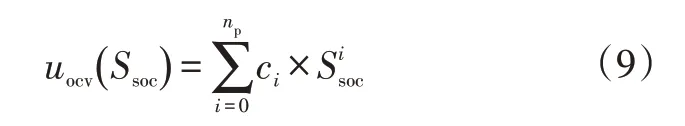
式中，c為第階SOC分量對應的多項式系數；為多項式的階數，本文取=5，即認為是的五階多項式函數。

部分整車參數如表1所示。

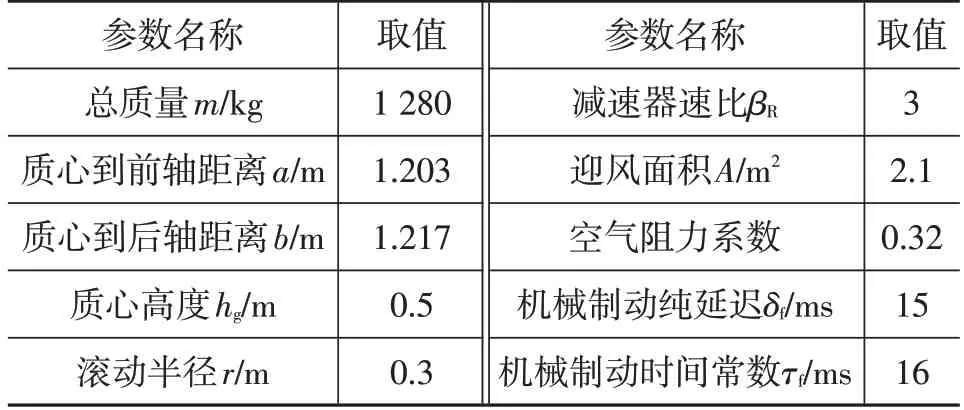
表1 車輛基本參數

3 基于深度強化學習的扭矩分配設計

強化學習的思想是通過與環境的試錯交互，基于觀測值及對系統行為的分析提高系統性能，通常以最大化累計回報函數為目標，獲得最優控制策略。

-learning 是著名的強化學習方法，當給定控制策略時，在狀態s下執行動作a時的動作值函數可以表示為：

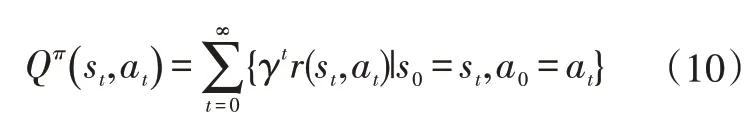
式中，為[0,1]范圍內的折扣因子，表示將未來回報折算到當前時間點的回報折算值；為單步回報；Q為動作值函數，表示在當前狀態s下，執行動作a后的長期期望累計回報。

最優動作值函數定義為：

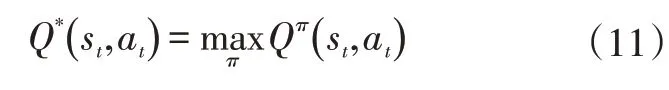
可以通過選擇最大化值的動作來獲得最優控制策略：

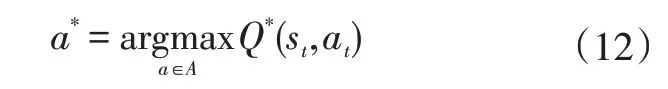
式中，為動作變量的可行域空間；為執行的動作；為獲得最優值函數的動作。

傳統的-learning 通過離散化狀態和動作參數來獲得從狀態到動作的最優控制策略，但針對DDEV扭矩分配，由于系統的狀態（需求扭矩、車速）為連續輸入，一方面，離散化會影響最終優化策略求解的精度，另一方面，過度的離散化也會帶來“維數災難”，增加運算負擔。因此，為了對包含連續狀態的控制問題應用learning，可運用深度強化學習算法，通過神經網絡實現從連續狀態到動作值函數的映射：

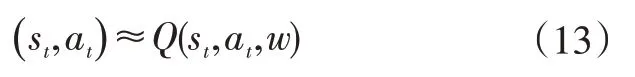
式中，為深度神經網絡的參數；(s,a,w)為從狀態s和動作a到動作值函數的映射。

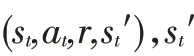
本文定義需求扭矩和電機轉速組成的二維向量為系統狀態，即=(,)，系統的動作為前、后軸的扭矩分配系數，這里定義為前軸扭矩在總驅動扭矩中的占比，并且假定同一軸上的2個電機輸出扭矩相同，即

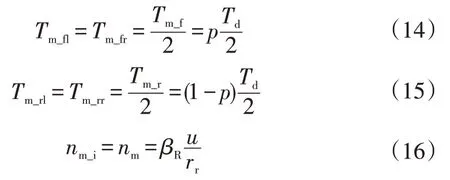
式中，、、、分別為左前輪、右前輪、左后輪、右后輪的扭矩；、分別為前、后軸的扭矩；為輪邊電機轉速；=1,2,3,4 分別表示左前、左后、右前、右后輪；為車速；為車輪的滾動半徑；為輪邊減速器的速比。

控制目標為整車的經濟性最優，由于-learning 算法通常最大化累計期望回報，而本文的優化目標是最小化瞬時能耗，因此定義瞬時回報為系統瞬時能耗的相反數：

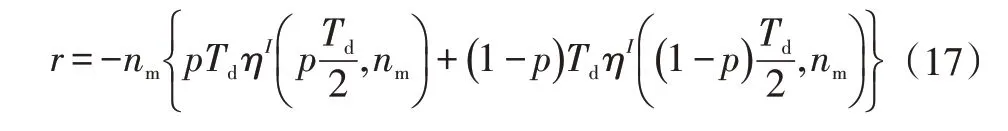
式中，為指示函數，驅動狀態時=-1，制動狀態時=1。

本文設定神經網絡具有4個隱含層，隱含層之間為全連接結構，每層擁有500 個神經元，神經元的激活函數為，輸入層有2個神經元，分別代表狀態向量中的需求扭矩和電機轉速，輸出層有11 個神經元，將在[0.5,1.0]范圍內均分為10 等份，11 個神經元依次代表取0.50、0.55、0.60、…、0.95、1.00 時對應的動作值函數。的最小值為0.5，即前軸的扭矩始終不低于后軸，原因是前驅車輛具有不足轉向特性。

另外，系統必須滿足的約束條件還包括：

式中，為輪邊電機扭矩；=1,2,3,4 分別表示左前、左后、右前、右后輪；、分別為最大扭矩和最大轉速。

當車輛處于制動狀態時，還需要滿足制動穩定性約束。理論上，為了達到最大制動效能，前、后軸應同時達到“抱死”條件，此時前、后制動力和滿足圖3所示的I曲線，即

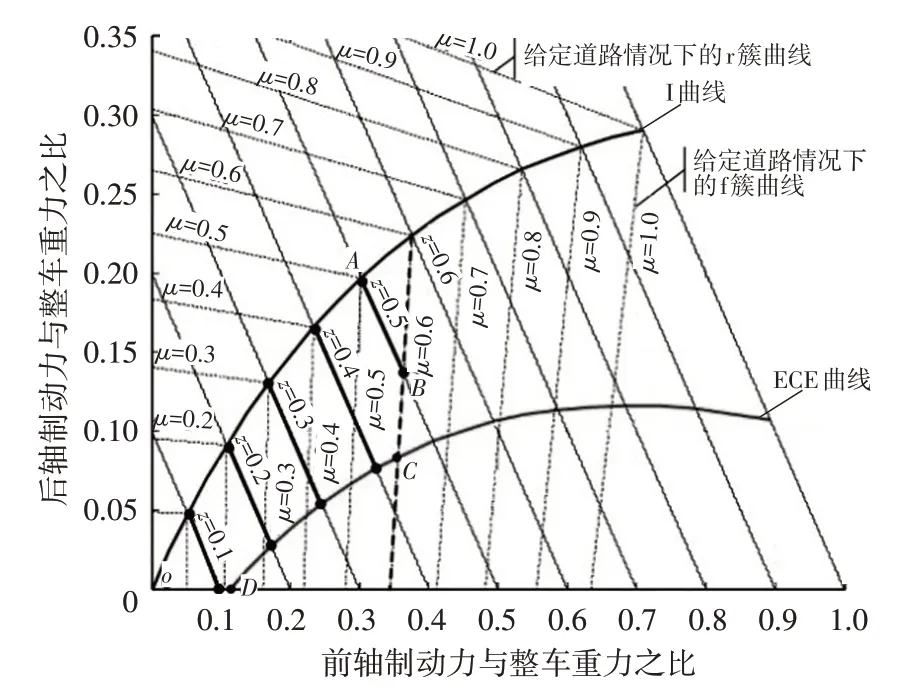
圖3 制動穩定性邊界

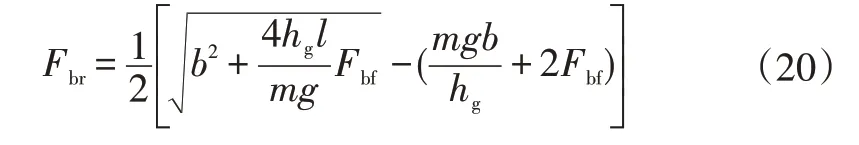
式中，為車輛質心高度；為軸距。

然而，實際情況下很難實現前、后軸同時達到“抱死”，為保證車輛的穩定性，通常允許前軸較后軸先抱死，即前、后制動力分配系數應該在I曲線下方。

另外，歐洲經濟委員會（Economic Commission for Europe）規定了后軸最小制動力以避免前軸過于容易達到“抱死”且保證制動距離滿足要求。根據規定，制動強度和路面附著系數應滿足：

因此，可以得到如圖3所示的ECE曲線，其表達式為：

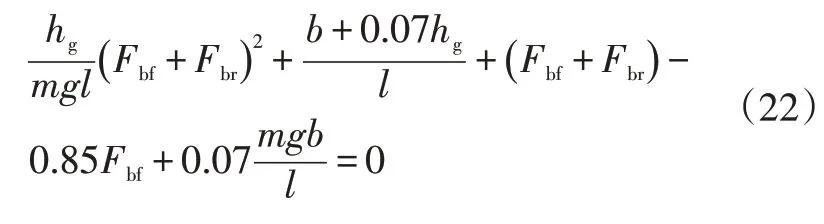
另外，美國州公路工作者協會研究表明，在緊急情況下，良好路面上的制動強度可達0.55，而一般情況下的制動強度通常低于0.35。因此，本文將制動強度限定在0～0.5范圍內。如果制動強度超過0.5，將被認為是緊急制動，為保證制動的可靠性，可完全采用機械制動。

根據上述分析，從制動穩定性角度看，的可行域為圖3中圍成的區域。

本文采用的深度強化學習相關網絡參數如表2 所示，詳細算法流程為：

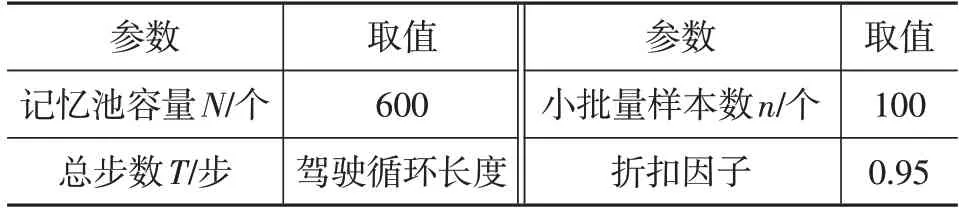
表2 深度強化學習參數

基于深度強化學習的DDEV 扭矩分配計算流程如圖4所示。

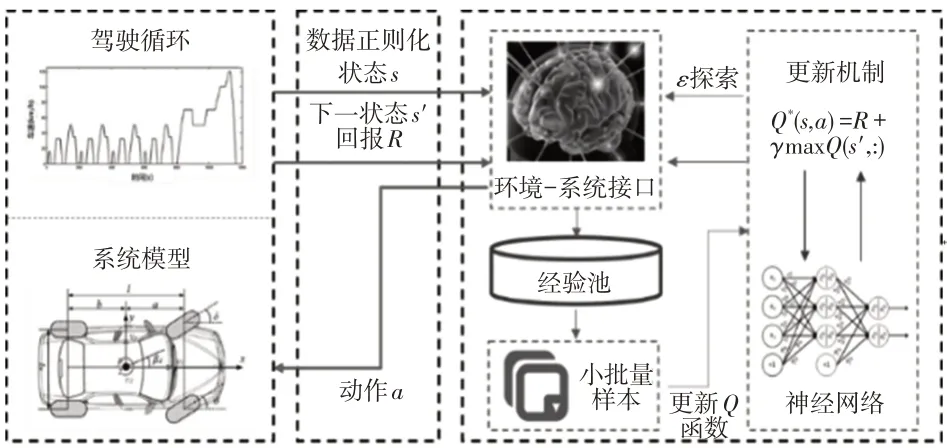
圖4 基于深度強化學習的DDEV扭矩分配計算流程

4 仿真結果及討論

4.1 NEDC工況試驗仿真

新歐洲駕駛循環（New European Driving Cycle，NEDC）工況下，基于深度強化學習求解的驅動和制動狀態下的最優扭矩分配MAP 如圖5 所示：當需求扭矩（絕對值）較低時，為了避免電機在低扭矩情況下進入低效區，通過前軸電機產生驅動力或進行制動能量回收；當需求扭矩較高時，扭矩近似在前、后軸間均等分配。

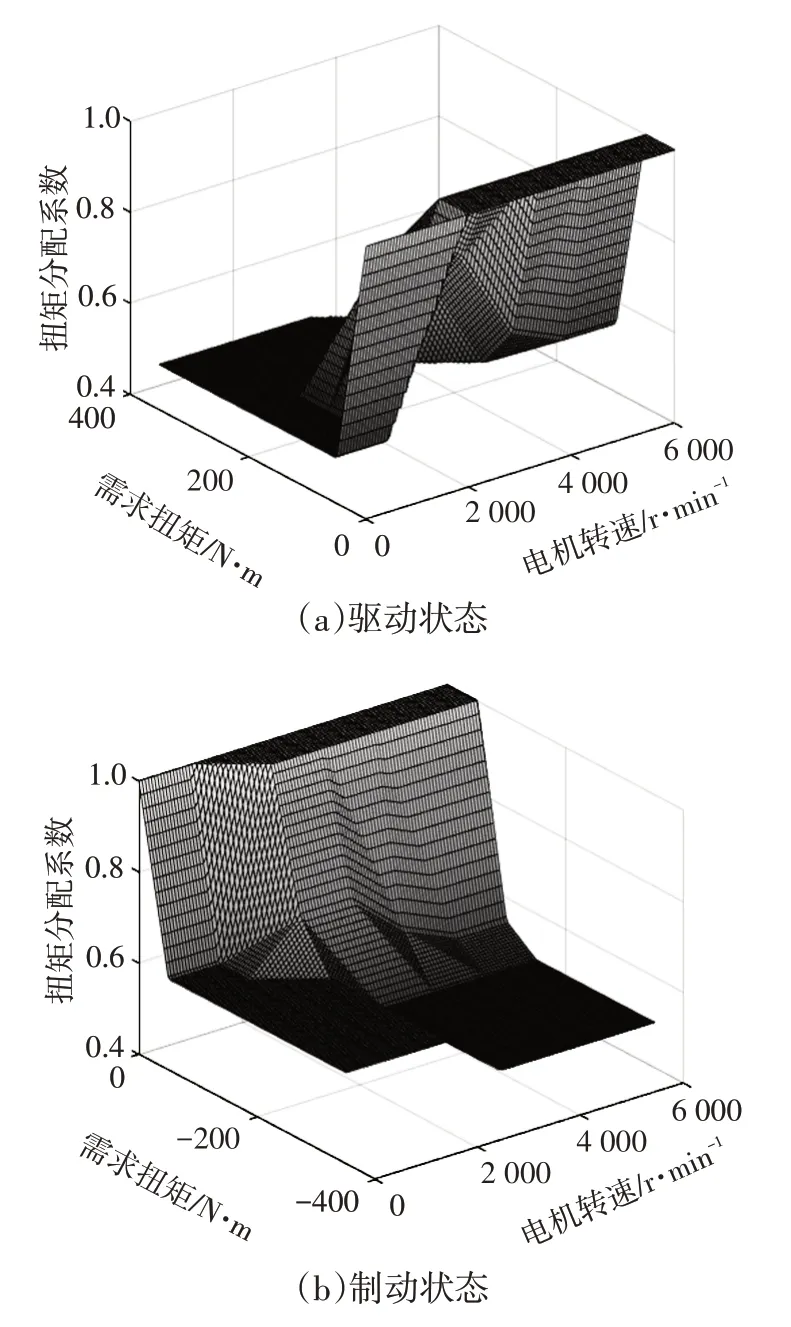
圖5 基于深度強化學習求解的最優扭矩分配MAP

為了驗證所提出的基于深度強化學習的DDEV 扭矩分配策略的經濟性優勢，采用傳統扭矩分配策略作為對比基準。傳統扭矩分配策略在驅動狀態下，力矩在4 個車輪間通常平均分配，在制動狀態下，制動力在前、后軸間按照固定比分配。為了保證車輛的制動穩定性，一般要求車輛的前輪制動力稍大于后輪制動力，取=0.6。制動時優先采用再生制動，如果電機制動力矩能夠滿足制動需求，則完全由電機制動，否則，電機按照最大力矩進行制動，所需的剩余制動力由機械制動補足。

通過CarSim 和MATLAB∕Simulink 聯合進行NEDC工況仿真，為了量化對比，引入以下指標：

a.牽引效率，用于評價驅動系統的能耗水平：

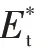
b.再生制動率，用于評價再生制動系統的能量回收能力：

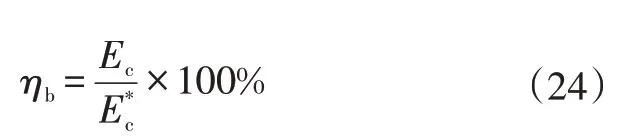
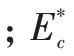
c.節能率，用于評價整車的節能水平：

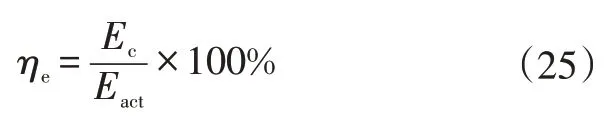
式中，=-。

在如圖6所示的NEDC工況下分別進行2種控制策略的仿真。設定電池初始SOC 為80%，2 種扭矩分配策略下的電機扭矩輸出和驅動∕制動功率對比如圖7所示，可以看出：在NEDC的市區工況下，2種控制策略的輸出基本一致；在高速、市郊工況下，由圖7a和圖7b可知，基于深度強化學習的控制策略更傾向于使用前軸驅動；圖7d表明，基于深度強化學習的扭矩分配可節省超過10%的驅動功率，同時制動回收功率可增加近10%。

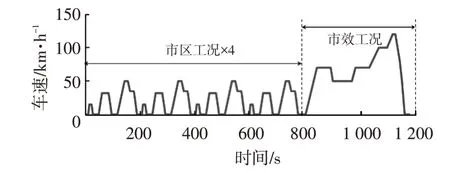
圖6 NEDC工況

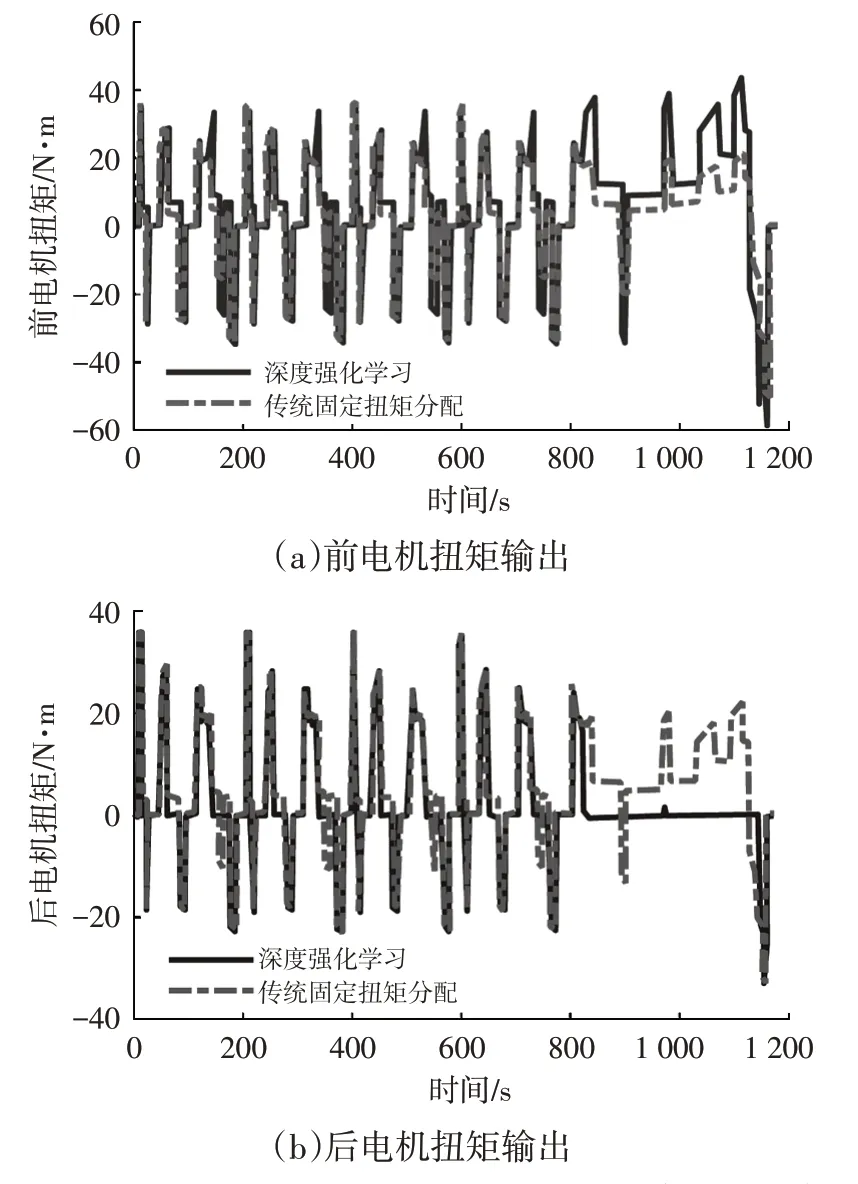
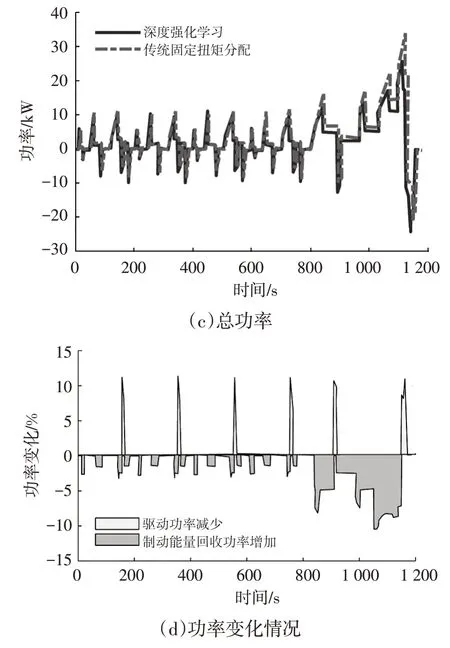
圖7 2種扭矩分配策略結果的對比

表3和表4分別對比了2種控制策略的能耗特性和評價參數。與傳統方法相比，深度強化學習策略對應的牽引效率和再生制動率均有所提高，其中牽引效率提高了4.18百分點，再生制動率提高了4.92百分點。除此之外，2種策略下初始SOC均設定為80%，在結束時，強化學習對應的SOC比傳統策略高出3.96百分點。由于上述在驅動和制動工況下的改善，車輛節能率提高了3.48百分點。

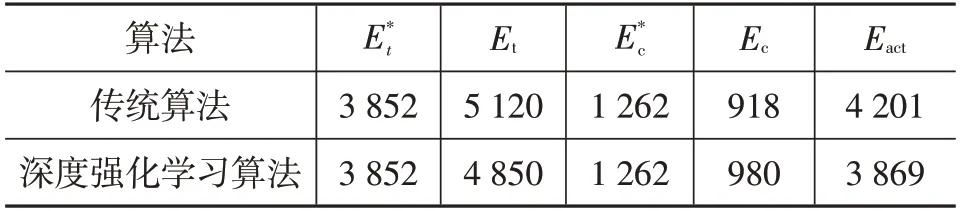
表3 能耗特性對比 kJ

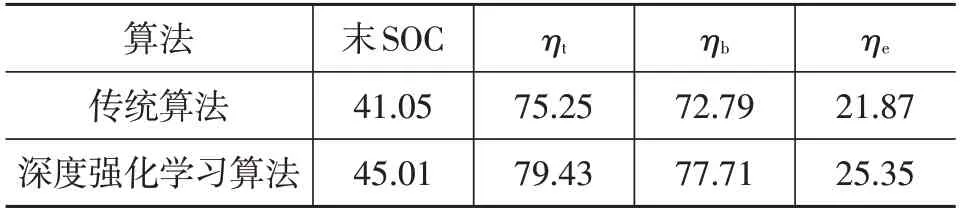
表4 評價參數對比 %

4.2 對開路面大強度制動硬件在環測試

為了驗證所提出的控制策略能否保證車輛良好的制動穩定性，通過硬件在環測試進行對開路面大強度制動測試，對開路面左、右側附著系數分別設定為0.2 和0.5，制動強度取0.5（即所提出控制策略允許的制動強度上限值）。基于RT-LAB和MotoTron的硬件在環仿真測試平臺如圖8 所示，在該平臺中，基于深度學習算法獲得制動扭矩分配MAP并作為扭矩分配原則，MotoTron控制器接受需求扭矩和電機轉速信號，根據制動扭矩分配MAP 插值獲得扭矩分配系數，RT-LAB 中包含分布式車輛的系統模型，接受MotoTron控制器發送的扭矩分配信號，同時輸出需求扭矩和電機轉速。

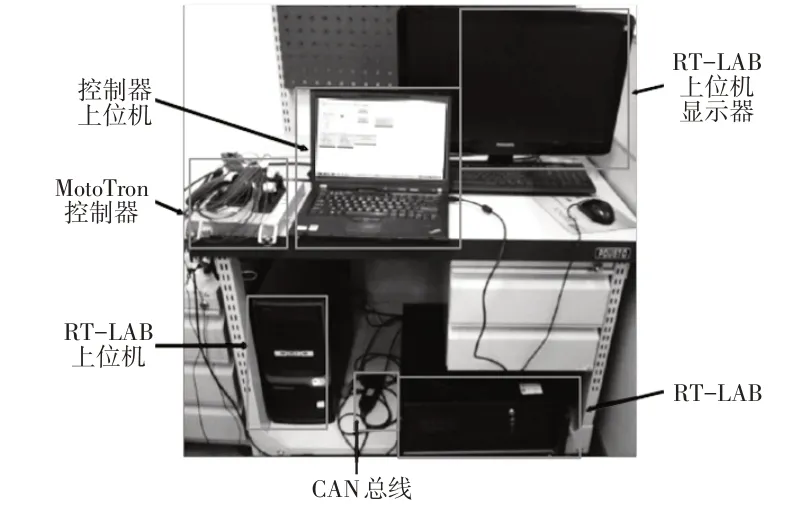
圖8 基于RT-LAB和MotoTron的硬件在環測試平臺

傳統策略和基于深度強化學習的策略下4 個車輪的滑移率如圖9 所示，可以看出：對于傳統扭矩分配策略，在施加制動信號后，左側車輪先后進入低附著系數路面，滑移率迅速提高，最高可達到4%左右，由于車輛在高滑移率時，附著率較低，導致路面可對左側車輪提供的最大附著力降低，從而使整車左側處于易打滑狀態，而右側車輪處于低附著良好狀態，左、右側附著力的不平衡使車輛處于不穩定狀態；而本文提出的控制策略，由于增加了制動穩定性約束，左側車輪的滑移率一直控制在20%附近，此時車輪具有較為理想的附著特性，車輛的穩定性良好。

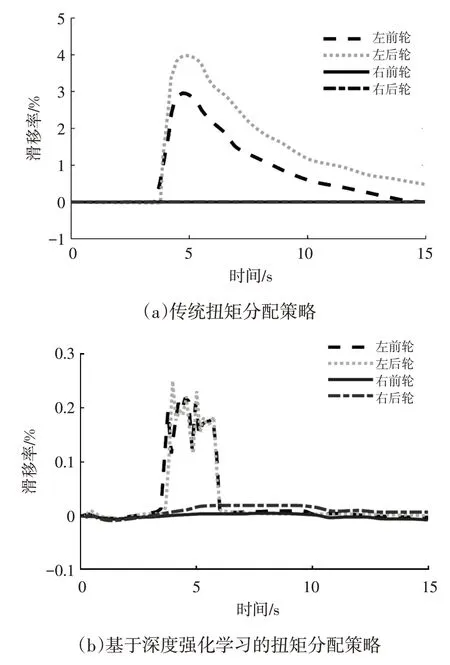
圖9 2種扭矩分配策略滑移率的對比

5 結束語

本文面向分布式驅動車輛，提出了基于深度強化學習的扭矩分配策略，在保證車輛制動穩定性的前提下，以經濟性為目標，獲得了前、后軸扭矩的最優分配系數。驗證結果表明：在NEDC 工況下，相比于傳統的固定前、后軸扭矩比的控制策略，提出的控制策略可以實現牽引效率和再生制動率的提高，節能率提高了3.48百分點；在對開路面大強度制動硬件在環測試中，所提出的控制策略能夠將低附著系數路面車輪滑移率控制在20%附近，保證了車輛的制動穩定性。