基于遺忘遞推最小二乘與自適應無跡卡爾曼濾波的鋰電池SOC估計*

劉鵬 李云伍 梁新成

（西南大學，重慶 400715）

主題詞：鋰電池 荷電狀態 等效電路模型 無跡卡爾曼濾波

1 前言

鋰電池荷電狀態（State of Charge，SOC）是電動汽車電池管理系統的核心參數之一，可為整車電池組的控制策略提供判斷依據。一般通過對鋰電池輸出電壓、負載電流和工作溫度等參數的實時監測實現SOC估計，進而實現鋰電池充放電控制、熱管理等功能。同時，SOC估計精確與否直接影響著鋰電池輸出特性、使用壽命和安全性能等。

目前常用的SOC 估計方法分為2 種：一是根據鋰電池輸出參數（電流、電壓）直接計算得到，如安時積分法、開路電壓法等；二是基于鋰電池模型并結合預測算法得到，如神經網絡法、粒子濾波算法、卡爾曼濾波算法等。安時積分法需要獲得精確的SOC初值，在初值未知的情況下估計誤差大，不適用于實際車輛；開路電壓法需要將放電后的鋰電池擱置較長時間，不滿足SOC估計的實時性要求；神經網絡法需要大量不同工況下鋰電池試驗數據訓練神經網絡模型，模型精度與模型大小不可兼得，實際應用還存在一定困難；粒子濾波算法計算復雜，對硬件性能要求高；卡爾曼濾波算法是目前比較成熟且有效的一種方法，計算簡單且精度高，適用于SOC 的實時估計。因此本文在卡爾曼濾波算法的基礎上對鋰電池SOC估計進行研究。

傳統的卡爾曼濾波算法不適用于非線性系統，因此許多學者提出了擴展卡爾曼濾波（Extended Kalman Filter，EKF）和無跡卡爾曼濾波（Unscented Kalman Filter，UKF）。EKF 利用泰勒級數展開將非線性系統轉化為線性系統，忽略了高階項導致其用于高度非線性系統時算法精度降低且雅可比矩陣計算復雜；UKF 通過無跡變換獲得Sigma 點集，Sigma 點集通過非線性函數進行傳遞，再利用傳遞結果更新狀態均值與系統協方差。UKF 在估算SOC 時，假定系統噪聲為恒定的高斯白噪聲。但在實際工作過程中，鋰電池系統噪聲特性復雜多變，具有不確定性。

針對UKF估計鋰電池SOC時對不確定系統噪聲估計精度低的問題，本文提出基于自適應無跡卡爾曼濾波（Adaptive Untracked Kalman Filter，AUKF）的估計算法，在SOC 估計的同時不斷更新系統狀態噪聲協方差和測量噪聲協方差，以提高算法的精度和穩定性。

2 建立等效電路模型

2.1 狀態空間方程

等效電路模型是依據鋰電池充放電試驗數據并利用電壓源、電阻、電容等電子元件而建立的模型。等效電路模型包括內阻等效（Rint）模型、戴維南（Thevenin）模型、新一代汽車合作伙伴計劃（Partnership for a New Generation of Vehicles，PNGV）模型、非線性等效（General Nonlinear，GNL）模型等。

綜合考慮模型參數的計算難易程度與模型精度，本文選擇Thevenin模型，并考慮到模型需要充分反映鋰電池充放電特性，在Thevenin 模型基礎上增加1 個RC 網絡以提高模型精度，等效電路模型如圖1所示。

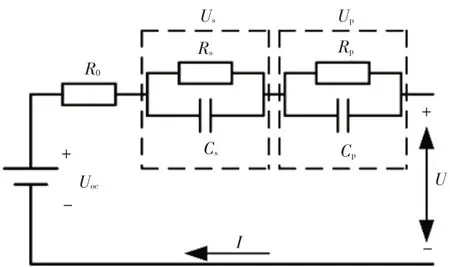
圖1 二階RC等效電路模型

圖1中：為鋰電池開路電壓；為歐姆內阻；、分別為電化學極化內阻和濃差極化內阻；、分別為電化學極化電容和濃差極化電容；、分別為電化學極化電壓和濃差極化電壓；為輸出電壓；為負載電流。電路物理量描述為：

式中，(0)、(0)分別為初始的電化學極化電壓和初始的濃差極化電壓；=、=分別為電化學極化時間常數和濃差極化時間常數。

利用卡爾曼濾波估計SOC時，要將鋰電池系統模型離散化，以SOC 與2 個極化電壓作為系統狀態變量，電流作為輸入變量。根據安時積分法和式（1）得到鋰電池系統模型離散化狀態方程：

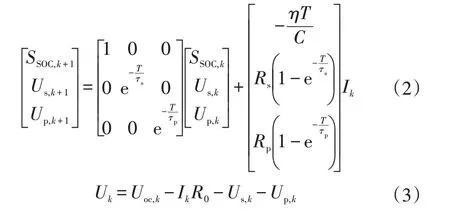
式中，為時刻鋰電池的SOC；為電流采樣周期；為庫倫效率，與鋰電池工作溫度、循環次數和放電倍率有關；為額定容量。

2.2 模型參數辨識

本文鋰電池試驗平臺由Neware BTS8000 電池檢測設備、多功能夾具、恒溫恒濕試驗箱和控制電腦組成。試驗對象為N18650CK三元鋰電池，其部分性能參數如表1所示。

表1 鋰電池性能參數

為獲得鋰電池開路電壓以及等效電路模型中參數與SOC的函數關系，需對鋰電池進行混合脈沖功率特性（Hybrid Pulse Power Characteristic，HPPC）試驗，試驗流程如圖2所示，部分試驗數據如圖3所示。

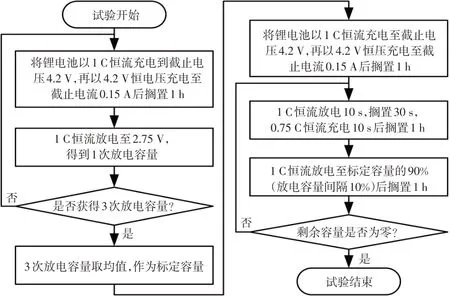
圖2 鋰電池充放電試驗流程

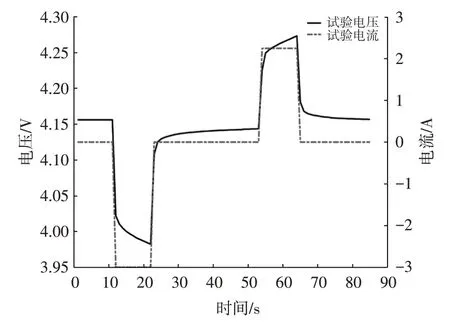
圖3 鋰電池部分充放電試驗數據

根據上述試驗，獲得不同SOC狀態下對應的開路電壓，利用MATLAB 對試驗數據進行多項式擬合，結果如圖4所示，所得到的六階多項式擬合函數為：

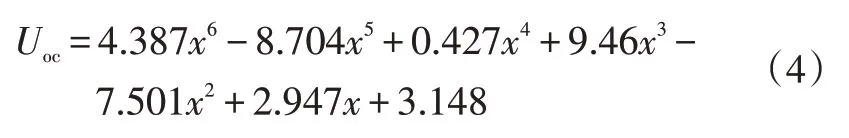
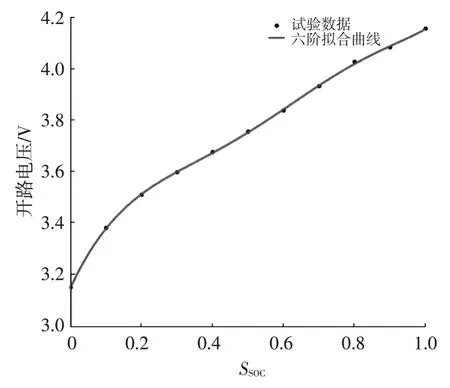
圖4 開路電壓與SOC的函數擬合曲線

系統參數辨識中，遞推最小二乘法因編程簡單、收斂速度快、計算量小等優點被廣泛使用。與最小二乘法相比，遞推最小二乘法利用當前時刻試驗數據和上一時刻辨識參數直接對當前時刻辨識參數進行修正，用于在線參數辨識時可減小計算量，更適用于鋰電池SOC 的在線實時估計，但是遞推最小二乘法存在“數據飽和”問題，即舊數據的堆積導致遞推結果不能反映新數據的特性。故本文采用帶遺忘因子的遞推最小二乘（Forgetting Factor Recursive Least Square，FFRLS）算法辨識鋰電池模型中的參數。加入遺忘因子可以加強新數據的特性，逐漸削弱舊數據的作用，在一定程度上解決了數據飽和問題。FFRLS算法公式為：

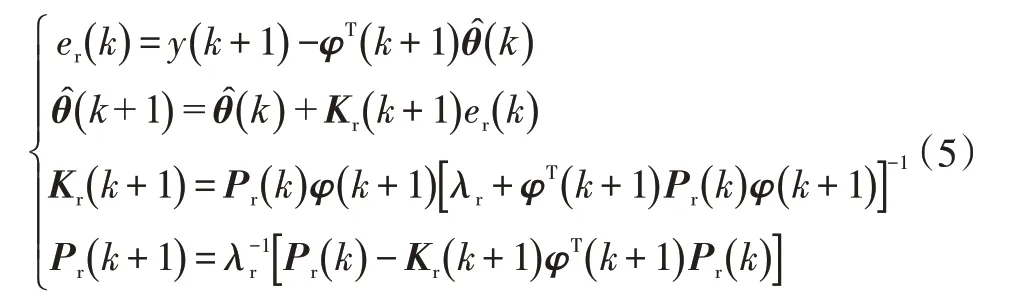
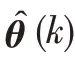
鋰電池等效電路模型拉普拉斯方程與傳遞函數為：

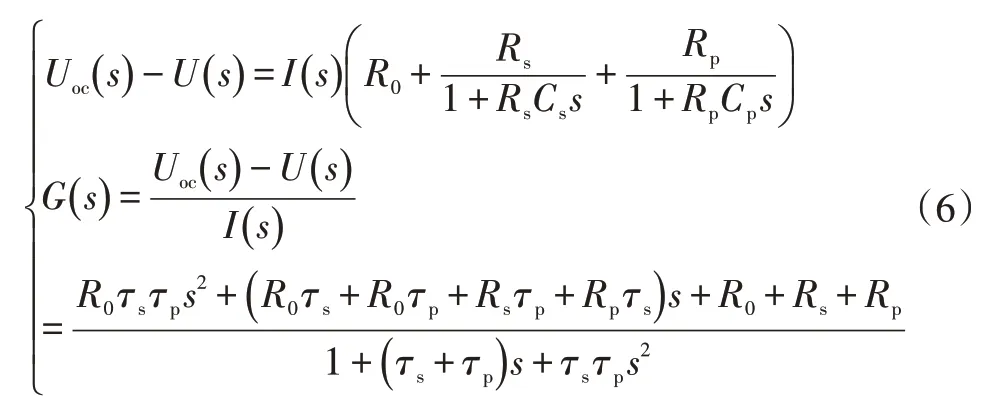
式中，()為系統傳遞函數；為拉普拉斯算子。

雙線性變換公式為：

式中，為域變量。

利用式（7）對式（6）進行離散化并轉化為差分方程：

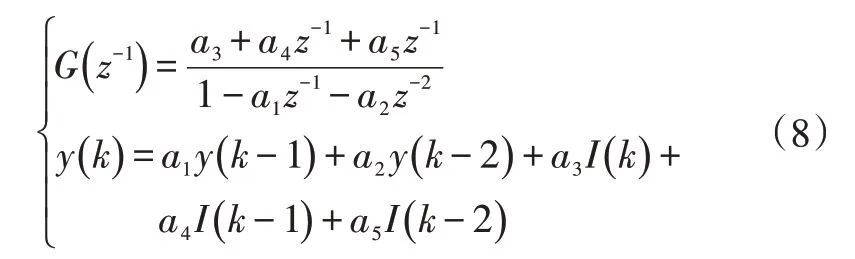
式中，～為待定系數。

將()轉化為矩陣形式：

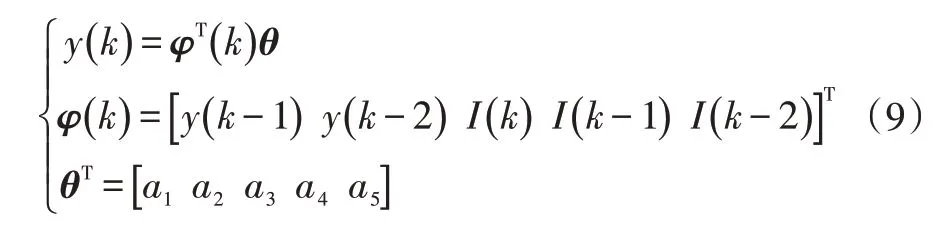
根據式（6）、式（8）可得到鋰電池模型參數計算公式：

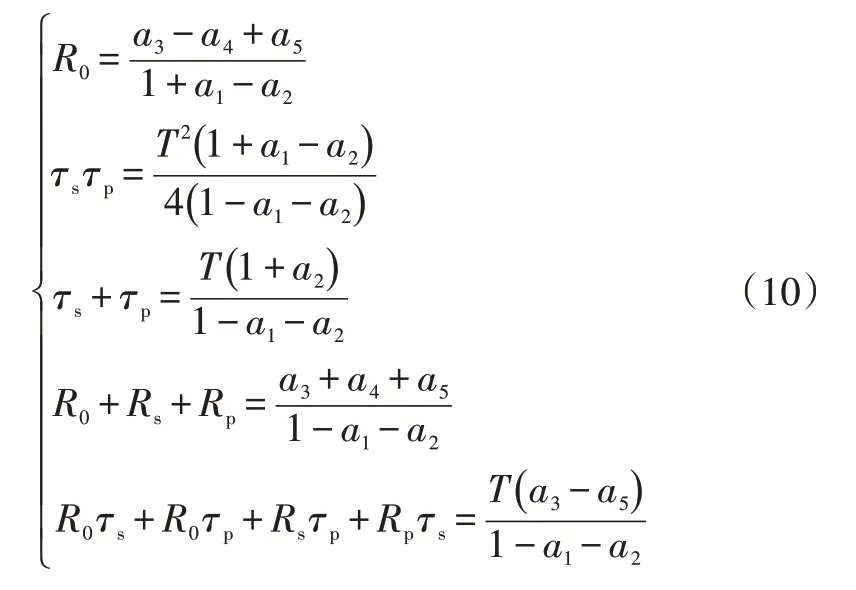
利用上述公式和HPPC試驗數據，可辨識出等效電路模型參數。如圖5所示為荷電狀態=1時辨識參數變化過程。

分析圖5 可知，FFRLS 在辨識開始階段，模型參數變化較大，這是因為所設置的參數初值誤差大，隨著算法迭代次數增加，模型各參數逐漸趨于穩定。其中<，<，表明電化學極化時間常數小于濃差極化時間常數，滿足鋰電池在放電過程中電化學極化響應快于濃差極化響應的特性。

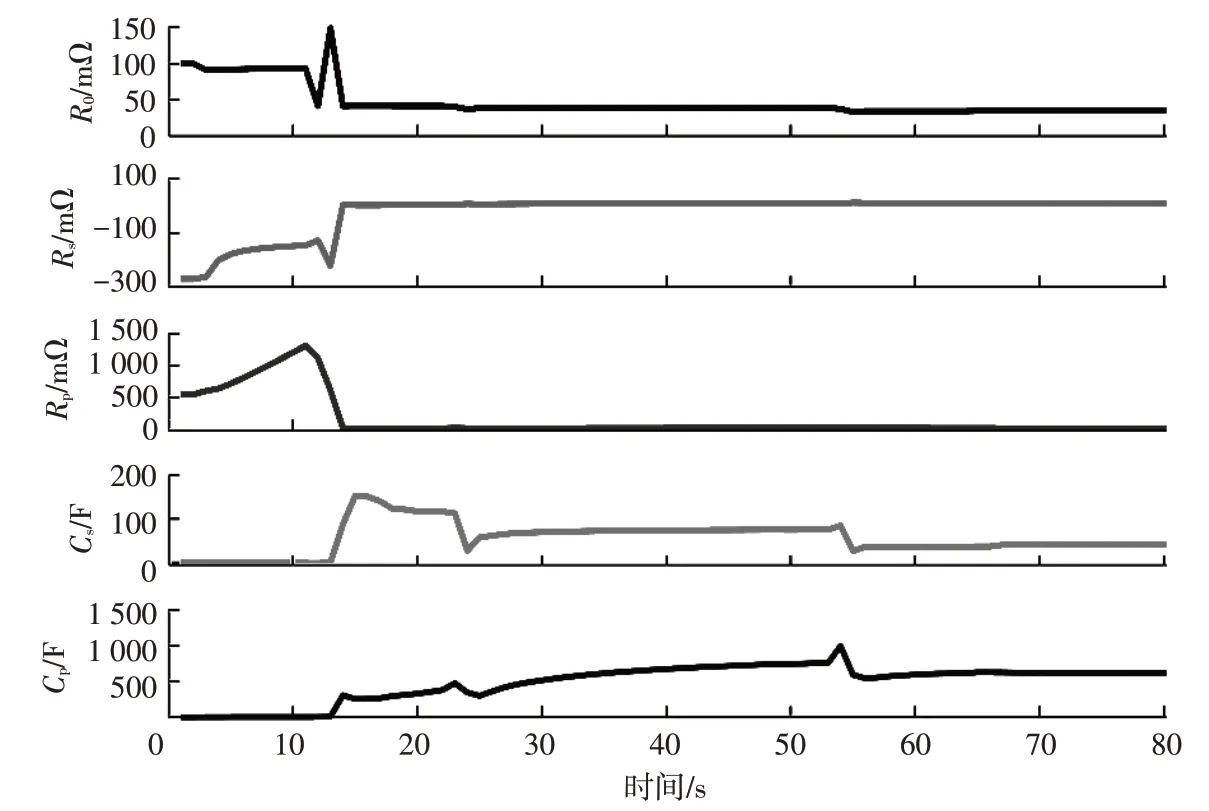
圖5 SSOC=1時參數變化曲線

不同SOC 辨識結果如表2 所示，根據參數辨識結果，利用MATLAB 可擬合出各參數與SOC 的函數關系。

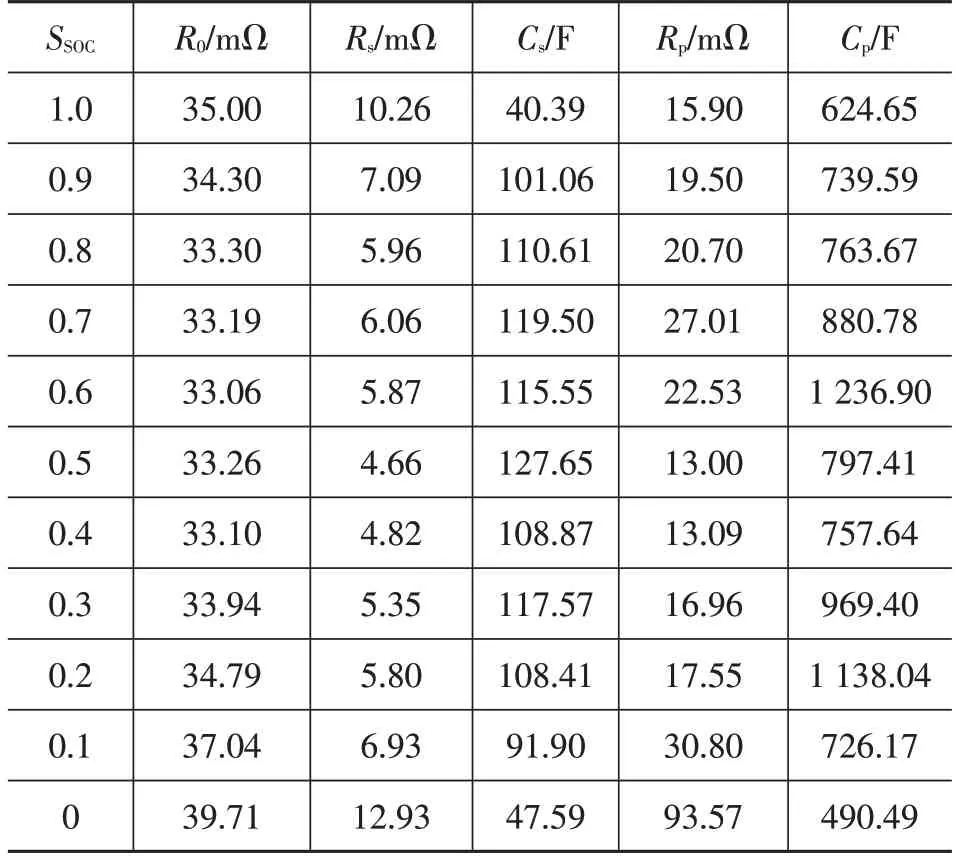
表2 等效電路模型參數表

2.3 模型驗證

本文利用脈沖放電試驗驗證二階RC等效電路模型與參數辨識的精確度。試驗電流與電壓曲線如圖6 所示，模型輸出電壓與試驗電壓的誤差如圖7所示。

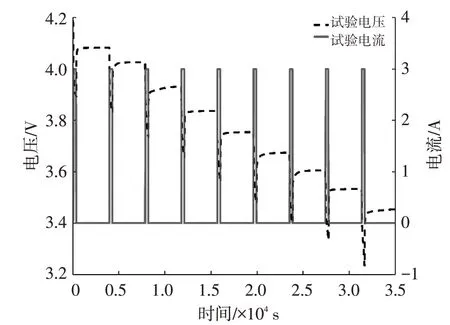
圖6 脈沖放電曲線

分析圖7可知，模型輸出電壓與試驗電壓變化趨勢一致，隨著放電的進行，模型輸出電壓誤差逐漸增大，這是放電末期等效電路模型不能很好地表征鋰電池內部實際的電化學反應導致的。計算誤差結果可知，模型輸出電壓與試驗電壓相比，平均誤差為0.89%，最大誤差在3%以內，所建立的模型具有較高精度，能反映鋰電池輸出特性。

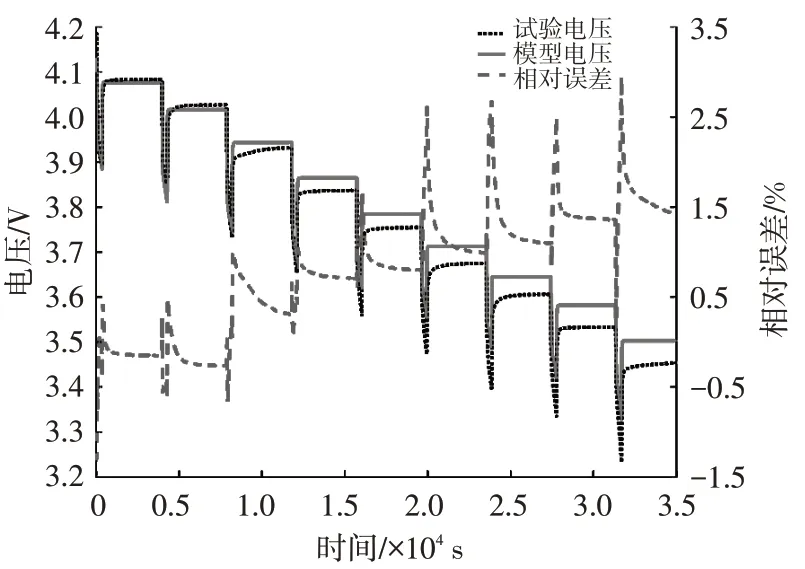
圖7 試驗電壓與模型電壓誤差曲線

3 鋰電池SOC估算

鋰電池為高度非線性系統，輸出特性不僅與自身狀態（放電倍率、老化程度等）有關，還與外界環境（溫度、濕度等）有關。EFK的泰勒級數展開過程中忽略了高階項的影響，降低了SOC估計精度。UKF通過無跡變換對非線性函數的概率分布進行近似處理，保證了對高度非線性系統的預測精度。鋰電池系統真實狀態方程與觀測方程為：

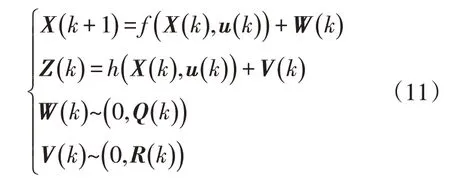
式中，()為式（2）所述系統狀態變量；()為觀測變量（輸出電壓）；()為輸入變量（電流）；為鋰電池狀態方程函數；為觀測方程函數；()、()分別為狀態噪聲和觀測噪聲，均值均為零；()、()分別為()、()的協方差。

由于UKF 忽略了系統噪聲特性的變化，影響了估計精度，因此將UKF 與Sage-Husa 自適應算法結合成AUKF，從而考慮系統噪聲協方差的變化。AUKF 估算鋰電池SOC流程如下：

a.初始化狀態變量均值與協方差：

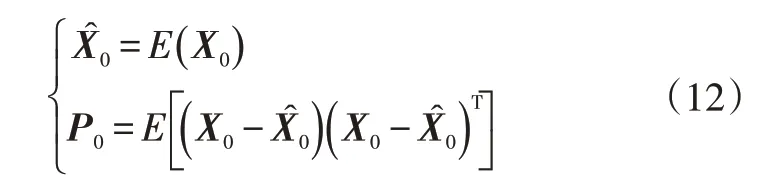
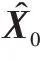
b.產生Sigma點：

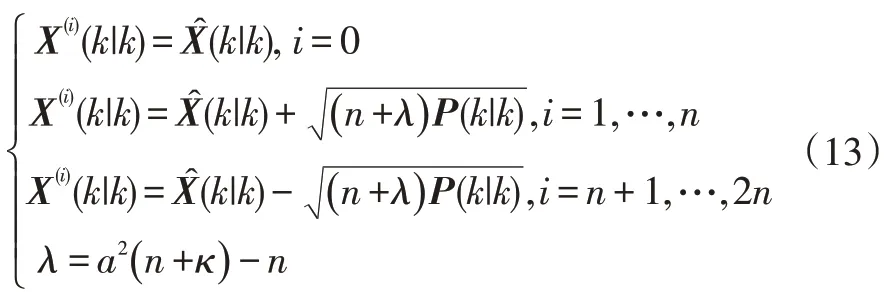
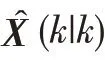
c.計算Sigma點的權值：

d.預測Sigma點：

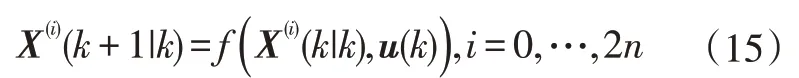
式中，X(+1|)為(2+1)個預測Sigma點。

e.預測系統狀態變量及協方差：

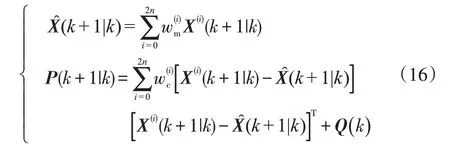
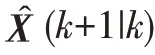
f.再次進行無跡變換，產生新的Sigma點：

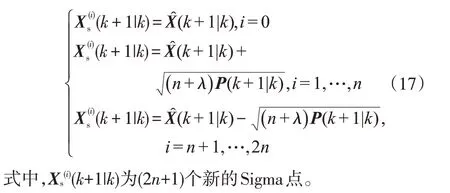
g.預測觀測變量及其均值：

h.計算卡爾曼增益：

i.更新狀態變量與變量協方差：

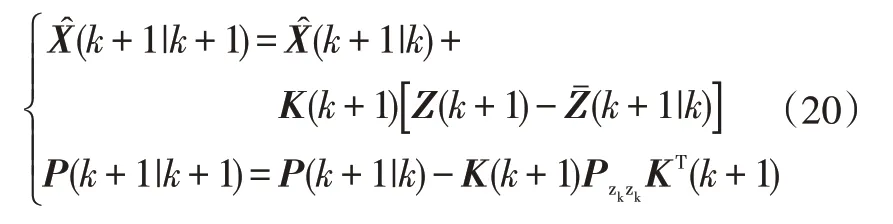
j.更新狀態噪聲協方差與觀測噪聲：

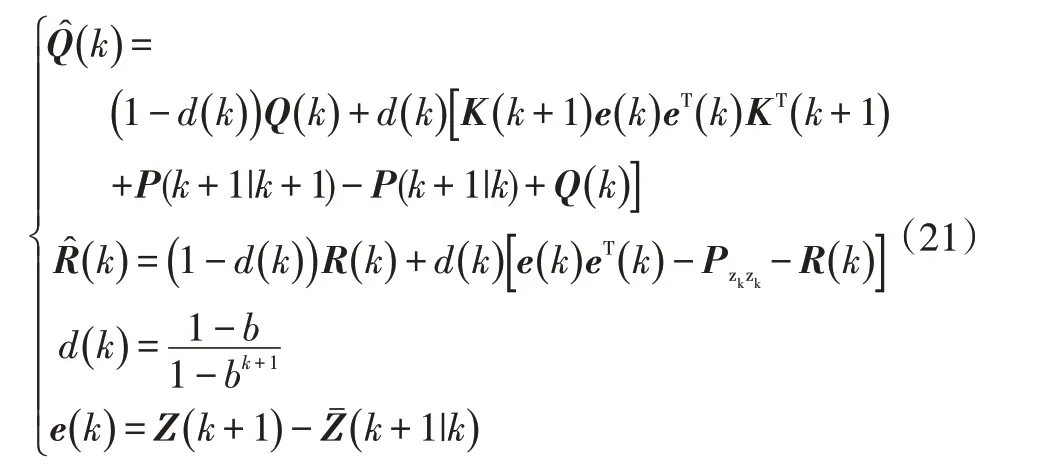
式中，()為自適應因子；()為殘差；為遺忘因子，通常0.95≤≤1，本文取=0.97。

式（21）可以保證AUKF估計SOC時，實時更新鋰電池系統狀態噪聲與觀測噪聲特性，進而提高算法估計精度和穩定性。但如果狀態變量協方差為非對稱正定矩陣，則無法進行楚列斯基（Cholesky）分解，導致算法無法估計，考慮到狀態噪聲協方差和觀測噪聲協方差會影響系統狀態協方差且兩者都為互不相關的高斯白噪聲，協方差矩陣均為對角矩陣，因此對狀態噪聲協方差與觀測噪聲協方差進行修正：

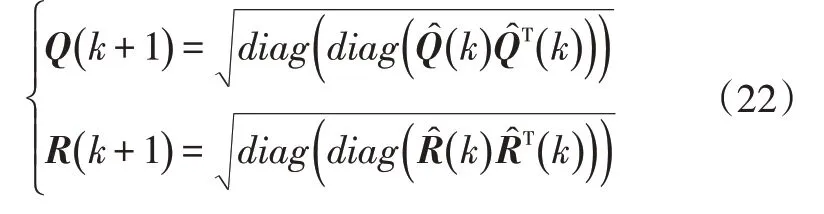
4 結果驗證與分析

將FFRLS 辨識所得參數分別結合UKF 和AUKF 估計鋰電池SOC，其主要步驟如圖8所示。鋰電池在實際使用過程中，工作情況復雜，因此使用美國城市循環（Urban Dynamometer Driving Schedule，UDDS）工況對算法進行驗證。本文所用鋰電池最大放電電流為9 A，最大充電電流為3 A，將工況電流縮放到鋰電池安全適用范圍內。考慮到過度放電會損傷鋰電池甚至使其直接報廢，因此將UDDS 工況循環13 次后停止放電，假設放電電流方向為正，仿真電流如圖9所示。

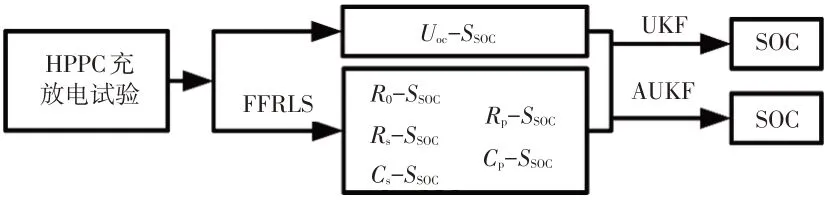
圖8 鋰電池SOC估計流程

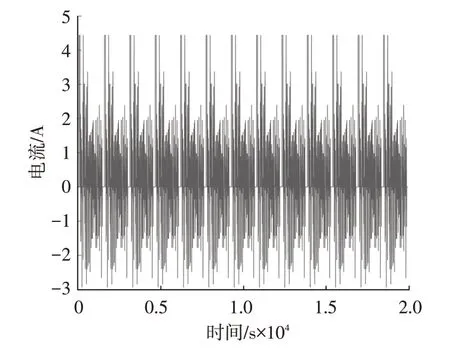
圖9 仿真電流數據

實際情況下SOC 初值未知，本文將算法的SOC 初值設置為0.8，將安時積分法計算所得SOC 設為參考值。UKF和AUKF的SOC估計結果如圖10所示，SOC估計誤差如圖11 所示。分析圖10、圖11 可知，UKF 和AUKF對鋰電池UDDS放電工況下的SOC估計都有著很好的跟蹤效果，在初值不準確的情況下，均能快速收斂于參考值并且AUKF 的波動情況明顯小于UKF。這是因為UKF忽略了系統噪聲特性的變化，而AUKF能實時更新系統噪聲特性并利用噪聲協方差的估計結果修正SOC估計值，從而減小了估計誤差。

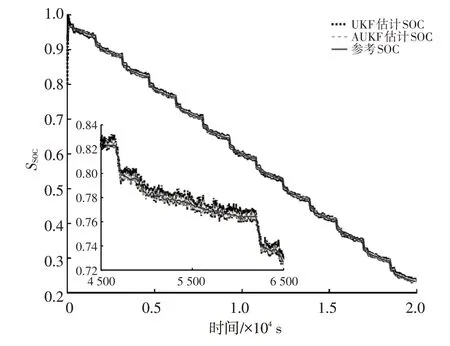
圖10 參考曲線與算法估計曲線

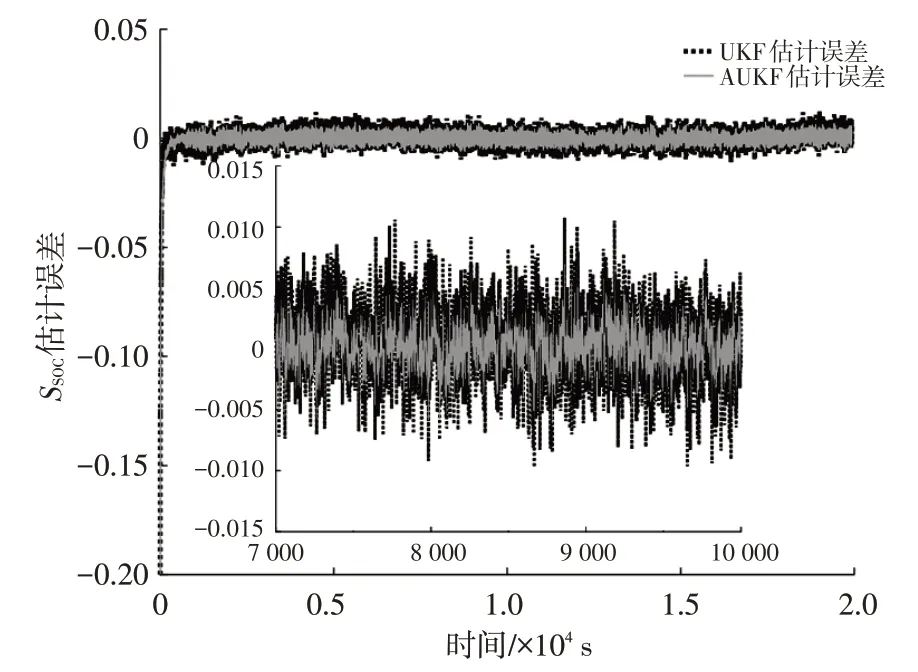
圖11 算法估計誤差曲線

本文利用最大相對誤差和均方根誤差對比UKF和AUKF 的算法性能，最大相對誤差和均方根誤差越小，代表算法對SOC估計效果越好。不考慮前800 s算法收斂過程，兩者的誤差計算結果如表3所示。

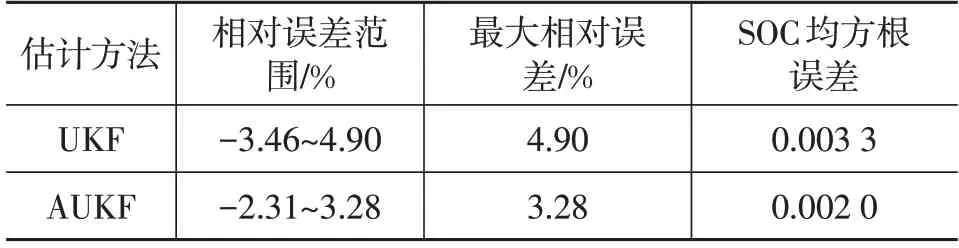
表3 UKF和AUKF誤差計算結果

分析表3 可知，AUKF 的最大相對誤差與均方根誤差均小于UKF。相比于UKF，AUKF最大相對誤差減小了1.62 百分點，均方根誤差減小了0.001 3，AUKF 算法對鋰電池SOC估計結果更好。

5 結束語

本文基于鋰電池二階RC 等效電路模型，采用FFRLS參數辨識的方法得到鋰電池模型中的各參數，利用MATLAB將UKF與AUKF進行對比仿真。結果表明，鋰電池在噪聲復雜工況下工作時，相比于UKF，AUKF的最大相對誤差減小了1.62百分點，均方根誤差減小了0.001 3。AUKF能實時調整系統噪聲統計特性，因此具有更高的精度和更好的穩定性。