例談超幾何分布與二項分布的辨析

王 進

(山東省淄博市高青縣第一中學)

超幾何分布、二項分布是高考常考的概率分布類型，這兩種分布既有區別，又有關聯，學生在初學時由于對兩種分布的本質認識不清，極易造成混淆，進而在解題中出現錯解.那么如何區分這兩種分布?筆者歸納出如下幾個區分點，供讀者參考.

1 在每次試驗中某一事件發生的概率相同還是不同

辨析從概念上來看:若隨機變量X的分布列為(k＝0，1，2，…，l，l＝min{n，M})，則稱X服從超幾何分布.若隨機變量X的分布列為1，p＋q＝1)，則稱X服從二項分布.從中可以看出，二項分布在每次試驗中某一事件發生的概率是不變的，超幾何分布是變化的.

例1某大型國際活動招募了50萬青年志愿者，根據性別分層抽樣，從中隨機選取20人進行英語水平測試，所得成績(單位:分)如圖1所示.

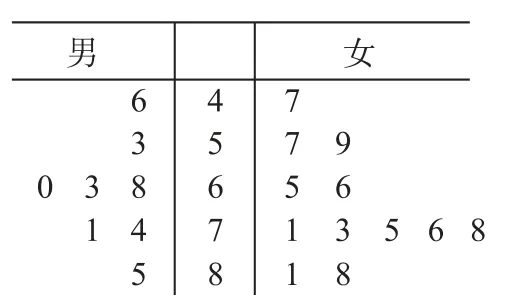
圖1

(1)從選出的8名男生中隨機連續選取2次，每次選1人，記其中測試成績在70分以上的人數為X，求X的分布列和數學期望;

(2)為便于聯絡，現將所有青年志愿者隨機分成若干組(每組人數不少于5000)，并在每組中隨機選取m人作為聯絡員，要求每組聯絡員至少有1人英語成績在70分以上的概率大于90%.根據圖中數據，以頻率作為概率，求m的最小值.

分析本題第(1)問從8人中隨機連續選取2次，每次選取1人，第一次選取的學生成績在70分以上的概率，與第二次選取的學生成績在70以上的概率不同，故X服從超幾何分布.第(2)問中每個志愿者的英語成績在70分以上的概率都是相互之間互不影響，概率不變，故X服從二項分布.

解(1)8名男生中70分以上的有3人，故X的可能取值為0，1，2.

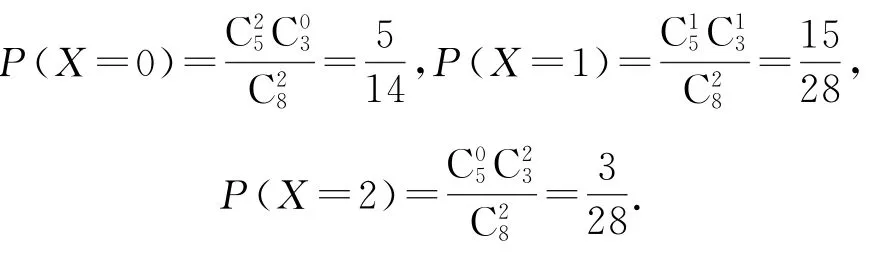
因此，X的分布列如表1所示.

表1

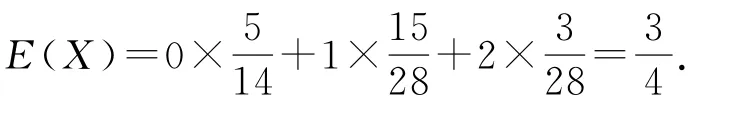
(2)由圖1中的數據可知20人中英語成績在70分以上的有10人，故從中任取1人，其成績在70分以上的概率為人中至少有1人成績在70分以上，情況較多，包括1人，2人，…，m人.據對立事件的原理得，即m的最小值為4.

2 抽取方式是有放回還是無放回

辨析教材中對兩種分布的模型解釋:在N件產品中有M件次品，無放回地任取n件，其中次品數X服從超幾何分布.在N件產品中有M件次品，有放回地任取n件，其中次品數X服從二項分布.從中可以看出抽取方式是有放回還是無放回，這是判斷超幾何分布與二項分布的一個關鍵條件.超幾何分布是無放回，二項分布是有放回.

例2某套高考模擬試卷中單選題共有8道，已知小明能答對其中的6道.

(1)小明從中任選4道題作答，設答對題目的個數為X，求X的數學期望;

(2)小明從中每次取出1道題作答，取出后放回，連取4次，設答對題目的個數為Y，求Y的數學期望.

分析第(1)問從8道題中選4道，可理解為“一把抓”，沒有順序.第(2)問每次取1道題，有順序，且取出后再放回，即第一次取時，8道題中有6道題會答，第二次再取時，仍是8道題中有6道題會答，每次取題互不影響，即獨立重復，共重復了4次，故服從二項分布.

解(1)8道題中能答對6道，從中任選4道題，則至少能答對2道，故X的可能取值為2，3，4，相應的概率分別為

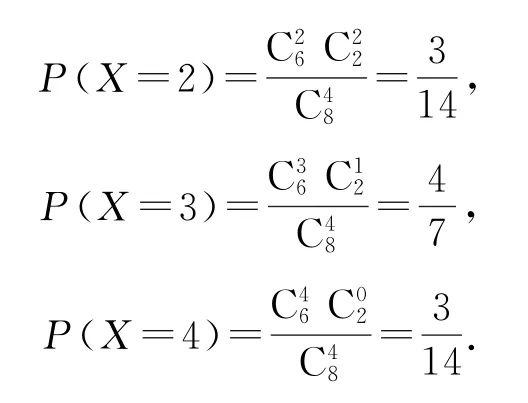
因此，X的分布列如表2所示.

表2

(2)每次取出1道題，取出后放回，8道題中有6道能答對，故每次取題答對的概率為連續取4次，即進行4次獨立重復試驗，答對題目的個數Y的可能取值為0，1，2，3，4.

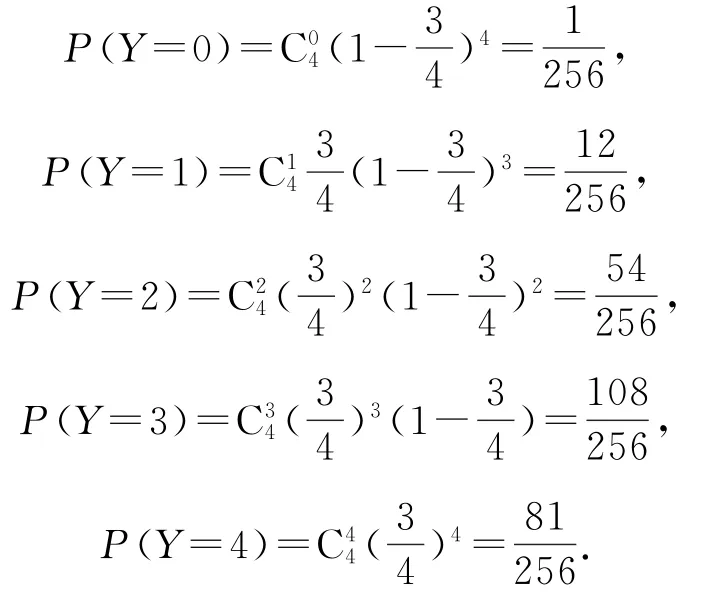
因此，Y的分布列如表3所示.

表3

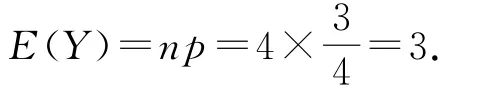
3 抽取范圍是總體還是樣本

辨析在概率統計的應用中，我們常用樣本數據特征來估計總體.因此在試驗活動中，要明確是在總體中抽取，還是在樣本中抽取.若在總體中抽取，甚至在某些情況下總體數量是不確定的，此時應按二項分布的類型來處理.若在樣本中抽取，且無放回，則按超幾何分布來處理.

例3每年的4月23日是聯合國教科文組織確定的“世界讀書日”，又稱“世界圖書和版權日”，為了解某地區高一學生閱讀時間的分配情況，從該地區隨機抽取了500名高一學生進行在線調查，得到了這500名學生的日平均閱讀時間(單位:h)，并將樣本數據分成[0，2]，(2，4]，(4，6]，(6，8]，(8，10]，(10，12]，(12，14]，(14，16]，(16，18]這9組，繪制成如圖2所示的頻率分布直方圖.

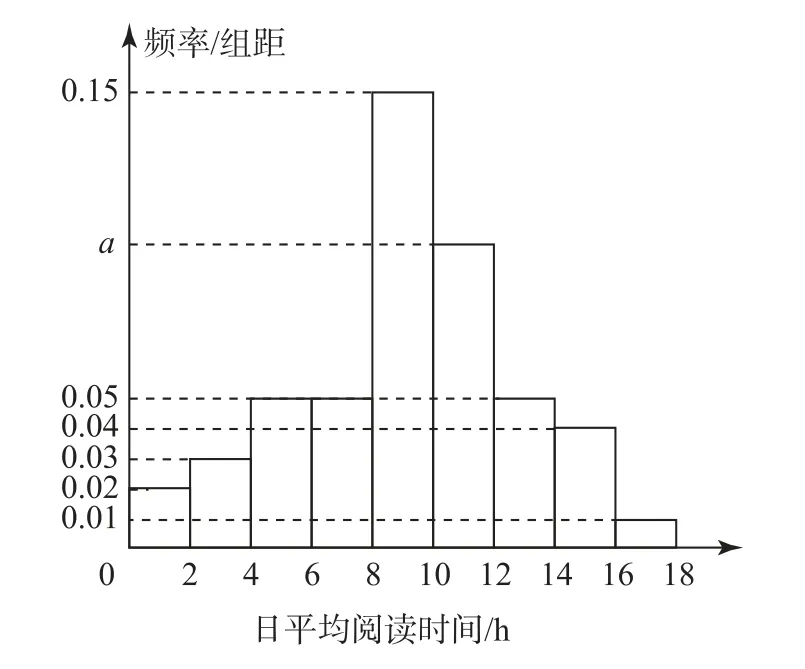
圖2

(1)求a的值;

(2)為進一步了解這500名學生數字媒體閱讀時間和紙質圖書閱讀時間的分配情況，從日平均閱讀時間在(12，14]，(14，16]，(16，18]這3組內的學生中，采用分層抽樣的方法抽取了10人.現從這10人中隨機抽取3人，記日平均閱讀時間在(14，16]內的學生人數為X，求X的分布列;

(3)以調查結果的頻率估計概率，從該地區所有高一學生中隨機抽取3名學生，記日平均閱讀時間在(10，12]內的學生人數為X，求X的分布列及數學期望.

分析本題第(2)問，是從分層抽樣得到的10人中，無放回任選3人，隨機變量X服從超幾何分布.第(3)問，是從地區所有高一學生中抽取，且總體人數不確定，故X服從二項分布.

解(1)a＝0.1(求解過程略).

(2)根據分層抽樣原理，可知在閱讀時間為(12，14]，(14，16]，(16，18]內抽到的學生人數分別為5人，4人，1人.

從這10人中任選3人，則閱讀時間在(14，16]內的人數X的可能取值為0，1，2，3，則

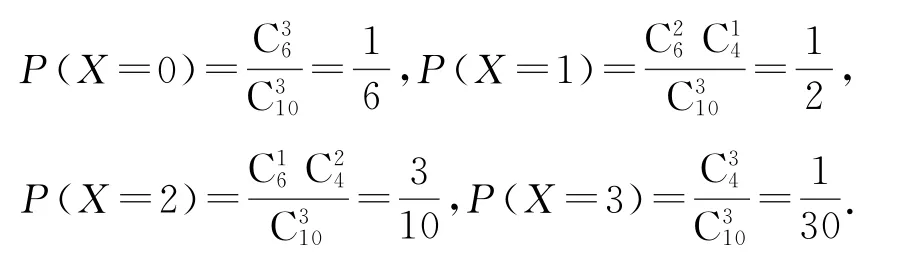
因此，X的分布列如表4所示.

表4

(3)由題意及(1)的結論知，從該地區所有高一學生中隨機抽取1名學生，平均閱讀時間在(10，12]內的概率為因該地區高一學生總人數不確定，故每次抽取概率不變，抽取3次，即進行3次獨立重復試驗.

X的可能取值為0，1，2，3，相應的概率分別為

因此，X的概率分布列如表5所示.

表5

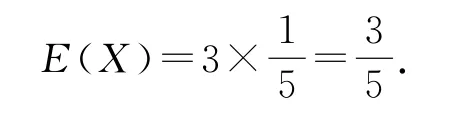
4 總體數量是多還是少

辨析超幾何分布與二項分布既有區別，又有聯系.當總體的數量非常大，抽取樣本數量很少時，可以近似地認為每次抽取時事件發生的概率不變，這樣就可以看成每次抽取結果是相互獨立的，進而將超幾何分布近似地看作二項分布來處理.

例4某手機生產商一批次生產了50000臺手機，其中次品率是2%，現從中不放回地依次抽取3臺進行檢驗.求抽到次品臺數X的概率分布列.

分析本題抽取方式為無放回，因此從問題的本質來看，屬于超幾何分布.手機總臺數為50000，其中次品為臺，合格的手機為49000臺.現從50000臺中抽取3臺，則X的可能取值為0，1，2，3.我們先按古典概率類型來計算X取某一值時的概率，比如X＝1.

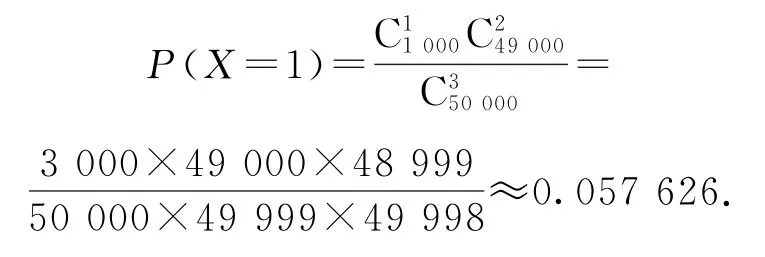
因為總體數非常大，第一次抽取與第二次、第三次抽取次品率非常接近，我們可以認為每次抽到次品率均為2%，抽取3次，即3次獨立重復試驗，故抽到的次品數近似服從二項分布，此時

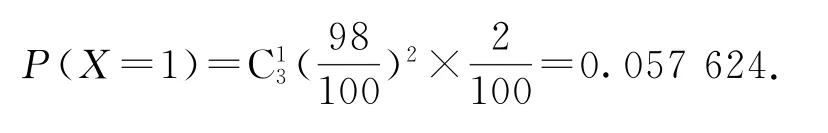
不難發現這兩種計算方式所得的概率幾乎相等，因此這種情況，我們可按獨立重復概率類型來處理.

解X的可能取值為0，1，2，3.

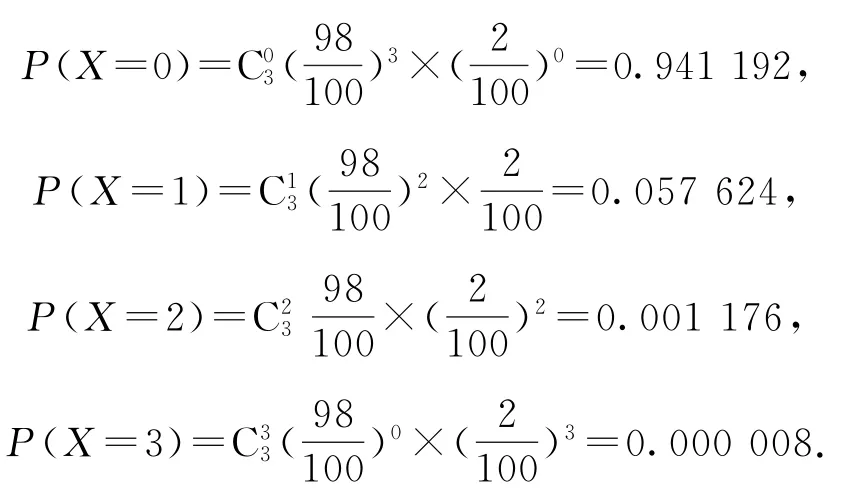
因此，X的概率分布列如表6所示.

表6

另外，常見的概率分布類型還有兩點分布，兩點分布是一種特殊的二項分布，即只進行一次獨立重復試驗，只有發生與不發生兩種結果，與其有關的問題相對于前兩種要簡單一些.

總之，在處理與概率分布有關的問題時，我們要明確各種概率分布的本質，以及不同概率類型之間的異同，結合題目條件，準確識別概率類型.