覆蓋型巖溶塌陷動態演化數值模型研究
熊啟華,高 旭,徐 慶,王芮瓊,李祖春,陶 良
(1.湖北省地質環境總站,湖北 武漢 430039;2.中國地質大學(武漢)工程學院,湖北 武漢 430074;3.武漢市測繪研究院,湖北 武漢 430022)
覆蓋型巖溶塌陷具有表觀突發性和內部漸進性的特點,塌陷的發生是在覆蓋層內土洞逐漸演化擴展至極限尺寸后,頂板強度不足以支撐其自重而突然失穩垮塌。因此,預測不同水動力環境下巖溶覆蓋層土洞的發育規模和極限規模尺寸對于評價覆蓋層穩定性意義重大。然而受制于土洞發育的隱蔽性和物探解譯的多解性,直接通過技術手段查明土洞發育尺寸的難度較大或精度不高。鑒于此,從土洞發育物理力學機理出發來建立一種定量預測土洞發育規模和穩定性評價的數值模型(即覆蓋型巖溶塌陷動態演化數值模型)并加以驗證是本文的研究目標。
目前,以地下水變動為主要誘發因素的巖溶覆蓋層中土洞發育的機理主要有潛蝕論和真空吸蝕論兩種[1]。潛蝕論認為在巖溶溶隙開口附近的水力梯度超過覆蓋層土體臨界水力梯度而發生潛蝕或剝蝕,形成土洞并逐漸擴展;真空吸蝕論認為地下水水位在覆蓋層與溶腔開口交界處上下波動或快速抽吸巖溶水形成負壓而使土層剝蝕擴洞。
而目前針對覆蓋型巖溶塌陷機理的研究方法主要有解析法、物理模型試驗法和數值模擬法。其中,解析法多是基于普氏平衡拱理論探索臨界土洞的規模大小[2]或采用極限平衡理論分析給定幾何尺寸下土洞頂板的穩定性狀態[3]。雖然利用物理模型試驗方法來研究覆蓋型巖溶塌陷機理的學者較多[4-5],但定量研究土洞動態發育特征的物理模型試驗較少,僅見有:吳慶華等[6]采用恒壓取樣技術獲取巖溶塌陷物理模型試驗過程中砂土漏失質量,用來定量評估土洞的發育過程;張少波等[7]通過在物理模型土層中間隔一定距離布設孔隙水壓力自動監測點,通過監測土洞發育過程中造成的不同位置處孔隙水壓力變化的差異來判定土洞的發育階段。然而,目前物理模型試驗很難判定不同發育階段土洞所對應的穩定性狀態。鑒于此,部分學者利用數值模擬手段來評估土洞的穩定性,如:孫金輝[8]結合物理模型試驗并基于FLAC3D建立了不同規模尺寸土洞開挖數值模型,探索覆蓋層地表沉降和內部應力-應變過程;陳冬琴等[9]建立了巖溶塌陷地下水-力學耦合數值模型,并基于此對土-巖交界處溶洞塌陷進行了地下水水位升降及降雨入滲作用對巖溶塌陷的影響分析。
上述研究基本都是人為設定土洞尺寸再進行數值模擬,并不是自適應的土洞擴展演化過程。鑒于此,本文以潛蝕論為基本出發點,建立了覆蓋型巖溶塌陷動態演化數值模型,并用于土洞發育規模預測。首先,以武漢市烽火村巖溶塌陷實例為分析對象,概化其巖溶塌陷工程地質模型,并建立滲流-力學單向耦合控制方程,同時結合土洞剝蝕判據編制覆蓋型巖溶塌陷動態演化計算程序;然后,基于此程序預測在不同水動力環境條件下覆蓋層中潛在土洞的發育規模,并提出臨界致塌水位差和極限土洞尺寸;最后,基于普氏平衡拱理論對預測結果進行驗證分析。
1 覆蓋型巖溶塌陷動態演化數值模型
1.1 覆蓋型巖溶塌陷工程地質模型概化
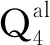

圖1 烽火村覆蓋型巖溶塌陷地質剖面圖
據此,將烽火村覆蓋型巖溶塌陷概化為如圖2所示的工程地質模型,其覆蓋層總厚度為30 m,黏砂層厚度比為1∶5,模型尺寸為100 m×35 m,其中基巖厚度為5 m,網格剖分為1 m×1 m單元。
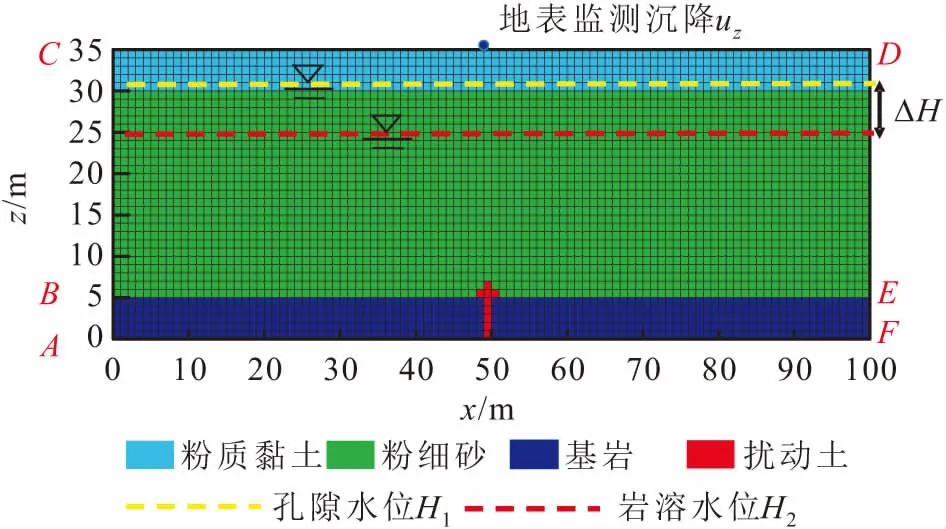
圖2 烽火村覆蓋型巖溶塌陷工程地質概化模型
該巖溶塌陷是長期人工抽取地下水誘發的,定性分析認為覆蓋層中孔隙水位常常高于巖溶水位,導致存在孔隙水向巖溶水補給滲流過程中當水力梯度超過某一臨界值時出現砂土潛蝕或剝蝕現象。土洞剝蝕類似地下工程開挖卸荷,必然伴隨著洞周應力重分布、地表沉降、塑性區發展等一系列力學響應;加之,地下水滲流場的存在不僅是土洞剝蝕的直接動力源,同時也造成對土洞的滲流荷載。因此,在滲流荷載與卸荷荷載聯合作用下,當土洞的應力、應變超過其極限狀態時則產生巖溶塌陷。
鑒于此,覆蓋型巖溶塌陷動態演化數值模型就是建立起能夠描述地下水流場中土洞擴展的滲流-力學單向耦合控制方程(此處單向耦合是指巖土體的應力-應變不改變其滲透性質,而只有滲透力的單方面力學作用),且通過土洞剝蝕判據和土洞應力-應變狀態來控制土洞擴展演化進程。下面闡述滲流-力學單向耦合控制方程式及其所用參數和邊界條件,以及土洞動態演化的計算流程。
1.2 滲流-力學單向耦合控制方程式及其邊界條件
數值模型不考慮剝離后土體的運動狀態,且假定剝離前土洞巖土體介質處于小變形狀態,故采用二維等效連續介質有限元數值模型模擬基巖和覆蓋層地下水流場,以及在地下水滲流作用下土洞剝蝕過程中變形和塑性區的發展過程,故模型的力平衡方程如下:
(1)


(2)
式中:γg為巖土層重度(kN/m3);VA為被剝蝕單元體積(m3);[B]為關于應變與位移之間關系的幾何矩陣;[N]為典型四節點等參單元形函數。
另一方面,作用于非剝蝕單元節點上的滲透力則是與地下水滲流梯度有關[10],其滲流荷載的數學表達式為
(3)
式中:γw為地下水的單位重度(kN/m3),取10 kN/m3;Ω為土洞外滲流區域;H表示總水頭(m),其與壓力水頭p(m)的關系式為H=Z+p,其中Z表示節點豎向高度(m)。
一方面,考慮到研究區覆蓋層內土洞埋深一般在30 m以淺,所處圍壓環境較小,巖土體材料一般不會出現應變硬化特性,但由于采用巖土體應變軟化彈塑性本構模型來描述其達到峰值強度后應力-應變關系的參數難以測定,故綜合考慮采用巖土體屈服極限不隨應力狀態改變而改變的理想彈塑性模型來描述土洞的非線性應力-應變過程;另一方面,考慮到巖土體材料屬于摩擦型材料,故采用最常用的Mohr-Coulomb屈服準則。本模型不考慮巖土體塑性變形過程中的剪脹效應,因此采用非關聯流動法則來描述單元進入塑性狀態后的應變規律,其塑性勢函數中的剪脹角參數設為0。
為了展示土洞演化中存在的塑性區分布情況,定義塑性應變不變量為[11]
(4)
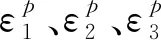
考慮到孔隙水位以上土層處于非飽和狀態,采用變飽和地下水穩定流控制方程來統一描述整個模型中的滲流場:
(5)
式中:p為壓力水頭(m);K(p)為巖土層滲透系數(m/d),對處于飽和狀態(p≥0)的巖土層滲透系數取飽和滲透系數,而對處于孔隙水位以上的非飽和巖土層滲透系數則是壓力水頭的函數,采用最簡單的指數型模型表征為
(6)
式中:Ks為巖土層飽和滲透系數(m/d);αm為孔隙尺寸分布參數(m-1)。
如圖2所示,模型力學邊界條件設置為左右邊界約束水平位移;而底邊界同時約束水平和垂直位移;上邊界為自由邊界。對于水力邊界條件,BC段和DE段設置為總水頭H1的定水頭邊界,代表弱承壓的孔隙含水層水位;而AB段、AF段、EF段則設置為代表巖溶水位H2的可變定水頭邊界,即通過同時調整此三段水頭來模擬不同的巖溶水動力環境條件;上邊界CD段為零流量邊界。
據文獻[14]可知,能使類似地層土洞出現剝蝕的臨界水力梯度(Ibs)取0.5。通過歸納總結相關文獻[15]和《武漢市巖溶塌陷調查子項目成果報告》(編號為1212011220189)確定數值模型所用的滲流和力學計算參數,見表1。

表1 數值模型所用的計算參數
上述公式(5)和(6)所代表的滲流場計算則采用變飽和滲流計算程序vsaft2[16],得出的水頭場根據公式(3)計算出作用在節點上的滲透荷載;然后修改文獻[17]中第6.4.5節關于組裝節點荷載的子程序LOADPS,將滲透荷載和根據公式(2)計算的土洞剝蝕后卸荷荷載組裝成總體荷載矢量;最后由文獻[17]提供的非線性彈塑性力學計算程序完成計算。
1.3 土洞演化的計算流程
結合巖溶塌陷工程地質概化模型和滲流-應力單向耦合控制方程,可得到土洞動態演化計算流程(見圖3)如下:

圖3 土洞動態演化的計算流程
(1) 首先,在溶隙開口部位設置一個幾何較小的初始土洞,土洞和溶隙內都填充擾動土,而其他各巖土層都按原生地層幾何參數賦值。
(2) 在給定的水力邊界條件下按照公式(5)求解滲流場,進而得到水力梯度空間分布。一方面,利用該水力梯度空間分布情況來搜索出與土洞緊鄰的土層單元中水力梯度I大于或等于臨界水力梯度Ibs(即I≥Ibs)的單元,并納入到下一次滲流場計算中的擾動土單元,同時作為下一次應力場計算的剝蝕單元;另一方面,基于水力梯度空間分布,即可根據公式(3)計算出作用在模型中每個單元的滲透力,并結合土洞單元剝蝕卸荷作用,計算模型的力學響應(包括變形和塑性區等)。
(3) 根據新形成的土洞再次進行滲流場和應力場的計算,并重復上述步驟,直到滿足如下兩個終止條件之一:①緊鄰土洞的土層單元水力梯度I全都小于臨界水力梯度Ibs(即I 本文設置模型孔隙水位H1=32 m用于模擬覆蓋層的承壓水環境且保持不變,而通過降低巖溶水位H2用于模擬孔隙水位與巖溶水位之差ΔH(見圖2)穩定在4 m、6 m、8 m、10 m、12 m、14 m、16 m這七種水動力環境,借以探索不同水位差環境持續作用下覆蓋層中潛在的穩定土洞發育規模,以及臨界致塌水位差和極限土洞規模。 先分析在ΔH=16 m水動力環境持續作用下土洞逐漸擴展過程中模型滲流場、水力梯度、塑性區以及位移場情況。設置地表沉降監測點位于如圖2所示藍色圓點處,并記錄在ΔH=16 m水動力環境持續作用下土洞演化過程中地表監測沉降量,見圖4。 圖4 ΔH=16 m水動力環境持續作用下土洞演化過程中地表監測沉降量(uz)變化曲線 由圖4可見,土洞在剝蝕次數(Nslo)從第4次到第5次時,地表監測沉降量出現劇烈突變,說明在第5次土洞剝蝕后覆蓋層出現地面塌陷,而第4次土洞剝蝕后形成的土洞接近極限土洞規模大小。鑒于此,本次只展示前4次土洞演化過程中滲流場和力學響應的變化規律,見圖5和圖6。 由圖5可見:土洞演化過程中滲流場的流線主要向土洞中心匯聚,孔隙水向巖溶水補給,隨著土洞逐漸擴展演化,越靠近土洞總水頭越低[見圖5(a)];土洞演化過程中水力梯度小于臨界水力梯度的范圍基本不變(即覆蓋層中半圓形紅色圈定范圍),說明孔隙水位與巖溶水位之差ΔH一旦固定時,土洞擴展范圍也基本確定[見圖5(b)]。 圖5 ΔH=16 m水動力環境持續作用下土洞演化過程中滲流場和水力梯度的變化規律 由圖6可以進一步地直觀看出:土洞剝蝕后規模大小由最初的洞高1 m和洞寬3 m演變為洞高5 m和洞寬9 m的極限土洞規模,且隨著土洞的擴展演化,土洞周圍砂土層中塑性區范圍和塑性應變量逐漸增大,直到第4次剝蝕后塑性區擴展到砂土層頂部,即代表此時覆蓋層出現大面積塑性破壞[見圖6(a)];初始土洞形成后無論地表還是土洞周圍位移都較小,而當土洞逐漸擴展,地表和土洞周邊位移都顯著增大[見圖6(b)],但從圖6(b)中代表位移矢量方向的紅色箭頭線可知,地表主要以水平位移為主,而土洞中心線附近則以垂直位移為主,這能夠較好地解釋實際塌陷坑周邊出現拉裂縫且塌陷坑中心豎直沉降量最大這一現象。 圖6 ΔH=16 m水動力環境持續作用下土洞演化過程中塑性區和位移場的變化規律 以上僅從ΔH=16 m水動力環境條件下土洞演化過程及塌陷機理進行闡述,而在不同水位差水動力環境下土洞演化過程如圖7所示,圖中僅展示了模型x=40 m到x=60 m、z=3 m到z=13 m的局部塑性區發展情況[見圖7(a)至圖7(l)]及其對應穩定土洞規模和地表監測沉降曲線[見圖7(m)]。其中,w代表土洞洞寬(m);h代表土洞洞高(m);uz代表地表中心監測沉降量(m)。 圖7 不同水位差水動力環境下土洞演化過程中塑性區及其對應穩定土洞規模和地表監測沉降曲線 由圖7(a)至圖7(l)可見:當水位差ΔH在4~8 m時,土洞保持初始土洞大小并未擴展,說明在此水動力環境下砂性土層水力梯度I超過臨界水力梯度(Ibs=0.5)的范圍較小,沒有土層單元被剝蝕;而當水位差ΔH穩定在10 m時,土洞發生剝蝕而擴展至洞高3 m和洞寬5 m,塑性變形也有所增加;同樣地,當水位差ΔH穩定在12 m和14 m時,土洞剝蝕后形成的穩定土洞規模相應變大;當水位差ΔH為14 m水動力環境下土洞最終并未出現塌陷現象,即沒有出現類似如圖4所示的地表監測沉降量突變或計算不收斂的情況,這說明水位差ΔH需要達到16 m左右(即塌陷臨界水位差為16 m),才可能出現最終塌陷現象。 由圖7(m)可以看出:土洞洞寬曲線斜率總體大于洞高曲線斜率,說明土洞演化過程中洞寬擴展速率大于洞高擴展速率;地表監測沉降量隨著水位差ΔH增加而增加,地表沉降速率大致也可分為三個階段,即①當ΔH=4~8 m時地表沉降速率最小,②當ΔH=8~12 m時地表沉降速率居中,③當ΔH=12~16 m時地表沉降速率最大,說明地表沉降速率會隨水位差所處范圍不同而不同,水位差越大,地表沉降速率越大。 (7) 本文基于覆蓋型巖溶塌陷動態演化數值模型預測的土洞極限洞高相對普氏平衡拱理論求解的土洞極限洞高偏小,其原因在于普氏平衡拱理論的致塌力只有自重作用,而本文數值模型中考慮了滲透力和自重的聯合作用,使得在相對較小的土洞規模下仍會產生失穩破壞。 本文結合彈塑性理論和變飽和滲流理論,以臨界水力梯度為土洞剝蝕判據,提出了覆蓋型巖溶塌陷動態演化數值模型,探索了在不同孔隙水位與巖溶水位之差水動力環境下覆蓋層中潛在土洞的發育規模,并加以驗證,得出如下結論: (1) 在孔隙水位與巖溶水位之差ΔH小于8 m的水動力環境持續作用下,土洞將保持較小規模而不會進一步擴展;而當水位差ΔH超過8 m后將存在土洞剝蝕現象,且水位差越大,最終形成的土洞規模越大。 (2) 當水位差ΔH達到16 m的臨界水位差時,土洞將逐步剝蝕至產生塌陷,其極限土洞規模為洞高5 m和洞寬9 m,比基于普氏平衡拱理論預測的土洞規模偏小,其誤差為15%。 (3) 覆蓋型巖溶塌陷動態演化數值模型能夠較好地模擬土洞擴展演化及其失穩塌陷過程,可定量解釋覆蓋型巖溶塌陷的潛蝕—滲壓—自重致塌模式。2 不同水動力環境下土洞發育規模預測

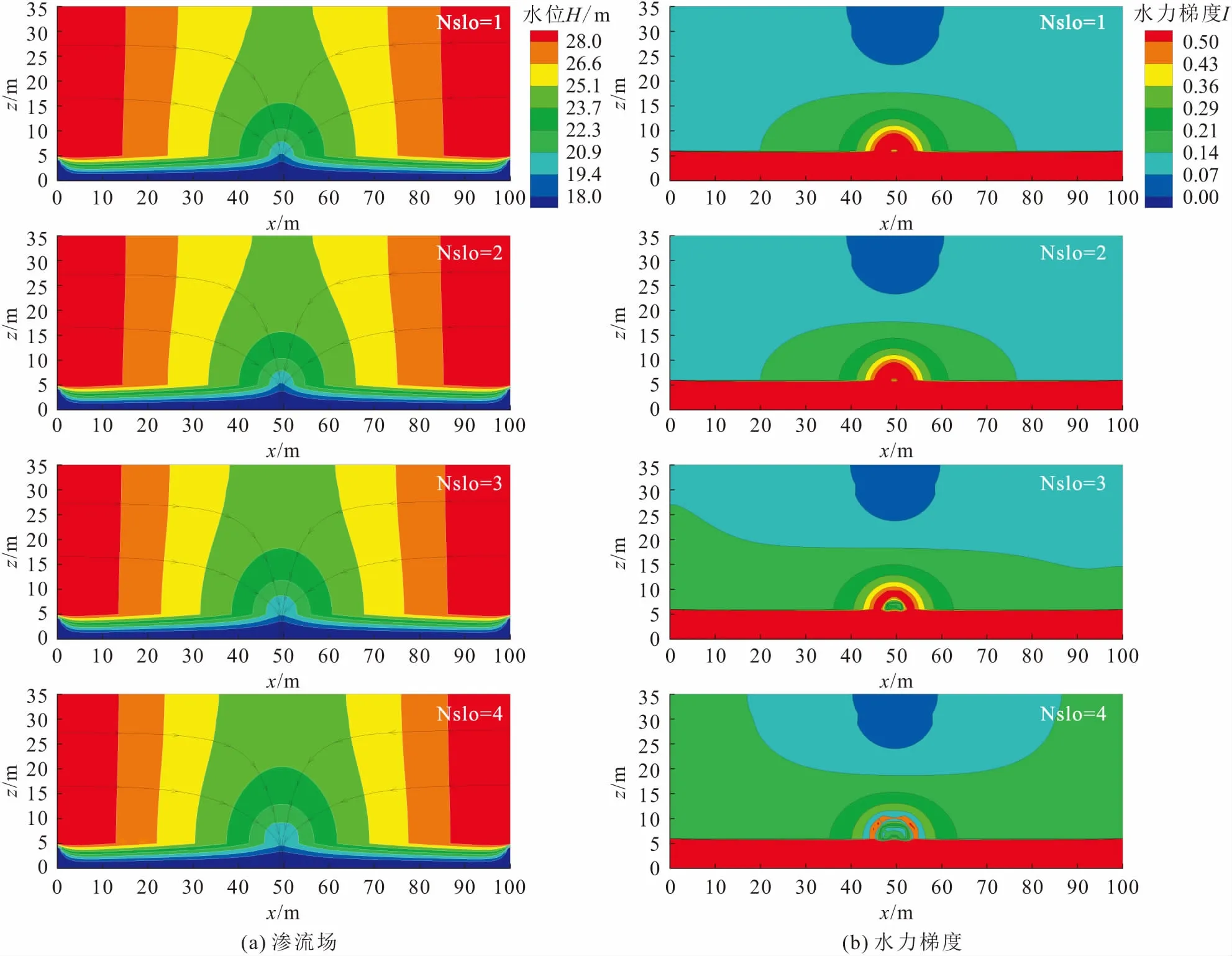
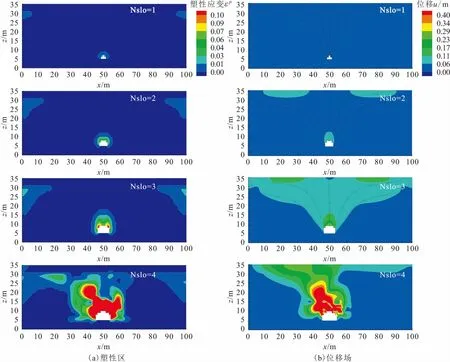

3 土洞預測結果驗證

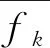
4 結 論

