非洲豬瘟舍內傳播元胞自動機仿真研究
楊婷婷, 薄興野, 田晶, 邵家源, 劉振宇*
(1.山西農業大學信息科學與工程學院, 太谷 030801; 2.山西農業大學農業工程學院, 太谷 030801)
非洲豬瘟病毒在豬只之間的傳播,主要與畜禽舍環境的溫度和濕度等相關因素有關。爆發地大多分布于北方[1]。每年年初是非洲豬瘟爆發的高峰期,爆發特點具有聚集性[2]。畜禽舍內豬只直接接觸是其傳播的主要途徑,具體包括豬只之間進行口鼻接觸、共同飲食、空氣傳播等,空氣傳播一般不超過2 m,豬只間保持安全距離,可減少感染[3]。急性非洲豬瘟通常會集中發生,且致死率極高,從患病到死亡的時間非常的短,往往不超過2 d,同時還未研發出可治療的藥物和有效的疫苗[4]。
針對傳染病的研究,目前大多都是使用單一的傳染病模型來進行分析。唐雄[5]從SIR(susceptible-infective-removed)模型的動力學行為作為研究,得出了傳染病在傳播過程中得以控制的條件。常見的傳染病模型,建立在微分方程之上,雖然計算方便,但存在很大的缺陷[6-10]。針對傳染病在畜禽舍內真實傳播過程中,一些隨機發生的事件,不能進行很好的處理。復雜的計算與現實畜禽舍內,豬只的接觸產生的隨機事件,不能很好地結合。因此單純使用傳染病模型模擬傳染病的傳播過程存在明顯不足,忽略了很多局部存在的個體特性[11]。
隨著技術的發展,大量的仿真與數學計算為傳染病(如非洲豬瘟)的模擬仿真提供了有利條件。目前,元胞自動機已被廣泛應用于人群擴散[12]、魚群行為預測[13]、線路規劃[14]、新冠病毒傳播模型的建立[15],驗證了元胞自動機在行為移動預測方面的真實性。
非洲豬瘟自傳入中國以來,對養豬業和食品安全等相關行業,產生了嚴重的不良影響[16]。因此,研究非洲豬瘟的傳染規律,進行仿真研究,當非洲豬瘟在養殖環境中爆發之后,能夠根據其預測結果,對病毒進行有效的防控。現使用元胞自動機,考慮非洲豬瘟傳染病的隨機性,將元胞自動機與傳統SI(susceptible-infected)模型相結合,對非洲豬瘟傳染病的傳播情況進行仿真分析,以期為相關傳染病的仿真研究提供理論指導。
1 研究方法
1.1 非洲豬瘟傳染模型選擇
非洲豬瘟在密閉豬舍內的傳播特征為,豬只個體數量少,傳染目標明確,與預期的效果相符。非洲豬瘟傳染病的特性:發病時間短,患病到死亡時間極端,而且暫無有效疫苗的研發,因此不存在治愈者。傳染病模型包括:SI、SIR、SEIR(susceptible-exposed-infective-removed)等,結合非洲豬瘟傳染病的特性,因為非洲豬瘟發病時間極端,所以不考慮E潛伏豬只的可能,即接觸過感染豬只但暫無傳染性的豬,而是全部都用易感豬代替,而SEIR多用于惡性傳染病,且潛伏期對于整個傳染周期較長。而對于致死率相對高的的傳染病,大多感染后就會死亡,不存在治愈的情況,R治愈豬只假設為不存在。因此針對非洲豬瘟選用SI模型,相比較更為合適。該模型是一個單向模型,隨著時間的推移,易感豬只數會逐漸向感染豬只數輸入,最終易感豬只數都會降為 0,所有均變成患病豬。這也是SI模型的局限性,因此該模型不適用于傳播周期長和有疫苗研發成功的的傳染病,但適合與非洲豬瘟傳染病的研究。因此,在其理論研究基礎上,基于動力學理論,建立非洲豬瘟傳播的動力學SI模型,并計算模型的解。通過非洲豬瘟傳染病模型的構建與仿真,發現對控制和管理非洲豬瘟的傳播起了重要作用。
1.2 模型的構建
對SI模型建立的基本假設。首先,假設已知的數據具有真實性,對于豬只的出生、死亡等情況不進行考慮,設定該豬舍內的豬只總數為Ntotal。其次,將該模型簡單的分為易感豬只S和感染豬I,其模型傳播機理如圖1所示,SI模型的感染規則[17]。最后,假設豬只不可流動,即無豬只流入和流出該豬舍,因為不需要考慮了感染畜禽治愈后獲得免疫能力的情況和接種疫苗后的治愈行為。
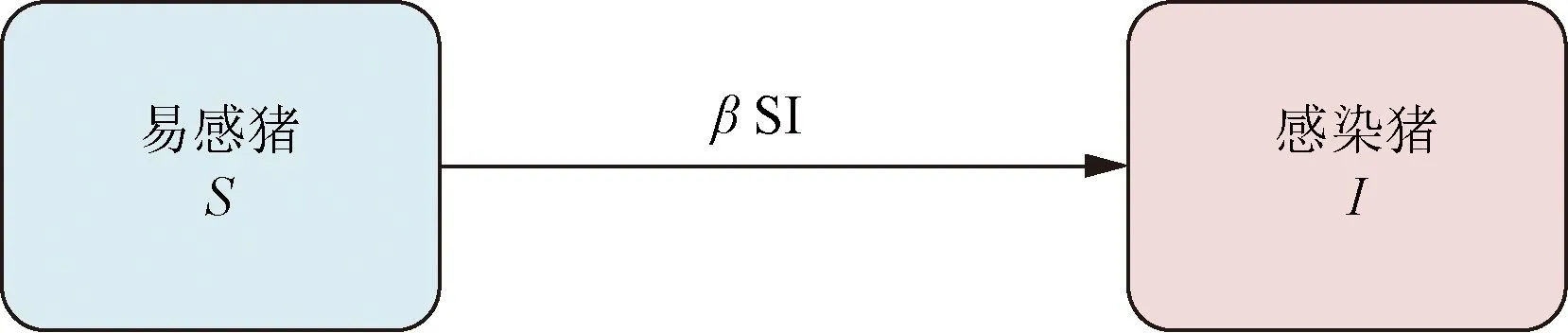
圖1 SI模型Fig.1 SI model
圖1中,S為易感類,該類豬只沒有免疫能力,當符合感染情況,過度接觸時,有一定的概率染上該豬瘟;I為感染類,該類豬只以及為患病豬,具有一定的概率把該病毒傳染給易感豬只;β為易感豬只被患病豬感染的概率。
假設總畜禽數不變,比例系數不變。在初始狀態時,設置一個或者多個為感染豬只。在單位時間內,當易感豬只和感染豬只發生接觸行為,易感豬只就會以概率為β的可能性轉變成感染豬只。t時刻易感豬只占總數的比例為S(t),感染豬只占總數的比例為I(t),兩者的關系可表示為
S(t)+I(t)=1
(1)
該模型是一個單向模型,隨著時間的推移,易感豬只數會逐漸向感染豬只數輸入,最終易感豬只數都會降為0,所有均變成患病豬。
1.3 異質性
在現實生活中,豬只感染的概率與環境、群體數量、季節變化等相關因素之間存在一定的聯系。因此需要對不同的元胞,設置參數不同的感染系數,從而使模擬的畜禽舍傳染過程考慮到了群體的異質性[18]。根據不同豬只個體體質的考慮,設計抵抗能力測算值Ri,j;對患病后豬只的運動情況的分析,設計不同的傳染能力fi,j,以上即為個體間存在異質性[19]。
典型的SI模型的微分方程在計算的過程中,并沒有考慮豬只的個體異質性,每個豬只都有相同的概率感染非洲豬瘟病毒。結合豬只具有異質性這一特點,針對不同因素進行全面的考慮,引入距離影響因子[式(2)],進而推導計算出豬只間通過有效接觸而引發的傳染概率Pi,j[式(5)]。
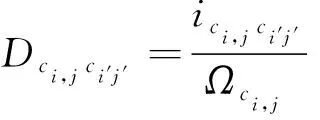
(2)

(3)
(4)
式中:Dci,jci′j′為距離影響因子;i和j為豬只移動前的坐標;i′和j′為豬只移動后的坐標;ci,j為感染概率計算豬只即中心元胞;ci′,j′為豬只8個方向的任一鄰居豬只;Nci,j為中心豬只的摩爾鄰居內所有鄰居豬只的集合。
綜上所述,定義為中心元胞的豬只ci,j的有效接觸感染概率為Pi,j,Pi,j值越大,說明越容易感染非洲豬瘟。
(5)
式(5)中:fi,j為個體的感染能力;Ri,j為個體的抵抗能力。
從式(5)可以看出,在具有傳染病的豬舍內,不同的豬只感染病毒的概率與距離、具體病毒的傳染力以及個體本身的抵抗能力3個值相關。
1.4 演化規則
演化規則為元胞自動機進行演化分析的核心[20],狀態轉移函數f可表示為
(6)
式(6)中:
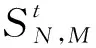
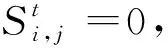
系統時間記錄的基本單位為天數,記錄元胞此刻的存在狀態,在演化過程中,關于具體元胞在系統內的移動性描述也是一個模型成功與否的關鍵因素,結合對豬舍內豬只活動范圍的觀察,在忽略外界干預的情況下,豬舍內豬只的移動是隨機的,因此對豬只移動規則進行設計,因此本模型采用的是隨機移動步長的方式。
1.4.1 豬只移動與感知范圍
元胞關系為Moore型鄰元關系,圖2所示的摩爾鄰居即為豬舍內的豬只移動范圍。

圖2 元胞(i,j)的摩爾鄰居Fig.2 Moore neighbor of cell (i, j)
系統將所模擬的豬舍進行網格劃分,即劃分為M×N個相同大小的網格,網格元胞拼接即為模擬的豬舍的二維空間。設定每個元胞都屬于,設施(即畜禽舍的墻面和圍欄)、個體(豬只個體本身)、空白區域(豬舍可活動區域),這3種屬性特征的其中一種。因此,對于任意位置(xi,yi)元胞表示的豬只,元胞狀態集合Scell的表現形式為
Scell=(xi,yi,Ui,j,ui,j,vi,j)
(7)
式(7)中:Ui,j、ui,j、vi,j分別為豬只在舍內、向x軸移動時的速度、y軸移動時的速度,m/s。
1.4.2 模型移動行為假設
(1)避開豬舍內設施移動。除空白活動區域外,墻體圍欄等設施以及豬只個體,都為不可活動的網格,因此豬只發現到會與墻體等發生碰撞的時候,會自覺地轉換移動方向。
(2)空白區域隨意移動行為。該模型不考慮豬只的行為的其他故意干擾等影響因素,因此豬只在豬舍內的運動為隨機活動,摩爾鄰居的各個方向都有一定的概率,而且速度等因素也不受控制
(3)優先向目視范圍移動。一般豬比較習慣向自己目光所視方向移動,因此豬具有相當大的概率向可以看到的范圍為移動,而非背后。
1.4.3 豬只移動規則
豬只在豬舍內的移動規則,通過計算向不同的方向的權重值,進而得到移動的概率,確定Agent下一步移動的網格[21]。具體的移動方向如圖3所示。
Agent向K方向移動的概率計算公式為
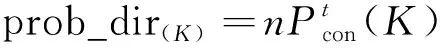
(8)


1~8表示方向圖3 Agent運動方向Fig.3 Agent in the direction of motion
豬只不同方向網格的引力概率的計算公式為
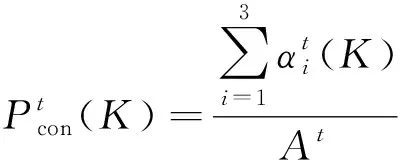
(9)
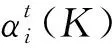
(1)避開豬舍內設施移動的表達式為
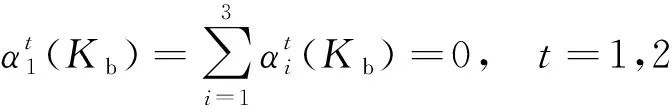
(10)
式(10)中:Kb為放置有設施的方向。
(2)空白區域隨意移動行為,模型中表示為豬只擁有向各個方向運動的概率,可表示為
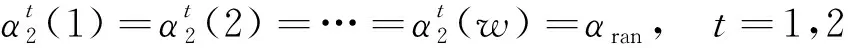
(11)
式(11)中:w為可能的移動方向;αran為w方向的吸引權重。
(3)優先向目視范圍移動,豬具有相當大的概率向可以看到的范圍為移動,其表達式為
(12)
式(12)中:Ksee為豬只的前方可視范圍的網格方向;αsee為可視范圍的網格吸引力權重值。
1.5 算法過程描述
步驟1使生成的豬只元胞,離散的處于代表豬舍的元胞空間內。首先設定所有的豬只元胞狀態為0。然后隨機在這些元胞中,設定一定數量的感染豬只,這些元胞的狀態為1,初始設定數目不易過大,否則不能很好的模擬非洲豬瘟在畜禽舍內的傳播過程。
步驟2設定元胞在空間中的最大移動步長為dmax。從系統模擬的迭代天數d=0時刻開始,每更新一次,都需要對系統中所有元胞的狀態進行掃描與統計。同時,隨機選擇一定的元胞模擬其在畜禽舍內的具體移動,標記選擇的元胞坐標為(i,j),然后根據移動規則和各個方向的吸引權重因子,計算向周圍各個方向移動的最大值,得出移動的具體方向,即移動距離(di,dj)進行移動,交換后坐標為(i,j)和(i+di,j+dj)的兩個元胞,表示元胞發生了一次移動。
步驟3獲取每個時刻豬只元胞的狀態,然后判斷其是否為易感元胞,如果為易感元胞,再判斷其周圍是否存在感染元胞,并計算該易感元胞的具體感染概率值,再與規定的感染閾值X進行比較,如果X 步驟4如果步驟3中的被選元胞不是易感元胞,判斷是否為感染元胞。如果是,則不進行任何的改變,該元胞的狀態值保持不變,并且一直具有傳染能力。 步驟5對元胞空間內所有的元胞進行掃描,隨著系統的演化,不斷地更新每個元胞的狀態后,判斷元胞自動機是否達到特定的狀態,即穩定狀態,當所有的元胞都變為感染元胞,仿真過程正式結束,否則跳轉到步驟2重新選擇元胞。 按照豬場設計相關規范,來設計豬舍內非洲豬瘟的傳播模型。實驗地點為晉中市太谷區范村鎮北里村,東方希望養豬場,研究豬舍為育肥豬舍。模型的具體尺寸為:豬場長20 m、寬5 m,由10個大小相同的隔間組成,單個隔間的室寬為2 m、長為 4 m。不同隔間內豬只的具體數量為6~10頭。豬舍的3D幾何模型如圖4所示。 圖4 豬場幾何模型Fig.4 Geometric model of pig farm 仿真研究嚴格按照豬場物理模型進行模擬,通過對實地豬場的豬只飼養數量、活動情況、接觸數量等進行實地的調查與試驗進行設計。 不同傳染強度的非洲豬瘟傳染病,具體的元胞機設計也有所不同。首先,針對不同系統區域,設定不同元胞個數,來模擬養殖密度不同的豬舍隔間,方便觀察非洲豬瘟在豬舍內的不同密度的豬舍的感染情況。其次,根據分析要求,系統初始患病豬只數為隨機生成的極少個數。然后演化系統內的整體環境為豬只個體位于該離散系統的不同位置,并且按照設定的離散時間進行輪次,在規定范圍內按照設定的移動規則進行移動。具體設計用四元組表示豬舍系統,即 A=(Ld,Scell,Nmoore,F) (13) 式(13)中:A為模擬的整個豬舍系統;Ld為二維元胞空間網格的規模,設定為100×100的二維圖,假設的元胞個數為10 000個。但是并不是所有的元胞都表示為豬舍內的豬只個體;Scell為元胞狀態集合;Nmoore為豬只的摩爾鄰居;F為豬只的感染和移動規則,即豬只狀態轉換函數。 假設該系統為不受其他外界因素影響的封閉的畜禽舍,不設置治愈率,感染后即為患病豬。當健康豬只在系統移動過程中到達了新的位置后,遇到了另一只患病畜豬,不同的豬只傳染病的傳染性不同,根據豬只個體的異質性,計算不同的感染概率。每只畜禽都有概率被傳染,或者去傳染臨近的其他鄰居元胞。 通過對比,分析元胞自動機對非洲豬瘟傳播的仿真模擬數據與原始SI模型傳播數據的擬合性。圖5為使用元胞自動機對非洲豬瘟自由傳播情況下的仿真結果。其中,可視圖的x、y坐標大小分別設置為100、100,模擬整體豬場,小隔間的x、y大小分別為40、40,數量為10個,走廊大小設置為20、100,長度與實現選擇的豬場大小的長度比為 10∶100,寬度為5∶100,與實際豬場構造擬合度較高;小隔間內自動生產的豬只數目為2~11個,符合實際豬場平均隔間豬只數2~10只的數量。通過觀察可以發現,豬只每迭代一次的移動范圍在隔間內,與現實豬只的分欄飼養相符。結果表明:元胞自動機仿真研究與現場豬舍較吻合,符合試驗要求。 非洲豬瘟爆發初期,即模擬的迭代天數為1 d時[圖5(a)],豬舍內感染非洲豬瘟的豬只為4頭,感染率約為5%,此結果與SI模型模擬的第1~7.8天的感染數據(圖6)一致。 D為模擬的迭代天數,d圖5 自由傳播情況仿真結果Fig.5 Simulation results for the free propagation case 當模擬的迭代天數為10 d時[圖5(b)],此時的感染豬只為21頭,當模擬的迭代天數為15 d時[圖5(c)],此時的感染豬只高達69頭。在模擬的天數為10~15 d的時期增長率最高,與SI模型I=Ntotal/2時(圖6),即感染豬只數目到達半左右時的,增長速率基本一致,都在較短的時間實現了大量的傳播。 當模擬的迭代天數為50 d時[圖5(d)],豬舍內非洲豬瘟的感染率接近99%,只有一頭未染病豬只,其余基本全部感染,但相比模擬的迭代天數為15 d時的感染情況,增長趨于緩慢,此結果與SI模型(圖6),第20天后數據趨于平穩的結果一致。 通過對比兩種模型的仿真結果(圖7)可知,當易感豬只全部轉化為感染豬只時SI模型d=13.8,元胞自動機迭代為d=14.3。擬合度為0.96。隨著時間的推移,感染豬只增長速率為:先快速上升再緩慢下降。SI模型有兩個主要結論:①指數增長率r=βNtotal,其中,Ntotal為豬舍內養殖總數,即增長率與養殖總數成正比;②在I=Ntotal/2 時,I增加得最快,之后趨于平穩。 圖6 SI模型傳播數據Fig.6 SI model propagation data 圖7 SI模型與CA模型傳播數據對比擬合Fig.7 SI model compared the propagation data with the CA model 分析可知,元胞自動機對非洲豬瘟傳播的仿真模擬與SI模型的數據能夠實現較好的擬合,并且精確度優于傳統的SI模型,可以更直觀的看到具體的傳播情況。 傳統的SI模型,只是對于非洲豬瘟爆發后感染豬只數量進行預測計算,使用元胞自動機可以更好的對演化過程進行可視化的顯示,通過迭代預測豬只個體在豬舍內的活動,以及模擬非洲豬瘟隨著豬只的移動的傳播情況,對傳播過程與結果進行預測。 通過設計在封閉畜禽舍系統中,豬只感染非洲豬瘟傳染性疾病后傳播問題的仿真分析,得出如下結論。 (1)環境因素和豬個體體質的差異,使每只豬被感染的概率是不同的,因此引入了距離影響因子。通過計算可知,易感豬只感染的概率與個體的感染能力、個體的抵抗能力及距離因子有關。 (2)考慮豬舍內豬只的移動規則,建立的模型能夠模擬,避開豬舍內設施移動、空白區域隨意移動行為和目視范圍移動3種行為模式,模擬結果能夠體現豬的運動特征具有隨機性。 (3)進行元胞自動機仿真試驗,仿真結果與SI模型及實際情況下的傳播數據,進行對比擬合,擬合度為0.96。結果表明:元胞自動機對非洲豬瘟的仿真結果與實際情況相符,且模擬精度更高。 (4)與傳統的傳染病SI模型相比,使用元胞自動機具有更好的預測性,具體包括可以更好的觀察非洲豬瘟在豬舍的具體傳播情況,以及對非洲豬瘟傳染病的演化過程可視化。可根據仿真結果,更好的分析預測的傳播數據,進而選擇適當的控制策略實現非洲豬瘟的有效控制。2 元胞自動機仿真設計
2.1 物理模型的設計
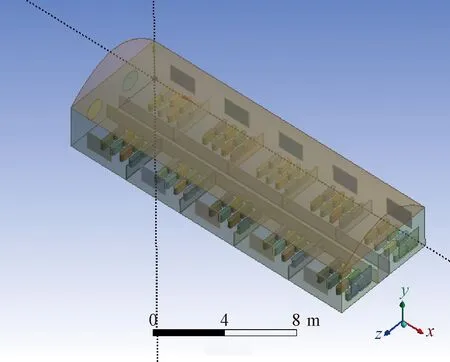
2.2 數據假設
3 結果與討論
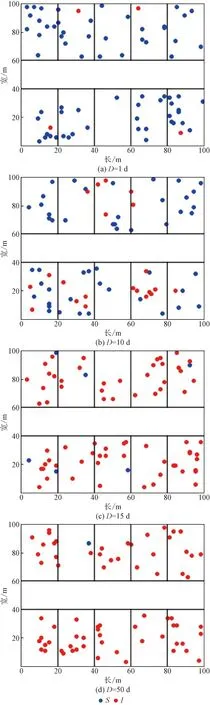


4 結論

