波在分數Maxwell流體飽和孔隙介質界面的反射和透射

張秀娥， 康永剛

(防災科技學院基礎課教學部， 三河 065201)

研究彈性波在含流體孔隙介質中的傳播，可以為油氣儲層、飽和及非飽和土、海底沉積物等介質的勘探提供理論基礎。Biot[1-3]在建立該類介質波動方程時，首先分開考慮孔隙流體和固體骨架的運動，他的理論是該領域的開創性工作。之后被提出的重要模型有噴射流模型、Biot理論與噴射流相結合的(Biot squirt, BISQ)模型、飽和斑塊模型、層狀周期模型和雙孔隙模型等[4]。這些理論都針對充滿牛頓流體的孔隙介質，但實際孔隙流體經常表現出非牛頓流體特性，如油藏開發領域涉及的重油、頁巖油、瀝青油等高黏度原油[5]，當作牛頓流體計算的頻散和衰減曲線，往往與實驗結果存在較大的差距。Tsiklauri等[6]通過對黏滯系數引入一個修正因子，考察了彈性波在Maxwell流體飽和孔隙介質的頻散和衰減特性。Cui等[7]在引入黏滯系數修正因子時，考慮了孔隙的尺寸分布。崔志文等[8]在BISQ模型中考慮了非牛頓流體的影響。Markov[9]研究了Maxwell流體飽和孔隙介質表面的Rayleigh波。Revil等[10]在研究震電效應時考慮了流體的非牛頓效應。劉文山等[11]使用動態黏度表征非牛頓流體的特征，但仍然是基于經典的Maxwell流體。Solazzi等[12]研究了彈性波在Maxwell流體飽和孔隙介質中傳播時的噴射流效應。El Baroudi等[13]討論了Maxwell流體飽和孔隙夾層中傳播的洛夫波(Love wave)。以上研究表明，孔隙流體的非牛頓效應對彈性波的傳播有重要影響。分數階微積分已被成功應用到許多領域，如孔隙介質中的反常滲流[14]，但在孔隙介質的彈性波領域，相關研究很少。熊繁升[15]在建立孔隙介質波動方程時引入了分數階導數描述的耗散函數。利用分數階導數描述的分數Maxwell流體，更適合描述實際非牛頓流體的特征，但尚未發現在孔隙介質彈性波領域考慮該類流體的研究。

通過分析彈性波在含流體的孔隙介質界面上的反射和透射特征，可以獲取該類介質的相關信息。Stoll等[16]、李堯等[17]研究了流體/流體飽和多孔介質界面上的反射與透射，應用了包含噴射流機制的BISQ模型。魏征等[18]、Sharma等[19]、Tomar等[20]研究了固體/流體飽和多孔介質邊界上的反射與透射, 其中，魏征等[18]研究的是橫觀各向同性孔隙介質，而Sharma等[19]、Tomar等[20]考慮了孔隙介質含兩種互不相容流體的情況。Wu[21]、代智軍等[22]、Singh等[23]研究了液體飽和多孔介質/液體飽和多孔介質界面上的反射與透射, 其中代智軍等[22]采用了雙孔隙模型。還有學者研究了彈性波在含孔隙介質復雜結構的反射和透射，如三明治結構液體/孔隙介質/固體[24]、固體/孔隙介質/固體[25]等。以上研究認為，孔隙介質充滿牛頓流體，目前尚未發現在反射和透射現象中考慮非牛頓流體的情況。

含流體的孔隙介質為耗散介質，傳播的一般是非均勻波，目前的研究都基于均勻波，與實際情況并不符合。研究彈性波在孔隙介質界面反射和透射時，會采用Snell定理，即各列波在x方向(假設x方向在入射面內且沿著分界面)波數相等。基于均勻波假設，應用Snell定理會給出復數的三角函數和角度，物理意義不明確。例如，波由彈性介質射向孔隙介質時，入射角和入射波在x方向波數均為實數，由于孔隙介質中波數為復數，要求透射角的正弦為復數(即透射角為復數)，來保證二者乘積為實數。

鑒于此，通過對分數Maxwell流體在圓管內的振蕩流分析，給出黏滯系數修正因子，由此來表示非牛頓流體對孔隙介質彈性波的影響。推導了波從彈性固體射向孔隙介質時，在兩個半空間分界面的反射和透射系數。按照非均勻波討論，給出的透射角為實數，物理意義明確。通過數值算例，并與牛頓流體的情況對比，討論了孔隙流體非牛頓效應對反射和透射系數的影響。最后部分給出一些重要結論。

1 控制方程

1.1 Biot理論

Biot理論給出的流體飽和孔隙介質的應力-應變關系為[3, 16]

τij=(H-2μ)eδij+2μεij-Cζδij

(1)

pf=Mζ-Ce

(2)

H=(1-Kb/Kr)2M+Kb+4μ/3

(3)

C=(1-Kb/Kr)M

(4)

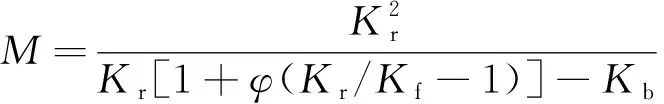
(5)

式中：Kb、Kr和Kf分別為骨架、固相和孔隙流體的體積模量。

Biot理論給出的運動方程為

(6)

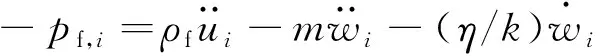
(7)

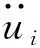
將式(1)、式(2)代入式(6)、式(7)，得到彈性波的動力學方程為

(8)

(9)

1.2 分數Maxwell流體的影響

當流體在圓管中流動，管壁按時間規律e-iωt沿縱向振動，其中，t為時間，ω為圓頻率，i為虛數單位。對于柱坐標系(r,θ,z)，r和θ分別為極徑和極角。流體只沿著z方向流動，vf為流速，vf為流速大小，即vf=vf(r,t)ez，其中ez為軸向的單位矢量。此時只有應力τrz不為零，動量方程為

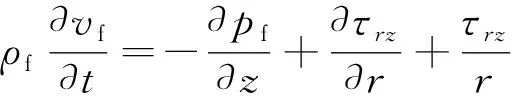
(10)

考慮到物理量都按e-iωt規律隨時間變化，式(10)可改寫為

(11)

分數Maxwell流體的本構關系為[26]

(12)

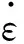
當tm=0時退化為牛頓流體，當γ=1時為經典的Maxwell流體。保留式(12)中應變對時間的一階導數，分數Maxwell模型才表現出流體的性質。分數階導數有不同形式的定義，采用Riemann-Liouville定義，積分下限取為負無窮[27]，即

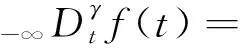
0<γ<1

(13)

當流體在圓管中流動，管壁按時間規律e-iωt沿縱向振動，式(12)變為

(14)

式(14)中：τrz為管壁應力。

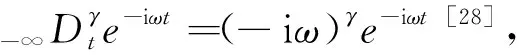
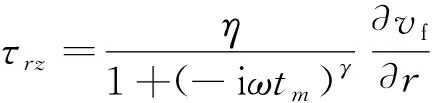
(15)

引入相對速度v1(r,t)=vf(r,t)-vs，其中vs為管壁的速度。將式(15)代入式(11)得

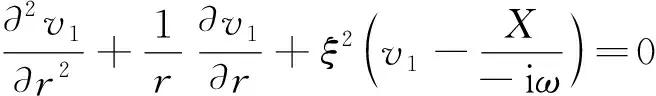
(16)

式(16)中：

(17)

ξ2=iωρf(1+(-iωtm)γ]/η

(18)

令a為圓筒半徑，由非滑移邊界條件v1(a,ω)=0，得

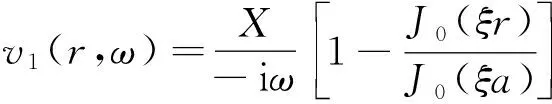
(19)

式(19)中：J0為零階貝塞爾函數。

仿照Biot[2]的做法，圓管截面的平均流速可表示為

(20)

式(20)中：J1為一階貝塞爾函數。

將式(19)代入式(15)得管壁的應力為

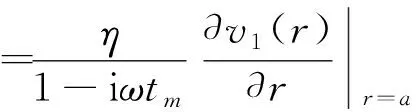
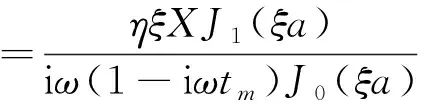
(21)

計算總摩擦力與平均流速的比值

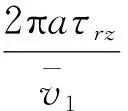
=-8πηF(κ)

(22)

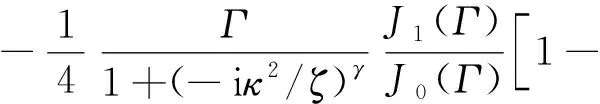
(23)

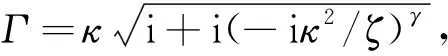
當γ=1時，式(23)退化為Tsiklauri等[6]的結果。分數階導數模型，多了參數γ，相對于經典的Maxwell模型，更適合對實際非牛頓流體的描述。由式(22)可知，為了表示孔隙流體的非牛頓效應，只需用F(κ)η代替η。

由此，式(9)變為

(24)

為了求解式(8)和式(24)，對位移進行亥姆霍茲分解

(25)

(26)

式中：φ和ψ分別為標量勢和矢量勢；下標s為固體骨架；下標f為孔隙流體。

將式(25)、式(26)代入式(8)和式(24)，可求得快縱波波數lp1、慢縱波波數lp2和橫波波數ls，具體求解過程可參考文獻[16]，在此不再贅述。可求得流體與骨架勢函數的幅值比

(27)

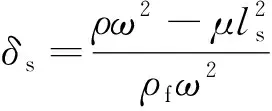
(28)

式中：δp1、δp2和δs分別為流體中P1波、P2波和S波與骨架中相應波的幅值比。

式(27)和式(28)說明同一種波在骨架和流體中引起不同幅值的振動，印證了Biot關于流體與骨架間存在相對運動的假設。

2 反射和透射

彈性固體半空間的彈性波控制方程為

(29)

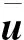
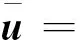
(30)

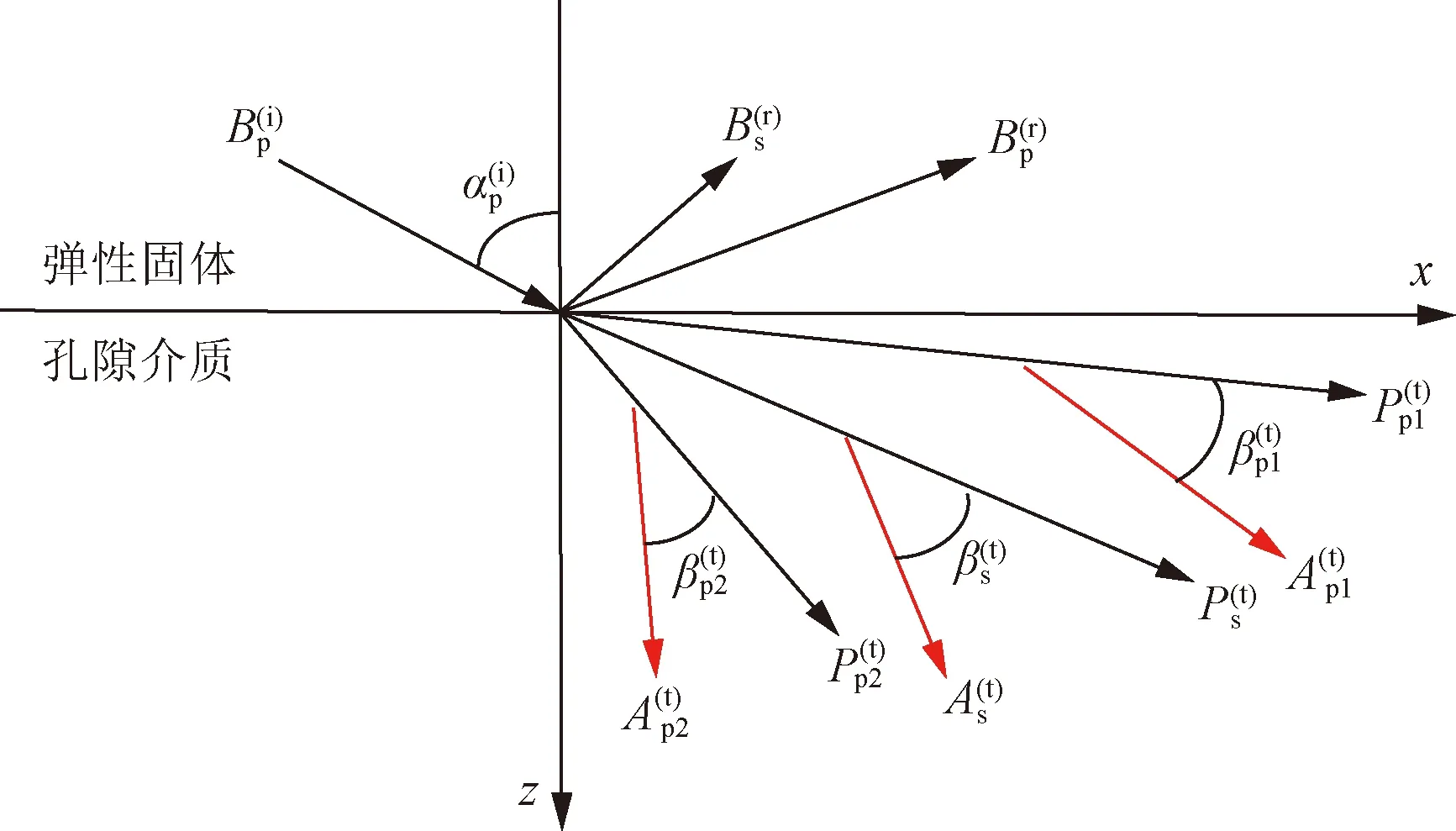
P為傳播矢量；和分別為P1波、P2波和S波的透射角；A為衰減矢量；β為傳播矢量與衰減矢量間的夾角；即上標i、r和t分別表示入射波、反射波和透射波；下標p、s、p1和p2分 別表示P波、S波、 快縱波(P1)和慢縱波(P2)圖1 波在彈性固體/孔隙介質界面的反射和透射Fig.1 Reflection and transmission of elastic waves at an interface between solid and porous medium

式(30)中：φ1和ψ1分別為標量勢和矢量勢。

P波和S波的波數分別為

(31)

2.1 反射和透射波的勢函數

彈性固體中的入射波和反射波用勢函數可表示為

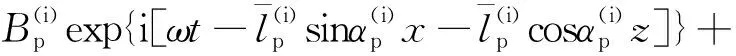
(32)

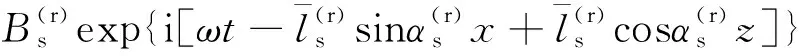
(33)

式中：B為幅值；上標i和r分別為入射波和反射波；下標p和s分別為P波和S波；矢量勢ψ1=ψ1i2，其中，ψ1為其大小，i2為沿y軸方向的單位矢量。

考慮流體和固體相對運動的孔隙介質是耗散介質，傳播的通常是非均勻波。目前，研究者們常按均勻波處理，與實際不符。此外，按均勻波處理，應用Snell定理會給出復數的角度，物理意義不明確。假設孔隙介質中傳播的是非均勻波，則透射波用勢函數可表示為

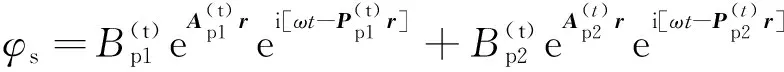
(34)

(35)

(36)

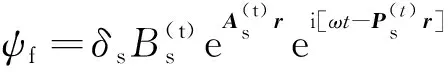
(37)

式中：B為幅值；上標t為透射波；下標p1和p2分別為快縱波和慢縱波；矢量勢ψs=ψsi2，ψf=ψfi2，ψs和ψf分別為ψs和ψf的大小；位置矢量r=xi1+zi3，其中單位矢量i1和i3分別沿x軸和z軸方向。

傳播矢量和衰減矢量可分別表示為

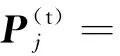
j=p1,p2,s

(38)

式(38)中：kj=kjR+kjIi和dj=djR+djIi分別為x、z方向的復波數，下標R和I分別表示實部和虛部，kj和dj滿足：

(39)

注意dj取復數平方根的主值，即djR≥0。利用傳播方向和衰減方向的夾角β，x方向的復波數可表示為

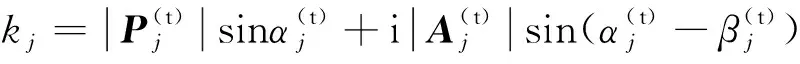
(40)

由Snell定理可知，各列波在x方向的波數相等，即

(41)

(42)

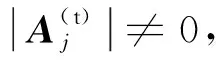
2.2 邊界條件

在界面z=0的連續性條件如下。

(1)彈性固體和孔隙介質骨架的法向位移連續，可表示為

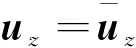
(43)

(2)對于非滲透界面，流體相對骨架的z方向位移為零，即

wz=0

(44)

對于滲透界面，有

pf=0

(45)

(3) 彈性固體和孔隙介質骨架的切向位移連續，可表示為

(46)

(4) 彈性固體和孔隙介質的正應力連續，可表示為

(47)

(5) 彈性固體和孔隙介質的切向應力連續，可表示為

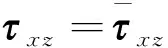
(48)

利用波的勢函數式(32)～式(37)和邊界條件式(43)～式(48)，反射和透射系數可由式(49)獲得

(49)

式(49)中：a為一個5×5的矩陣；b為一個列矩陣；上標T表示轉置矩陣。

式(49)中矩陣a的各元分素別為：

a13=-dp1,a14=-dp2,a15=-ksR。

對于不可滲界面有：a21=0,a22=0,a23=-δp1dp1,a24=-δp2dp2,a25=-δsksR。

對于可滲界面有：

矩陣b的各元素分別為：

3 數值算例和討論

圖2為德博拉數取值不同時，反射和透射系數隨頻率的變化曲線。低頻時，非牛頓效應對反射和透射系數幾乎沒有影響。隨著頻率的增加，非牛頓效應逐漸變得明顯，反射和透射系數隨頻率出現幅值衰減的振動。德博拉數ζ越小，與牛頓流體情況差別越大，振動幅度也越大。隨著德博拉數的變化，孔隙介質的性質改變，孔隙介質的固有頻率相應變化。當激振頻率接近固有頻率時，透射系數增大，反射系數相應減少。例如，當德博拉數為0.1時，在1 000～10 000 Hz范圍，孔隙介質存在多個固有頻率。因此P波反射系數和P1波透射系數在該頻率范圍出現周期性振動。

圖3為分數階導數的階數對反射和透射波的影響。隨著階數的增加，與牛頓流體的情況差別越來越大，并開始出現幅值衰減的振動。當γ=1時，即整數階Maxwell流體時，幅值振動最明顯。分數階導數的階數變化，孔隙介質的固有頻率變化。當一定頻率范圍內存在多個固有頻率時，每當激振頻率接近固有頻率，透射系數增大，反射系數減少，出現幅值隨頻率的振動。通過階數的變化，可以實現牛頓流體到Maxwell流體的過渡，擴大了模型的適用范圍。

圖4為黏滯系數對反射和透射系數的影響。由于德博拉數ζ=a2ρf/(ηtm)，相應改變ζ表示其他參數不變。低頻時，介質有足夠的時間達到松弛狀態，而高頻時，介質來不及松弛。所以，低頻和較高頻時，黏滯系數的影響可以忽略。黏滯系數越大，開始由低頻時的值向高頻時的值變化的頻率越大，似乎圖形在向高頻移動。振動的幅值也隨著黏滯系數的變化而有所不同。在中間頻率范圍，圖形隨黏滯系數增加向高頻的移動，反映了材料松弛時間隨黏滯系數的變化。

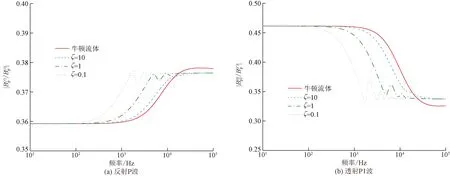
圖2 德博拉數不同時的反射和透射系數Fig.2 Reflection and transmission coefficients for different Deborah number

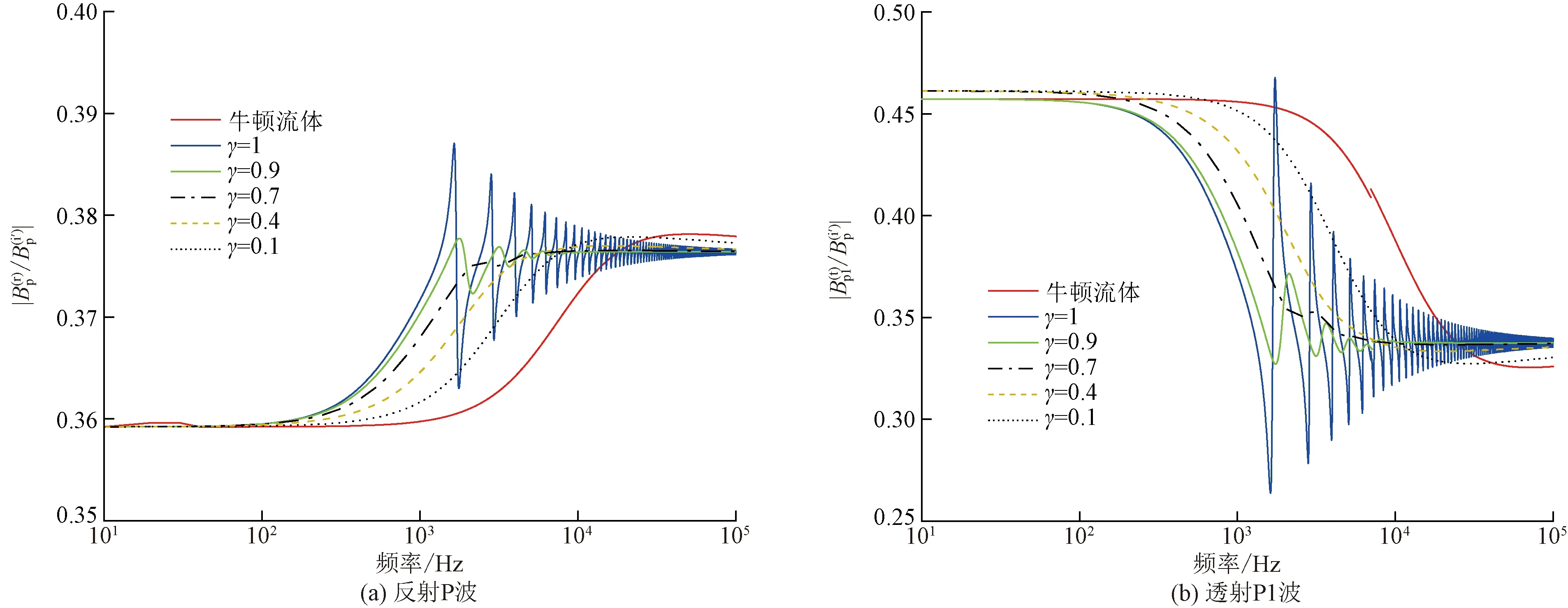
圖3 分數階導數的階數對反射和透射系數的影響Fig.3 Influence of the fractional index on reflection and transmission coefficients

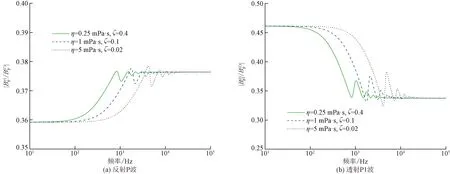
圖4 黏滯系數不同時的反射和透射系數Fig.4 Reflection and transmission coefficients for different viscosity (γ=0.9,

圖5為邊界滲透性對反射和透射系數的影響。無論牛頓流體還是分數Maxwell流體，邊界滲透性顯著影響能量在反射波和透射波間的分配比例。邊界可滲時，彈性波更易被反射。這是由于邊界不可滲時，流體阻抗導致了透射波的增強和反射波的減弱。

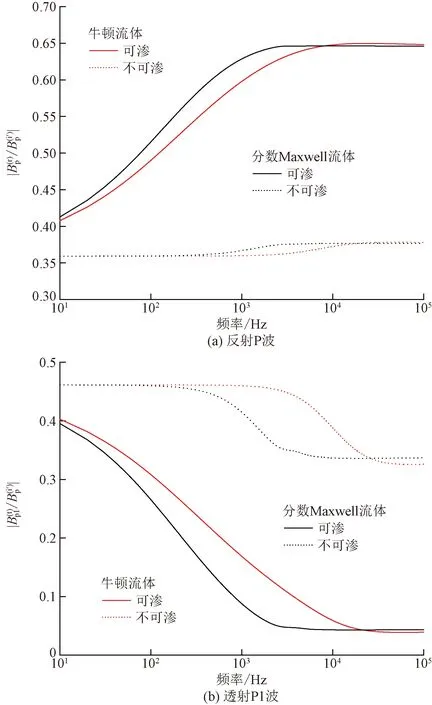
圖5 邊界條件對反射和透射系數的影響 Fig.5 Influence of the interface conditions on reflection and transmission coefficients (ζ=0.1, γ=0.6,

4 結論

通過對分數Maxwell流體在周期性振動圓管中流動的分析，給出黏滯系數修正因子，由此來表示孔隙流體非牛頓效應的影響。目前在孔隙介質彈性波領域常被討論的Maxwell流體為其特例。推導了平面P波從彈性固體射向孔隙介質時，在界面的幅值反射和透射系數，其中孔隙介質充滿分數 Maxwell 模型描述的非牛頓流體。按照非均勻波討論，由Snell定理給出的透射角為實數，物理意義明確。通過數值算例，并與充滿牛頓流體情況對比，研究了流體非牛頓效應對反射和透射系數的影響，得出如下主要結論。

(1)波在固體和孔隙介質的界面反射和透射時，孔隙介質中的快、慢縱波和橫波都是非均勻波，它們的傳播方向不同，但衰減方向相同，均垂直于界面。

(2)分數階模型架起了牛頓流體與Maxwell流體間的橋梁，增加了一個參數，擴大了非牛頓流體模型的使用范圍。

(3)德博拉數越小，分數Maxwell流體的非牛頓效應越明顯，反射和透射系數與牛頓流體情況的差別越大。德博拉數較小時，由于孔隙介質固有頻率的變化，會出現隨頻率的幅值衰減振動。

(4)黏滯系數、邊界的滲透性對反射和透射波均有影響。雖然表現特征有差異，但都主要影響中等頻率范圍。