考慮土體強度非均質和各向異性的隧道洞口仰坡地震穩定性上限解

張京伍, 榮耀, 李棟偉, 孫洋, 何昌春, 陳欣

(1.江西省交通科學研究院有限公司， 南昌 330200； 2. 東華理工大學土木與建筑工程學院， 南昌 330013；3.蘇州科技大學土木工程學院， 蘇州 215011 )

山區交通工程建設中往往形成隧道洞口仰坡，隧道開挖施工會造成仰坡土體產生巨大擾動，破壞邊坡土體原有的應力平衡狀態，導致坡體抗剪強度下降，極易誘發滑坡、崩塌等工程地質問題[1-4]。隧道洞口區域巖土體風化程度較大，風化裂隙發育且受地表水侵蝕嚴重，該區域的襯砌結構是失效破壞的多發地段，特別是當隧道洞口支護不及時或襯砌支護能力不足的情況下，容易發生襯砌變形破壞及支護拱脫離等現象。隧道洞口段穩定與邊坡工程密切相關[5-6]，仰坡穩定對隧道結構的安全起到至關重要的作用。地震誘發的邊坡滑動是主要地震地質災害類型之一[7]，其對邊坡穩定性的影響機制一直都是土力學研究的熱點和難點[8-11]。因此，如何分析地震力作用下隧道洞口仰坡穩定性是研究隧道工程建設及運營期安全性能的關鍵問題。

大量試驗研究表明，受開挖、天然沉積及后期加載等因素影響，巖土體黏聚力往往表現出顯著的非均質性和各向異性[12-15]，且邊坡表面分布著大量裂縫[16]。忽略巖土材料的各向異性和非均質性會導致邊坡穩定性分析產生誤差，從而影響含裂縫邊坡穩定性評價的準確性[17]。在中國邊坡工程相關設計規范的穩定性計算中多采用極限平衡理論，針對邊坡失穩的圓弧滑動面多采用圓弧滑動法、Bishop法及Morgenstern-Price 法，針對非圓弧滑面多采用不平衡推力法。然而，極限平衡法所得到的解既不是真實解的上限，也不是真實解的下限[18-19]。基于土體塑性力學理論，極限分析法首次由Drucker等[20]于1952年引入邊坡穩定性分析中，可得到邊坡穩定性分析的精確上下限解。Chen[18]最早將極限分析上限法應用于土體非均質性和各向異性下邊坡穩定性研究。之后，眾多學者考慮土體強度非均質性和各向異性影響，將極限分析上限法推廣至不同工況下邊坡的穩定性分析中[21-24]。Terzaghi[25]最早提出擬靜力法用于邊坡地震穩定性分析，本質上是由靜力穩定分析方法擴展而來，機理是將地震的瞬時作用等效為作用于潛在滑體上的水平和豎直方向的加速度作用。由于使用簡便，因而積累了大量的工程實際經驗，便于實際應用推廣。Chen等[26]在平動破壞機制和圓弧轉動破壞機制基礎上，提出一種更符合實際的對數螺旋破壞機制，得到地震力作用下非均質及各向異性邊坡穩定性臨界高度最優上限解。

已有地震力作用下考慮巖土體非均質及各向異性影響下的邊坡穩定性研究多關注于加筋土邊坡穩定性問題[27-28]，抗滑樁加固邊坡穩定性問題[29]，預應力錨索加固邊坡穩定性問題[30]，孔隙水壓力作用下邊坡穩定性問題[31]，而考慮土體強度非均質及各向異性影響下隧道洞口段仰坡地震穩定性研究相對較少。基于此，將土體黏聚力強度非均質和各向異性與極限分析上限理論相結合，同時引入土體強度折減理論，推導出水平和豎向地震力作用下隧道洞口段仰坡穩定性極限分析上限解計算公式，對比驗證所提計算方法應用的合理性，得到地震力作用下非均質及各向異性系數對隧道洞口仰坡臨界坡高、隧道拱頂破壞位置及仰坡安全系數的影響規律。以期為山區隧道洞口仰坡抗震穩定性設計提供理論參考。

1 極限分析上限法計算理論

1.1 計算模型

計算模型如圖1所示，依據相關聯流動法則，隧道洞口段仰坡滑體邊界為CD，滑體區域ABCD以角速度ω繞旋轉中心O作整體轉動破壞。隧道洞口段仰坡坡高為Hcr，坡面AB水平向傾角為β，仰坡滑移線起始點位置與坡肩距離為L，rh為潛在滑移面剪出口A′到圖1中滑體旋轉中心O的半徑，仰坡滑移線穿過隧道頂部位置與隧道洞口距離為Lt，α1為隧道洞口段仰坡高度相關系數、α2為隧道拱頂與潛在滑移面剪出口之間距離的相關系數。假定隧道洞口段仰坡為理想彈塑性模型，遵循Mohr-Coulomb強度準則，基于Chen等[18,26]提出的邊坡極限狀態下的對數螺旋轉動破壞機制，結合圖1可得仰坡潛在滑移面方程，可表示為

r=r0exp[(θ-θ0)tanφ]

(1)

式(1)中：r為對數螺旋線上任一點到圖1中滑體旋轉中心O的半徑；r0為對數螺旋線起點C到圖1中滑體旋轉中心O的半徑；θ、θ0分別為對數螺旋線上任一點與滑體旋轉中心O的連線與水平參考線的角度及對數螺旋線起點C與滑體旋轉中心O的連線水平參考線的角度；φ為土體內摩擦角。

由圖1可得到對數螺旋轉動破壞機制下的滑動面高度H、隧道洞口段仰坡高度Hcr、潛在滑移面分布L及隧道拱頂破壞位置Lt幾何關系無量綱表達式為

Hr=H/r0=exp[(θh-θ0)ψm]sinθh-sinθ0

(2)

H1r=Hcr/r0=sinθdexp[(θd-θ0)ψm]-sinθ0

(3)

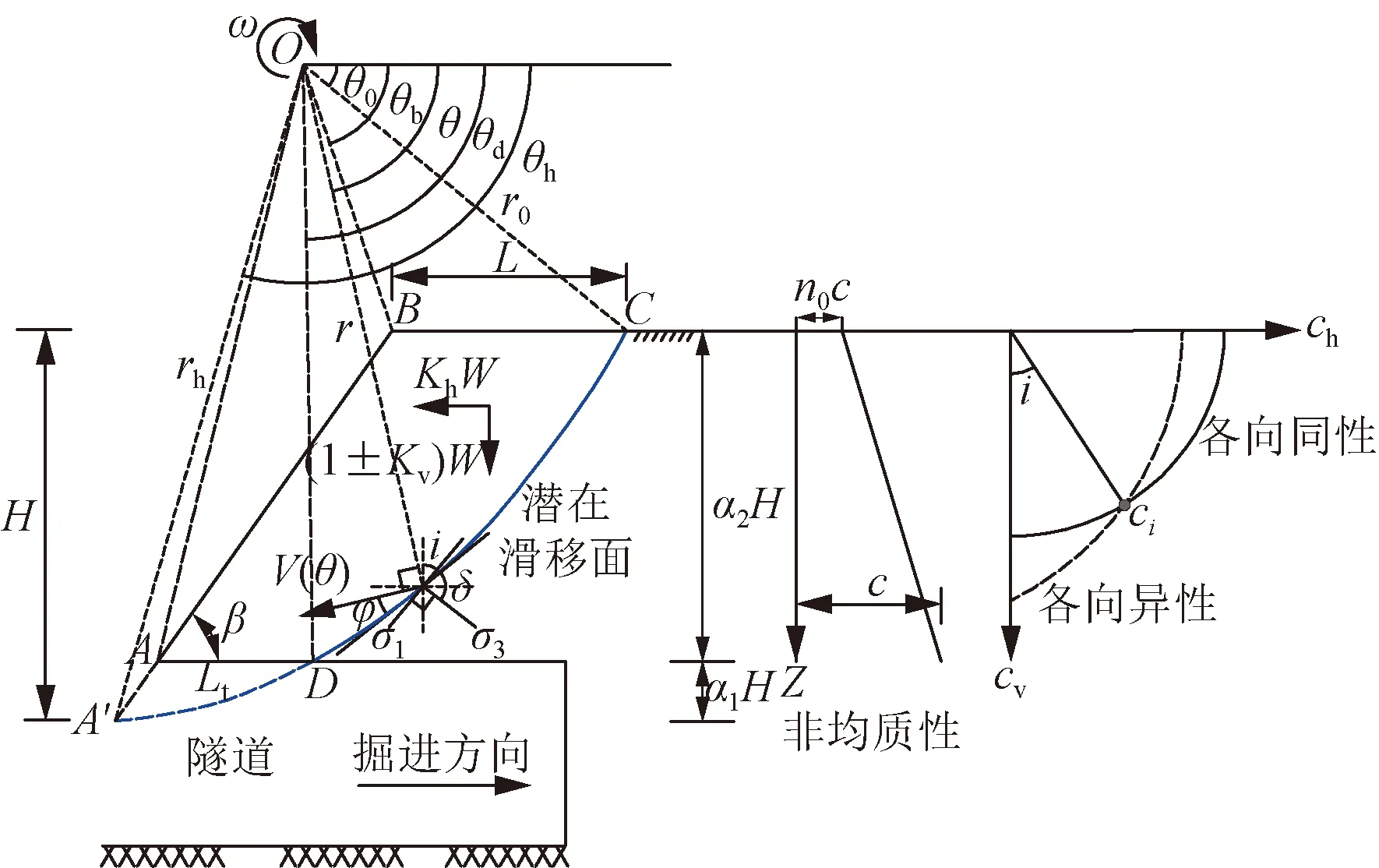
c為土體黏聚力；θd為潛在滑移面在隧道頂部剪出口D點與滑體旋轉中心O的連線與水平參考線的角度；n0為土體非均質系數；Kh為水平向地震力系數；Kv為豎直向地震動系數；W為土重；σ1、σ3分別為大主應力和小主應力；V(θ)為潛在滑移體運動速度；黏聚力ci與最大主應力方向一致，與豎直方向呈i角；δ為破壞面的切線與垂直于最大主應力線的夾角；ch和cv分別為土體水平向和豎直向黏聚力圖1 計算模型Fig.1 Model for calculation

Lr=L/r0

=sin(θ0+β)/sinβ-

sin(θh+β)exp[(θh-θ0)ψm]/sinβ

(4)

Ltr=Lt/r0

=cosθdexp[(θd-θ0)ψm]-

cosθ0+Lr+Hcrcotβ

(5)

式中：依據強度折減原理，ψm= tanφm= tanφ/Fs，其中Fs為土體強度折減系數；若穩定性計算中此折減系數增加值邊坡發生破壞時，此時的折減系數可稱為邊坡的安全系數，同樣可得到cm=c/Fs。

1.2 土體強度非均質及各向異性

考慮隧道洞口段仰坡土體黏聚力強度指標表現非均質和各向異性。土體強度各向異性表示土體的黏聚力隨方向發生改變的特性，圖1中黏聚力ci與最大主應力方向一致，與豎直方向呈i角，δ為破壞面的切線與垂直于最大主應力線的夾角，角度δ的值為π/4+φ/2[17,32]。進一步參考Lo[33]的研究成果，各向異性土體黏聚力計算表達式為

ci=ch+(cv-ch)cos2i

(6)

式(6)中：k=ch/cv為土體強度的各向異性系數。

土體強度非均質性表示土體黏聚力隨著深度的增加而線性遞增的特性，如圖1所示，假定土體非均勻性沿深度呈線性變化。當n0= 1.0時，土體強度表現為各向均質特性。土體同時受各向異性和非均勻性影響的黏聚力可表示為

[(1-n0)/Hr][sinθe(θ-θ0)tanφ-sinθ0]}

(7)

1.3 穩定性上限解

極限分析上限法認為對任一滿足運動許可的破壞機構，當令其外力功所做功率等于內能耗散率時，可得到極限破壞荷載的一個不安全上限，即所確定的極限狀態下的破壞荷載不小于真實極限荷載[18]，可表示為

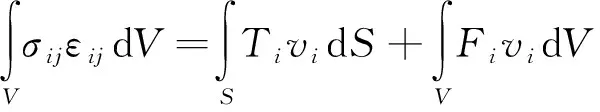
(8)

式(8)中：σij為通過相關聯流動法則與運動許可速度場中的應變率εij相關聯的應力場；vi為滿足幾何相容條件的速度場；Ti、Fi分別為機構邊界S上的面力和體積V中的體力。

基于極限分析上限理論，假設隧道洞口段仰坡失穩后以剛體形式運動，不考慮坡體內的局部破壞，當外力對潛在滑移體所作的功率大于坡體內部耗散功率時，仰坡將發生整體破壞。因此，在地震條件下，作用于潛在滑移體上的外力主要由滑體重力和地震力共同組成，坡體內部耗散功率主要是沿潛在滑移面的土體內能耗散功率。

1.3.1 潛在滑移體重力做功功率

滑動土體AEBCDA區域的外力功率為Wr，采用將A′EFA′區域土體重力做功功率減去A′AD區域土體重力做功功率及BFC區域土體重力做功功率。因此，AEBCDA區域的外力功率可表示為

(9)

式(9)中：γ為土體重度；f1～f4為與θ0、θd、θh、β、φ相關的函數，可分別表示為

(10)

1.3.2 地震力做功功率

隧道仰坡同時受水平向及豎直向地震力作用，依據極限分析上限理論，地震力對坡體所做功率為

(11)

式(11)中：Kh為水平向地震力系數；Kv為豎直向地震動系數；Wev、Weh分別為豎直向地震力做功功率、水平向地震力做功功率；f5～f8為與θ0、θd、θh、β、φ相關的函數，可分別表示為

(12)

1.3.3 潛在滑移面內能耗散率

潛在滑移面內能耗散率計算由圖1中對數螺旋間斷面CD的微分面積rdθ/cosφm與土體黏聚力ci及該間斷面上切向速度vcosφm相乘，總的內能耗散率為沿間斷面CD積分后計算可得

(13)

式(13)中：φm= arctan(tanφ/F)。

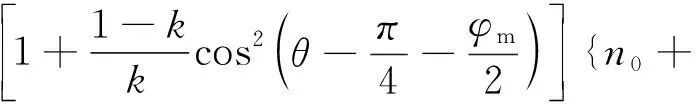
[(1-n0)/Hr][sinθe(θ-θ0)ψm-sinθ0]}

(14)

fd=fd1+fd2

(15)

式(15)中：fd和fd2可分別表示為

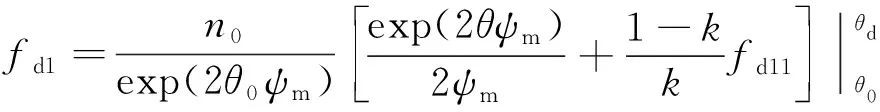
(16)

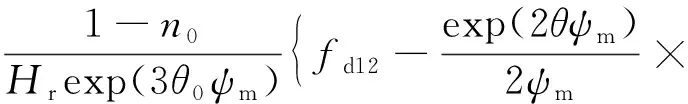
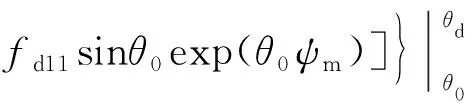
(17)

式(20)中：fd11、fd12及fd13可分別表示為

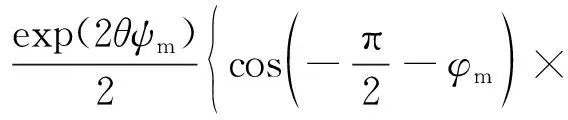
(18)

(19)

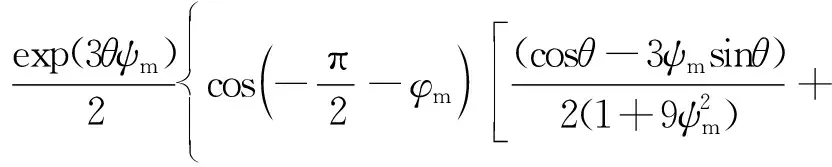
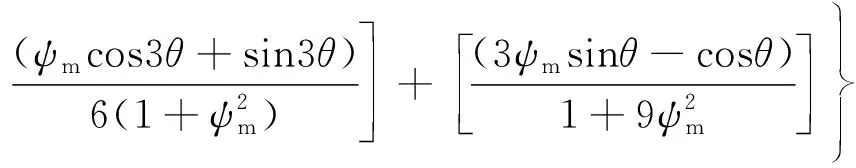
(20)

依據極限分析上限法原理，地震力作用下，考慮土體強度非均質及各向異性的隧道洞口段仰坡外力所做功率和內能耗散率應滿足以下平衡方程：

(21)

由式(21)可推導得到隧道洞口仰坡臨界高度Ns的表達式為

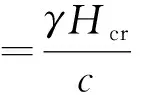
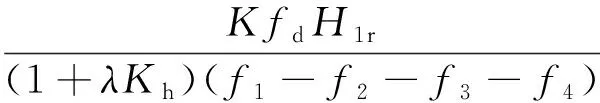
(22)

式(22)中：由臨界高度所確定的仰坡高度Hcr是仰坡在臨界狀態下(安全系數Fs= 1.0)所能達到的最大高度。

進一步變換式(22)，得到可用于求解仰坡安全系數Fs的隱函數表達式為

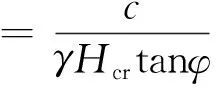
=[(1+λKh)(f1-f2-f3-f4)+

Kh(f5-f6-f7-f8)]/(KfdH1rψ)-1

(23)

對于滑面不確定的隧道洞口段仰坡，坡體內存在眾多潛在滑移面，其中得到最小仰坡臨界高度所對應的滑移面為最危險滑移面。仰坡臨界高度Ns及穩定性系數Nf可表示為參數θ0、θh、及θd的函數。基于MATLAB數值優化方法，便可確定相應于某一仰坡臨界高度的潛在最危險滑移面位置及隧道拱頂破壞位置，為使隧道洞口仰坡破壞機制滿足幾何條件，仰坡臨界高度最小上限解需滿足約束條件：

(24)

2 驗證分析

何毅等[34]利用極限分析上限法求解得到各向同性及均質條件下邊坡臨界坡高隨坡角變化規律，而土體各向異性系數n0= 1.0，非均質性系數k= 1.0可以認為是土體強度各向異性及非均質條件的特例。將本文方法退化為各向同性及均質條件與其穩定性解答對比，如圖2所示。可以看出，邊坡不同坡角β及內摩擦角φ影響下得到的邊坡臨界坡高Ns=γH/c解與文獻[34]結果非常接近。但當β= 40°、φ= 20°時，本文方法得到的臨界坡高略小于其解答，這是由于兩者優化方法存在差異。

為進一步驗證所提方法在地震力作用下的適用性，進一步將所得到的解答與Ling等[35]基于極限平衡法得到的不同地震力系數λ、Kh影響下的邊坡穩定性系數解c/γH進行對比，如表1所示，發現

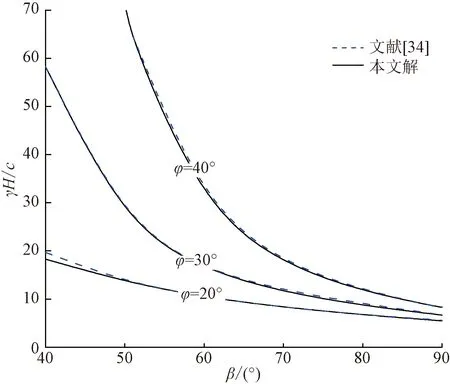
圖2 靜力條件下邊坡臨界坡高計算結果對比Fig.2 Comparisons of critical height influenced by static conditions

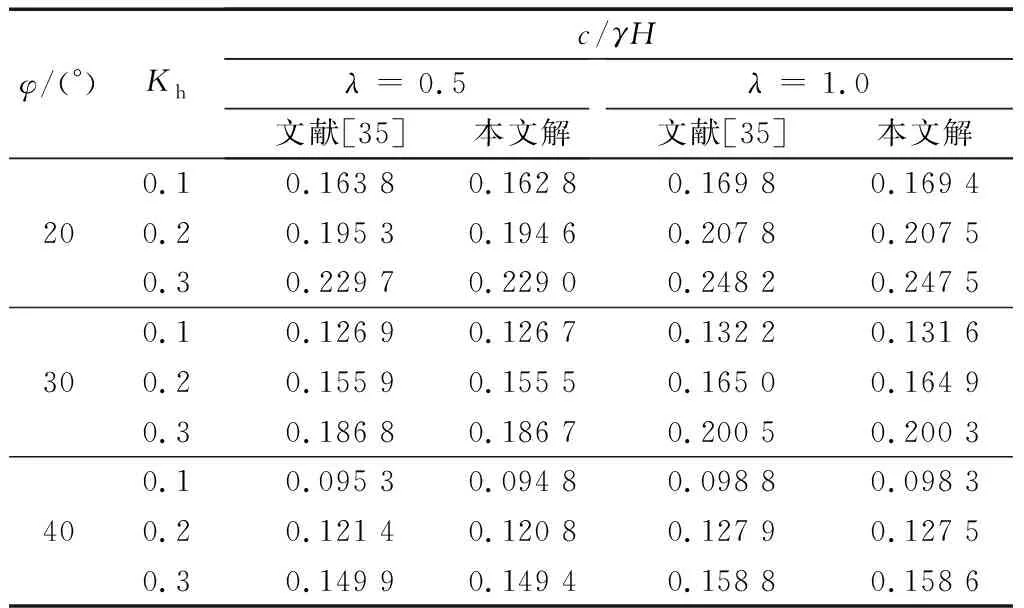
表1 地震力作用下邊坡穩定性系數計算結果對比Table 1 Comparisons of stability numbers influenced by seismic force

應用本文方法得到的解答與文獻[35]解答較吻合，且采用極限分析上限解普遍小于極限平衡解，說明極限分析上限解較極限平衡解更接近真解。因此，上述兩則算例的對比結果驗證了所提方法用于研究隧道洞口段仰坡穩定性的可行性。

3 計算結果分析

3.1 臨界坡高

穩定圖可用于判定已有坡體高度是否滿足邊坡穩定性要求。針對隧道洞口段仰坡，通過式(22)可得到邊坡臨界坡高γHcr/c，若巖土體重度γ及黏聚力ci已知，應用繪制的穩定圖即可得到保證隧道洞口段坡體穩定的臨界坡高。圖3、圖4給出土體各向異性、非均質性及地震力作用下的隧道洞口段仰坡臨界坡高變化規律。可以看出，非均質系數n0越大，γHcr/c越大，表明隧道洞口段仰坡的臨界坡高Hcr越大。而各向異性系數k越大，γHcr/c越小，表明維持隧道洞口段仰坡穩定所需的臨界坡高Hcr也越小。地震力對隧道洞口段仰坡臨界坡高影響明顯，表現為隨著水平地震力系數Kh的增大，γHcr/c減小，說明地震力越強時，仰坡為維持穩定所需的臨界坡高越小。此外，仰坡臨界坡高與隧道洞口段仰坡坡角β密切相關，如當坡角較小時，不同水平地震力系數Kh影響下的γHcr/c值差異顯著，而隨著坡角增大，這種差異逐漸減小。圖4中，λ為正值表明地震力作用與重力一致，即震動方向豎直向下，而λ為負值表明地震力作用與重力相反，即震動方向豎直向上，可以看出地震力豎直向上作用時的隧道洞口段仰坡臨界坡高明顯大于豎直向下的地震力作用時的臨界坡高。

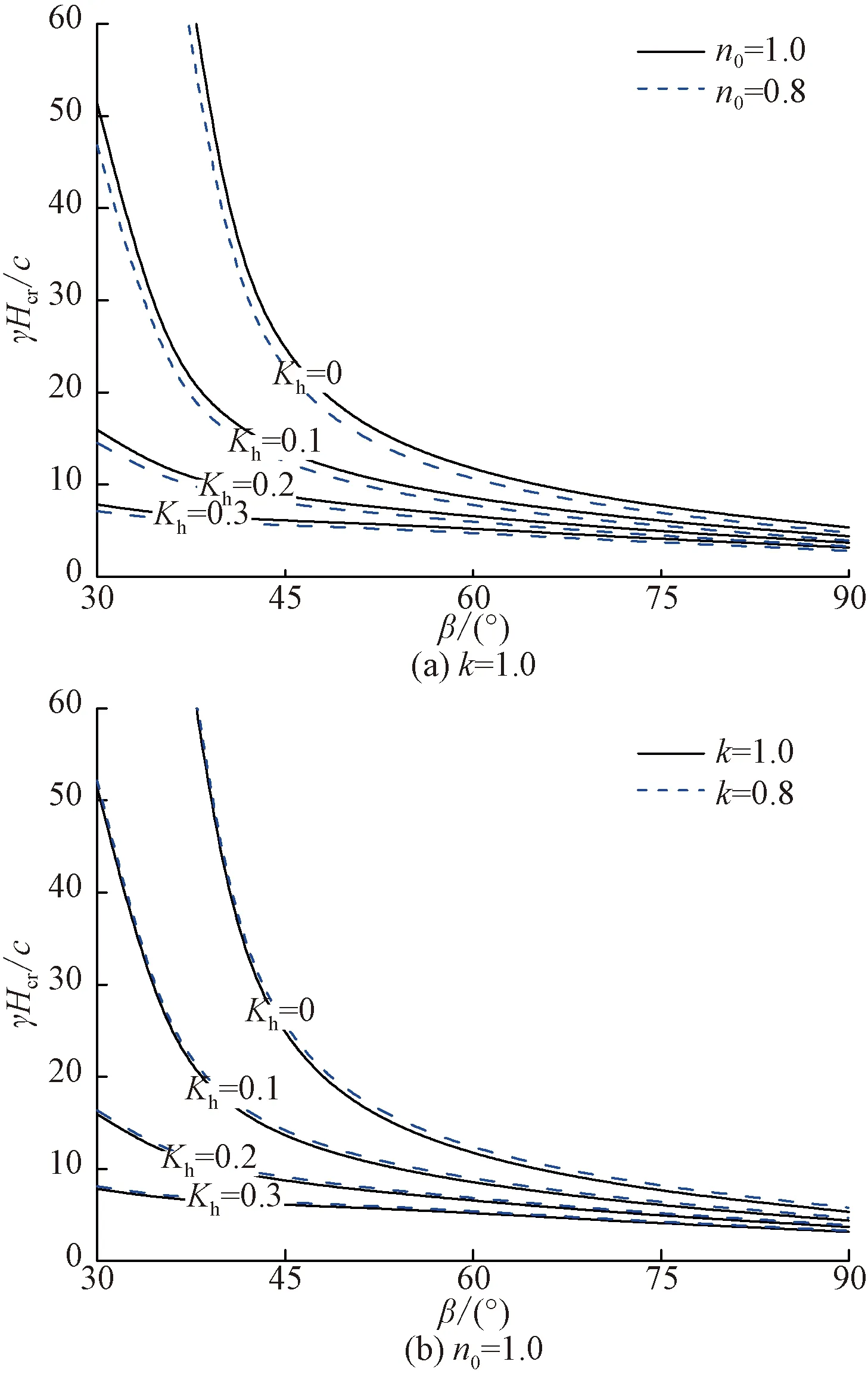
圖3 坡角及地震力對隧道洞口段仰坡臨界坡高影響規律Fig.3 Effect of slope angle and seismic force on critical height of slopes at tunnel entrance

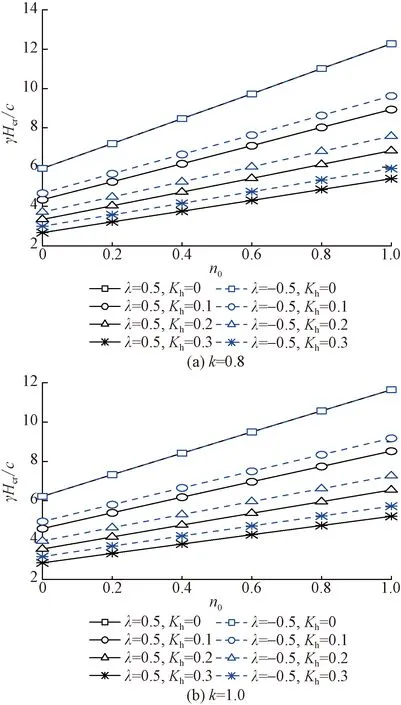
圖4 土體非均質及各向異性對臨界坡高影響規律Fig.4 Effect of soil inhomogeneity and anisotropy on critical height of slopes at tunnel entrance

3.2 隧道拱頂破壞位置

依據圖1建立的隧道洞口段仰坡破壞機制，潛在滑移面穿過隧道頂部，往往造成隧道拱頂發生破壞，因此，隧道拱頂破壞位置預測是進行隧道加固的重要環節。圖5～圖8給出土體各向異性、非均質性及地震力作用與潛在滑移面的初始位置L/Hcr及隧道拱頂破壞位置Lt/Hcr的關系曲線。可以看出，當土體各向異性系數n0及非均質性系數k增大時，潛在滑移面的初始位置L/Hcr及隧道拱頂破壞位置Lt/Hcr都呈增大的趨勢，但隨著k的增大，不同n0影響下的L/Hcr及Lt/Hcr差距逐漸縮小，直至k= 1.0時，數值基本趨于一致。同時，還可以明顯發現隧道洞口段仰坡潛在滑移面初始位置分布曲線與隧道拱頂破壞位置曲線規律保持一致，說明潛在滑移面位置與隧道拱頂失穩位置密切相關，這是由于坡頂滑移位置及隧道拱頂破壞位置分別對應潛在滑移面的起始及剪出位置。

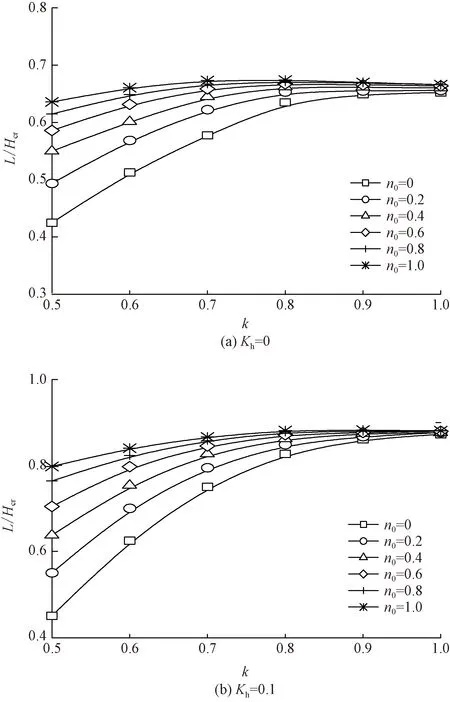
圖5 土體各向異性及非均質性對潛在滑移面 初始位置L/Hcr影響規律Fig.5 Effect of soil inhomogeneity and anisotropy on initial position of potential sliding surface L/Hcr

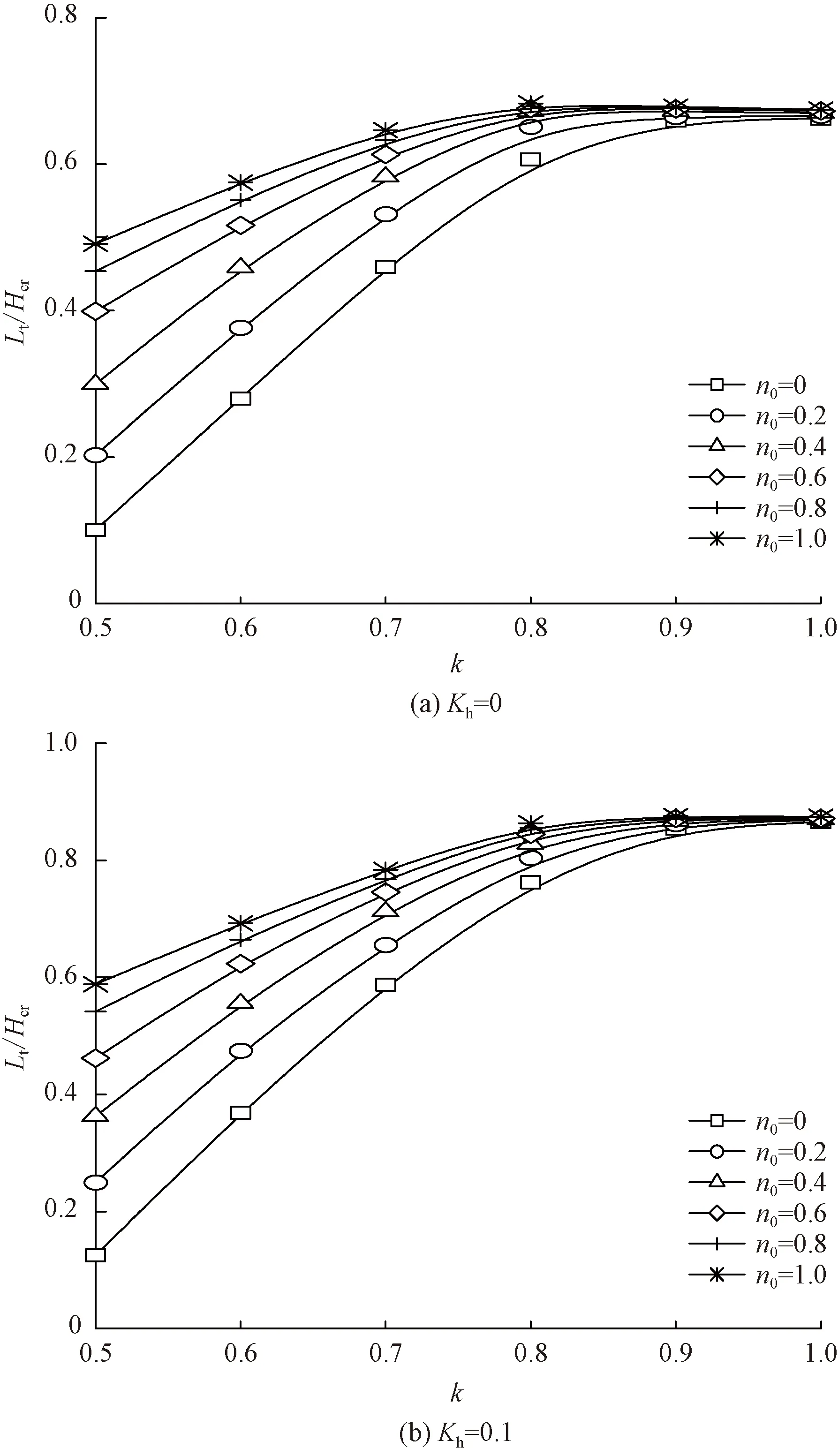
圖6 土體各向異性及非均質性對隧道拱頂破壞 位置Lt/Hcr影響規律Fig.6 Effect of soil inhomogeneity and anisotropy on failure location of tunnel vault Lt/Hcr

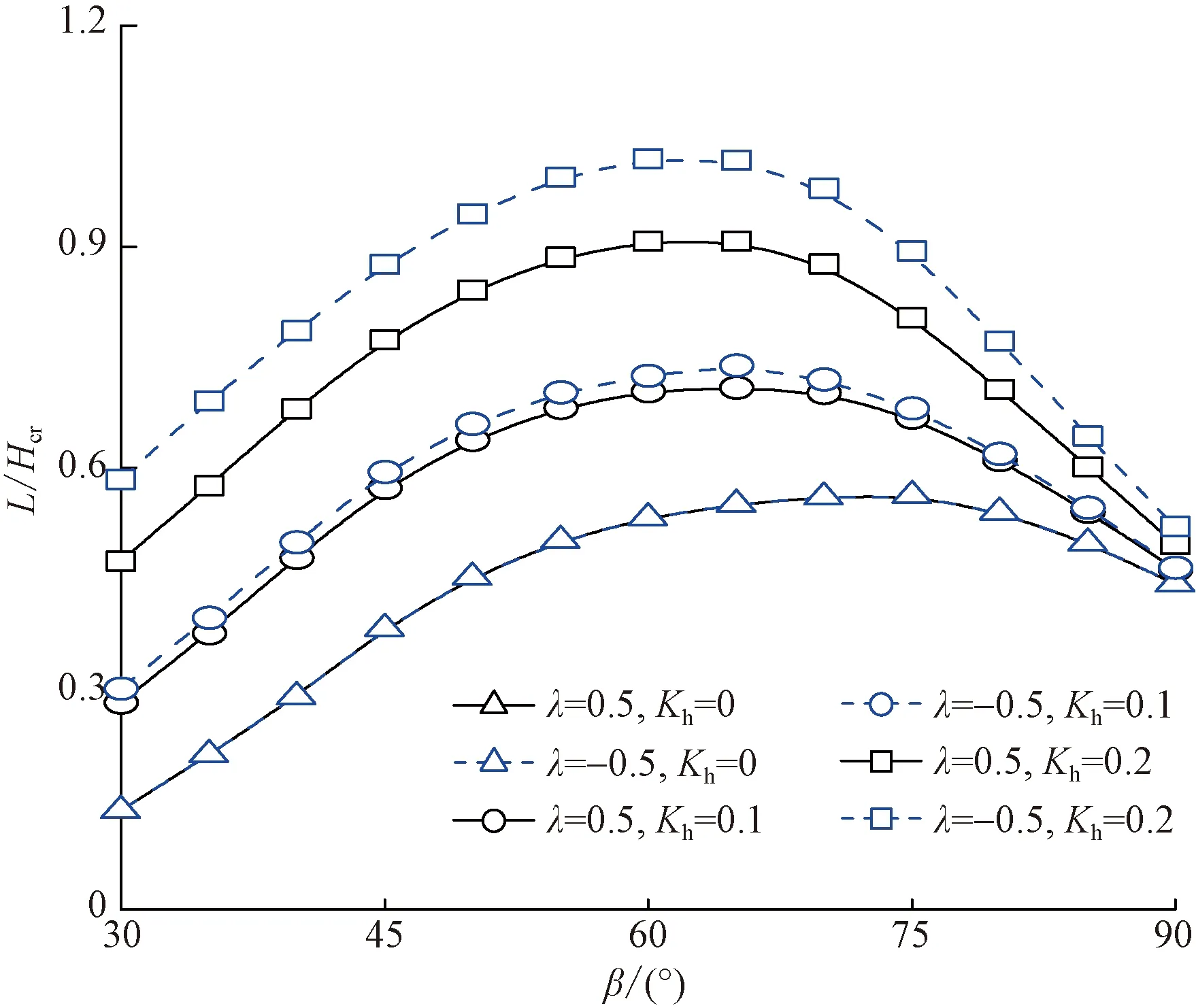
圖7 坡角及地震力對潛在滑移面初始 位置L/Hcr影響規律Fig.7 Effect of slope angle and seismic force on initial position of potential sliding surface L/Hcr

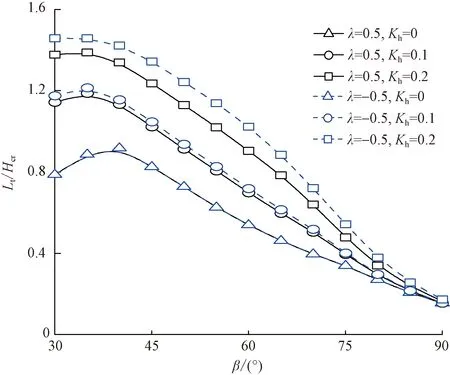
圖8 坡角及地震力對隧道拱頂破壞位置Lt/Hcr影響規律Fig.8 Effect of slope angle and seismic force on Lt/Hcr

從圖7、圖8中可以觀察到，水平向地震力系數Kh增大且豎直向地震力作用方向向上時，L/Hcr及Lt/Hcr皆增大，說明地震力作用將導致隧道洞口仰坡發生深層滑動，即初始滑移面遠離坡肩位置，隧道拱頂破壞范圍更廣。坡角β對L/Hcr及Lt/Hcr影響較大，表現為隨著坡角β的增大，坡頂初始滑移位置呈先增大后減小的趨勢，在β= 60° ～ 70°時，L/Hcr達到最大值，即坡頂初始滑移位置離坡肩最遠。當坡角小于40°時，Lt/Hcr呈遞增趨勢，超過此角度，隨著坡角的增大，Lt/Hcr呈遞增趨勢，即仰坡潛在滑移面穿過隧道拱頂的位置距離隧道洞口較近。

3.3 仰坡安全系數

安全系數作為評價邊坡穩定性的重要指標，已在工程實踐中得到普遍應用。然而，極限分析上限法無法直接求得邊坡安全系數，基于此，結合強度折減理論及含安全系數Fs的隱函數方程式[式(15)]，通過繪制一種橫坐標tanφ/Fs、縱坐標c/γHcrtanφ的穩定圖間接計算隧道洞口段仰坡安全系數。計算實現過程如下：算例中設定隧道洞口段仰坡坡角β= 60°，各向異性系數n0= 0、0.2、0.4、0.6、0.8、1.0，非均質系數k= 0.5、0.6、0.7、0.8、0.9、1.0，λ= 0.5，Kh= 0.1。

圖9 給出各向異性系數n0、非均質系數k影響下隧道洞口仰坡穩定圖。可以看出，穩定圖呈顯著的非線性分布特征，非均質系數k影響下的穩定圖曲線差異較小，各向異性系數n0的變化對穩定圖曲線分布影響較明顯。給定仰坡坡高Hcr=10.0 m，土體參數c= 40 kPa，φ= 20°，γ= 18 kN/m2，當k= 1.0,n0= 1.0;k= 0.6,n0= 1.0;k= 1.0,n0= 0.8時，可得到縱坐標c/γHcrtanφ= 0.611，進一步找到圖9中該縱坐標值對應的橫坐標tanφ/Fs值，分別為tanφ/Fs= 0.357、0.308、0.379，將φ= 20°代入可反算得到安全系數分別為Fs= 1.02、1.18、0.96。

針對土體強度各向異性及非均質性的不同分布情況，研究n0及k值變化對隧道洞口仰坡安全系數的影響規律，如圖10所示。可以看出，在地震力作用下，隨著各向異性系數n0的增大，仰坡安全系數Fs呈遞增趨勢，而非均質系數k越大，仰坡安全系數Fs越小。

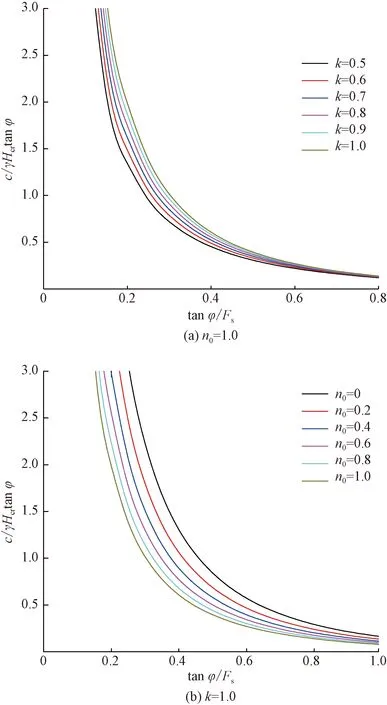
圖9 土體非均質及各向異性影響下仰坡穩定圖Fig.9 Stability charts of slopes at tunnel entrance considering soil inhomogeneity and anisotropy

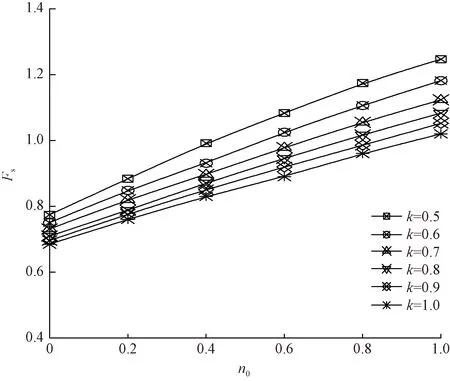
圖10 隧道洞口仰坡安全系數與土體非均質及 各向異性關系Fig.10 Relationship between safety factors of slopes at tunnel entrance and soil inhomogeneity and anisotropy

4 結論

應用極限分析上限法結合土體強度折減理論，構建了考慮土體強度非均質及各向異性的隧道洞口仰坡地震穩定性分析模型，推導出穩定性極限分析計算公式，得到仰坡臨界坡高、隧道拱頂破壞位置的最優上限解及相應的穩定圖，并建立一種以穩定圖計算仰坡安全系數的方法。得出如下主要結論。

(1) 非均質系數n0越大，隧道洞口段仰坡的臨界坡高Hcr越大，而各向異性系數k越大，維持隧道洞口段仰坡穩定所需的臨界坡高Hcr也越小；坡角較小時，不同水平地震力系數Kh影響下的臨界坡高差異顯著，而隨著坡角增大，差異逐漸減小。

(2) 土體強度各向異性系數n0及非均質性系數k增大時，潛在滑移面的初始位置L/Hcr及隧道拱頂破壞位置Lt/Hcr皆增大，表明初始滑移面遠離坡肩位置，隧道拱頂破壞范圍更廣。

(3) 通過引入算例繪制穩定圖提出間接計算隧道洞口段仰坡安全系數的方法，發現在地震力作用下，隨著各向異性系數n0的增大，仰坡安全系數Fs呈遞增規律，而非均質系數k越大，仰坡安全系數Fs越小。