數形結合，讓體驗充盈課堂

喻菊

一、教學分析

（一）內容與學情的契合

“數與形”是人教版小學數學六年級上冊數學廣角的知識內容。兒童思維以具體形象思維為主，數形結合思想在小學階段得到廣泛應用，它使很多抽象的數學問題直觀化、生動化，將抽象思維以形象思維的方式呈現與應用，提高了學生學習的興趣，也有助于學生把握數學問題的本質。

六年級學生對數形結合其實并不陌生，數形結合思想一直伴隨著他們的數學學習，并已經積累了一定的活動經驗。本節課的學習不在于掌握某個具體知識內容，而是要進一步滲透數形結合思想，理解數形結合的本質，掌握數形結合的方法，有意識地運用數形結合的方法解決問題，逐步發展學生抽象思維，提升學生數學素養。教師要從數學思想的角度把握教材內容的本質，更加深入地解讀教材，從關注技能轉向關注能力。

（二）教學目標

1.讓學生經歷觀察、猜想、驗證、歸納等活動，以形助數，以數輔形，發現規律，培養學生數形結合的意識。

2.通過動手擺小方塊表示數，感悟以形助數、以數輔形的重要性，積累數形結合解決問題的活動經驗。

3.體驗數形結合數學思想方法的價值，感受數學的魅力。

（三）教學重點與難點

由“數”思“形”，由“形”表“數”，借助數形結合思想方法，多角度地解決數學問題，深化數學思維。

二、教學過程

（一）計算挑戰——引出課題

師：聽說咱們班同學的計算能力都不錯，敢接受我的挑戰嗎？

（課件依次出示：1+3、1+3+5、1+3+5+7、1+3+5+7+9+11+13+15+17，學生計算的速度由快到慢，答案也由確定慢慢地不確定起來。在計算最后一道題時，學生給出的答案有的是49，有的是81。計算方法有的是不斷連加，有的是湊整）

師：老師這里還有一個好方法，只要看一眼這個算式，就能立馬知道答案，你們相信嗎？

師：我們先來觀察這類題有怎樣的共同特點？

生：都是連續的奇數。

師：而且都是從幾開始的？

生：1。

（教師板書：從1開始的連續奇數的和）

師：誰來給老師出題？有計算器的同學負責驗證，看看老師是否算對了？

生：1+3+5+7+9+11+13+15+17+……+99=？

（教師快速報出結果2500，學生驗證無誤）

師：對于剛剛這樣的計算，老師這樣的速度，你們有什么想說的嗎？

生：太快了！

師：其實，老師剛剛看到這些算式、這些數時，腦中想到的是一些圖形。將數和形相結合，就能很快地幫助我們找到答案。你們肯定很好奇，老師腦中想的是一個什么樣的圖形呢？這就是我們今天要研究的內容。（板書：數與形）

【思考】在“計算挑戰”中，問題從易到難，學生解答問題由快到慢。當已有的知識技能不能更好、更快地解決問題時，教師的“表演秀”就輕松地調動了學生的學習欲望，這時再介紹解決問題的新途徑——數形結合，激發了學生學習的興趣。

（二）活動操作——發現規律

師：我們就從簡單的1開始。看到1，你們能想到什么圖形？

生：1個長方形、1個正方形……

師：我們用1個正方形來表示1。

1.活動探究：1+3

活動要求：利用小正方形拼成一個大一點的圖形來表示這個算式，并且有利于算出總數。先獨立思考，再把自己的想法和同桌進行交流。

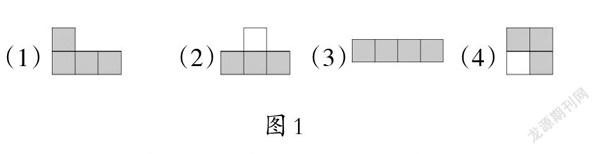
學生取出學具袋，可以把小正方形貼在黑色卡紙上，學生獨立操作，教師巡視并找出具有代表性的作品進行交流評價（如圖1）。

大多數學生認為第（4）個圖形不僅可以直觀地表示出算式，而且有利于計算出正方形的個數。

師：現在1+3可以怎么算？

生：2的平方。

師：很有意思。原來我們看這樣的一個算式就只是一個算式，看這樣的一個圖形就只是一個圖形，這節課我們用不同的眼光，發現算式借助圖形的表達找到了新的計算方法，這就是數形結合思想。

2.活動探究：1+3+5

活動要求：利用手中的小正方形再拼搭成一個大一點的圖形來表示這個算式，并列出算式計算出結果。

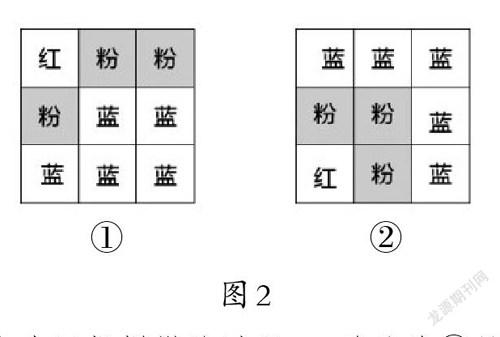
學生再次拼搭，教師選擇兩組具有代表性的作品進行交流（如圖2）。

學生先匯報拼搭的過程，一致認為②號圖形的拼搭很有規律。②號圖形按“┐”形拼搭逐漸變成更大的正方形。

師：現在看著這個大一點的正方形，你們能列一個加法算式嗎？

生：1+3+5。

師：它的結果可以怎么計算？

生：3的平方。

師：剛剛是2乘2，現在是3乘3，2和3是怎么確定的？

生：小一點的正方形邊長是由2個小正方形邊長組成的，所以邊長是2;大一點的正方形邊長是由3個小正方形邊長組成的，所以邊長是3。

生：原來是2個加數，所以它的邊長是2;現在有3個加數，所以它的邊長是3，就（比原來）增加了一層。

師：順著思路繼續想，我想在此基礎上拼搭一個更大一點的正方形，需要增加幾個這樣的小正方形？

生：7個。

師：增加在哪里？比畫一下。

（學生書寫“┐”）

師：看到這樣的一個圖形，可以幫我們解決一個怎樣的加法問題？

生：1+3+5+7。

師：它的結果怎么算呢？

生：看作4乘4等于16。

師：4是什么意思？

生：4是加數的個數。

生：4是正方形的邊長。

師：我們從數的角度來看1+3+5+7=16，4×4=16，所以1+3+5+7=4×4。從形的角度來看，也可以發現1+3+5+7=4×4。

3.鞏固提升：1+3+5+7+9

師：不拼搭，你腦中能想象出一幅圖嗎？是一幅怎樣的圖？

生：能想象出一個5乘5的正方形。

師：算式的結果可以怎樣算？

生：5乘5，5的平方是25。

師：通過剛才的探究，你們找到解決這類算式的辦法了嗎？

生：從1開始連續奇數的和等于這些奇數個數的平方。

（師生進行舉例驗證）

師：“1”能寫成這樣的算式嗎？（板書：1=12）

師：他們的總結，給我們找到了解決這一類問題的訣竅：從1開始的連續奇數的和等于這些奇數個數的平方。

【思考】人教版小學數學六年級上冊“數學廣角——數與形”中的例題編排是先呈現一組“形”，再輔以“數”來發現圖形變化中蘊含的規律，從而達到數形結合的點睛之處。在教學這節課時我們反其道而行之，先有數，從“數”到“形”，借“形”表“數”，通過思考“怎么擺算得結果最快？”引導學生對“形”進行優化，發現“形”的規律，即幾個連續奇數的和用小方塊按“┐”形逐層擺放可以拼搭成一個大正方形，不僅能清楚地表達數，而且計算總數也很方便。發現“數”的規律，原來求幾個連續奇數的和除了可以用加法計算，還可以用奇數個數的平方進行計算。在這個學習過程中，學生在不知不覺中就借助“形”來思考“數”的問題，而“數”的問題在“形”的輔助下又產生了新的解決方法。

（三）實踐嘗試——問題解決

1.1+3+5+7+9+11+13+15+17=？

師：回到口算挑戰的最后一題，你們腦中有圖嗎？它是一個什么樣的圖？

生：是邊長為9的正方形。

師：可以快速地算出總數嗎？是多少？

生：9×9=81。

師：和之前“湊整法”比較，你們覺得有什么想說的？

生：更簡單了。

2.1+3+5+7+5+3+1=？

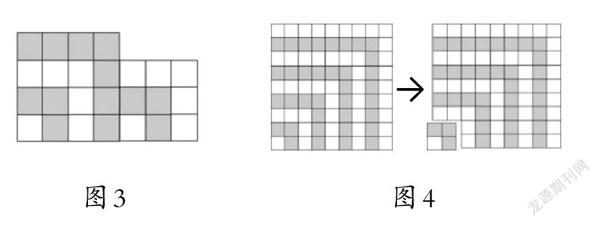
學生思考發現，可以將算式分成1+3+5+7和5+3+1兩部分，想象出圖3，再運用結論進行計算。

師：規律總結出來，還可以這樣靈活著用。

3.5+7+9+11+13+15+17=？

學生把算式看成1+3+5+7+9+11+13+15+17-（1+3），抽象出圖4，即從邊長為9的正方形中減去一個邊長為2的正方形。

師：太了不起了，在短時間內腦海中有了這么多的圖形幫助我們解決數的問題。

4.2+4+6+8+10+12+14=？

師：一開始我們研究的是連續奇數的和，現在應該怎么思考？

生：我們可以將算式中的每個數減掉1，他們又回到了1+3++5+7+9+11+13，然后先算出7的平方，再加7，結果等于56。

師：還有沒有別的方法？

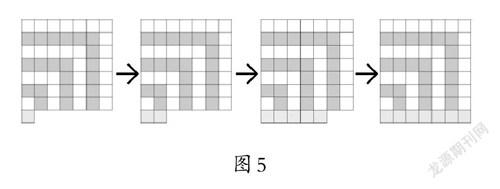
課件逐步演示正方形演變成長方形的過程（如圖5）。

師：7個1就全部補在哪里？

生：正方形的下面。

師：現在你們看到的是一個什么圖形？

生：拼成了一個長為7、寬為8的長方形。

師：可以快速地算出它們的和是多少嗎？

生：長方形中有56個小正方形，所以和是56。

師：真好，我們從連續奇數的探究到連續偶數的探究都給解決了，了不起。

5.1+3+5+7+9+11+13+15+17+……+51=？

師：有人覺得難了，它難在哪兒啊？

生：個數沒法確定。

師：咱們碰到難題時要知難而進。

師：知難而進，進的確是一種勇氣。有的時候知難而退更是一種智慧，但是這個退不是不做，退一退，是從簡單入手，找到它的突破口。

學生結合課件觀察算式1+3+5+7+9+11中加數的個數6與奇數11之間的關系，最終發現：（最外圈數+1）÷2=正方形邊長（如圖6所示）。

師：現在咱們找到了解決問題的關鍵步驟了。算式的個數怎么確定？

生：51加1再除以2，得26。

師：1+3+5+7+9+11+13+15+17+……+51=262。

【思考】本節課的練習中既有基礎訓練，又有變式訓練。教學中，教師有意識地追問學生“腦中有圖嗎？”“腦中有什么樣的圖？”，學生腦海中的圖形也漸漸地隨著數的變化而發生變化。由1個正方形，到出現2個組合的正方形，再到有空缺的正方形;又從正方形到長方形，從“形”中覓“個數”……學生在這樣的練習中，將數與形緊密地結合在一起，有數就有形，形中能見數，同時練習的精巧設計打破了學生對數與形的認知局限，數變形亦變，數形結合思想在學生的腦海中生根發芽，學生對原有的概念認知賦予新的理解。

（四）拓展延伸——溝通聯系

1.在以往的學習中，大家有沒有數形結合的經驗？（播放微視頻）

2.圖形判斷（如圖7）。學生發現圖形的表達要借助數據才更加精準，從而感悟數學數形結合的魅力。

師：難怪數學家華羅庚爺爺這樣說：數缺形時少直觀，形少數時難入微，數形結合百般好，隔離分家萬事休。

【思考】本課的最后，教師通過舉例說明數形結合無處不在。在小學階段的數學學習中，我們可以借助圖形來認識自然數、小數和分數，在圖形的幫助下學習加、減、乘、除四則運算，在一些圖形面積公式的推導過程中，數與形也是緊密相連的。在位置與方向的學習中，數形結合能準確定位，枯燥的數據用統計圖表直觀地表示出來，方便進行數據分析和決策。離開課本，大自然里也有神奇的數與形。從含苞待放的花朵到玫瑰花瓣，再到植物的種子，數都無處不在。最后借助華羅庚的詩詞讓學生品味數形結合思想，讓學生的數學學習變得更加有意思。

（作者單位：江西省南昌市灣里管理局教科體局教研室）

投稿郵箱：405956706@qq.com