基于故障鏈聚類算法的電網關鍵線路辨識

黎壽濤， 夏成軍, 鐘明明， 管霖

(1. 華南理工大學電力學院，廣東 廣州 510640；2. 廣東省新能源電力系統智能運行與控制企業重點實驗室，廣東 廣州 510663)

0 引言

近年來，國內外發生了多起由連鎖故障引發的大停電事故[1—3]，造成了巨大的經濟損失與惡劣的社會影響。研究表明，在連鎖故障的發展過程中極少數線路有至關重要的作用[4]，高效且準確地識別出這些關鍵線路，對于揭示電網薄弱環節、提高電力系統可靠性具有重要的意義。

基于復雜網絡理論的關鍵線路辨識算法首先將電力系統簡化為抽象模型，再依據節點介數[5]、線路效能權值[6]、潮流熵[7]等拓撲特征對線路進行重要性排序。此外，亦有學者建立了如ORNL-PSERC-Alaska(OPA)模型[8]、Manchester模型[9]、基于直流潮流法的電力系統解列模擬器(direct current power flow simulator of power system separation，DCSS)模型[10]等連鎖故障仿真模型，試圖刻畫電力系統連鎖故障的演化過程，并從中找出對故障發展具有推波助瀾作用的關鍵線路。

上述仿真模型或電力系統實際運行所產生的故障鏈數據蘊含了豐富的連鎖故障信息，通過分析不同故障鏈間的共同特征及發展規律，同樣能實現關鍵線路的辨識。文獻[11]利用Apriori算法對交直流連鎖故障鏈進行頻繁項挖掘，有效地識別出危及系統安全的強關聯規則；文獻[12]通過FP-growth算法對故障鏈集合進行數據挖掘，辨識出了不同故障發展過程中的危險線路；文獻[13]根據故障鏈集合構建了連鎖故障時空圖，并從觸發與擴大連鎖故障2個角度出發，分類辨識出了系統中的脆弱線路。然而，故障鏈集合中的數據可能由不同的連鎖故障演化模式產生，各模式下起主導作用的關鍵線路亦不盡相同[13]。若在進行關鍵線路辨識前，預先對故障鏈序列的相似性進行度量，根據序列間相似的演化規律或關聯特征進行聚類，并對相似度較高的故障鏈集合進行分類評估，可進一步提高關鍵線路辨識精度與效率[14]。

文中首先根據熱量累積效應構建了改進DCSS連鎖故障仿真模型，并與隨機化學(random che-mis-try，RC)法相互配合，高效生成了含豐富時序信息的故障鏈集合。在此基礎上，文中引入編輯距離(edit distance,ED)衡量故障鏈間的相似程度，并通過凝聚式層次聚類算法實現了故障鏈集合聚類。將完成聚類后的故障鏈集合分別進行線路風險重要度排序，名次靠前的線路即為相應連鎖故障演化模式中起主導作用的關鍵線路。以Matpower 2 383節點系統為例，對不同算法所辨識的關鍵線路進行容量擴建，并根據擴容后系統連鎖故障風險水平的下降量化比較了所辨識線路的重要程度，對比結果進一步證明了文中所提模型及算法的有效性。

1 連鎖故障仿真模型

1.1 故障鏈集合生成

DCSS[10]是一種基于直流潮流法建立的連鎖故障仿真模型，主要面向過載主導型連鎖故障，考慮在無功較為充足的純交流系統中因線路過載而發生相繼失效的連鎖故障過程，其仿真速度快且沒有收斂性問題。DCSS模型通過對線路過載功率進行時間積分，模擬反時限保護機制，但當重載線路處于臨界狀態時，累計積分值可能被多次清零，所求線路跳閘的用時變長，使得模型所描述的故障時序特性可能與實際情況存在較大出入。因此，文中根據熱量累積效應[15]建立更合理的改進DCSS連鎖故障仿真模型。

首先，假設線路L的潮流PL超過限值Pmax,L，根據線路流過潮流對導線的熱效應，可近似計算出線路L在t時刻的瞬時溫度TL(t)。

(1)

式中：TL(t)為線路的瞬時溫度；PL為線路L流過的功率；Te(PL)為線路流過該功率時的平衡溫度；ν，α為線路熱效應的相關參數，皆取決于線路本身；Tenv為環境溫度；TL(0)為初始溫度。

將線路過熱保護的溫度觸發閾值Tmax,L代入式(1)，可算得線路L的過熱保護動作時間Δttrip,L。

(2)

在給定電網參數的前提下，通過式(2)可快速計算出下一次故障跳閘線路及相應動作時刻。

上述所建立的改進DCSS模型能高效且準確地生成故障鏈集合，具體流程見圖1，具體步驟為：

(1) 載入電網模型，初始化電網的運行狀態。

(2) 設置初始故障，將相應故障線路作為初始擾動進行開斷，第j條故障鏈Cj的初始故障線路集合為Linit,j。

(3) 通過孤島判定程序對線路開斷后的電網進行孤島判定。假如有新的孤島生成則進行發電機有功出力調整，如不能在規定時間內實現負荷與出力之間的平衡，則進行切機切負荷操作；假如沒有新的孤島出現，則直接轉至步驟(4)。

圖1 故障鏈集合生成流程Fig.1 Flow chart of fault chain set generation

(4) 對每一個仍處于運行狀態的孤島執行直流潮流運算。

(5) 依據步驟(4)所算得的潮流結果判斷是否有線路過載，如果仍有過載線路，則轉至步驟(6)，否則轉至步驟(7)。

(6) 將過載線路的潮流PL代入式(2)，計算下一次線路動作時間Δttrip,L，相應開斷線路記為Lnext，總仿真時間跳轉至tnext。記錄跳閘線路與相應的動作時刻{Lnext,tnext}后跳轉至步驟(3)。

(7) 連鎖故障仿真過程結束，根據步驟(6)所記錄的所有線路開斷信息{Lnext,tnext}及最終負荷損失Ploss生成故障鏈Cj。

(8) 重新選取初始故障線路形成初始故障集Linit,j，并重復步驟(2)～(7)生成故障鏈Cj，直至故障鏈樣本足夠多或滿足仿真退出條件。

對于較小的系統，或對計算速度無較高要求的搜索過程，初始故障集Linit,j可設定為系統中所有線路組合，通過遍歷法來進行連鎖故障分析，但當電網規模較大時，組合規模及計算量急劇增加，將面臨“維數災”的挑戰。為兼顧搜索時間與搜索精度，文中采用效率較高的RC法[16]來提高故障鏈的生成效率。RC法屬于無偏抽樣，即所得的初始故障集不依賴于任何先驗的概率或者指標，生成的故障鏈集合樣本較為全面地涵蓋了多種故障演化路徑，為后續的聚類分析及數據挖掘提供了更加豐富的數據樣本。

如圖2所示，某些連鎖故障仿真模型按故障演化階段進行線路開斷。以OPA快動態過程模型[8]生成的故障鏈如圖2(a)所示，其同一階段中多條線路開斷，不區分先后順序，此類故障鏈易造成無效規則的誤篩，增大后續數據挖掘難度。相比之下，如圖2(b)所示的通過改進DCSS模型仿真生成的故障鏈物理含義明確，包含更豐富的時序信息，既有線路開斷的先后順序，又記錄了相應的開斷時刻，能較真實地刻畫連鎖故障的演化過程，為后續分析提供更合理的樣本依據。

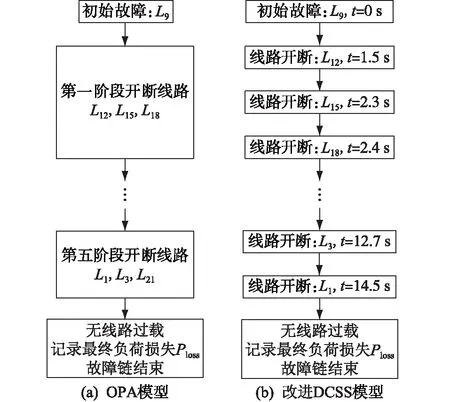
圖2 2類連鎖故障仿真模型所生成故障鏈的對比Fig.2 Comparison of fault chains generated by two kinds of cascading failure models

1.2 故障鏈的風險評估

文中采用文獻[17]中的概率風險法進行故障鏈的風險評估，定義故障鏈Cj造成的后果與發生概率分別為E(Cj)，p(Cj)。

1.2.1 連鎖故障后果

連鎖故障后果通常以系統負荷總損失、電網解列程度、故障鏈長度(停電線路數)等指標來衡量。負荷損失是連鎖故障在電力系統中造成的最直接后果，因此文中采用系統負荷總損失來衡量連鎖故障的后果。

E(Cj)=Ploss,j

(3)

式中：Ploss,j為第j條故障鏈Cj最終所造成的系統負荷總損失。

1.2.2 連鎖故障概率

根據1.1節中的定義可知，改進DCSS模型對于任意給定的N-k初始故障能且僅能生成唯一的故障鏈Cj及相應的負荷損失Ploss,j，即連鎖故障的發生概率由N-k初始故障所決定，文中定義故障鏈概率p(Cj)為：

(4)

式中：k為初始故障元件數；Linit,i為初始故障集Linit,j中的第i線路；U(Linit,i)為線路Linit,i的不可用率，可通過式(5)求得。

U(Linit,i)=λtDur/8 760

(5)

式中：λ為線路的平均失效頻率；tDur為平均修復時間。獨立事件的不可用率乘積表示多條線路同時失效的概率，即為以N-k故障為初始故障的連鎖故障發生概率。

將上述的故障鏈后果和故障鏈概率相乘，則可計算出事故鏈的負荷損失期望值R(Cj)，用于表征事故鏈的風險。

R(Cj)=E(Cj)p(Cj)

(6)

故障鏈集合S的連鎖故障風險等于所含全部故障鏈的風險之和。

(7)

2 基于ED的故障鏈層次聚類

2.1 ED的定義

在時間序列數據挖掘的諸多任務和問題中，序列相似性度量是最基礎的問題。以動態時間歸整(dynamic time warping，DTW)算法為代表的時間序列度量方法已廣泛應用在電力系統中，其通過對電流、電壓等時間序列的波形輪廓進行匹配，完成故障源辨識[18]、擾動分類[19]等任務。而改進DCSS模型所生成的故障鏈本質是事件序列，如圖2(b)所示，此類序列具有不等長、離散性等特點，因此文中引入更直觀的ED算法，計算故障鏈事件序列間的相似程度，為后續的分類過程提供聚類依據。

ED[20]是指將某一序列Cx通過插入、刪除與替換3種編輯操作轉換至另一序列Cy所需要的最小操作步數。假設存在2條由改進DCSS模型生成的故障鏈Cx，Cy，按線路先后開斷的次序可表示為：

(8)

式中：Lx,1為故障鏈序列Cx中第1條開斷的線路；m為Cx中開斷線路的總數(Cy同理)。Cx與Cy之間的ED可通過構造一個(m+1)×(n+1)維矩陣D遞歸求取，矩陣元素di,j的計算公式為：

di,j=min(di-1,j+1,di,j-1+1,
di-1,j-1+Lx,i⊕Ly,j)

(9)

特別地，當i=0或j=0時，di,j= max(i,j)。其中，?表示異或運算，相等時取0，不等時取1。最終算得矩陣D的右下角元素dm,n即為故障鏈序列Cx與Cy之間的ED，dm,n越大代表Cx與Cy之的差異性越大。

當故障鏈序列長度不一致的時候，長序列之間的ED將遠大于短序列之間的ED，因此需要對ED進行歸一化處理：

(10)

歸一化后的ED能較為準確地度量具有不等長、離散性等特點的故障鏈相似性，提高后續聚類分析的準確性與數據挖掘的效率。

2.2 基于AGNES算法的故障鏈聚類

文中采用凝聚式層次聚類(AGglomerative NESting,AGNES)算法[21]，根據2.1節所得的故障鏈間的ED，完成對故障鏈集合的聚類分析。

AGNES算法“自底而上”的聚類過程如圖3所示。隨著ED的增加，故障鏈序列逐漸合并，直至最后聚至同一類中。聚類簇數可通過改變截取閾值來靈活調整，而最優聚類簇數可通過Calinski-Harabaz(CH)指標[22]進行評估求取。其中，S為由故障鏈Cj組成的故障鏈集合。

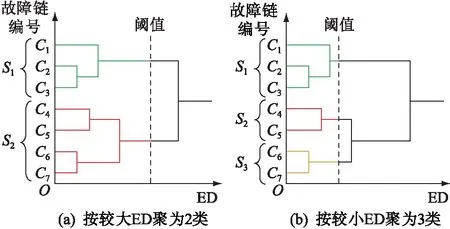
圖3 層次聚類Fig.3 Tree diagram of hierarchical clustering

以CH指標較高的簇數對故障鏈集合進行劃分后，同集合內故障鏈相似度較高，即線路開斷的先后次序相近，則可近似認為此類故障鏈在同一連鎖故障演化模式下產生。對各類故障鏈集合分別進行關鍵線路辨識，找出各連鎖故障演化模式下具有推波助瀾作用的薄弱環節，能有效提高辨識精度。

3 連鎖故障關鍵線路辨識

3.1 線路風險重要度

假設故障鏈集合S共有m條故障鏈，其中有h(h≤m)條故障鏈包含線路Li，即滿足：

Li∈Cjj=1,2,…,h

(11)

則線路Li的風險重要度的計算公式為：

(12)

式中：ω(Li,Cj)為線路Li在故障鏈Cj中的重要度權重。考慮到最終負荷損失是由故障鏈中所有線路開斷造成的，且連鎖故障演變過程存在級聯性，因此認為先開斷線路對負荷損失的影響高于后開斷線路，相應權重也更高。文中假設重要度權重隨開斷順序按指數分布遞減，則計算公式為：

ω(Li,Cj)=e-μ(X(Li,Cj)-1)

(13)

式中：X(Li,Cj)為線路Li在故障鏈Cj中的順序；μ為調節系數，用于調整重要度權重遞減的速度，μ越小，故障鏈中的線路權重分布就越均衡。當μ=0.1時，按開斷順序算得的權重依次為1.000，0.915，0.819，0.741，0.670等。

綜合來看，線路所涉及的連鎖故障越多、引起的故障越嚴重、開斷順序越靠前，則對應的線路風險重要度也會更高。按I(Li)對所有線路進行排序，排名靠前的線路即為連鎖故障演化過程中的關鍵線路。

3.2 關鍵線路辨識流程

關鍵線路辨識流程如圖4所示。首先通過改進DCSS模型生成故障鏈集合，然后計算故障鏈之間的ED，并通過選取合適的ED閾值，應用AGNES算法完成對故障鏈的聚類，分別計算出同類故障鏈集合中各線路的風險重要度，識別出各類故障演化模式下的關鍵線路。

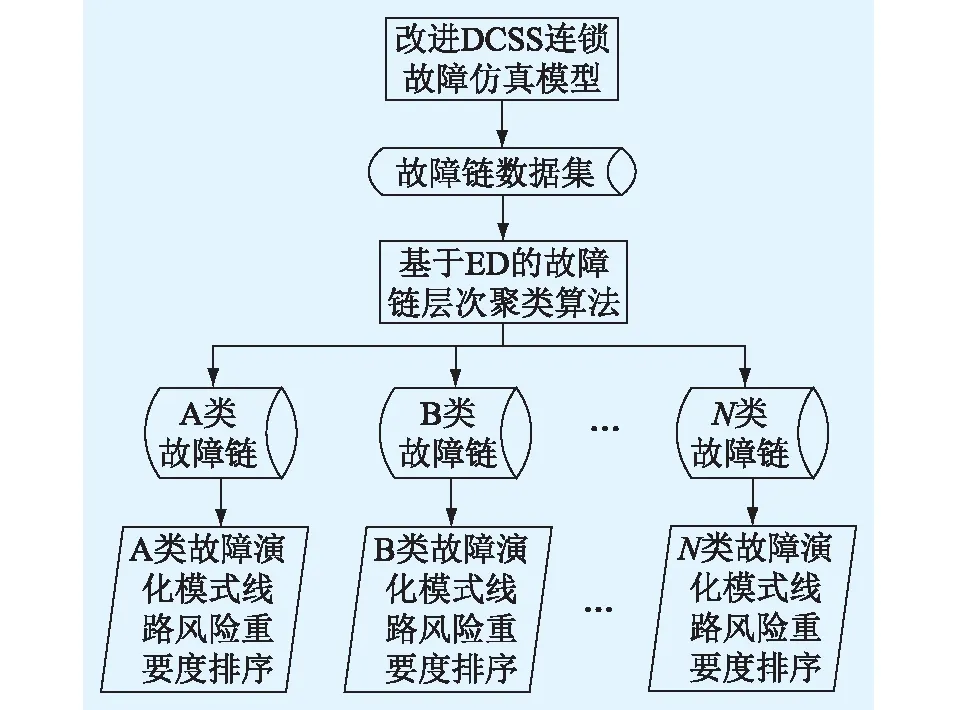
圖4 關鍵線路辨識流程Fig.4 Flow chart of critical line identification

4 算例分析

為了進一步證明文中算法在大電網中的有效性，文中采用Matpower軟件包中的算例case2383wp進行仿真研究，該算例的詳細數據參見文獻[23]。

4.1 故障鏈集合生成

文中采用抽樣效率較高的RC法，通過調用改進DCSS連鎖故障仿真程序對Matpower軟件包中的2 383節點模型(滿足“N-1”準則)進行模擬。

2 383節點模型數據不包含線路平均故障頻率等參數，因此文中將IEEE RTS-79可靠性標準測試模型的架空線故障率隨機映射至文中模型的2 896條線路上，使得2個模型的線路故障率概率密度分布函數f(P)相近，如圖5所示。

圖5 RTS-79與文中模型的線路故障率概率密度曲線對比Fig.5 Comparison of line failure rate probability densityfunction of RTS-79 and the model in this paper

將映射所得的故障率與實際線路長度相乘得到平均失效頻率λ之后，根據式(5)可算得相應線路的不可用率U(Linit,i)，其中線路平均修復時間tDur取IEEE RTS-79標準數據的中位值10 h。

為平衡故障鏈搜索時間與搜索廣度，文中以負荷損失超過2 701 MW(占總負荷的10%)為篩選閾值，經過10萬次RC法循環仿真，共生成424條由不同N-2初始故障引發的故障鏈。對所生成的故障鏈進行線路頻次統計，統計情況如表1所示。

表1 故障鏈集合中線路出現頻次統計Table 1 Frequency statistics of occurrence of lines in fault chain set

由表1可知，僅有極少數線路在故障鏈集合中出現超過300次，而同時有多達397條線路出現小于27次。線路的頻次分布具有明顯的“長尾效應”，即故障鏈集合中很少一部分線路的出現次數遠高于其他線路，表明這些線路與嚴重連鎖故障的觸發與演化存在密切關系。

4.2 故障鏈聚類結果

對4.1節所得的故障鏈集合采用ED算法，根據424條故障鏈之間的相似性可繪制出如圖6所示的熱力圖。以故障鏈間的ED為依據進行層次聚類，可得如圖7所示的聚類過程樹狀圖。

圖6 故障鏈相似性熱力圖Fig.6 Fault chain similarity heat map

圖7 故障鏈集合層次聚類Fig.7 Hierarchical clustering of fault chain set

不同簇數的聚類方案所得的CH評估指標如圖8所示，由圖8可知，當簇數為3時，CH指標最高，表明相應的聚類方案最優。3類故障鏈已在圖7中以不同顏色標注，分別記為故障鏈集合①～③，同類集合中的故障鏈相似性較高，表明所涉及的連鎖故障演化路徑重合度較高。

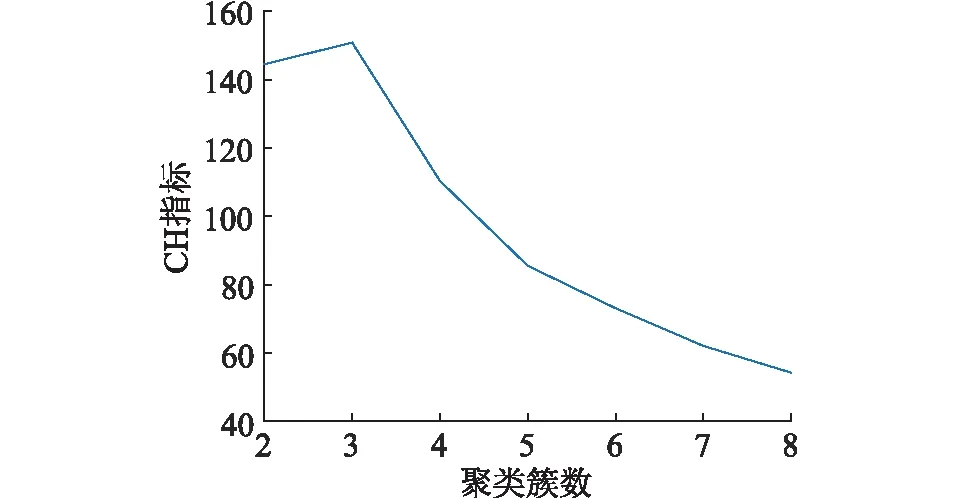
圖8 不同聚類簇數對應的CH指標Fig.8 CH index corresponding to different cluster numbers

4.3 關鍵線路辨識

對故障鏈集合①～③分別進行信息統計，所得結果如表2所示，其中平均故障鏈長度是指集合內每條故障鏈所開斷線路條數的平均值。

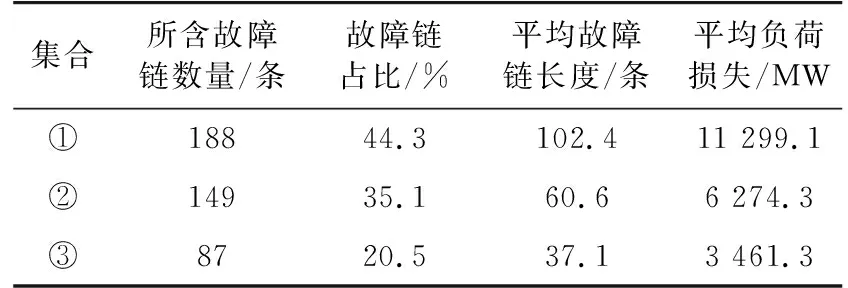
表2 不同故障鏈集合的基本信息統計Table 2 Basic information statistics of different fault chain sets

根據式(12)—式(13)分別計算各故障鏈集合中的線路風險重要度I(Li)，調節系數μ取0.1。將所有線路按I(Li)進行降序排列，排名靠前的線路即為相應故障鏈集合中的關鍵線路。表3中分別列出了聚類前后各類故障鏈集合中線路風險重要度排名前5的關鍵線路，括號內的數字表示對應線路在未聚類時故障鏈總集合中的重要度排名。

表3 不同故障鏈集合中的關鍵線路排序Table 3 Critical lines rank in different fault chain sets

結合表2、表3可知，由于故障鏈集合①中的故障鏈占比較大(44.3%)，若直接對未聚類的故障鏈總集合進行關鍵線路辨識，前5名分別為{L15,L96,L680,L113,L8}，此結果與故障集合①中的關鍵線路前5名{L15,L96,L113,L24,L680}高度重合，但故障鏈集合②與③中的關鍵線路在未聚類故障鏈總集合中的排名普遍較低，意味著若不進行聚類極有可能造成故障鏈集合②與③中關鍵線路的漏選。

4.4 辨識結果有效性驗證

文中參考文獻[24]，對算法所辨識的關鍵線路進行容量擴建，并基于相同的初始故障集重新進行連鎖故障仿真，擴容后故障鏈集合的連鎖故障風險R(S)下降得越多，證明相應算法所辨識的線路在故障鏈集合中的重要性越高。

線路容量的調整在實際系統中可通過更換線路、增加并行線路等措施實現[25]。在文中的算例中，線路擴建容量設定為額定容量的2倍，根據4.3節的關鍵線路辨識結果分別設置以下2組擴容方案。

(1) 擴容方案一。按未聚類時的辨識結果取線路風險重要度排序的前3名，具體擴容線路為{L15,L96,L680}。

(2) 擴容方案二。按聚類后的辨識結果分別取各故障鏈集合中的線路風險重要度排序第1名，具體擴容線路為{L15,L250,L169}。

另設置隨機擴容方案，即隨機選取3條故障鏈集合中所涉及的線路進行擴容。

對上述3種方案擴容后的2 383節點系統重新進行424組連鎖故障仿真并進行風險評估，其中隨機擴容的連鎖故障風險由20次仿真后取平均值所得，原系統及3類方案下的風險如圖9所示。

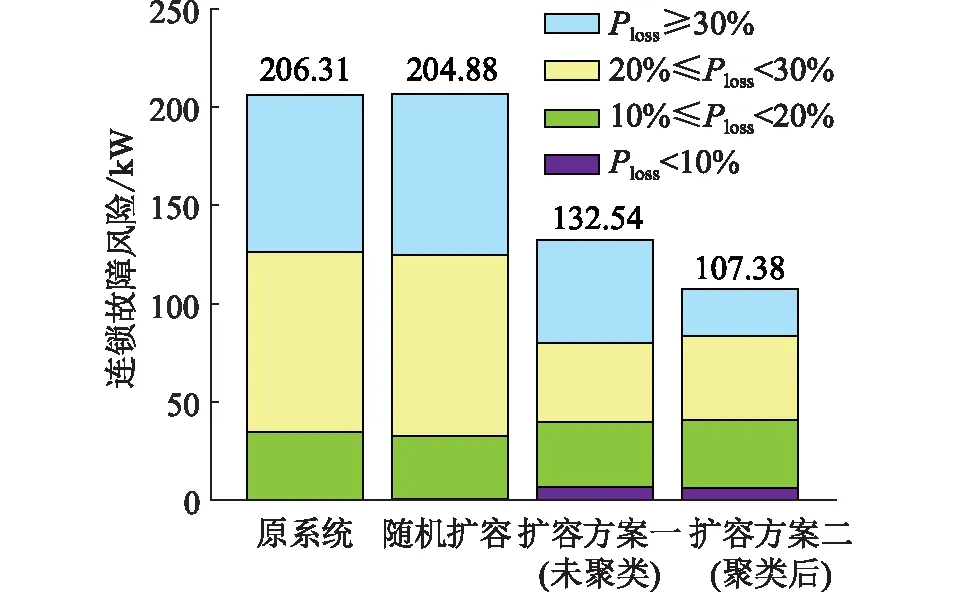
圖9 不同擴容方案下系統連鎖故障風險比較Fig.9 Comparison of system cascading failure risks under different expansion plans

由圖9可知，上述的3種擴容方案將連鎖故障整體風險由206.31 kW分別降至204.88 kW，132.54 kW，107.38 kW。隨機擴容方案下，整體風險平均僅降低了1.43 kW，證明隨機選取的線路重要性較低。這是因為線路的重要性分布與4.1節所述的頻次分布類似，皆具有“長尾效應”，隨機選取線路大概率為重要性不高的非關鍵線路。而在基于線路風險重要度排序的2種擴容方案中，方案二能最大程度地降低連鎖故障風險，其中Ploss≥30%的大規模連鎖故障風險由79.8 kW減少至24.1 kW，明顯低于方案一的52.6 kW，證明分類辨識所得關鍵線路的重要性更高。

為進一步探究辨識結果對連鎖故障風險的影響，按故障鏈集合①～③對原系統及擴容方案一、二下的連鎖故障風險進行分類統計，對比結果如表4所示，其中，括號內表示相較于原系統連鎖故障風險下降的百分比。

由表4可知，在未聚類時，方案一使得故障鏈集合①中的連鎖故障風險下降了50.7%，但同時僅讓故障鏈集合③的連鎖故障風險降低了0.36%。因此未聚類時所辨識的線路對大規模故障鏈集合而言重要性較高，對其他規模較小故障鏈集合的影響力則相對有限。相比之下，方案二下的整體風險下降了48.0%，故障鏈集合①～③的風險分別下降了58.6%，74.4%，11.0%，皆優于方案一，證明分類辨識的線路集合{L15,L250,L169}在各類集合中的重要程度皆高于未聚類前的辨識結果。

上述結果說明，若直接對未聚類的424條故障鏈進行關鍵線路辨識，辨識結果將傾向于占比較大的故障鏈集合，難以全面顧及各類連鎖故障演化模式，所辨識的線路在規模較小集合中的重要性也相對較低。相比之下，基于故障鏈聚類算法的分類辨識結果使得各類連鎖故障風險的下降程度更高，進一步證明了故障鏈聚類算法對于提高關鍵線路辨識效果的有效性。

4.5 與其他關鍵線路辨識算法的比較

為進一步驗證文中所提關鍵線路分類辨識算法的有效性，文中針對2 383節點模型采用潮流介數法[26—27]與連鎖故障關系圖(cascading failure graph，CFG)法[25]，分別得到線路重要性排序，根據排序結果前3名分別設置相應的線路擴容方案。其中潮流介數法具體擴容線路為{L169,L52,L23}，CFG法具體擴容線路為{L8,L38,L90}。對擴容后的系統重新進行仿真與連鎖故障風險評估，所得結果與4.4節的擴容方案一、二比較，對比結果如圖10所示。

由圖10可知，由于潮流介數法未考慮連鎖故障的演化過程，因此辨識結果對降低系統連鎖故障風險的作用較小；CFG法與文中所提方法(未聚類)雖能一定程度降低系統連鎖故障風險，但缺乏對各類連鎖故障演化模式的綜合考慮，作用依然有限；相比之下，基于故障鏈聚類的關鍵線路擴容方案能夠最大程度地降低系統的連鎖故障風險，證明文中方法(聚類后)所辨識線路的重要程度更高。

5 結語

文中首先建立了改進DCSS仿真模型，并對過載主導型連鎖故障進行仿真，生成含豐富時序信息的故障鏈集合。針對現有關鍵線路辨識算法未能對各類故障演化模式予以全面考慮的不足，文中提出了基于ED的故障鏈聚類算法，對相似度較高的故障鏈集合進行分類評估，能夠更加精確地揭露特定演化路徑下的薄弱環節，可進一步提高關鍵線路的辨識精度與效率。以Matpower 2 383節點系統為例，通過對關鍵線路進行擴建，以擴容前后的連鎖故障風險水平為依據，量化比較了各類算法所辨識線路的重要性，進一步證明了所提模型及算法的有效性。文中的研究工作還可從以下方面進一步完善和深入：

(1) 隨著高壓直流的投運及大量電力電子器件在電力系統中應用，連鎖故障過程中的無功問題、交直流耦合問題日益突出，基于更復雜模型及其故障鏈數據集的關鍵線路辨識將是后續研究的要點。

(2) 文中從故障演化路徑相似性的角度進行聚類，后續可進一步考慮如失負荷量、系統解列程度等其他變量作為聚類依據。