多通道長短期記憶卷積網絡的風速預測

修春波， 蘇歡， 蘇雪苗

(天津工業大學控制科學與工程學院，天津 300387)

0 引言

風能作為一種清潔、無污染的可再生能源得到了快速開發和應用，而大規模風電并網是風能利用最有效的途徑之一。但風能具有明顯的間歇性、波動性，因此風電具有較強的不確定性、隨機性和不可控性[1—3]，風電會對電網產生較大的沖擊，甚至影響電網的穩定運行。通過對風速進行有效預測，及時調整調度計劃，能夠有效減少電力系統備用容量，降低風電成本，改善電能質量[4—6]。因此，風速預測一直是風電領域的研究熱點之一。

風速序列的預測方法較多[7—11]，主要分為基于數值氣象預報的預測方法和基于歷史數據的預測方法。前者根據實際的氣象條件，如溫濕度、風向、氣壓等數據，利用氣象預報模型實現風速預測。而后者是從歷史數據序列中提取蘊含的規律信息，由此實現對未來數據的預測。如持續預測法是早期的一種較實用有效的風速序列預測方法，但其預測機理過于簡單，預測準確性較低。隨著研究的深入，時間序列分析法[12]、神經網絡法[13]、卡爾曼濾波法[14]、支持向量機(support vector machine,SVM)法[15]以及混沌理論[16]等都被應用于風速序列的預測分析中，改善了風速序列的預測性能。但這些方法均涉及到一個難以確定的關鍵參數，即被預測風速與歷史輸入數據的關聯長度。歷史關聯數據過長會導致陳舊冗余的信息影響預測結果，而歷史關聯數據過短則會導致信息丟失或不足，同樣會降低預測性能。在實際應用中，通常采用經驗法或根據相空間重構理論進行構造，但對于混沌特性不明顯的風速序列，樣本的構造方式缺少相應的理論指導，預測性能不穩定。

近年來，深度學習理論發展迅速，在時間序列預測分析領域中表現出優異的應用性能[17—18]。例如，基于深度學習的循環神經網絡(recurrent neural network，RNN)可應用于時間序列預測分析的求解中[19—20]，但該網絡存在梯度消散和梯度爆炸等問題。為此，可采用長短期記憶(long short-term me-mory，LSTM)網絡模型[21]實現時間序列的預測分析。LSTM網絡結構獨特，是RNN的改進網絡，對時間序列預測分析問題具有很好的求解性能[22—25]。盡管深度學習網絡能夠利用大數據樣本獲取時間序列中的規律信息，但預測數據關聯長度等參數仍須人為選定，這限制了深度學習網絡在風速序列預測中的應用性能。

為了避免不恰當的關聯數據長度等影響網絡預測性能，提出一種多通道LSTM網絡與一維卷積神經網絡相結合的風速序列預測方法。該方法通過構建多通道LSTM子網絡獲得與不同輸入數據長度相關的風速序列計算值，對各LSTM子網絡的輸出值進行一維卷積操作，并利用全連接網絡層輸出預測值。同時，為了避免預測過程中可能出現的誤差累積及漂移，對預測值進行誤差補償修正，進一步提高預測精度，改善風速預測性能。

1 LSTM網絡模型

通常，實際時間序列中各個數據點之間具有時間上的順序關聯性。采用傳統的前向型神經網絡進行時間序列預測分析時，時間序列中數據點之間的順序關聯性只能體現在構建的訓練樣本中，而網絡自身結構中不具有體現數據點時間順序關聯性的機制。相比而言，RNN利用隱藏層節點之間的連接，能夠很好地描述時間序列中數據之間的順序關聯性，從結構上更符合時間序列預測要求。但RNN對序列信息的利用缺少選擇性，當序列長度過長時會出現梯度消散的問題，因此，RNN不適合用于復雜時間序列的預測分析。

LSTM網絡模型是一種改進的RNN模型，解決了梯度消散問題，利用門結構實現了對序列信息的選擇性利用，適合復雜時間序列預測問題的求解。LSTM網絡模型的基本單元如圖1所示。

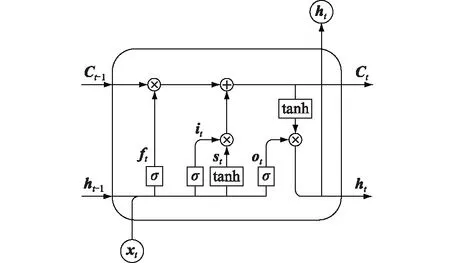
圖1 LSTM網絡模型的基本單元Fig.1 Basic unit of LSTM network model

圖中，ft，it，ot分別為遺忘門、輸入門和輸出門的狀態；st為輸入節點狀態；ht，ht-1分別為當前時刻和前一時刻的輸出；xt為當前序列的輸入；Ct，Ct-1分別為當前時刻和前一時刻記憶單元的狀態信息。LSTM網絡的基本單元中包含了門結構和記憶單元，利用遺忘門、輸入門、輸出門可實現記憶單元信息的添加或刪除。LSTM網絡基本單元的輸入包含xt，Ct-1以及ht-1。在遺忘門中，xt和ht-1共同決定Ct-1的遺忘部分。在輸入門中，xt，ht-1經過Sigmoid和tanh函數變換后共同決定當前記憶單元狀態信息的更新部分。通過遺忘門和輸入門，將Ct-1更新為Ct。在輸出門中，xt和ht-1經過Sigmoid函數變換得到ot，Ct經過tanh函數變換后和ot共同組成ht。該單元的具體計算過程如下：

ft=σ(Wf·[ht-1,xt]+bf)

(1)

it=σ(Wi·[ht-1,xt]+bi)

(2)

st=tanh(Ws·[ht-1,xt]+bs)

(3)

Ct=ft°Ct-1+it°st

(4)

ot=σ(Wo·[ht-1,xt]+bo)

(5)

ht=ot°tanh(Ct)

(6)

其中，[ht-1,xt]表示將ht-1和xt這2個列向量拼接成1個列向量，即：

(7)

Wf，bf分別為遺忘門的權重系數矩陣和偏置項；Wi，bi分別為輸入門的權重系數矩陣和偏置項；Ws，bs分別為輸入節點的權重系數矩陣和偏置項；Wo，bo分別為輸出門的權重系數矩陣和偏置項；σ(·)和tanh(·)分別為Sigmoid函數和雙曲正切函數。式(4)和式(6)中“°”表示按元素乘運算。

遺忘門和輸入門是LSTM網絡基本單元的核心結構，能夠使網絡更有效地保持長期記憶。一般來說，網絡輸入數量的多少表明了網絡輸出值與歷史數據的關聯長度。由于風電場風速序列的形成機理復雜，未來風速值與歷史數據的關聯長度難以人為有效確定，即網絡的輸入數據數量不容易有效確定，輸入數據量較少時會造成信息丟失，輸入數據較多時會造成信息冗余，均會降低模型的預測性能。為此，文中針對風速序列預測問題，結合卷積網絡結構，構建對輸入數據量具有一定適應性的多通道LSTM網絡預測模型，實現預測特征信息的有效提取。

2 多通道LSTM網絡預測模型

2.1 網絡結構

作為一種氣象數據，風速時間序列通常短期可預測、長期難以預測，且預測值與歷史數據的關聯長度也很難利用先驗知識進行選取。為提高預測模型的有效性，構建多個具有不同輸入長度的LSTM子網絡，并利用卷積網絡將各子網絡的輸出進行結合，從而構成多通道LSTM網絡預測模型。例如，對預測步長為n的風速序列預測問題，多通道LSTM預測網絡與卷積網絡(multi-channel LSTM and convolution neural net-work，MCLSTM-CNN)相結合的預測模型結構如圖2所示。

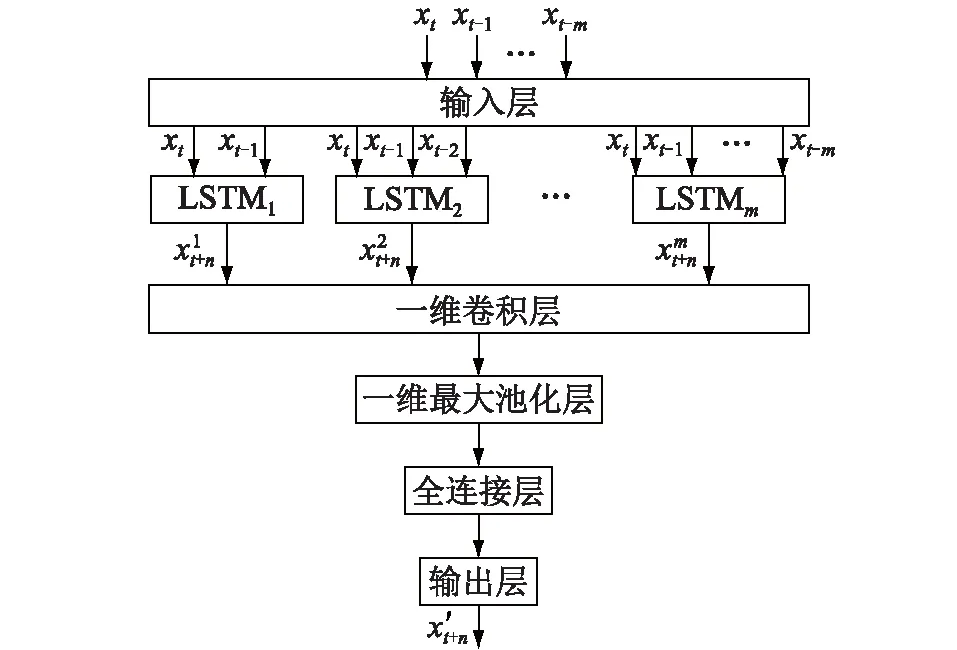
圖2 MCLSTM-CNN網絡模型Fig.2 MCLSTM-CNN network model

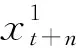
將網絡第一部分中m個LSTM子網絡輸出的風速預測值構成一維信號，作為一維卷積神經網絡的輸入，卷積網絡中卷積操作的卷積核大小為2，最大池化操作的池化窗口大小為2。使用卷積網絡對一維信號進行特征提取，最后通過全連接層輸出最終的風速預測值x′t+n。

一維卷積神經網絡是一種用于處理時序數據等一維信號的特殊神經網絡，由卷積層、池化層和全連接層組成。卷積層利用權值共享和不同尺度的卷積核可以實現網絡所需特征的自動提取。池化層則從卷積層中提取到主要的特征，并在時間維度上進行降維操作，減小數據計算量。全連接層對全局特征進一步抽象組合，得到最終輸出預測值。

上述預測模型利用卷積層實現了預測信息的自動提取，避免了單一LSTM網絡輸入數據量等參數須人為選取的問題。當模型輸入歷史數據長度足夠，即m值足夠大時，模型就能夠利用歷史數據構成的訓練樣本自動實現網絡參數的調整，并確定各子網絡的預測權重，從而有效提高網絡的泛化能力，改善網絡的預測性能。

2.2 誤差補償法

隨著預測過程的進行，誤差累積及漂移不可避免，為此，對網絡預測結果進行動態誤差補償來進一步減小預測誤差。

對于預測步長為n的風速序列預測問題，利用MCLSTM-CNN模型連續預測可得到各個時刻的預測值，設t-n時刻，t時刻，t+n時刻的預測值分別為x′t-n，x′t，x′t+n，則對x′t+n進行動態預測誤差補償，得到最終的預測結果x″t+n為：

x″t+n=x′t+n+γ(t)e(t)

(8)

式中：e(t)=xt-x′t，為t時刻的網絡預測誤差；γ(t)為動態補償系數，其值根據補償結果誤差的負梯度方向進行調整，即滿足式(9)—式(11)。

(9)

E(t)=(x″t-xt)2

(10)

x″t=x′t+γ(t-n)e(t-n)

(11)

式中：η為動態調整步長；E(t)為步長結果誤差；x″t為t時刻序列點的最終預測結果。

根據歷史預測誤差漂移情況，對第n步預測結果進行動態誤差補償，能夠在一定程度上有效克服連續預測過程中出現的誤差累積漂移問題，從而進一步提高風速序列預測的有效性。

3 風速預測仿真實驗與結果分析

3.1 數據集與預處理

選取某風電場檢測的風速數據進行預測分析，風速數據的采樣間距為15 min,以時間先后為序構成風速數據集。該風速數據集的最大風速為18.72 m/s，最小風速為0.91 m/s。將數據集中前90%的數據作為訓練樣本，用于網絡模型的訓練，后10%的數據作為測試樣本，用于測試網絡模型的預測性能。

采用min-max方法對數據進行歸一化處理，將風速數據的數值映射到[0，1]內，歸一化計算方式為：

(12)

式中：xi為第i個數據歸一化后的數值；yi為第i個數據歸一化前的數值；ymax為數據集中的最大值；ymin為數據集中的最小值。

采用3種評價指標評價模型的預測性能，分別為均方根誤差(root mean square error，RMSE)，平均絕對誤差(mean absolute error，MAE)，平均絕對百分比誤差(mean absolute percentage error，MAPE)，其計算如下：

(13)

(14)

(15)

式中：N為預測數據總個數；y″i為第i個數據的預測值。

3.2 實驗結果與分析

分別采用具有預測誤差補償(error com-pen-sation，EC)的MCLSTM-CNN預測模型(MCLSTM-CNN-EC)、SVM、反向傳播神經網絡(back pro-pa-ga-tion neural network,BPNN)、LSTM[23]、卷積循環神經網絡[20](convolutional recurrent neural network,CRNN)、MCLSTM預測模型以及未進行誤差補償的MCLSTM-CNN預測模型對風速序列進行超短期預測分析對比實驗。其中，CRNN模型采用一維卷積神經網絡先對輸入風速序列進行特征提取，再利用LSTM網絡對風速值進行預測輸出。MCLSTM模型采用文中所提出的多通道LSTM子網絡直接與全連接層相結合，即省去了卷積層與池化層。

設預測步長n為16，即對4 h后的風速值進行預測分析。選取歷史輸入序列長度為10，即上述各預測模型的輸入層神經元個數均為10，輸出層神經元個數均為1。預測模型的訓練批次大小為32，訓練迭代次數為300次，將歸一化后數據的均方誤差作為損失函數，優化算法為Adam算法。

MCLSTM-CNN模型訓練過程中損失函數值隨迭代次數的變化如圖3所示。

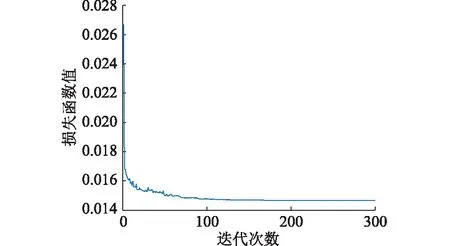
圖3 MCLSTM-CNN在數據集上訓練時的損失函數Fig.3 Loss function of MCLSTM-CNN on dataset

由圖3可見，預測網絡能在300次迭代內完成參數訓練。圖4為上述各預測模型的預測結果。圖5為圖4的局部預測結果(前150個預測數據)。

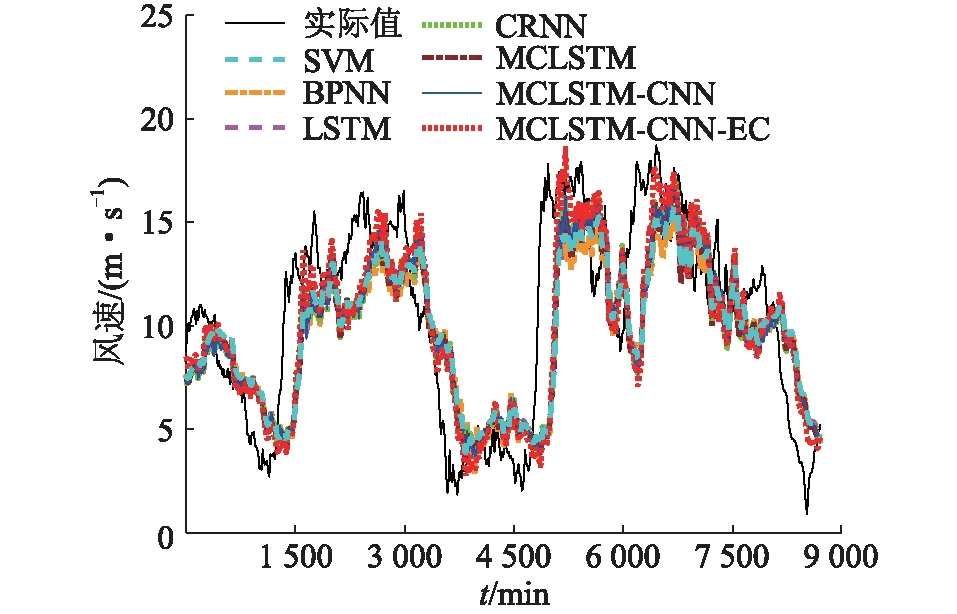
圖4 各預測模型的預測結果Fig.4 Prediction results of each prediction model

由上述預測結果可見，雖然各種預測方法相對于實測數據均出現了一定的滯后現象，但MCLSTM-CNN-EC的預測曲線與實測數據具有更好的擬合度，表現出更好的預測性能。

表1和表2分別為圖4與圖5所示預測結果的誤差評價指標。

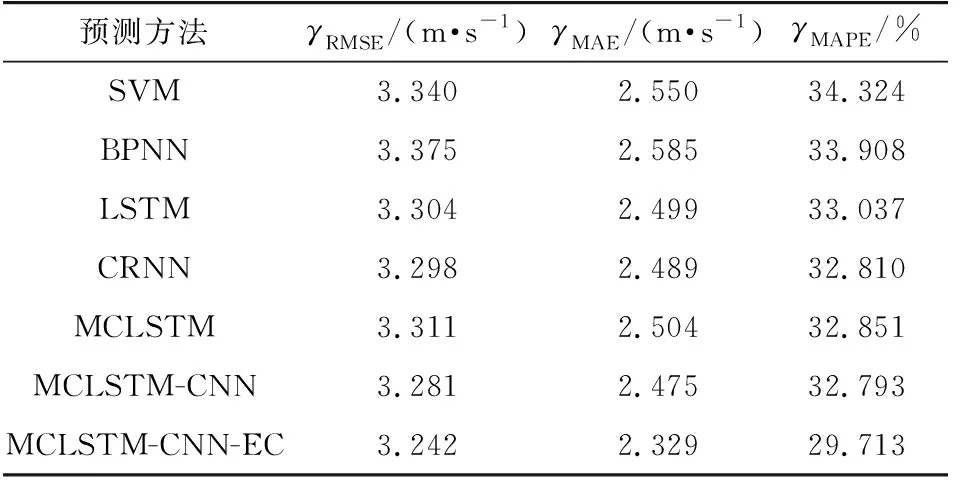
表1 數據集的預測誤差指標Table 1 Prediction errors of dataset

表2 數據集前150個預測數據的預測誤差指標Table 2 Prediction errors of the first 150 prediction results of dataset

由上述預測結果以及預測評價指標可知，基于深度學習的LSTM網絡和CRNN模型的預測性能優于傳統BPNN和SVM模型，說明基于深度學習的預測網絡對歷史數據信息具有更強的預測特征提取能力，可有效提高風速序列的預測精度。而CRNN模型利用卷積神經網絡提取風速序列的深度特征信息，以此為基礎利用LSTM模型進行預測，與單一的LSTM網絡相比，CRNN模型具有更好的預測性能。MCLSTM-CNN模型利用多通道LSTM子網絡結構實現不同關聯數據長度信息的提取，可有效提高模型對預測序列的適應性，根據子網絡的輸出，利用卷積層自動提取預測信息，能夠從歷史數據中獲得適合序列預測的特征參數，避免了輸入數據長度參數難以選取的問題，因此，預測結果相比于LSTM、CRNN等預測模型更優。同時，MCLSTM-CNN模型在各項誤差指標上也優于缺少卷積層和池化層的MCLSTM模型。可見，MCLSTM-CNN模型中的一維卷積神經網絡能更好地提取多通道LSTM子網絡的特征信息，說明了MCLSTM-CNN模型結構的合理性。在此基礎上，MCLSTM-CNN-EC方法對MCLSTM-CNN模型輸出的預測值進行動態誤差補償，克服了預測過程中產生的誤差累積與漂移，因此其各項預測誤差指標明顯降低，預測性能得到了進一步改進。在上述的各種網絡模型中，MCLSTM-CNN-EC模型具有最優的預測性能和良好的泛化能力，可有效提升風速的超短期預測精度。

4 結語

針對風速序列超短期預測問題，提出了多通道LSTM子網絡與一維卷積神經網絡相結合的預測模型。利用多個LSTM子網絡實現基于不同歷史數據長度的風速序列預測計算，采用一維卷積網絡對各子網絡的計算結果進行特征信息的自動提取，得到網絡的預測值，利用動態誤差補償方法對網絡預測值進行校正，能夠有效克服預測過程中所產生的誤差累積與漂移。該方法在風速序列超短期預測中表現出良好的預測性能，實驗對比結果驗證了該網絡結構的合理性。文中方法研究了基于歷史數據信息的風速預測方法，為進一步提升風速預測有效性，未來可開展結合數值氣象預報信息的深度學習風速預測方法研究，從而提升風電并網的性能。