基于廣義Kelvin 鏈鋼管混凝土徐變研究

楊 超，陳夢成，張明陽,3，李 騏，方 葦，溫清清

(1.華東交通大學土木建筑學院，南昌 330013；2.軌道交通基礎設施性能監(jiān)測與保障國家重點實驗室，南昌 330013；3.江西交通職業(yè)技術學院建筑工程系，南昌 330013)

鋼管混凝土結構因優(yōu)越力學性能已被廣泛使用在高層和超高層建筑、橋梁、地鐵車站等土木工程基礎設施中，相關最新研究層出不窮[1-5]。核心混凝土徐變對鋼管混凝土結構性能具有重要影響，鋼管與混凝土組合效應使得分析該結構時變性能問題更為困難。因此，鋼管混凝土徐變研究具有重要理論和實踐意義[6-7]。

鋼管內核心混凝土受力狀態(tài)復雜，為三向應力狀態(tài)。國內外至今仍然沒有對鋼管混凝土徐變計算提出一個統(tǒng)一的計算方法。因此，鋼管混凝土徐變研究依然是目前研究熱點。韓林海等[8-9]采用試驗和有限元計算相結合的方法，討論了氯離子侵蝕和長期荷載耦合作用下鋼管混凝土力學性能問題，陳寶春等[10]建立了鋼管混凝土拱橋徐變預測模型，王玉銀等[11]采用試驗技術和有限元分析方法討論了鋼管混凝土非線性徐變問題，郝兆峰等[12]采用試驗方法探討了帶缺陷鋼管混凝土的徐變問題，劉偉等[13]對鋼管再生混凝土徐變問題進行了試驗研究，肖思柯等[14]研究了考慮非線性徐變的鋼管混凝土柱穩(wěn)定承載力計算問題，丁敏等[15]建立了鋼管混凝土軸心構件徐變預測模型，并用該模型進行了徐變性能分析。

上述研究在討論鋼管混凝土徐變問題時，大多都是以單向應力狀態(tài)混凝土徐變模型為基礎。事實上，正如前文所述，鋼管核心混凝土受力狀態(tài)為三向應力狀態(tài)，徐變性能復雜。試驗表明[16-17]，在三向應力狀態(tài)下，應該考慮徐變Poisson 效應。三向應力作用下徐變不能用單向應力作用下徐變規(guī)律推算，應該考慮三向應力的相互作用。近年來，有不少文獻論證這一觀點[18]。王元豐等[19]在在分析鋼管混凝土徐變試驗數(shù)據(jù)后，認為若要準確計算鋼管混凝土徐變，需要對現(xiàn)有基于單軸應力徐變試驗得到徐變模型進行修正，并建立了相應的計算模型；Li 等[20]和張電杰等[21]引入徐變泊松比效應[22]，討論了鋼管混凝土徐變的計算方法。然而，目前三向應力狀態(tài)下混凝土徐變的研究仍不成熟[23-24]。

本文根據(jù)粘彈性理論和徐變疊加原理，采用多參數(shù)Kelvin 元件鏈粘彈性模型，建立三維應力狀態(tài)下的鋼管混凝土徐變計算方法，并嵌入有限元軟件Ansys 中，用Fortran 語言編程，建立相應有限元數(shù)值分析模型。模型參數(shù)近似表示為連續(xù)粘滯譜。為驗證該方法的可行性和有效性，本文還將進行鋼管混凝土徐變試驗。

1 單向應力狀態(tài)下混凝土徐變本構模型

根據(jù)粘彈性理論[25]，單向應力作用下混凝土徐變可表示成第一類Volterra 積分方程：

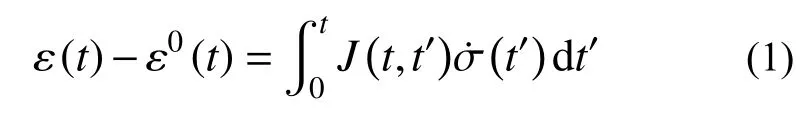
式中：t為混凝土齡期；t′為荷載齡期；σ為應力；ε為應變；ε0(t)為非彈性應變(除作用力以外如溫度引起的熱膨脹和收縮等產生的應變)，本文假定ε0(t)=0；J(t,t′)為徐變函數(shù)(也稱為徐變柔度函數(shù))，定義為單位應力作用下t-t′時間內引起的總應變。它可表示為Dirichlet 級數(shù)形式[25]：

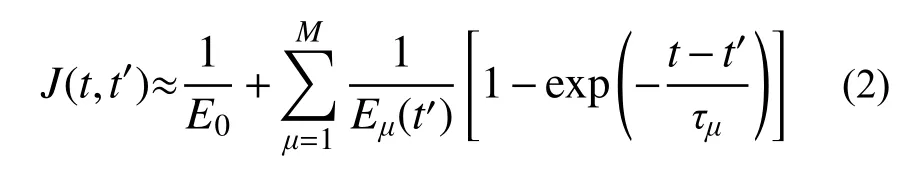
式中，第1 項可以理解為一個牛頓彈性元件在單位力作用下引起的彈性應變，第2 項可以理解為M個Kelvin 元件在單位力作用下引起的總應變，如圖1 所示。Kelvin 元件個數(shù)M的選取取決于混凝土徐變計算精度，一般來說，M取得越大，精度越高；E0為彈性模量；τμ為粘滯時間；Eμ(t′)為荷載齡期相關瞬時彈性模量，由連續(xù)粘滯譜A(τμ)表示[25]：

圖1 廣義Kelvin 混凝土徐變模型Fig.1 Generalized Kelvin chain for concrete creep model

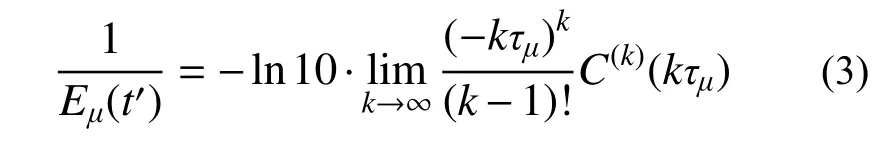
式中：C(k)(kτμ)為徐變度C(t,t′)對t的k階導數(shù)；C(t,t′)=J(t,t′)-1/E0；經驗表明：當k=3 的時候，計算可滿足精度要求。

將式(3)代入式(1)中第一式，可得：

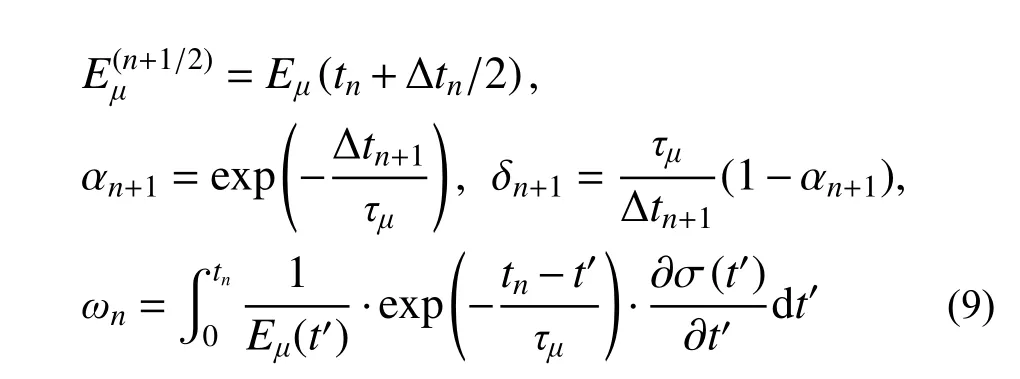
式(8)與文獻[26]用率型法得到的結果完全一致。

通過分步積分法，式(9)中最后一式ωn可以進一步改寫為：

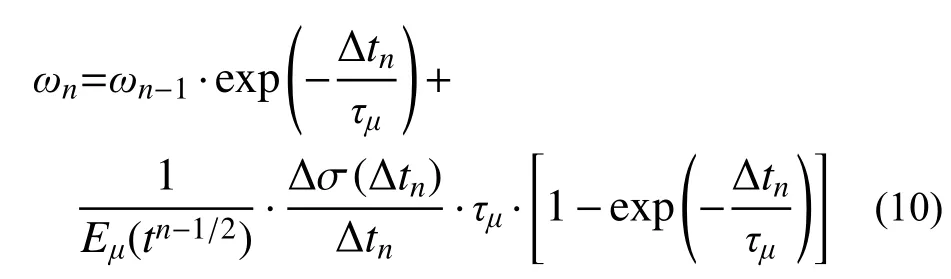
式中，ω0=0。

將式(8)代入式(4)，得到單向應力狀態(tài)下考慮混凝土徐變的總應變增量為：

式(12)即為單向應力狀態(tài)下混凝土徐變應力應變增量本構關系。

2 鋼管混凝土徐變本構模型

對鋼管混凝土結構而言，核心混凝土的徐變應力狀態(tài)具有明顯的三向特性。目前，國內外對三向應力狀態(tài)下的混凝土徐變的研究尚未成熟，沒有可直接借鑒的三向應力狀態(tài)下徐變計算模型。因此，本文參考Neville 等[16]、王元豐和韓冰等[18]以及李世偉和楊永清等[24]做法，擬采用泊松比效應，把單向應力狀態(tài)下混凝土徐變計算模型推廣到三向應力狀態(tài)。假定三向應力狀態(tài)下，三個方向徐變泊松比分別為μc1、μc2和μc3，則根據(jù)應力-應變彈性本構關系，可得到如下轉換矩陣：

對于鋼管混凝土結構而言，軸向荷載作用下，根據(jù)彈性力學理論，式(15)可進一步改寫為：

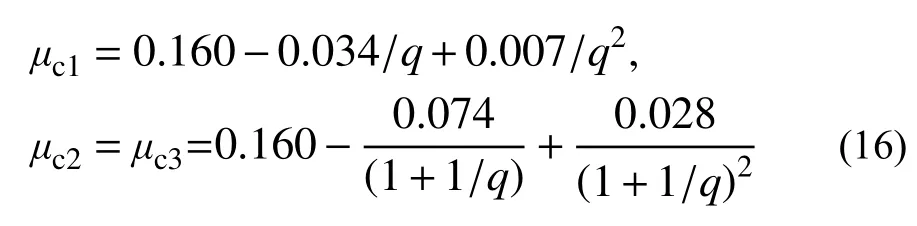
式中：μc1為軸向徐變泊松比；μc2為徑向徐變泊松比；μc3為環(huán)向徐變泊松比；q為鋼管對核心混凝土的緊箍力系數(shù)。根據(jù)鐘善桐[6]的工作，q的表達式為：

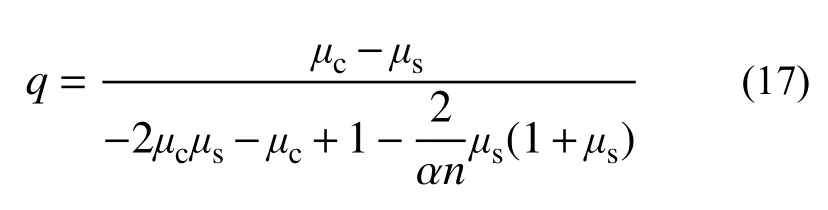
式中：μc為混凝土的泊松比；μs為鋼材的泊松比；α=As/Ac，As為外鋼管的截面積，Ac為核心混凝土的面積；n=Es/Ec，Es為外鋼管的彈性模量，Ec為核心混凝土的面積；μc由以下式給出：

三向應力狀態(tài)下，有 σx，σy，σz，τxy，τyz，τzx這6 個應力分量和 εx，εy，εz，γxy，γyz，γzx這6 個應變分量。寫成矩陣形式：

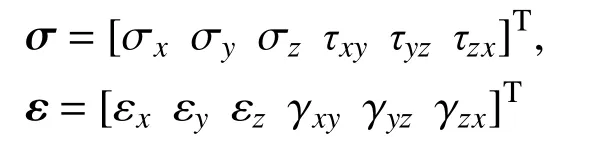
通過引入式(14)中的泊松比效應矩陣，根據(jù)粘彈性定律，三向應力狀態(tài)下的混凝土徐變應力-應變本構關系可由式(1)改寫為：

類似于第1 節(jié)單向應力狀態(tài)下混凝土徐變應力-應變本構關系的推導過程，同樣，可以從式(19)得到如下形式的三向應力狀態(tài)下的混凝土徐變應力-應變增量本構關系：

3 鋼管混凝土徐變有限元分析

將式(25)獲得的位移增量Δun+1代入式(20)，即可求得應力增量Δσn+1。

為實現(xiàn)上述這個數(shù)值計算目標，本文采用Fortran 語言二次開發(fā)Ansys 子程序Usermat。開發(fā)的子程序Usermat 功能可計算每一時步的三向應力狀態(tài)下混凝土徐變應變增量。在計算混凝土徐變應變增量的過程中，由于相鄰時刻的徐變應變增量間存在遞推關系(式(22))，因此，當前時刻Δtn+1混凝土徐變應變增量的計算需要調用上一時刻Δtn計算得到的ωn(參見式(21))。

4 算例驗證

為了驗證本文三向應力狀態(tài)下鋼管混凝土徐變計算模型的有效性和可靠性，本節(jié)基于ACI 徐變模型[27]，采用64 位Ansys 15.0+Vsiual Studio 2010+Inter Fortran Composer XE 2013 SP1 對Ansys 用戶材料子程序Usermat 進行二次開發(fā)，并嵌入到Ansys主程序中，實現(xiàn)長期荷載作用下素混凝土柱和鋼管混凝土柱的徐變計算。

4.1 算例1.既有鋼管混凝土結構徐變試驗

1) 2017 年Chen 等[10]進行了兩組共13 個鋼管混凝土柱徐變試驗。本文選取其中一根試件(CFT-0.3-CR)進行徐變計算驗證。該試件鋼管直徑D為140 mm，壁厚ts為2 mm，長度L為1050 mm。鋼管混凝土試件混凝土強度等級為C50，測得圓柱體混凝土強度fcm=62.3 MPa；試件的長期荷載作用軸向壓力比為0.30，即端面長期作用荷載為300 kN，加載時混凝土齡期為7 d。有限元計算模型及計算結果對比情況如圖2 所示，結果顯示本文計算方法得到的結果與原文試驗數(shù)據(jù)吻合良好。

圖2 文獻[10]鋼管混凝土短柱有限元模型及計算驗證Fig.2 Finite element model and calculation validations of concrete filled steel tube in [10]

2) 譚素杰、齊加連等[28]在1983 年-1984 年間進行了鋼管混凝土柱長期和短期徐變試驗。本文選取短期徐變試驗中試件號14 進行徐變計算驗證。該試件鋼管直徑D為108 mm，鋼管壁厚ts為1.97 mm，長度L為432 mm。鋼管混凝土試件核心混凝土立方體強度為33 MPa；鋼材屈服點fy=315 MPa，泊松比為0.28，彈性模量Es為220 GPa。試件的長期荷載作用軸向壓力比為0.51，即端面長期作用荷載為548 kN。計算結果與試驗結果對比情況如圖3 所示，本文計算結果與文獻[28]試驗數(shù)據(jù)在加載18 d 前吻合良好，之后相對試驗數(shù)據(jù)偏大，基本能夠準確描述該徐變試驗發(fā)展規(guī)律。

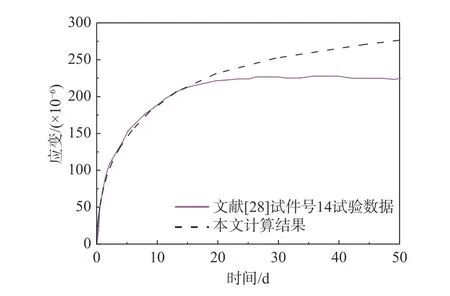
圖3 文獻[28]鋼管混凝土短柱計算驗證Fig.3 Calculation validations of concrete filled steel tube in [28]

4.2 算例2.鋼管混凝土徐變試驗

4.2.1 試件設計與加工

為驗證本文提出的鋼管混凝土軸壓短柱的徐變計算方法，進行試驗驗證。為避免試件過短使得端部效應影響顯著和試件過長而發(fā)生壓彎破壞，確定試件長徑比L/D=3。含鋼率設計為0.146。

試驗中設計2 個圓形素混凝土短柱，2 個圓形鋼管混凝土短柱，長度均為342 mm，混凝土強度等級均為C30，長期荷載作用軸向壓力比值為均0.3(實際加載值如表1 所示)，進行為期135 d 的長期試驗。鋼管名義截面尺寸為：114×3.75 mm2。在灌注混凝土之前，測得各鋼管實際厚度見表1。

表1 徐變試驗試件一覽表Table 1 List of creep test specimens

混凝土養(yǎng)護成型后，核心混凝土表面進行鑿毛處理，拌制環(huán)氧砂漿填平，待硬化后磨平以保證端板與混凝土能夠充分接觸，最后圍焊上端板。保證混凝土上表面與鋼管上表面齊平，從而保證鋼管與核心混凝土在加載和持荷階段共同受力。

4.2.2 材料力學性能

長期荷載作用下的鋼管混凝土試件的鋼管分別源于6 m 長的冷彎直縫鋼管。按照規(guī)范[29]制作3 個標準拉伸試件測得鋼材的屈服強度fy平均值為398 MPa，極限強度fu平均值為455 MPa。

澆筑鋼管混凝土試件同時，預留3 個邊長為150 mm 的混凝土立方體試塊，標準環(huán)境養(yǎng)護至構件軸壓試驗時測得混凝土抗壓強度fcu為44.04 MPa。

4.2.3 試驗加載與測試數(shù)據(jù)

參考文獻[11]試驗裝置，自行設計改進的自平衡加載裝置(圖4 所示)。試驗加載及后期持荷過程中，采用千斤頂配合反力架進行預加載并通過擰緊螺栓實現(xiàn)最終加載。為保證持荷穩(wěn)定，長期持荷過程中需對試件進行補載。實際試驗過程中，當NL降低2%以上時，進行補載，補載頻率保證試件荷載滿足規(guī)范[30]要求。

圖4 試驗裝置Fig.4 Test device

鋼管表面中部環(huán)向間隔90°對稱布置4 組電阻應變片測得鋼管應變；同時鋼管表面間隔180°布置2 組標距為200 mm 的不銹鋼測量端子，采用手持式應變儀測量鋼管應變；二者相互校核測量結果，發(fā)現(xiàn)所測得試件變形之差不超過5%，驗證本文使用的鋼管應變測試方法可靠。

4.2.4 試驗結果分析與算法驗證

徐變試驗室是在一定的溫度和濕度環(huán)境下進行的，試驗時室內溫度平均為24.04 ℃，濕度平均為59.22%，溫度和濕度變化情況如圖5 所示。圖6給出了素混凝土圓柱與鋼管混凝土軸壓短柱徐變試驗數(shù)據(jù)，兩組試驗均包含2 個平行試件。從圖中試驗數(shù)據(jù)可以發(fā)現(xiàn)，無論是單軸作用下的素混凝土圓柱還是核心混凝土受多軸應力作用下的鋼管混凝土短柱，構件的徐變數(shù)據(jù)均呈現(xiàn)為先快速增長再緩慢增長最終趨于平穩(wěn)的發(fā)展規(guī)律，與已有徐變試驗結果對比發(fā)現(xiàn)[10]，本文徐變試驗曲線能夠反映一般鋼管混凝土徐變發(fā)展規(guī)律；單軸荷載作用下，素混凝土徐變在持荷60 d 左右趨于穩(wěn)定；鋼管混凝土徐變在持荷30 d 左右趨于穩(wěn)定；鋼管混凝土徐變發(fā)展較素混凝土徐變較早趨于穩(wěn)定，并且徐變終值較素混凝土徐變小。

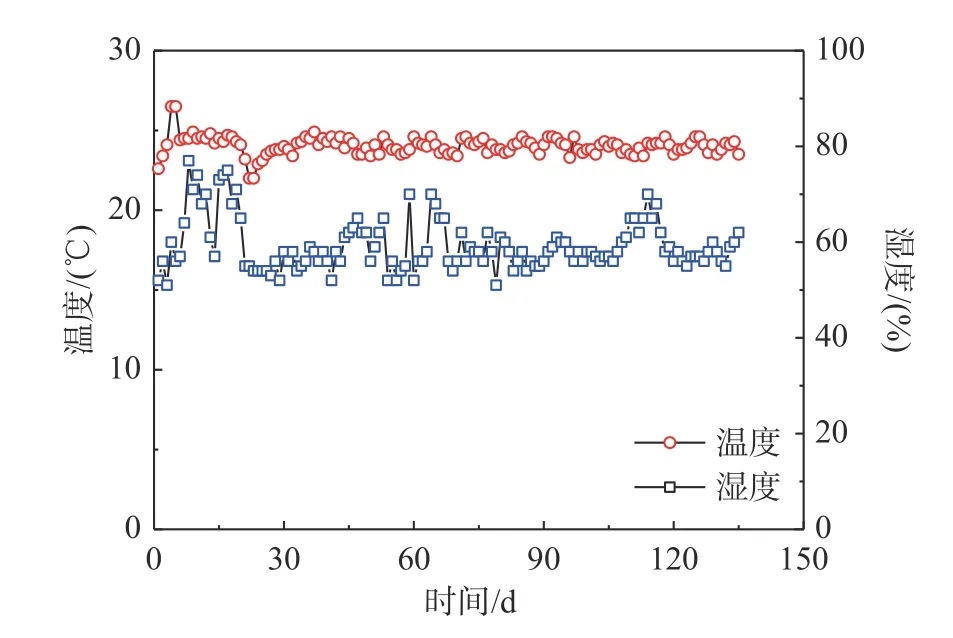
圖5 長期荷載試驗過程中溫度與濕度變化Fig.5 Variation of temperature and humidity measured during long-term test

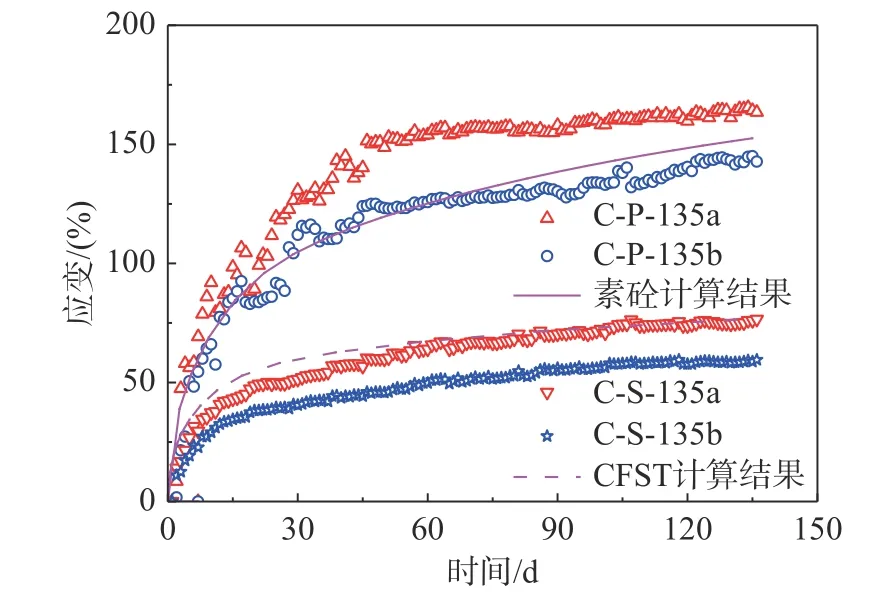
圖6 試驗結果與計算驗證Fig.6 Test results and calculation verification

從對比素混凝土徐變數(shù)據(jù)與鋼管混凝土徐變數(shù)據(jù)可以發(fā)現(xiàn)，相同條件下，鋼管混凝土徐變較素混凝土徐變小很多。其原因主要由于鋼管混凝土徐變過程發(fā)生應力重分布使作用力從徐變柔度更大的核心混凝土向蠕變應變率更小的外包鋼管轉移，外包鋼管對構件徐變具有抑制作用；密閉鋼管內核心混凝土無法與外界發(fā)生水分交換，故幾乎不發(fā)生干燥收縮和干燥徐變；另外，三向應力狀態(tài)對核心混凝土徐變度有影響，主要表現(xiàn)為緊箍力引起的橫向徐變泊松效應使核心混凝土徐變比素混凝土徐變要小。

圖5 給出本文試驗數(shù)據(jù)與計算結果對比情況，結果發(fā)現(xiàn)，素混凝土圓柱與鋼管混凝土軸壓短柱試驗數(shù)據(jù)與本文采用的率型徐變計算方法得到的計算結果均吻合良好，驗證了本文方法的適用性。

5 結論

本文從粘彈性力學角度出發(fā)，通過引入徐變泊松比效應和Kelvin 元件鏈，導出三向應力狀態(tài)下鋼管混凝土徐變計算模型。通過兩個已有鋼管混凝土徐變試驗及本文設計試驗，驗證了本文鋼管混凝土徐變計算模型，不僅可行，而且有效和可靠。

本文提出的三向應力狀態(tài)下混凝土徐變模型可以完善或彌補現(xiàn)有通用商業(yè)有限元軟件中混凝土徐變計算模型的不足，應用范圍更廣。