型鋼混凝土異形柱基于損傷的恢復(fù)力模型研究
劉祖強(qiáng),杜振宇,薛建陽,周超鋒
(1.西安建筑科技大學(xué)土木工程學(xué)院,陜西,西安 710055;2.西安建筑科技大學(xué)結(jié)構(gòu)工程與抗震教育部重點(diǎn)實(shí)驗(yàn)室,陜西,西安 710055;3.東南大學(xué)土木工程學(xué)院,南京 210096)
型鋼混凝土(SRC)異形柱的柱肢與填充墻等厚,柱棱在室內(nèi)不凸出,建筑觀瞻好,房間使用面積大,便于家具布置和室內(nèi)裝修。近年來,國(guó)內(nèi)外學(xué)者對(duì)SRC 異形柱的受力性能[1-6]進(jìn)行了系列研究,結(jié)果表明,該類構(gòu)件的承載能力高、抗震性能好。鑒于在建筑使用功能和受力性能方面的優(yōu)越性,SRC 異形柱結(jié)構(gòu)深受業(yè)主和房地產(chǎn)開發(fā)商的青睞[7]。
恢復(fù)力模型能夠反映地震作用下結(jié)構(gòu)或構(gòu)件強(qiáng)度、剛度等性能的退化,是實(shí)現(xiàn)結(jié)構(gòu)高效非線性地震反應(yīng)分析的重要基礎(chǔ)[8]。目前,部分學(xué)者針對(duì)不同形式的SRC 柱提出了恢復(fù)力模型。周穎等[9]建立了能夠反映強(qiáng)度和剛度退化及滑移等特征的空腹式SRC 柱恢復(fù)力模型;劉陽等[10]建立了能夠考慮核心型鋼配鋼率和軸壓比對(duì)滯回特性影響的核心SRC 柱恢復(fù)力模型;殷小溦等[11]考慮尺寸效應(yīng),分別建立了配鋼率低于10%和介于10%~20%的內(nèi)置十字形帶翼緣型鋼的SRC 柱恢復(fù)力模型;王斌等[12]引入基于損傷的循環(huán)退化指數(shù),建立了型鋼高強(qiáng)高性能混凝土柱的恢復(fù)力模型;薛建陽等[13]建立了型鋼再生混凝土柱的“定點(diǎn)指向”三折線恢復(fù)力模型。SRC 異形柱作為一種新型結(jié)構(gòu)柱,對(duì)其恢復(fù)力模型的研究較少,劉義等[14]建立了雙線型及退化三線型恢復(fù)力模型,但其形式相對(duì)簡(jiǎn)化,特征參數(shù)計(jì)算方法有待完善。
基于此,本文根據(jù)SRC 異形柱低周反復(fù)加載試驗(yàn)結(jié)果,研究了構(gòu)件的滯回特性,并采用理論推導(dǎo)和數(shù)據(jù)擬合相結(jié)合的方法,考慮截面形式、軸壓比和配鋼率的影響,建立了SRC 異形柱基于損傷的恢復(fù)力模型。
1 試驗(yàn)概況
共設(shè)計(jì)16 個(gè)實(shí)腹式配鋼的SRC 異形柱試件,包括10 個(gè)T 形柱(5 個(gè)沿腹板加載,5 個(gè)沿翼緣加載)、3 個(gè)十形柱和3 個(gè)L 形柱。試件的縮尺比為1∶2,剪跨比為2.5,具體設(shè)計(jì)參數(shù)如表1 所示。試件的立面如圖1 所示,截面配鋼如圖2 所示。試件所采用的混凝土、鋼板及鋼筋的物理力學(xué)性能詳見文獻(xiàn)[15 -17]。

圖1 試件的立面圖Fig.1 Elevation of specimen
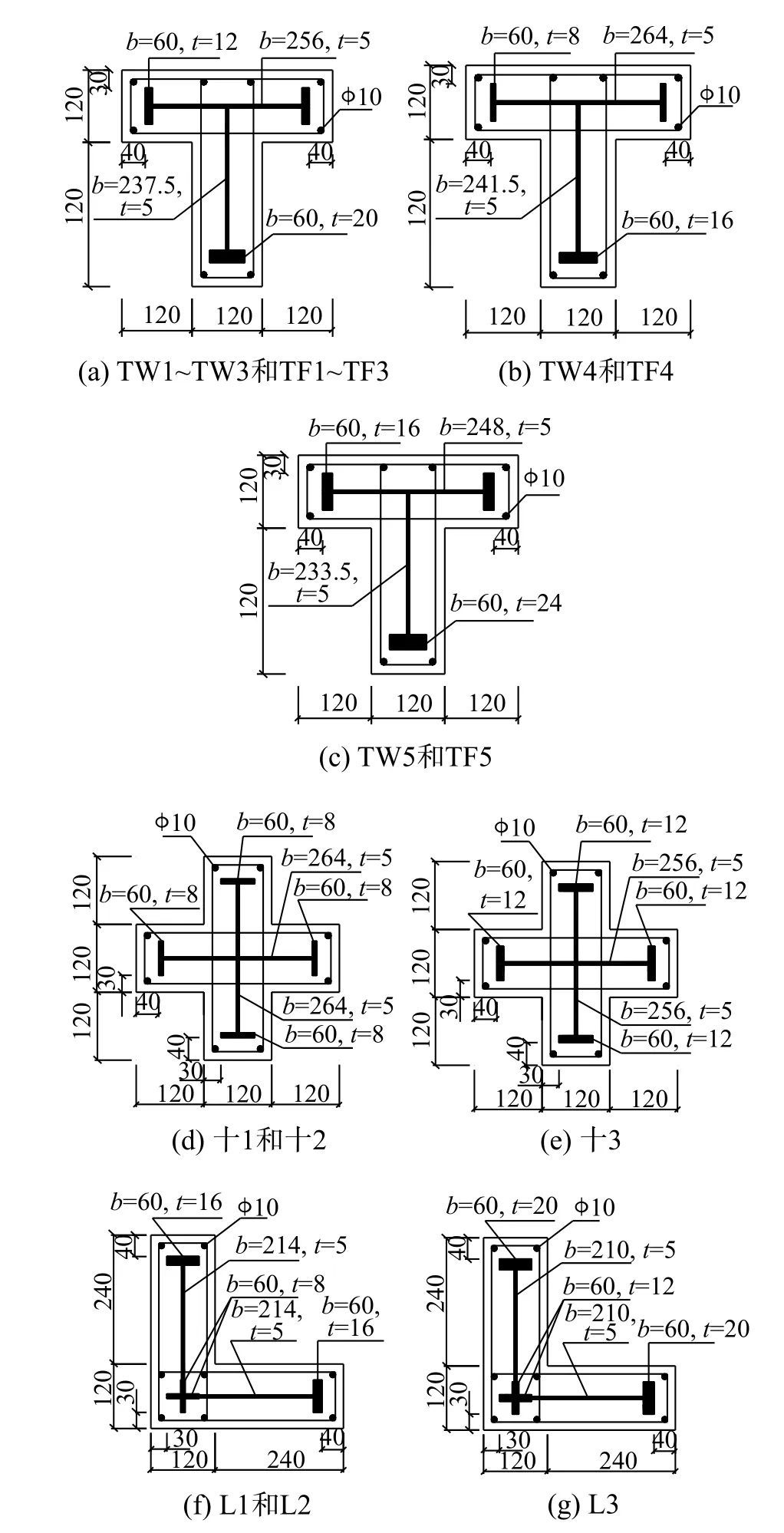
圖2 截面配鋼Fig.2 Layout of steel
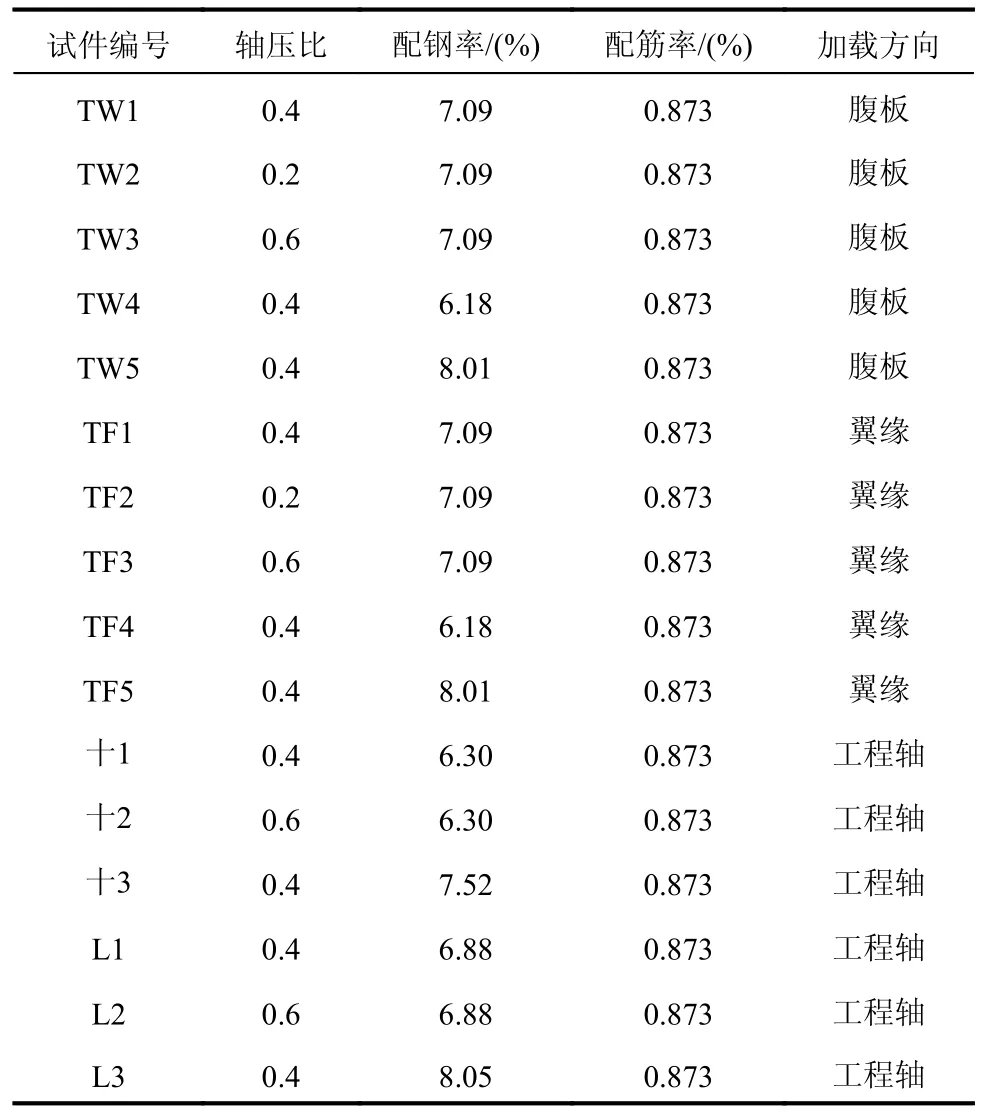
表1 試件設(shè)計(jì)參數(shù)Table 1 Design parameters of specimens
試驗(yàn)采用建研式加載裝置,首先利用液壓千斤頂與穩(wěn)壓設(shè)備在柱頂施加恒定豎向荷載,然后施加低周反復(fù)荷載。水平加載采用荷載與位移混合控制,荷載下降到峰值荷載的85%以下時(shí)停止加載。
2 型鋼混凝土異形柱滯回特性分析
試驗(yàn)得到試件的滯回曲線如圖3 所示,其中P、Δ分別代表柱頂?shù)乃胶奢d和位移。由圖3可知:
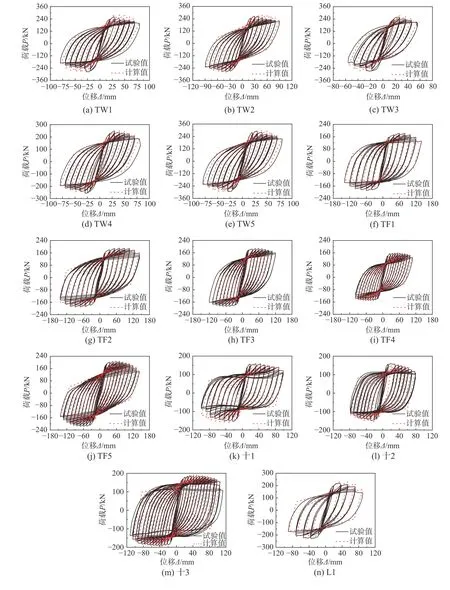
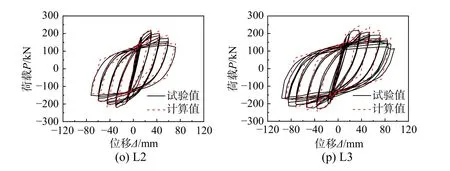
圖3 計(jì)算滯回曲線與試驗(yàn)結(jié)果對(duì)比Fig.3 The comparisons of computational hysteretic curves and testing hysteretic curves
1)所有試件的滯回曲線基本繞原點(diǎn)對(duì)稱,且呈飽滿的梭形,表明SRC 異形柱具有良好的耗能能力。
2)加載初期,試件處于彈性工作階段,加載路徑與卸載路徑基本重合;隨著荷載增大,試件剛度開始降低,滯回環(huán)面積不再為0,并逐漸向位移軸傾斜,表明試件已進(jìn)入到彈塑性工作階段。試件屈服后,不同位移幅值下的滯回環(huán)會(huì)在正、反向匯交于2 點(diǎn)。究其原因是由于實(shí)腹式SRC 異形柱的滯回路徑主要由上、下柱端腹板區(qū)域型鋼交替控制,試件在進(jìn)入初始損傷狀態(tài)后(即柱端腹板區(qū)域混凝土開裂且裂縫不斷發(fā)展,局部鋼材產(chǎn)生塑性變形),每當(dāng)復(fù)位并繼續(xù)反向加載時(shí),腹板區(qū)混凝土裂縫逐漸閉合(受壓區(qū)混凝土開始發(fā)揮作用),控制構(gòu)件滯回路徑的關(guān)鍵損傷區(qū)域便轉(zhuǎn)移到另一柱端的腹板受拉區(qū),故兩個(gè)匯交點(diǎn)不僅代表兩柱端腹板區(qū)域初步進(jìn)入損傷,同時(shí)每次通過這兩點(diǎn)也意味著控制構(gòu)件滯回路徑的關(guān)鍵損傷區(qū)域發(fā)生轉(zhuǎn)移交替。
3)峰值荷載后,試件的卸載剛度與再加載剛度明顯退化,且隨著荷載循環(huán)次數(shù)增加,試件內(nèi)部型鋼產(chǎn)生包辛格效應(yīng),控制構(gòu)件滯回路徑的腹板受拉區(qū)型鋼的拉伸屈服強(qiáng)度逐漸提高。
4)加載后期,混凝土大面積剝落,滯回路徑開始由更容易發(fā)生失穩(wěn)的柱端腹板受壓區(qū)型鋼控制,此時(shí)滯回曲線開始偏離匯交點(diǎn),標(biāo)志著構(gòu)件即將發(fā)生破壞。
3 基于損傷的恢復(fù)力模型的建立
恢復(fù)力模型是進(jìn)行結(jié)構(gòu)非線性地震反應(yīng)分析時(shí)降低計(jì)算成本與計(jì)算誤差的重要手段。它由骨架曲線與滯回規(guī)則兩部分組成,前者用以確定恢復(fù)力模型的主要特征點(diǎn),后者則用來高度體現(xiàn)結(jié)構(gòu)及構(gòu)件在循環(huán)荷載作用下的非線性力學(xué)性能。
3.1 骨架曲線
SRC 異形柱的骨架曲線可分為彈性段、強(qiáng)化段及下降段3 個(gè)主要階段。以往型鋼混凝土構(gòu)件的骨架曲線模型通常采用理想三折線,特征點(diǎn)多采用基于試驗(yàn)數(shù)據(jù)回歸擬合的經(jīng)驗(yàn)法來確定。該類骨架曲線模型由于過度簡(jiǎn)化,不僅其線性下降段無法準(zhǔn)確反映構(gòu)件在峰值點(diǎn)后的強(qiáng)度及剛度退化規(guī)律,降低計(jì)算精度,而且應(yīng)用范圍比較局限。因此,本文提出了一種彈性段-強(qiáng)化段為雙折線、下降段為指數(shù)函數(shù)曲線的骨架曲線模型,如圖4 所示,其特征點(diǎn)采用理論推導(dǎo)與經(jīng)驗(yàn)法相結(jié)合的方法進(jìn)行確定。
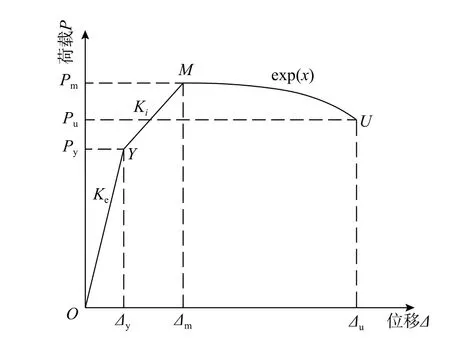
圖4 骨架曲線模型Fig.4 Skeleton model
1)彈性剛度Ke
Ke定義為屈服荷載與屈服位移的比值。為計(jì)算Ke,給出以下基本假定:
a)只考慮構(gòu)件的軸向變形與彎曲變形,不考慮構(gòu)件的剪切變形。
b)平截面假定,即垂直于構(gòu)件軸線的各平截面在變形后仍為平面且垂直于構(gòu)件軸線。
c)箍筋對(duì)混凝土的約束作用主要體現(xiàn)在骨架曲線下降段,不考慮配箍率對(duì)彈性剛度的影響。
d)不考慮混凝土的抗拉強(qiáng)度,以及受拉區(qū)混凝土對(duì)構(gòu)件抗側(cè)剛度的貢獻(xiàn)。
基于上述基本假定,并參照結(jié)構(gòu)力學(xué)形常數(shù)表現(xiàn),得到Ke的計(jì)算表達(dá)式如式(1)所示:
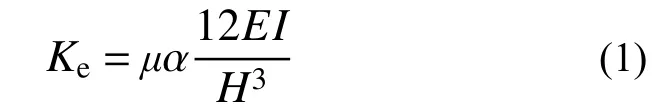
式中:EI為構(gòu)件截面初始抗彎剛度,可按式(2)計(jì)算;μ為軸壓附加抗側(cè)剛度系數(shù);α 為剛度退化系數(shù),用以考慮構(gòu)件從初始加載到屈服前由于損傷發(fā)展及粘結(jié)滑移造成的剛度退化,根據(jù)試驗(yàn)數(shù)據(jù)擬合,L 形柱、T 形柱(包括沿翼緣加載和沿腹板加載)和十形柱的α 值可分別取0.4、0.45 和0.5;H為柱凈高。
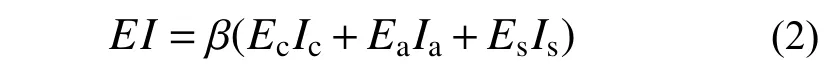
式中:β 為初始抗彎剛度修正系數(shù),用來修正計(jì)算時(shí)所采用一系列假定及邊界條件與構(gòu)件實(shí)際受力情況差異所造成的計(jì)算誤差,根據(jù)試驗(yàn)數(shù)據(jù)擬合,L 形柱、T 形柱(包括沿翼緣加載和沿腹板加載)和十形柱的β 值可分別取0.45、0.45 和0.6;Ec、Ea、Es分別為混凝土、型鋼、縱筋的彈性模量,Ic、Ia、Is分別為受壓區(qū)混凝土、全截面型鋼、全截面縱筋對(duì)中和軸的截面慣性矩。值得注意的是,L 形柱和沿腹板加載的T 形柱,其最不利受力狀態(tài)為腹板受壓翼緣受拉,計(jì)算時(shí)須以腹板作為受壓區(qū)進(jìn)行計(jì)算,沿翼緣加載的T 形柱和十形柱,其最不利受力狀態(tài)為翼緣一側(cè)受壓、另一側(cè)受拉,計(jì)算時(shí)須以翼緣的一側(cè)作為受壓區(qū)進(jìn)行計(jì)算。
確定中和軸位置時(shí)不僅考慮構(gòu)件截面幾何尺寸,還同時(shí)考慮不同材料的彈性模量所占權(quán)重,并且忽略受拉區(qū)混凝土對(duì)截面抗彎剛度的貢獻(xiàn)。中和軸的位置可按式(3)確定:
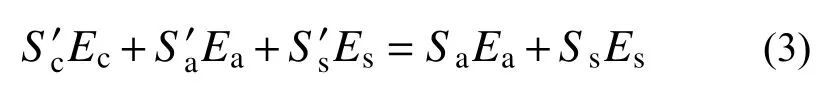
文獻(xiàn)[18]研究表明,軸向壓力對(duì)混凝土柱抗側(cè)剛度有較為明顯地影響,具體表現(xiàn)為兩方面:其一,側(cè)向位移較大時(shí),軸向壓力會(huì)因二階效應(yīng)降低柱的抗側(cè)剛度;其二,軸向壓力延緩了受拉區(qū)混凝土裂縫開展并增大了混凝土約束力,從而提高了柱的抗側(cè)剛度。本文在計(jì)算彈性剛度時(shí),由于側(cè)向位移較小,故只考慮軸向壓力對(duì)抗側(cè)剛度的有利影響,引入軸壓附加抗側(cè)剛度系數(shù)μ,可按式(4)確定:

式中,EIN為施加軸向壓力后因中性軸位置移動(dòng)而重新計(jì)算得到的截面初始抗彎剛度,以T 形柱(圖5)為例來說明EIN的計(jì)算方法。根據(jù)彈性力學(xué)計(jì)算方法聯(lián)立平衡方程、幾何方程及物理方程計(jì)算出構(gòu)件在純彎狀態(tài)下的全截面變形狀態(tài)(最大壓應(yīng)變?chǔ)與M及最大拉應(yīng)變?chǔ)舤M),然后,在軸心受壓狀態(tài)下將壓力以全截面均布荷載的方式施加在柱截面上,得到全截面壓應(yīng)變?chǔ)臢,進(jìn)行疊加,此時(shí)構(gòu)件截面受壓區(qū)高度也會(huì)從x1增加到x2,從而,將x2代入到式(2)計(jì)算出EIN。在計(jì)算純彎狀態(tài)下截面變形時(shí)不考慮受拉區(qū)混凝土的作用,但在計(jì)算εN時(shí)需考慮全截面混凝土的作用。
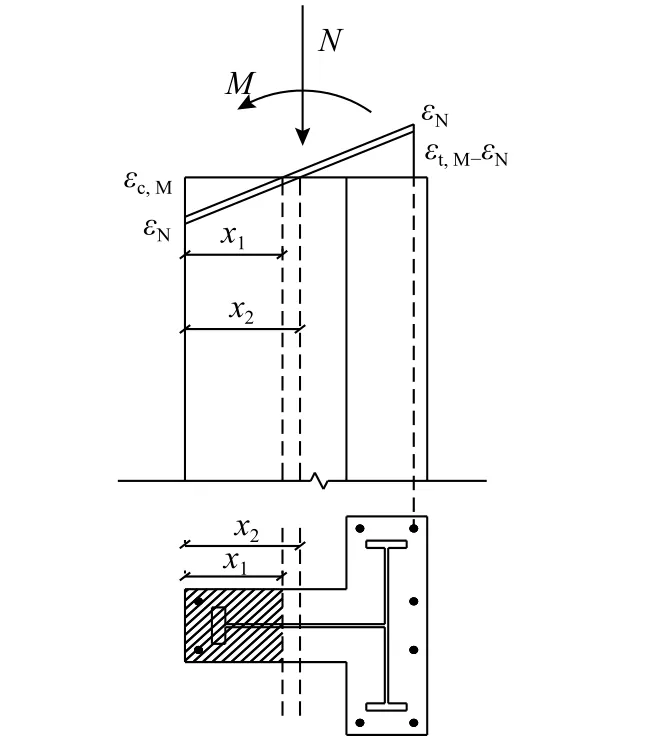
圖5 μ值的計(jì)算示意Fig.5 Schematic diagram for calculation of μ
2)屈服荷載Py
因彈性階段構(gòu)件側(cè)移較小,計(jì)算時(shí)忽略二階效應(yīng)所產(chǎn)生的附加彎矩,Py可按式(5)確定:

式中:H為柱凈高;My為構(gòu)件截面的屈服彎矩。
在確定My時(shí),根據(jù)前述基本假定,首先,利用式(3)并考慮軸壓影響確定構(gòu)件截面的中和軸位置,然后,將材料力學(xué)性能參數(shù)代入進(jìn)行積分計(jì)算,其中混凝土采用軸心抗壓強(qiáng)度,縱筋和型鋼采用屈服強(qiáng)度。
3)屈服位移Δy
Δy為Py與Ke的比值,可按式(6)進(jìn)行計(jì)算:

4)峰值荷載Pm和峰值位移Δm
對(duì)于型鋼混凝土異形柱構(gòu)件,影響其峰值點(diǎn)的因素眾多,如剪跨比、柱肢長(zhǎng)厚比、配筋率、配鋼率、配箍特征值、軸壓比、縮尺效應(yīng)、鋼與混凝土的粘結(jié)滑移特征及截面形式等。本文在計(jì)算時(shí)只考慮軸壓比、配鋼率和截面形式對(duì)峰值點(diǎn)位置的影響,原因?yàn)椋?/p>
a)異形柱多用于住宅建筑,柱肢與墻體等厚,柱高一般為3 m 左右,其剪跨比與柱肢長(zhǎng)厚比不會(huì)有太大變化。本次試驗(yàn)設(shè)計(jì)剪跨比及柱肢長(zhǎng)厚比皆為工程常用取值。
b)不同配筋率、配箍特征值和鋼與混凝土粘結(jié)滑移特征對(duì)計(jì)算結(jié)果的影響相對(duì)較小,故不加以考慮。
c)本次試驗(yàn)試件縮尺比例較大,不考慮縮尺效應(yīng)所帶來的影響。
故在考慮二階矩效應(yīng)基礎(chǔ)上,Pm與Δm可按平衡方程及物理方程所組成的方程組(7)聯(lián)立求解:

式中:N為構(gòu)件的軸向壓力設(shè)計(jì)值;Mm為柱端的極限彎矩,計(jì)算方法同My,區(qū)別在于鋼筋和型鋼采用極限強(qiáng)度,且只考慮箍筋內(nèi)約束混凝土的作用,因?yàn)樵嚰谶_(dá)到峰值點(diǎn)時(shí)柱端腹板區(qū)域箍筋外保護(hù)層混凝土已基本剝落;Km表示柱加載至峰值點(diǎn)時(shí)與原點(diǎn)的割線剛度,按式(8)計(jì)算。該式考慮了不同配鋼率及軸壓比引起的柱從屈服點(diǎn)到峰值點(diǎn)之間剛度退化速率的不同。

式中,λ 為剛度退化系數(shù),根據(jù)試驗(yàn)結(jié)果擬合,按式(9)計(jì)算。

式中:n為軸壓比;ρ 為配鋼率。
5)極限荷載Pu
P取P的85%,如式(10)所示:

6)下降段曲線exp(x)
根據(jù)試驗(yàn)數(shù)據(jù)擬合,骨架曲線下降段取指數(shù)函數(shù),由Pm、Δm及系數(shù)A和B確定,如式(11)所示:
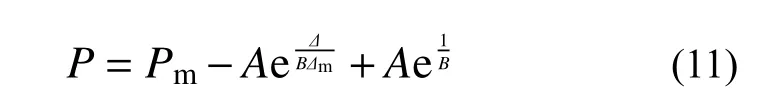
式中:系數(shù)A的取值取決于構(gòu)件的截面形式、軸壓比和配鋼率,A越大,表示下降段的強(qiáng)度衰減速度越快,根據(jù)試驗(yàn)數(shù)據(jù)擬合可得到其計(jì)算方法如式(12)所示;系數(shù)B代表了骨架曲線下降段在加載后期的強(qiáng)度退化速率,B值越小,表明構(gòu)件在大位移幅值下的強(qiáng)度退化越快,B的大小只與構(gòu)件截面形式相關(guān),根據(jù)試驗(yàn)結(jié)果,L 形柱、T 形柱(包括沿翼緣加載及沿腹板加載)與十形柱的B值可分別取0.5、0.5、1.0。
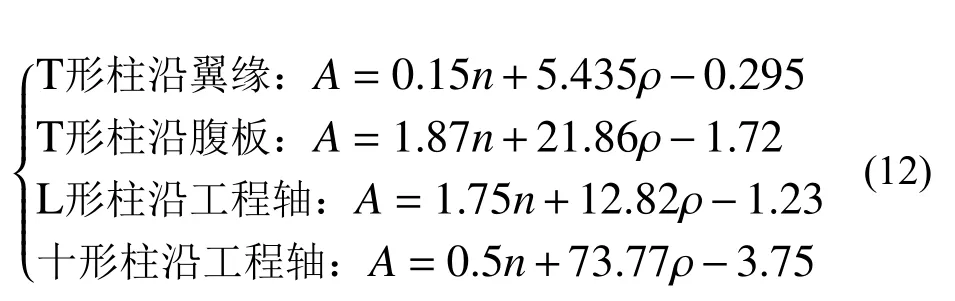
7)極限位移Δu
將式(11)等號(hào)左側(cè)替換為Pu,如式(13)所示,求得的Δ值即為Δu。
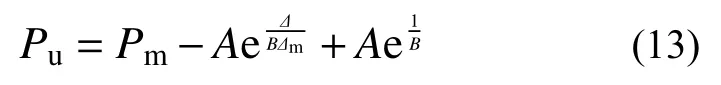
根據(jù)本文提出的骨架曲線模型確定方法,得到計(jì)算骨架曲線,并與試驗(yàn)骨架曲線進(jìn)行對(duì)比,如圖6 所示,骨架曲線特征點(diǎn)的計(jì)算值及其與試驗(yàn)值的對(duì)比如表2 所示,其中,Py、Δy、Pm、Δm、Pu和Δu的計(jì)算值與試驗(yàn)值比值的平均值分別為0.997、0.978、1.009、1.008、1.013 和1.066,方差分別 為0.002、0.018、0.002、0.033、0.002 和0.021,變異系數(shù)分別為0.045、0.137、0.044、0.180、0.044 和0.136。由圖6 及表2 可知,計(jì)算結(jié)果與試驗(yàn)結(jié)果吻合較好,表明采用本文方法確定型鋼混凝土異形柱的骨架曲線是合理可行的。
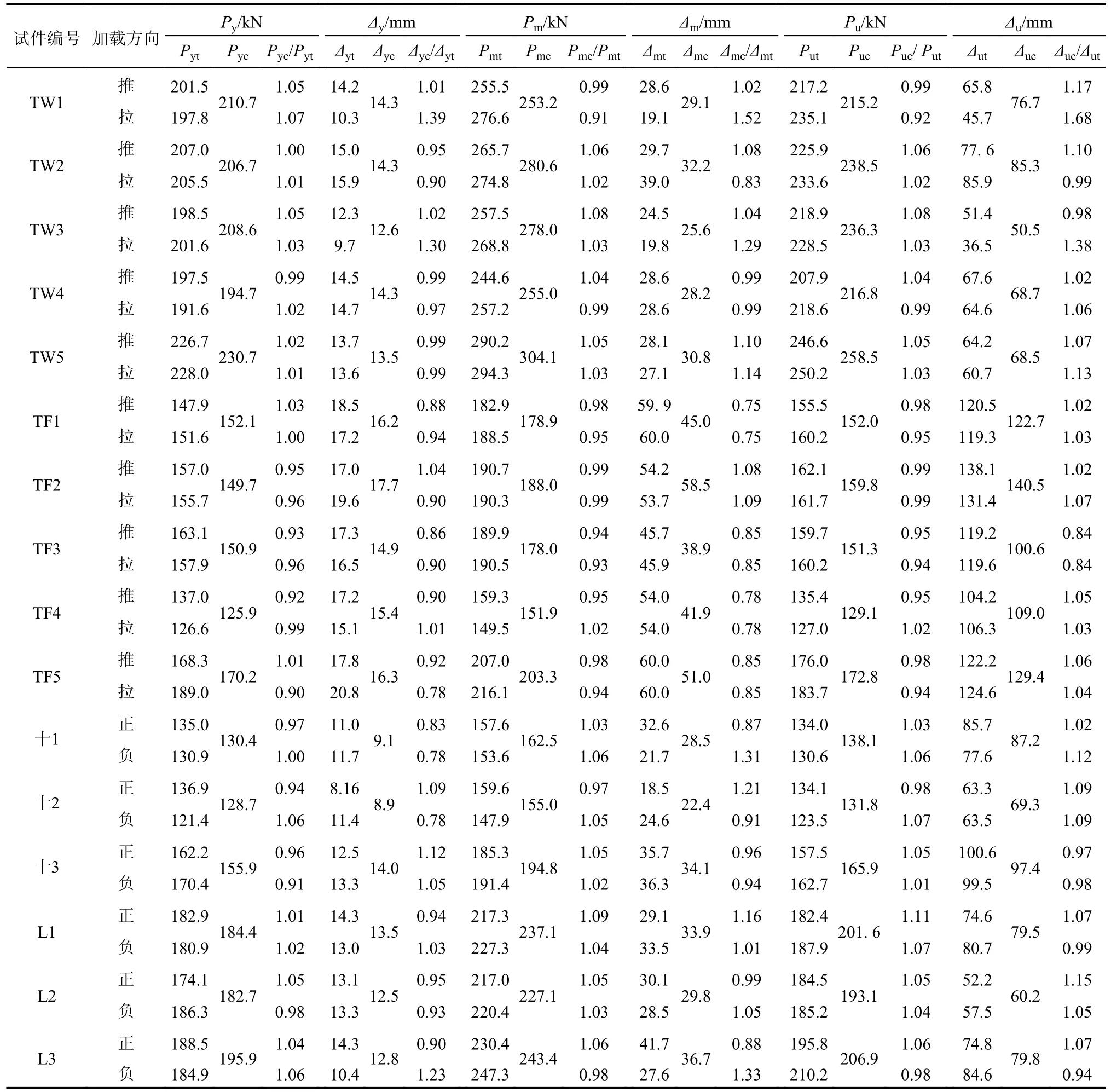
表2 骨架曲線特征點(diǎn)的計(jì)算值與試驗(yàn)值對(duì)比Table 2 Comparison of characteristic value of skeleton curves between calculation and test
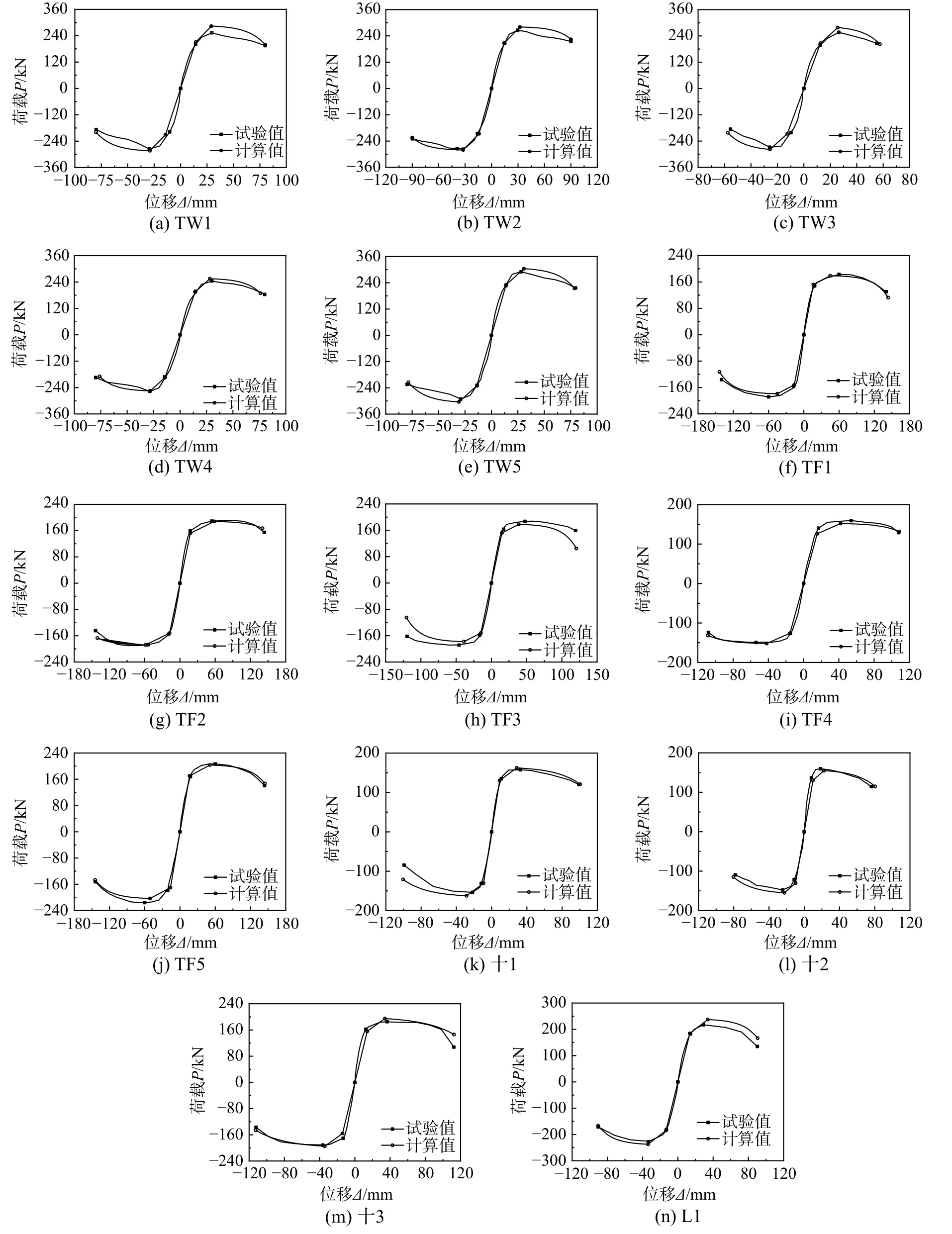

圖6 計(jì)算骨架曲線與試驗(yàn)骨架曲線對(duì)比Fig.6 Comparisons between computational skeleton curves and experimental skeleton curves
3.2 滯回規(guī)則
基于骨架曲線模型,考慮卸載剛度退化、強(qiáng)度衰減及包辛格效應(yīng)等因素的影響,建立SRC 異形柱基于損傷的恢復(fù)力模型如圖7 所示。
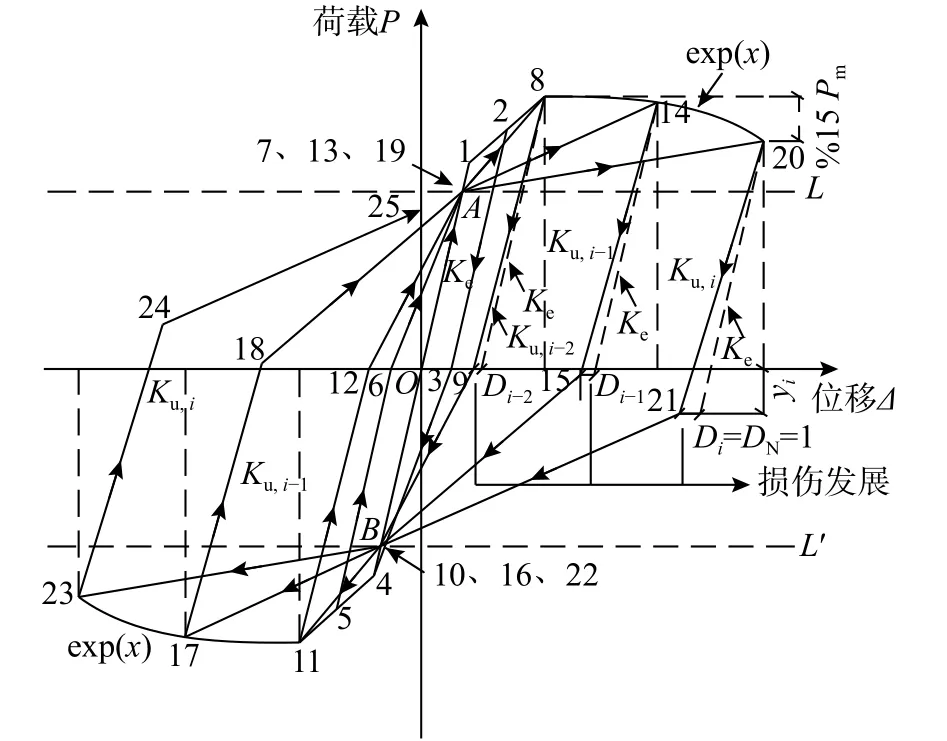
圖7 恢復(fù)力模型Fig.7 Restoring force model
1) 匯交點(diǎn)
根據(jù)滯回特性分析可知,試件屈服后,不同位移幅值下的滯回環(huán)分別在正、反向匯交于兩點(diǎn)。恢復(fù)力模型中的正、反向匯交點(diǎn)A、B為輔助線L、L′與彈性段直線1~4 的交點(diǎn),L、L′是與位移軸平行的兩條直線,其縱坐標(biāo)值主要隨截面形式及配鋼率的不同而變化,是與峰值荷載直接相關(guān)的參數(shù)變量。型鋼混凝土異形柱恢復(fù)力模型的匯交點(diǎn)縱坐標(biāo)值按式(14)確定,系數(shù)φ按表3 取值。
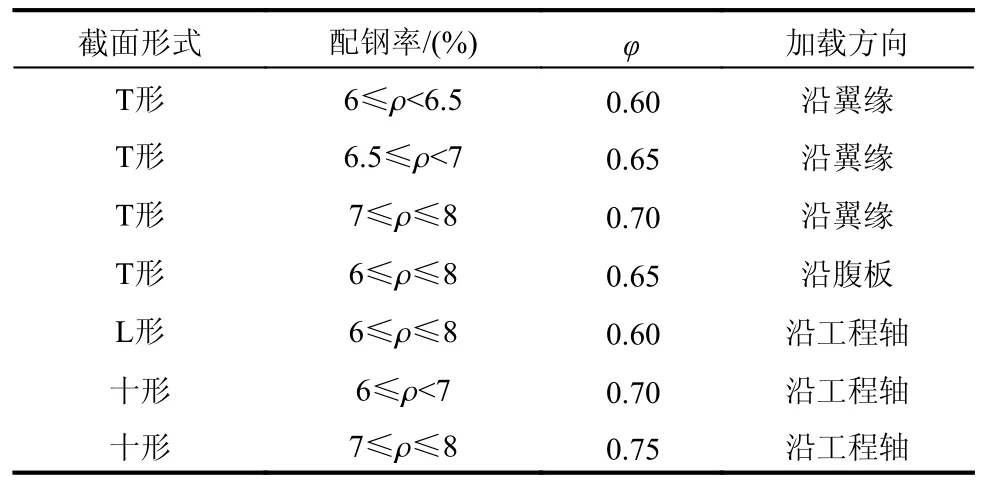
表3 參數(shù)φ 選取方法Table 3 The selection of parameter φ

2) 考慮損傷的卸載剛度退化
位移幅值的增加致使構(gòu)件損傷不斷累積,其卸載剛度也出現(xiàn)逐漸退化的現(xiàn)象[19]。本文采用了基于位移幅值的單參數(shù)損傷模型,將損傷指數(shù)Di引入到型鋼混凝土異形柱恢復(fù)力模型中,對(duì)構(gòu)件卸載剛度在加載歷程中的變化進(jìn)行定量描述。
從骨架曲線上的某一點(diǎn)卸載至與位移軸相交,則這兩點(diǎn)之間的割線剛度記為卸載剛度。由圖3 可以看出,試件在達(dá)到峰值荷載前,卸載剛度與彈性剛度相差不大,而已有研究表明[20],型鋼混凝土矩形柱在彈性階段和強(qiáng)化階段的卸載剛度未發(fā)生明顯退化,與彈性剛度基本相同。因此,本文恢復(fù)力模型中的卸載剛度在峰值點(diǎn)前與彈性剛度相同,在峰值點(diǎn)后考慮由損傷效應(yīng)引起的退化。
圖8 表示不同截面形式的型鋼混凝土異形柱在峰值點(diǎn)后損傷指數(shù)與位移幅值的關(guān)系,將其擬合得到的關(guān)系式如式(15)所示。
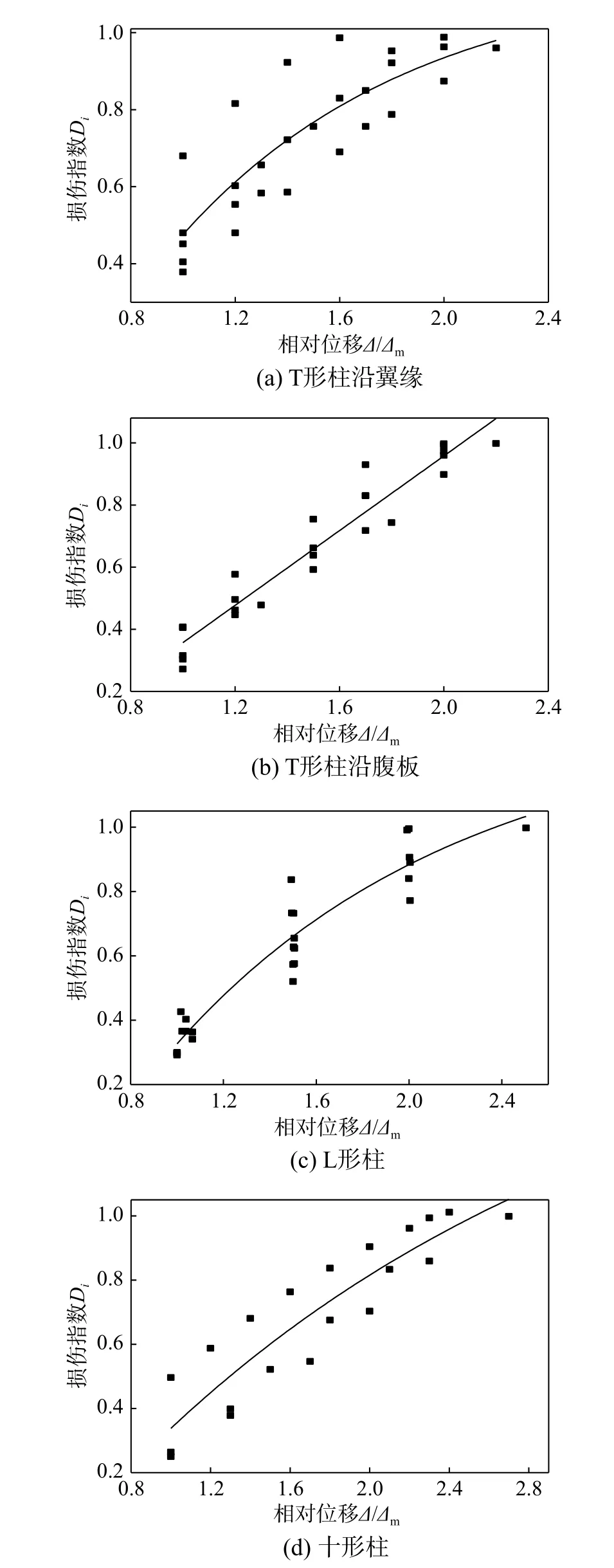
圖8 試件損傷指數(shù)與水平位移的擬合關(guān)系Fig.8 The fitting curve of damage index and horizontal displacement of specimen
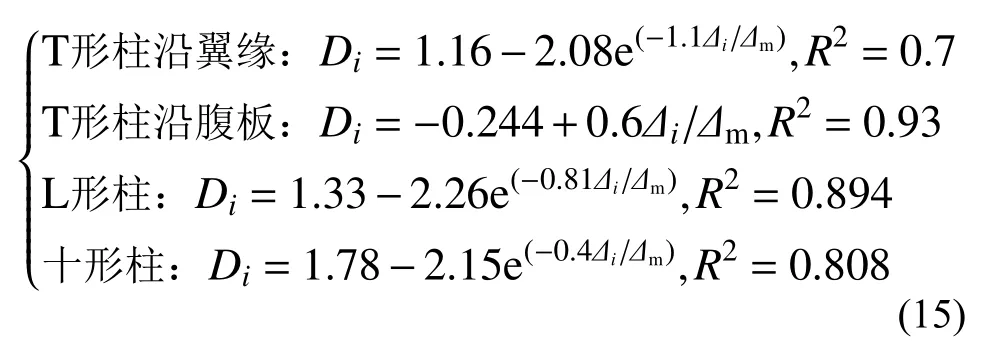
進(jìn)一步得到試件的卸載剛度與其損傷指數(shù)的關(guān)系如圖9 所示,并通過擬合得到恢復(fù)力模型中峰值點(diǎn)后卸載剛度的計(jì)算式,如式(16)所示。
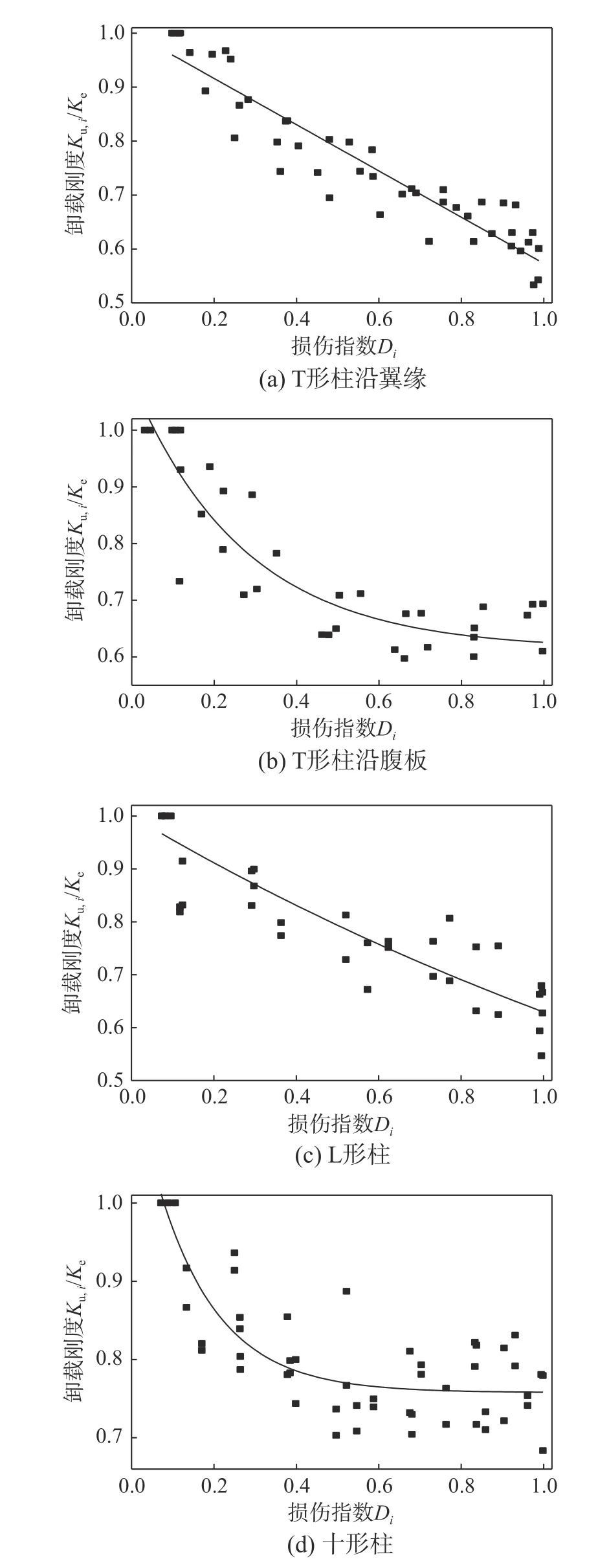
圖9 卸載剛度與損傷指數(shù)的擬合關(guān)系Fig.9 The fitting curve of unloading stiffness and damage index of specimen
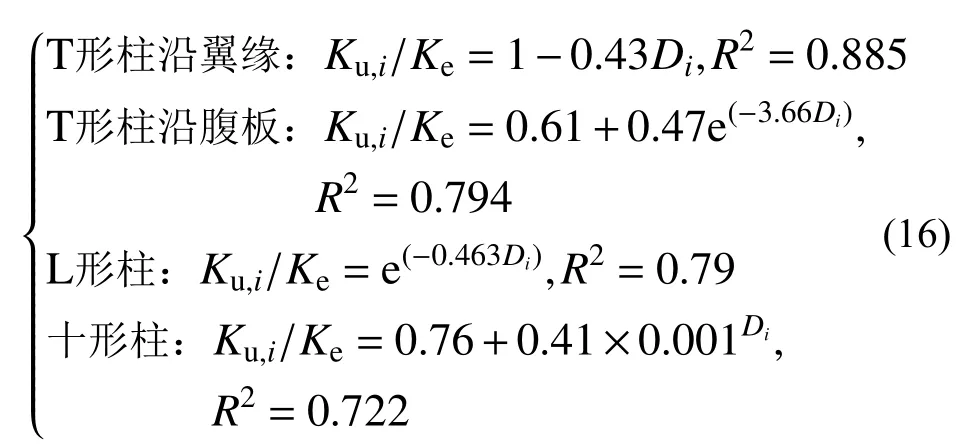
3) 強(qiáng)度衰減
SRC 異形柱強(qiáng)度衰減系數(shù)取γi=Pi/P,其中:P為某級(jí)控制位移幅值下的第1 次循環(huán)的荷載最大值;Pi為第i次循環(huán)的荷載最大值。由荷載-位移曲線可知,不同配鋼率及軸壓比的試件均展現(xiàn)出了良好的強(qiáng)度穩(wěn)定性,沒有出現(xiàn)較大的離散。根據(jù)試驗(yàn)結(jié)果,將SRC 異形柱每級(jí)加載循環(huán)下第2 循環(huán)的強(qiáng)度衰減系數(shù)γ2取為0.93,第3 循環(huán)的強(qiáng)度衰減系數(shù)γ3取為0.9,參考文獻(xiàn)[14],多次循環(huán)下強(qiáng)度衰減系數(shù)γn的臨界閾值取為0.85。
4) 反向加載轉(zhuǎn)折點(diǎn)
構(gòu)件在卸載后反向加載時(shí),曲線出現(xiàn)明顯轉(zhuǎn)折,此處稱為反向加載轉(zhuǎn)折點(diǎn),如圖7 中的點(diǎn)3、6、9、12、15、18、21 和24。在峰值點(diǎn)前,反向加載轉(zhuǎn)折點(diǎn)均交于位移橫軸,峰值點(diǎn)后,構(gòu)件內(nèi)部型鋼由于反復(fù)荷載作用產(chǎn)生了明顯的包辛格效應(yīng),反向加載轉(zhuǎn)折點(diǎn)沿卸載段發(fā)生了不同程度地延伸(如圖7 中yi段)。根據(jù)試驗(yàn)得到的荷載-位移曲線進(jìn)行擬合,型鋼混凝土異形柱恢復(fù)力模型反向加載轉(zhuǎn)折點(diǎn)的縱坐標(biāo)值可按式(17)確定。
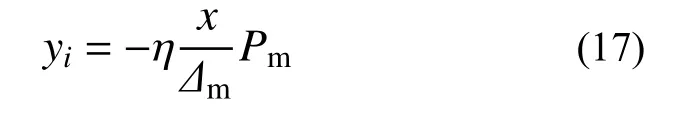
式中:x為第i次循環(huán)的柱頂水平位移幅值;η 為反向加載轉(zhuǎn)折點(diǎn)的強(qiáng)度增大系數(shù),L 形柱、沿腹板加載的T 形柱、沿翼緣加載的T 形柱和十形柱的η 值分別取0.09、0.1、0.12 和0.15。
基于上述分析,給出型鋼混凝土異形柱基于損傷的恢復(fù)力模型滯回規(guī)則如下:
構(gòu)件屈服前為彈性階段,加卸載路徑沿線段1~4 反復(fù)進(jìn)行,構(gòu)件不存在任何損傷。達(dá)到屈服荷載后,構(gòu)件進(jìn)入到強(qiáng)化階段,第1 加載循環(huán)在到達(dá)正向屈服點(diǎn)1 后,繼續(xù)沿強(qiáng)化段到達(dá)加載控制點(diǎn)2,然后卸載至反向加載點(diǎn)3,再反向加載直指負(fù)向屈服點(diǎn)4,隨后的負(fù)向加卸載路徑與正向相同。構(gòu)件在第2 加載循環(huán)時(shí)已產(chǎn)生損傷,加載路徑由點(diǎn)6 直接指向滯回曲線匯聚點(diǎn)A,然后到下一個(gè)加載控制點(diǎn)8。在峰值點(diǎn)前,任意位移幅值下的卸載剛度都等于彈性剛度Ke。峰值點(diǎn)后,滯回路徑規(guī)則并不發(fā)生變化,仍然通過匯交點(diǎn)A、B反復(fù)進(jìn)行;構(gòu)件強(qiáng)度進(jìn)入衰減階段,卸載剛度(按式(16)確定)發(fā)生退化;由于包辛格效應(yīng),反向加載轉(zhuǎn)折點(diǎn)對(duì)應(yīng)的強(qiáng)度不斷提高,其坐標(biāo)位置不再是卸載路徑與位移軸交點(diǎn),而是沿卸載路徑延伸至縱坐標(biāo)值為yi(按式(17)確定)處;同一級(jí)位移幅值下反復(fù)加載時(shí)通過調(diào)整滯回環(huán)峰值點(diǎn)縱坐標(biāo)來考慮循環(huán)次數(shù)所造成的強(qiáng)度衰減;骨架曲線下降段函數(shù)exp(x)只作為確定滯回環(huán)峰點(diǎn)的依據(jù),并不作為恢復(fù)力模型滯回路徑的一部分。
4 恢復(fù)力模型驗(yàn)證
根據(jù)本文提出的骨架曲線模型及滯回規(guī)則,得到試件的計(jì)算滯回曲線,并與試驗(yàn)滯回曲線進(jìn)行對(duì)比,如圖3 所示。由圖可知,試件的計(jì)算滯回曲線與試驗(yàn)滯回曲線吻合度較高,可準(zhǔn)確反映SRC 異形柱在不同軸壓比及配鋼率下各受力階段的強(qiáng)度、剛度變化規(guī)律及耗能能力。
值得注意的是,本文所提出骨架曲線模型和基于損傷的恢復(fù)力模型僅適用于實(shí)腹式配鋼的型鋼混凝土異形柱,且為剪跨比大于2 的壓彎構(gòu)件。對(duì)于受剪切變形影響較大的短柱,還須作進(jìn)一步研究。
5 結(jié)論
本文基于16 個(gè)SRC 異形柱的低周反復(fù)加載試驗(yàn),對(duì)于該類構(gòu)件的恢復(fù)力模型進(jìn)行研究,得到以下主要結(jié)論:
(1) SRC 異形柱荷載-位移滯回曲線基本呈梭形,抗震性能穩(wěn)定,耗能能力強(qiáng);構(gòu)件產(chǎn)生損傷后,不同控制位移幅值下的滯回環(huán)在正、反向匯交于兩點(diǎn);反復(fù)循環(huán)荷載作用下,構(gòu)件內(nèi)部型鋼將產(chǎn)生包辛格效應(yīng),在峰值點(diǎn)過后,各滯回環(huán)反向加載轉(zhuǎn)折點(diǎn)對(duì)應(yīng)的強(qiáng)度與位移幅值、循壞次數(shù)成正比。
(2)基于理論推導(dǎo)與試驗(yàn)數(shù)據(jù)擬合,提出了彈性段-強(qiáng)化段為雙折線、下降段為指數(shù)函數(shù)曲線的骨架曲線模型,該模型能高度擬合構(gòu)件在加載后期的強(qiáng)度與剛度退化特征,對(duì)于提高結(jié)構(gòu)非線性地震反應(yīng)分析時(shí)的模擬精度具有重要意義。
(3)考慮加載歷程對(duì)型鋼混凝土異形柱性能退化的影響,通過引入基于位移幅值的單參數(shù)損傷指數(shù),定量描述了構(gòu)件位移與損傷的關(guān)系,得到了卸載剛度退化規(guī)律。
(4)根據(jù)所提出的骨架曲線模型及滯回規(guī)則,以截面形式、配鋼率、軸壓比為主要變化參數(shù),建立了SRC 異形柱基于損傷的恢復(fù)力模型,該模型計(jì)算簡(jiǎn)便,精度高,適用于以彎曲變形為主的SRC 異形柱。

