基于通道特征選擇的加權響應目標跟蹤

劉佳榆，余 華，徐 舒

(武漢東湖學院電子信息工程學院，湖北 武漢 430200)

1 引言

視覺目標跟蹤是指在視頻序列中利用第一幀目標信息和后續幀中目標之間的關聯信息來獲得目標狀態和位置的一種計算機視覺技術。其被廣泛應用于視頻監控、行為分析、人機交互等諸多領域。

現有的目標跟蹤算法包括模板匹配、統計學習、粒子濾波、相關濾波、深度神經網絡等幾大類，其中相關濾波跟蹤算法由于在速度和精度上取得了較好的折中，所以受到了目標跟蹤領域研究者們的廣泛關注。Matthias Mueller等[1]提出上下文感知相關濾波算法，通過將全局環境上下信息集成到相關濾波器學習過程中使得濾波器能夠結合環境上下文信息對目標進行判別，極大的提高了跟蹤的精確度；Wang等[2]提出多線索相關濾波跟蹤算法，通過構建特征專家庫和最優特征評估準則的方法選擇最佳特征應用于特定幀進行目標跟蹤，實現具體到幀的最優特征選擇，使得應用于目標跟蹤的特征針對針對性進一步加強，取得了較好跟蹤效果；孫希延等[3]提出亞像素相關濾波跟蹤算法，該算法利用拋物線模型對離散的目標響應值近似擬合，然后引入泰勒級數對擬合后的連續二次曲線求解，使得目標跟蹤的定位精度達到亞像素級別；Huang等[4]提出學習畸變抑制的相關濾波器的無人機實時目標跟蹤算法，其通過引入正則化項的方式來抑制由引入的背景噪聲信息引起的相響應圖畸變，從而提高了算法在復雜背景下的跟蹤穩健性。

相關濾波類算法誕生初期，所采用表示目標的特征一般為CN特征、HOG特征等人工設計特征，隨著深度學習的疾速發展，研究人員發現深度卷積特征具備強大的特征表征能力，因此深度卷積特征被引入到相關濾波框架下進行目標跟蹤，提高算法的精確度與穩健性。但是，目前的相關濾波跟蹤算法在利用深度特征進行目標跟蹤的時候，多采用神經網絡最后一層特征進行跟蹤，忽略低層卷積特征包含的目標輪廓信息對目標定位的有利影響。與此同時深度卷積特征以多個通道維度對目標各屬性進行表征，可能存在通道特征冗余和特征不相關問題，這會導致算法復雜度過高和跟蹤精度受損。

因此，為了解決上述問題，本文首先通過在通道維度上定義一個通道正則化項來進行通道特征選擇以解決特征冗余和不相關問題，然后通過多層響應圖加權融合方式以綜合高層語義特征和低層輪廓信息來實現目標定位。

2 傳統相關濾波算法

本文算法以傳統相關濾波算法為基礎框架，因此需要對基礎算法框架進行概要介紹，傳統相關濾波跟蹤算法通過給定第一幀目標外觀信息訓練濾波器和利用后續幀目標信息進行濾波器更新以實現目標跟蹤，由于其速度快、穩健性良好等特點而具備較大應用價值。

相關濾波通過最小化估計目標狀態響應與期望目標狀態響應之間的誤差來實現濾波器的訓練，具體如式(1)所示

(1)

在跟蹤階段，除了第一幀學習到的濾波器可以直接在第二幀中用來跟蹤以外，其余幀需要需要結合前一幀濾波器對當前幀濾波器進行更新以提高跟蹤器的自適應性，具體如式(2)所示

(2)

式中，α∈[0，1]表示預定義更新率，ft表示第t幀訓練出的濾波器，其目的是將其用在第t+1幀中進行目標位置預測。

在第t+1幀中首先提取該幀中多通道特征，然后將相應通道濾波器與對應通道特征分別變換到頻域，并進行元素點乘獲得該通道頻域響應圖，最后將各通道頻域響應圖加和便可得到最終頻域響應圖，具體如式(3)所示

(3)

3 本文算法

本文算法主干分支框架如圖1所示：首先通過在ImageNet數據集[5]上預訓練的VGG-M[6]網絡提取各層深度特征，由于要考慮到各通道特征的分辨率差異，所以需要對提取特征進行隱式插值；然后由于各通道特征可能存在特征冗余和不相關問題，因此采用通道特征選擇機制對各通道特征進行選擇以降低特征冗余和不相關性，提高特征的表征性能；最后采取低層特征響應與高層特征響應加權融合方式提高算法的定位精度和判別能力。

圖1 主干分支框架圖

3.1 隱式插值模型

由于采樣點不同，而又需要將跟蹤問題變換到連續空間域求解，因此需要對特征進行插值，因此采用式(4)所示隱式插值方式進行特征連續性處理

(4)

式中，[0，T)?R表示特征圖的空間支持范圍，bd∈L2(T)，其表示希爾伯特空間中的插值函數，p∈[0，T)表示空間域中像素位置。

完成上述插值后，該卷積層響應置信度可定義為多個通道特征響應加和形式，具體如(5)式所示

(5)

式中，fd∈L2(T)表示第d個通道的濾波器，Sf(x)表示卷積層置信度。

經過空間插值操作可得訓練濾波器所用到的代價函數如(6)式所示

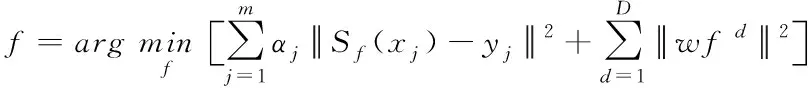
(6)

式中，yj∈L2(T)表示在希爾伯特空間中xj的標簽真值，αj表示每個訓練樣本的權重。

3.2 通道特征選擇

在式(5)中所使用的卷積特征為高維多通道特征，這樣的特征存在特征冗余和不相關性，因此會影響所訓練濾波器的性能，為了解決這一問題，本文引入文獻[7]中的稀疏組套索方法對特征進行選擇，其具體式如(7)式所示

(7)

式中，λ2為平衡參數，在(7)式中第二項即懲罰項其實是先對fd求l2范數，再求加和項的l1范數，這個是典型的l2，1組套索模型，用這種模型便可實現對通道的組特征選擇。

3.3 響應加權融合

在(7)式中雖然考慮到了通道特征冗余和不相關問題，但是卻沒有解決高層語義特征與低層結構特征的結合應用問題，因此所提算法采用文獻[8]中多層特征響應加權融合策略提高跟蹤的精度，則(5)式變為如下(8)式所示

(8)

式中，Dconv1表示第一層卷積特征的通道數，Dconv5表示第五層卷積特征的通道數，上下標a，b分別表示第a個通道和第b個通道。w1表示第一層卷積特征響應融合權重，w2表示第五層特征響應融合權重。

將(8)式代入(7)式可得所提算法最終跟蹤濾波器的最優目標函數

(9)

3.4 尺度估計

對于目標最佳尺度的選擇傳統相關濾波器一般采用尺度池策略進行估計，但是所提算法由于使用了深度特征進行目標跟蹤，如果繼續進行尺度池策略進行目標尺度估計會導致算法速度嚴重下降，因此所提算法采用文獻[ ]中的方法通過利用HOG特征訓練一個專用的尺度估計模型進行尺度估計，從而使得在尺度估計過程中算法速度不下降。

所提算法的尺度估計框架如圖2所示，分別訓練兩個相關濾波器模型，一個用于目標定位，一個用于目標尺度估計。目標定位階段由于考慮到定位準確度，所以采用上文提出的通道特征選擇和加權響應相結合訓練出的模型進行定位，目標尺度估計則利用HOG特征訓練出的傳統核相關濾波器(KCF)模型進行尺度估計，ADMM表示的是交替方向乘子法，其用于對(9)式和尺度估計模型進行參數優化求解。

圖2 尺度估計框架示意圖

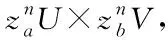
(10)

式中，通過比較各個尺度的下響應圖峰值大小，最大峰值的特征圖所對應的目標尺度為最佳尺度。

4 實驗分析

為分析算法的效果，通過采用表1所示的OTB2015數據集中9組測試視頻序列對所提算法進行性能測試，并與近幾年性能較為優秀的自適應空間正則化相關濾波算法(ASRCF)[9]、學習連續卷積算子跟蹤算法(CCOT)[10]、聯合群特征選擇和判別濾波算法(GFSDCF)[7]、對沖深度跟蹤算法(HDT)[11]、多任務相關粒子濾波跟蹤算法(MCPF)[12]等算法進行定量與定性分析以論證算法的有效性。

表1 9組視頻序列屬性

4.1 實驗配置與參數設置

本文所用實驗環境為Win10操作系統，實驗平臺為Matlab2020a，硬件配置CPU 12核3.8GHz Intel I7處理器，內存(RAM)為32G，顯卡為雙路RTX TITAN。通過經驗調優對算法參數進行了設定，平衡參數λ2=1.3，權重參數w1和w2分別設置為0.3和0.7。

4.2 定量分析

為了客觀分析所提算法CFSWR的效果，在實驗中通過測定所提算法的成功率和精確度以量化分析算法性能。通過實驗對比分析得到如圖3所示成功率圖和圖4所示精確度圖。

在圖3中可知所提算法成功率為0.929，成功率在6種算法中排名第一，相較于CCOT算法提升9.2%；在圖4中可知所提算法精確度為0.929，精確度在6種算法中也排名第一，相較于CCOT算法提升3.2%。根據成功率和精確度的定量比較可知所提算法CFSWR的準確性和魯棒性良好。

圖3 成功率圖

圖4 精確度圖

4.3 定性分析

為了更直觀分析本文所提算法效果，實驗中通過分別記錄算法在背景雜亂、運動模糊、尺度變化等三種情況下的跟蹤結果框圖以進行定性分析。

4.3.1 背景雜亂場景算法性能分析

圖5所示為背景雜亂情況下各算法的跟蹤效果，在carDark視頻序列中由于夜間行車，周圍燈光干擾和相似目標導致跟蹤環境背景比較雜亂，對跟蹤目標汽車產生了較大挑戰，在第229幀中HDT算法雖然應用了多層卷積特征，但是其沒有考慮到特征冗余問題，所以其產生了跟蹤漂移現象，在第280幀中MCPF也產生了大幅度跟蹤漂移，這是因為MCPF算法雖然考慮到多尺度和多層特征相關性，但其沒有解決特征冗余問題，所以導致算法在較為復雜環境下產生跟蹤漂移。

在soccer序列中由于田徑慶祝時所使用的彩花、人體運動、服裝相似等情況導致背景非常復雜，在shaking序列場景為搖滾音樂場景，由于夜間強光閃爍和搖滾歌手的快速運動等導致所拍攝場景比較混亂，因此在soccer序列第177幀、353幀和shaking序列第193幀、338幀時不僅HDT、MCPF出現跟蹤漂移，而且CCOT算法也出現了小幅度跟蹤漂移，這是因為CCOT算法考慮到了多層卷積特征分辨率差異問題，對其進行了空間變換插值處理，所以在背景雜亂場景下跟蹤效果較好，但由于沒有考慮到特征不相關性和冗余問題，所以仍會出現產生跟蹤漂移問題。然而，由于CFSWR不僅考慮到多層卷積特征融合問題和特征分辨率不一致問題，還考慮到特征相關性和冗余性，因此在圖5所示背景雜亂的三個序列中跟蹤效果較好。

圖5 背景雜亂

4.3.2 運動模糊場景算法性能分析

圖6所示為運動模糊情況下各算法的跟蹤效果，在ironman序列中鋼鐵俠運動速度極快且背景較為復雜，導致圖片產生運動模糊效果，在這種環境下跟蹤目標難度極大。在ironman序列第120幀時只有本文所提算法CFSWR和CCOT算法能夠準確跟蹤目標，這是因為相交于其它算法這兩個算法使用了都使用了多層卷積特征且考慮了各層特征分辨率不一致問題，所以最后使用的特征表征能力較強，能在運動模糊場景下較好跟蹤目標，但是相比較而言由于所提CFSWR算法考慮了特征不相關性和冗余性，所以跟蹤更為準確，這點從ironman序列第120幀中也得到了印證。

blurOwl序列的運動模糊效果主要是由于錄像過程中相機快速運動導致產生運動模糊效果，而david序列的運動模糊效果主要由人體相對于相機快速移動導致，可以發現在blurOwl序列的第154幀、370幀和david序列的第461幀、770幀時ASRCF、CCOT、GFSDCF、HDT、MCPF等算法大多發生一定程度的跟蹤漂移現象，而本文所提算法由于不僅采用了深度特征，而且在進行多層特征響應融合時還考慮到分辨率差異和特征不相關性剔除，所以在3個運動模糊挑戰序列中能夠精準跟蹤目標。

圖6 運動模糊

4.3.3 尺度變化場景算法性能分析

圖7所示為尺度變化情況下各算法的跟蹤效果，在doll序列中由于玩具離相機遠近不同導致所錄玩具的尺度差異比較大，這給目標尺度估計帶來了嚴峻的挑戰。在doll序列的第886幀中所提CFSWR算法的尺度估計最為準確，而HDT最差，這是因為CFSWR算法采用了一個尺度估計專用模型，在不犧牲速度的前提下實現高精度尺度估計，而HDT算法主要的是使用多層卷積特征融合，對于尺度估計方面僅采用單一的尺度因子進行控制，所以其尺度估計效果不佳。

dragonBaby序列的尺度變化挑戰主要是由于小孩在劇烈運動導致離鏡頭遠近不一所造成，而rubik序列中人在對魔方進行旋轉和相對鏡頭平移也導致所錄制的魔方的尺度不一致。在dragonBaby序列的第47幀和第85幀ASRCF算法均跟蹤失敗，這是由于ASRCF雖然考慮到多層特征融合但是由于其沒有考慮到特征不相關性，所以面對復雜的場景適應性較差。在rubik序列的第1362幀時由于魔方尺度和旋轉變化程度較大，所有目標尺度估計的準確度均受到較大影響，MCPF的尺度偏差最大，這是由于該算法雖然通過粒子采樣策略處理尺度變化，但沒有使用深度特征，在目標定位不準確情況無法進行良好的尺度估計，因此效果較差，而本文所提算法雖然尺度估計也出現了失誤，但由于其使用多層卷積特征融合且考慮到特征不相關性，所以其尺度估計失誤程度比較低。

圖7 尺度變化

4.4 算法時間復雜度

在算法設計中實用性評估是非常關鍵的環節，為了評估算法的實用性實驗中記錄了幾種算法的平均速度以進行算法時間復雜度評估，具體如表2所示。從表中可以看出ASRCF算法速度最快，這是因為其使用了雙路并行模型分別對算法的位置和尺度進行估計，其速度實時性得到了保障；CCOT算法于使用了三次樣條函數進行插值且每幀進行了五次串行尺度估計，所以其速度比較低，不能實時應用；MCPF算法雖然使用了傳統特征，但其采用了粒子采樣策略使得算法速度十分受限，也不能實時應用。而本文所提CFSWR算法既具備了CFSWR的雙路并行模型，又具備GFSDCF算法的特征選擇方法，其速度雖然由于進行特征不相關性和特征冗余處理時被降低，但最終測定平均速度也達到了10.1幀每秒，這個速度在實際工程中如果采用視頻抽幀法可以達到實時應用要求，因此本文所提算法可以應用于工程實踐。

表2 算法平均運行速度對比

5 結論

本文針對傳統核相關濾波算法采用多卷積特征響應融合、通道特征選擇、雙路模型分別進行定位和尺度估計等策略解決目標跟蹤過程中特征表征能力不足、特征冗余、尺度估計導致算法速度慢等問題，提高目標跟蹤的準確性和穩健性。本文具體創新點如下：①采用多層特征響應融合方式提高特征表征能力。②采用空間插值方法解決卷積層特征分辨率不同問題。③采用通道特征選擇策略解決通道特征不相關和冗余問題。④采用雙路模型進行目標定位與尺度估計使得算法在高精度尺度估計下速度幾乎不受影響。⑤在公開測試集上測試所提算法性能，經測試所提算法的準確性和穩健性良好。