部分聯網環境下交叉口混合動力汽車分層控制

錢立軍，宣 亮，陳 健，陳 晨

(合肥工業大學汽車與交通工程學院，安徽 合肥 230009)

1 引言

2019年全國汽車的保有量超過2.5億輛，由此導致化石能源大量消耗、環境污染、交通擁堵及汽車行駛安全等問題日益嚴重。電動化、智能化、網聯化、共享化是當前中國汽車工業發展的四大主題，并且推動我國混合動力汽車、智能交通系統、車聯網以及智能汽車等技術的快速發展[1]。信號路口是智能交通系統的重要組成部分，是城市交通網絡的關鍵節點，若對其進行協調優化控制，可以提高通行效率，減少車輛燃油消耗[2]。

國內外學者對車輛通過信號燈交叉口的通行安全及經濟性進行了大量的研究，其研究對象大致可以分為常規車輛、網聯車以及它們組成的混合車隊三類。當研究的對象全部由常規車輛即非網聯車組成時，研究人員基于車輛時延、隊列長度、飽和度等指標建立傳統的交通信號控制系統來改善車輛的經濟性[3]。當研究對象全部由網聯車組成時，車輛與交通系統可以實時通訊，車速可以根據得到的信息及時調整，從而具有良好的安全性和經濟性[4-6]。考慮到目前汽車產業發展現狀，網聯車全面普及還需要很長時間，現階段基于全部車輛聯網環境下設計的控制策略難以得到實際應用，但是對于設計部分車輛聯網環境下車輛的控制器有很大的參考價值。

在部分車輛聯網環境下，Omidvar等進行了獨立路口交通控制系統的部署和測試，對車輛在路口的安全性進行了驗證[7]；Yu等建立了混合車隊的一致最優速度咨詢模型，提高了車隊的安全性和經濟性[8]；Jiang等采用最優化算法對混合車隊進行車速優化，提高車隊的經濟性[9]；林培群等提出部分聯網環境下交通流向動態組合的路口自適應控制方法，提高了混合車隊的通行效率[10]。現有的控制策略主要針對低流量工況或者研究對象是少量的車輛[11]，對中、高及過飽和車流量工況的適應能力有限。

本文面向部分車輛聯網環境下中、高及過飽和車流量工況，設計了分層控制器。在目標車速控制器中，基于模型預測控制(Model Predictive Control，MPC)策略和吉布斯(GIPPS)跟車理論，得到車輛的最優車速；在能耗控制器中，結合混合動力車輛的加速和制動信息與變等效因子的等效燃油消耗最小策略對電機和發動機進行最優功率分配。搭建MATLAB/VISSIM聯合仿真模型和混合動力汽車硬件在環平臺，在中、高及過飽和車流量工況下進行硬件在環試驗。

2 車輛分層控制器設計

本文研究的信號燈交叉口的如圖1所示，包含了檢測器、控制器、信號燈、網聯與非網聯車輛等。

圖1 信號燈交叉口示意圖

分層控制器由初始輸入、目標車速控制器和能耗控制器組成，如下圖2所示。

目標車速控制器的核心思想是通過優化混合車隊中網聯車的速度分布來優化整個交通流，它可以通過檢測器傳遞的信息識別混合車隊中車輛的類型，與其中的網聯車以及智能交通設施進行信息通信，接收車輛信息如初始位置、初始速度以及信號燈正時，并向網聯車發送速度信息。非網聯車是當前現實世界中的常規車輛，假設其為自動駕駛車輛并且網聯車與非網聯車在道路上的分布是隨機的，二者都為混合動力汽車，其參數如表1所示。

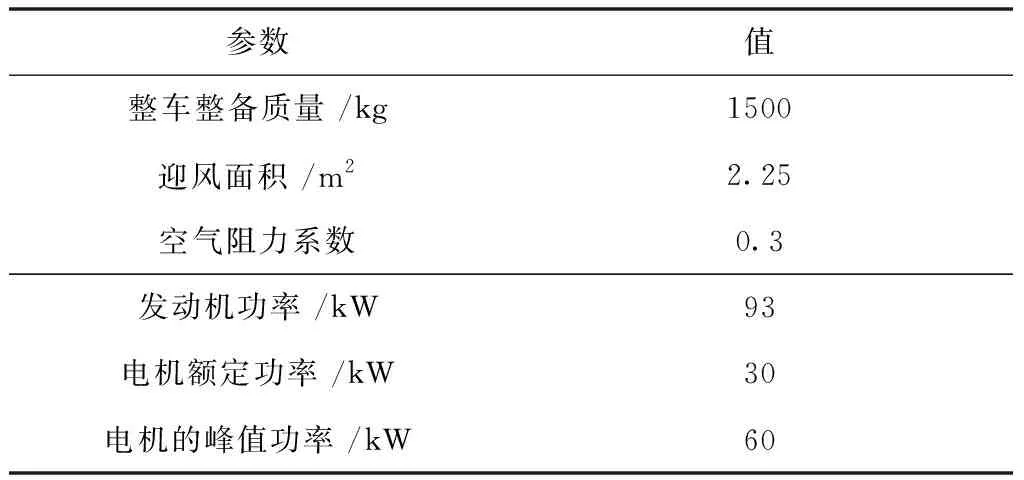
表1 車輛參數

圖2 部分車輛聯網系統分層控制器

能耗控制器利用接收到的最優目標車速計算出車輛的加速和制動信息，基于變等效因子的等效燃油消耗最小策略對當前電機功率和發動機功率進行最優分配，隨后將控制指令發送給電機控制器和發動機控制器，從而實現電機與發動機的最佳控制，進而提升混合動力汽車的經濟性。

3 目標車速控制器

在目標車速控制器中，網聯車的控制是基于車聯網利用目標車速控制器獲取車輛當前位置、速度以及綠燈剩余時間，采用信號燈正時(Signal Phase and Timing，SPaT)方法求解目標車速并將其作為求解最優目標車速的初值，隨后基于模型預測算法求解得到最優目標車速，依據當前車速與目標車速的差值進行加/減速度的計算，獲得下一時刻車輛速度與位置。非網聯車不能通過目標車速控制器獲得外界信息，但是可以通過自身的傳感器獲得前后車距、前車速度以及信號燈信息，利用得到的信號燈信息、當前車速、當前車輛位置與前車位置、前車速度相結合，基于GIPPS跟車理論，計算車輛的加速度或者減速度，從而得到下一時刻車輛速度和位置。

3.1 網聯車最優目標車速求解

網聯車的控制目標函數是基于MPC建立的包含車速、位置、油耗等多目標優化函數，在避免車輛遇到信號燈停車以及提高燃油經濟性的前提下，求得最優目標車速以及車輛位置。車輛動力學方程、車輛功率平衡方程、車輛能耗模型以及目標車速模型是求解最優目標車速函數的基礎，在建立模型過程中會使用。

3.1.1 建模基礎

混合動力車輛的動力學模型如下所示[12]

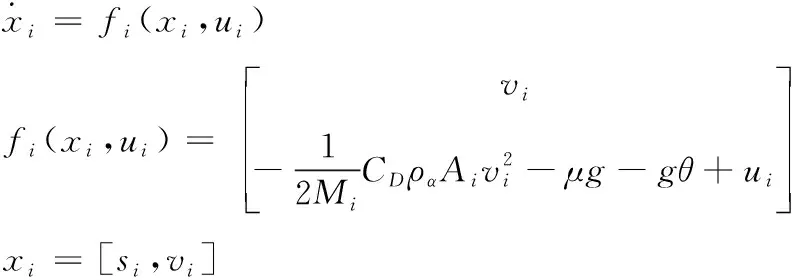
(1)

式中，xi為車隊第i輛車的狀態向量；ui為車隊第i輛車的控制變量，是車輛的單位質量牽引力或制動力；vi為車隊第i輛車的速度；Mi為車隊第i輛車的質量；CD為車隊第i輛車的迎風阻力系數；ρα為空氣密度；Ai為車隊第i輛車的迎風面積；μ為車輛的滾動阻力系數；g為重力加速度；θ為道路坡度。

車輛的功率平衡方程如下所示

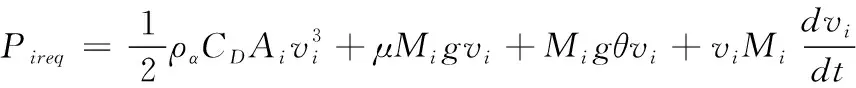
(2)

式中Pireq為驅動需求功率。

以車輛單位距離的能量消耗最小值為目標，建立數學模型如下式(3)所示[13]

(3)

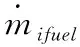
在求解最優目標車速時，需要基于SPaT獲得的目標車速作為計算的初值，其表達式如下[14]

vimin≤viobj(td)≤vimax

tc=tg+tr

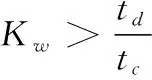
(4)

式中，viobj為車隊第i輛車的目標車速；dia(td)為車隊第i輛車與交通信號燈的距離；Kw為交通信號燈的循環次數，取整數；tc為一個紅綠燈周期的時間；td為車輛行駛的時間；tg、tr分別為綠燈和紅燈的持續時間。

分析式(4)可知，當信號燈發生變化時，目標車速也會發生相應的變化。當信號燈為綠燈時，若車速在不超過最大允許值的前提下可在綠燈持續時間內行駛過車輛與信號燈的距離，此時目標車速為車速最大值。當車輛不能在綠燈持續時間內通過信號燈路口，此時減速，經過一個紅燈持續時間段的行駛，隨后在下一個綠燈持續時間段內通過信號燈路口。若車輛減速后經過一個紅燈持續時間段的行駛依然會提前到達信號路口，則會在路口停車，并在下一個綠燈時通過路口，這里發生停車的原因是因為設置了車速下限，此時目標車速需要按式(4)重新計算。

3.1.2 基于MPC的最優目標車速求解

網聯車最優目標車速的求解是一個典型的多目標優化求解問題，求解時需要考慮汽車的油耗、車速跟隨、控制變量、車與車之間的相對距離等相關因素的影響，本文用四者的加權之和構建目標函數。以單個車輛為對象，在時間段T內，汽車經過時間td的行駛后，車速最優化的目標函數可以用式(5)表達，該式的輸出包括當前時刻車輛的目標車速及位置，車輛的狀態變量為當前車輛的加減速度[15]。

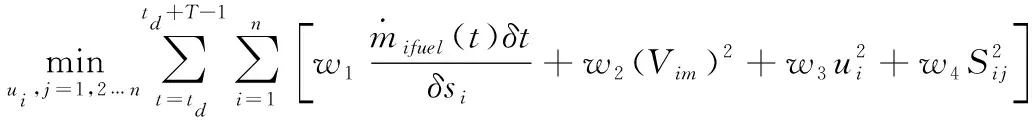
(5)

δsi=si(td+T-1)-si(td)

Vim=vi(t)-viobj(td)

Sij=S0+thvi(t)-(sj(t)-si(t))

vimin≤vi(t)≤vimax

uimin≤ui(t)≤uimax

(6)

式(5)、(6)中，δsi為車隊第i輛車在T時間段內的行駛距離；Vim為車隊第i輛車當前車速與目標車速的差值；Sij為車隊第i輛車和第j輛車的相對距離；si(t)和sj(t)分別為第i輛車和第j輛車在時間t時的位置；th為預設的前后兩車的間隔時間；S0為預設的兩車安全距離；wi(i=1，2，3，4)為加權系數。

車速最優化的目標函數式(5)中加權系數w1、w2、w3、w4分為對應的車輛油耗、車速、控制變量、前后車相對距離。當研究對象的目標車速范圍較大，研究傾向于使車輛的燃油經濟性最優而不是車速跟隨效果更好時，此時w1取較大值而w2取較小值；當研究對象的目標車速范圍變化較小，研究傾向于使車輛的車速跟隨效果更好而不是燃油經濟性最優時，此時w2取較大值而w1取較小值。當前后車相對距離增加時，w4取值較小，反之，w4取值較大。w3取常數值。目標車速的取值范圍對車速最優化的求解有兩個方面的影響，一是影響加權系數w1和w2的取值，二是當車輛的實際車速與最優目標車速差距太大時，通過取值范圍限制將車速變化限制在規定的區間里，避免在交叉口遇到紅燈停車。

上述優化問題不僅要滿足式(6)的約束，還要滿足式(1)動力學方程的約束。值得注意的是，上一小節基于SPaT求解目標車速的目的是避免在路口停車，沒有考慮車輛的燃油經濟性，而本小節求解的最優目標車速綜合考慮了車輛燃油經濟性、車速跟隨以及前后車跟車距離。

3.2 非網聯車的目標車速求解

如圖2所示，當檢測到道路上行駛的車輛是非網聯車時，采用GIPPS跟車理論進行速度控制。輸入包括瞬時速度與位置、交通信號的定時信息以及前車的速度和位置信息。GIPPS跟車理論公式如下式(7)所示[16]。

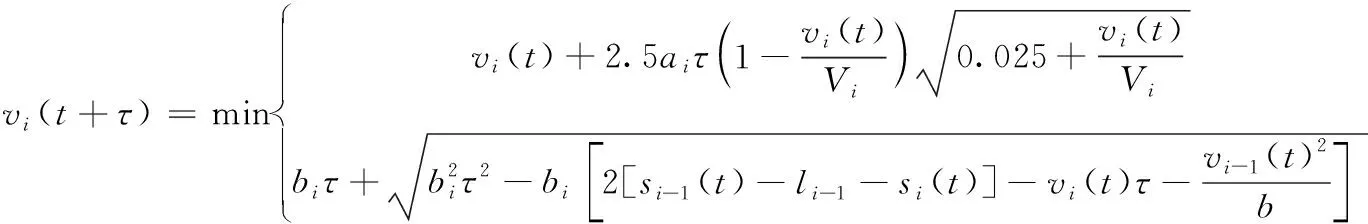
(7)

式中ai為車隊第i輛車的最大加速度；bi為車隊第i輛車的最小加速度；Vi為車隊第i輛車的期望車速；τ為時間間隔；si(t)為車隊第i輛車在t時刻的位置；li-1為車隊第i-1輛車的車身長度；b為理想的制動減速度。

4 能耗控制器

能耗控制器利用接收到的目標車速計算加速和減速信息，進而對電機與發動機進行最優功率分配。混合動力汽車的能耗控制器的控制策略有很多，例如基于規則的、基于優化算法的、基于工況等多種，本文選用基于變等效因子的等效燃油消耗最小策略。

等效燃油消耗最小策略是基于啟發式經驗提出并被應用于混合動力汽車的控制系統，其核心將發動機燃油消耗和電能消耗歸結為統一的能耗指標，從而解決能量的實時最優分配，理論可以用式(8)描述[17]：

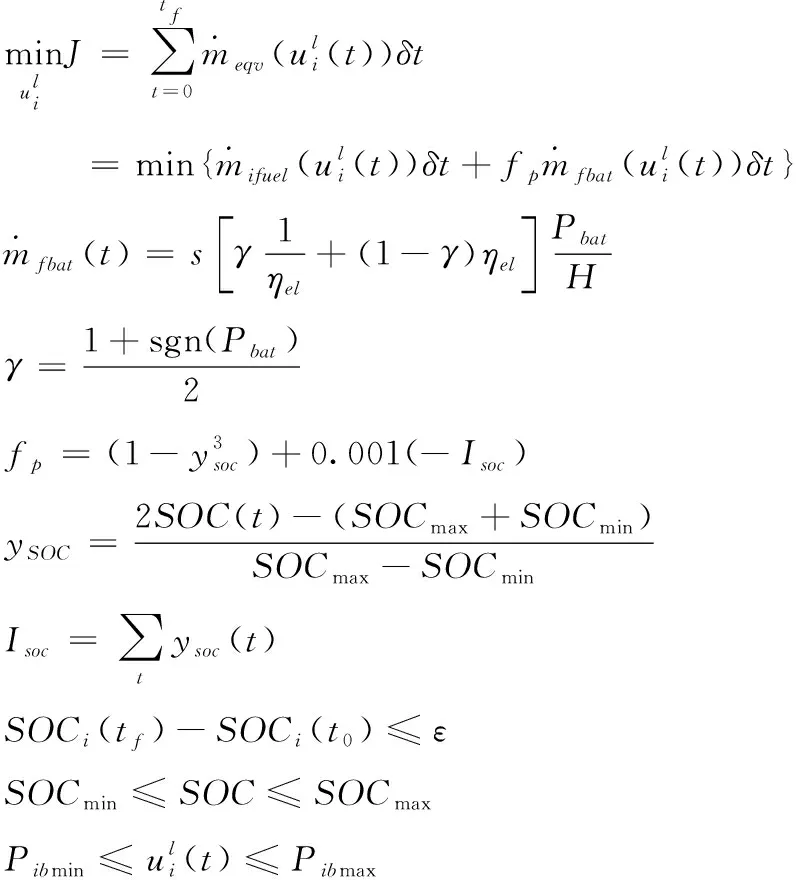
(8)

等效燃油消耗最小策略中的等效因子s是定值，通過計算協態變量獲得，但是定等效因子對工況的適應性很差，所以需要設計一個變等效因子以滿足不同工況的需求。本文采用線性迭代的方法計算變等效因子，其表達式如下式。

s(t+1)=0.5(s(t)+s(t-1))+cp(SOC(t0)-SOC(tf))

(9)

上式中，cp為迭代步長。

5 硬件在環仿真結果與分析

5.1 硬件在環仿真設置

本文仿真采用塔式工作站(戴爾T7920，處理器36核，2顆至強金牌5220，運行內存64G)來計算目標車速控制器中網聯與非網聯車的車速，將仿真得到的車速保存為數據格式并將其用于能耗控制器的離線仿真。離線仿真為dSPACE硬件在環仿真，仿真時間設置為400s，仿真系統如圖3所示。

圖3 硬件在環仿真系統

利用VISSIM和MATLAB建立聯合仿真平臺。在軟件仿真程序中，對微觀仿真環境進行如下設計：測試網絡是一個假設的路口，如圖1所示；在仿真中不允許換道和轉彎行為。VISSIM模擬交通并為MATLAB控制算法生成輸入，仿真過程中使用的參數如表2所示。

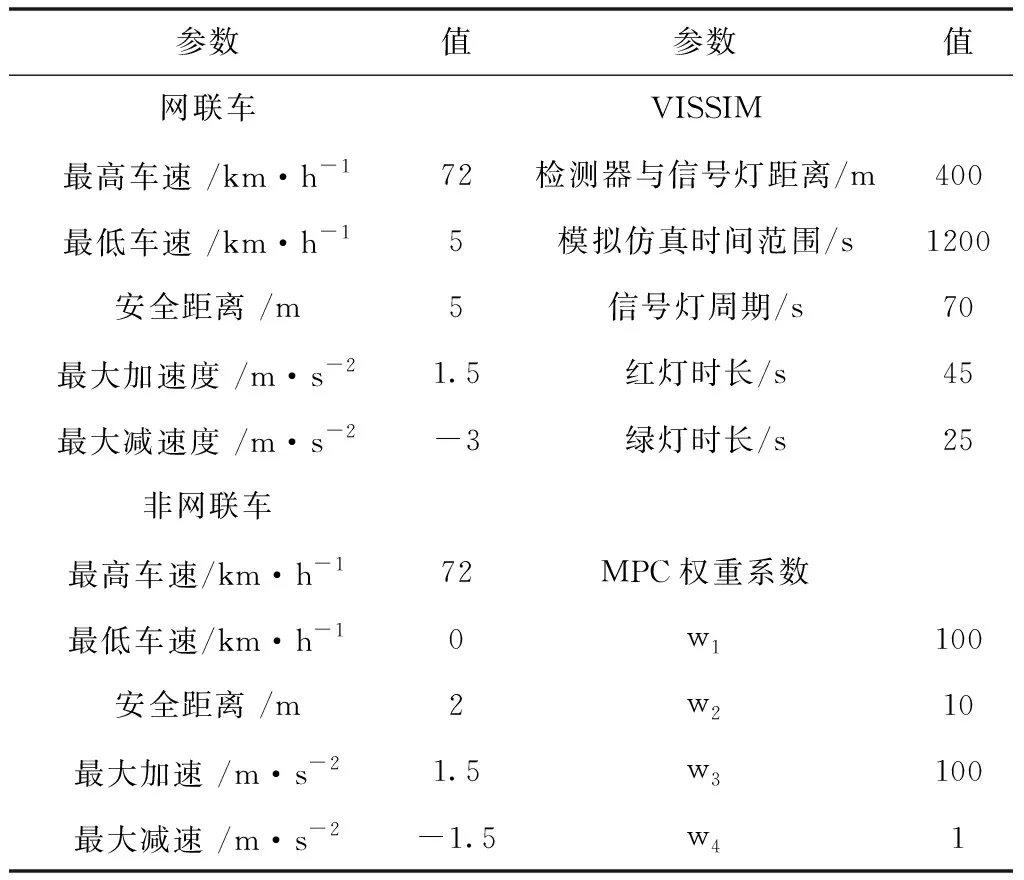
表2 仿真參數

5.2 硬件在環仿真結果

本文在中、高及過飽和車流量工況下進行了仿真分析。當車流量低于400 veh/h時，為低車流量工況，當車流量為400 veh/h～1000 veh/h時，為中高車流量工況，當車流量高于1000 veh/h時，為過飽和車流量工況。

當道路上的車流量為600 veh/h時，網聯率從0以10%為間隔遞增到100%時，車輛在信號路口的典型通行軌跡情況如圖4-圖9所示，車輛的燃油經濟性如表3所示。

圖4和圖9分別是0網聯車與100%網聯車的通行軌跡，都沒有發生軌跡相交的情況，并且圖9中網聯車通過路口時沒有停車，說明設計的車輛分層控制系統可以很好的適應全網聯環境，同時也可以保證全非網聯車環境下的通行安全性。圖5和圖6分別是網聯率30%和50%時車輛的通行軌跡，可以看出其中都發生了停車的情況。圖7和圖8分別是是網聯率60%和70%時車輛的通行軌跡，車輛在通過路口時都沒有發生停車。綜合圖4至圖9，可以看出，不論網聯率如何變化，車輛都可以安全的通過路口，說明當前設計的車輛控制系統是合理的，可以滿足不同網聯率情況下車隊在道路上的安全行駛，同時網聯率大于等于60%時，可以實現車輛在信號燈交叉口不停車通行。

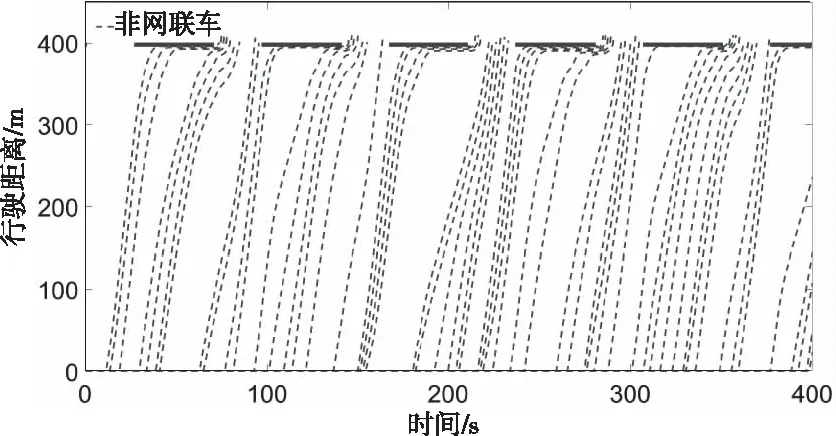
圖4 0網聯率的通行軌跡

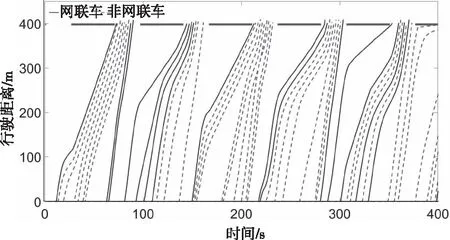
圖5 30%網聯率的通行軌跡

圖6 50%網聯率的通行軌跡

圖7 60%網聯率的通行軌跡

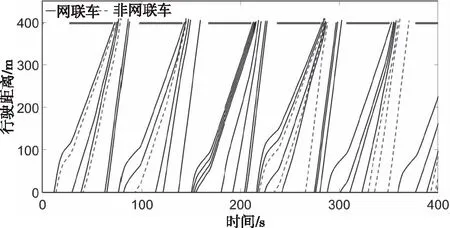
圖8 70%網聯率的通行軌跡

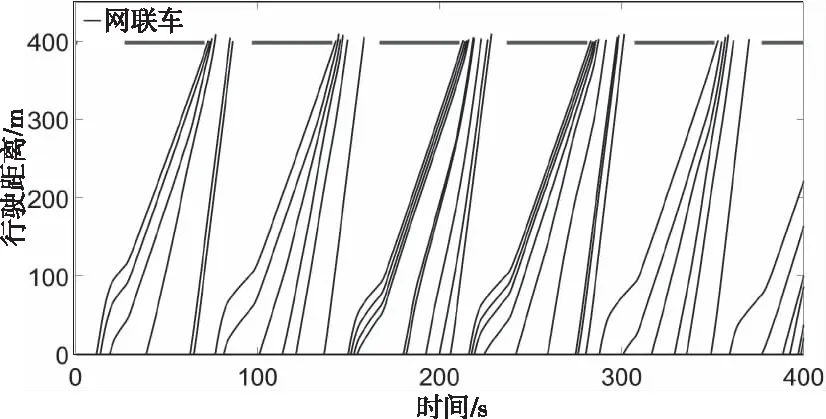
圖9 100%網聯率的通行軌跡

表3是當車流量為600 veh/h時不同網聯率時車輛的燃油經濟性。分析可知，網聯率在0到60%之間時，網聯率每提升10%，經濟性平均提高5.2%，而網聯率從60%提高到100%時，經濟性平均提高0.49%。隨著網聯率的增加，車輛的百公里油耗呈現下降的趨勢，但網聯率高于60%時，車輛的百公里油耗趨于穩定。經濟性提升的結果表明，當道路上只要存在網聯車，采用該分層控制器就可以改善車輛的燃油經濟性，當網聯率高于60%以后，再繼續增加車輛的網聯率，車輛的燃油經濟性的提升效果不夠顯著。

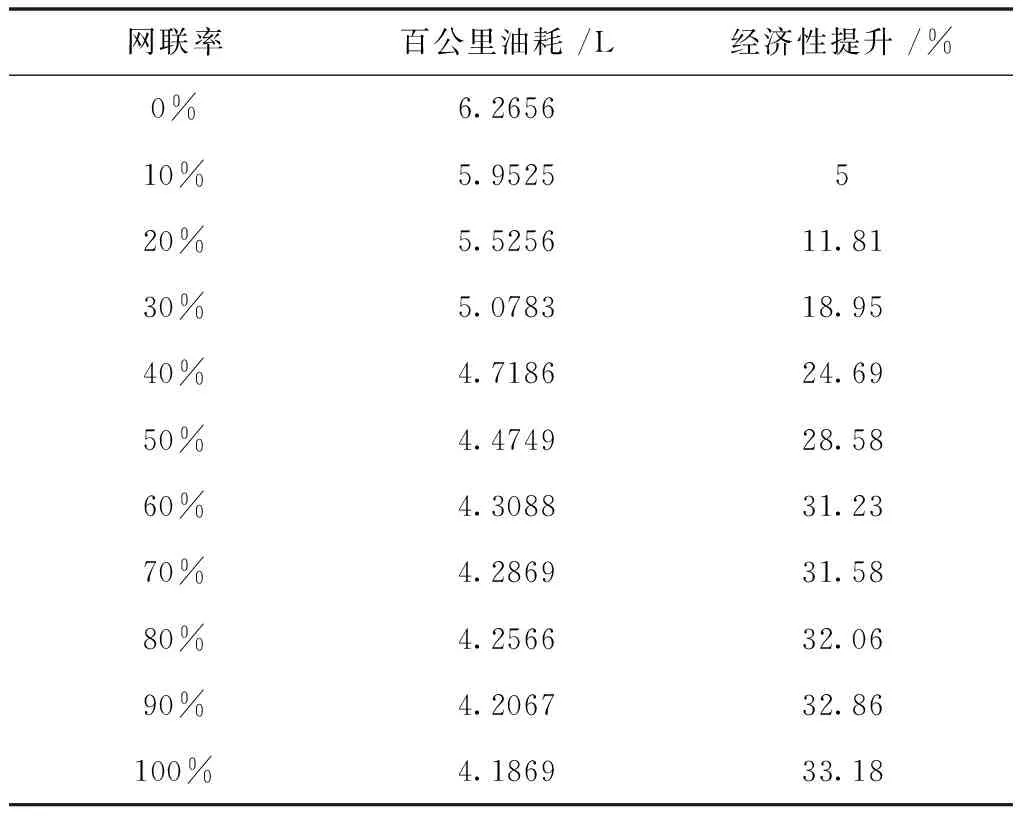
表3 不同網聯率下的燃油經濟性

圖10 不同車流量條件下燃油經濟性

為了檢驗本文設計的分層控制器對其車流量的是否有相同的效果，對900 veh/h與1200 veh/h的車流量進行了實驗，其燃油經濟性及提升結果與600 veh/h的車流量對比如圖10與圖11所示。在車流量900 veh/h時，網聯率為60%和100%時，經濟性分別提升了33.12%和35.27%，網聯率在0到60%之間時，網聯率每提升10%，經濟性平均提高5.52%，而網聯率從60%提高到100%時，經濟性平均提高0.54%；在車流量1200 veh/h時，網聯率為60%和100%時，經濟性分別提升了37.7%和40.12%，網聯率在0到60%之間時，網聯率每提升10%，經濟性平均提高6.35%，而網聯率從60%提高到100%時，經濟性平均提高0.5%。綜合不同流量下的燃油經濟性分析結果可知，網聯率60%是車輛的經濟性提升的拐點。網聯率相同的條件下，道路上車流量由600 veh/h增加到1200 veh/h時，車輛的百公里油耗增加，經濟性提升的幅度也更大，這說明本文的分層控制器對大車流量的經濟性的改善效果好于小車流量。

與文獻[9]中的最優化控制方法對比如下圖12所示，在網聯率低于30%時，文獻[9]經濟性提升比本文方法略好，而網聯率高于30%時，采用本文方法經濟性提升效果好于文獻[9]方法。

圖12 經濟性提升對比

6 結論

本文提出了一個部分車輛聯網環境下的信號燈路口的分層控制器。在不同車流量的工況下，車輛采用該分層控制器能安全通過信號燈路口。當網聯率高于60%時，車輛能夠在綠燈窗口時間完成通過路口。

隨著網聯率的提升，車輛的燃油經濟性顯著改善，網聯率60%是經濟性提升的拐點。在此基礎上，網聯率的提升對經濟性改善效果趨于穩定，并且本文設計的分層控制器對大流量工況的經濟性改善效果更優。