一種基于偽距殘差加權的最小二乘定位算法

秦明峰，胡麗格

(1. 衛星導航系統與裝備國家重點實驗室，河北石家莊 050081；2. 中國電子科技集團公司第五十四研究所，河北石家莊 050081)

1 引言

導航與位置服務在物聯網、智慧城市、公共安全和救災減災等領域發揮著基礎性支撐作用，雖然全球衛星導航定位系統(GNSS)可以在室外提供較高的導航定位精度，但面對復雜的室內場景，GNSS信號由于遮擋和多徑，其定位效果不如室外[1，2]。但是現代社會人們四分之三以上的時間都是室內活動，室內高精度、高穩定性和高連續性的導航與位置服務有著廣闊的發展前景。為此，開展室內復雜環境下的定位導航服務技術研究有著重要的意義[3]。

室內定位需要考慮在室內的復雜環境下高精度、低成本和實現復雜度低等方面的要求，常見的室內定位技術有：紅外線[4]、超聲波[5]、藍牙[6]、WIFE[7]、ZigBee[8]、偽衛星[9]、地磁[10]、慣導[11]、視覺[12]和UWB[13]等室內定位技術。UWB定位技術[14]根據測得定位標簽相對于兩個不同定位基站之間無線電信號傳播的時間，從而得出定位標簽相對于定位基站的距離，通過多個距離進行定位，由于UWB的信號體制能夠有效抑制多徑，因此可實現6-10cm的定位精度[15]，在室內定位領域有較好的應用前景。但是受室內建筑布局、結構材料、裝修等影響因素，UWB基站收到的測距信號未必是直達信號，這樣的信號參與定位必然會影響室內定位的定位精度。應用在UWB室內定位中的定位方法主要有最小二乘算法[16]、迭代最小二乘算法[17]和卡爾曼濾波算法[18]，最小二乘和迭代最小二乘算法不能消除非直達信號對定位精度的影響，卡爾曼濾波算法需要首先建立復雜環境模型，當環境發生變化時需要對模型進行修改，實現較為復雜。

本文從UWB定位的定位原理出發，結合室內導航定位的特點，提出一種基于偽距殘差的最小二乘加權算法，該算法基于偽距殘差通過自適應調整最小二乘加權的權值，來降低非直達信號對最小二乘定位的影響，實驗結果表明：該算法能夠有效提升室內復雜環境下UWB定位的定位精度和定位穩定性。

2 室內UWB導航定位模型

UWB測距技術可分為兩類：單程測距和雙程測距，單程測距應用于基站之間需要時鐘同步，基站構建實現起來較為復雜，但是能夠支持更多的標簽卡同時定位，該方式誤差更多來源于基站網絡的時鐘同步精度。雙程測距不需要基站進行時鐘同步，采用計算收發時間的方式測定基站與標簽卡之間的距離，該方式實現較為簡單，目前情況下實現的精度相比單程測距要高，但是能夠同時支持的定位標簽卡有數量限制。下面簡要介紹一下UWB定位的定位原理。

通過測量從載體到三個或更多個UWB基站傳播時間的方法，可以獲得載體到基站的距離，分別以每個基站為中心、以到每個基站的距離為半徑繪制三個或多個圓，多個圓的交點即為載體的位置。如圖1所示。

圖1 基于TOA的UWB定位原理

載體與基站的距離關系可表述為

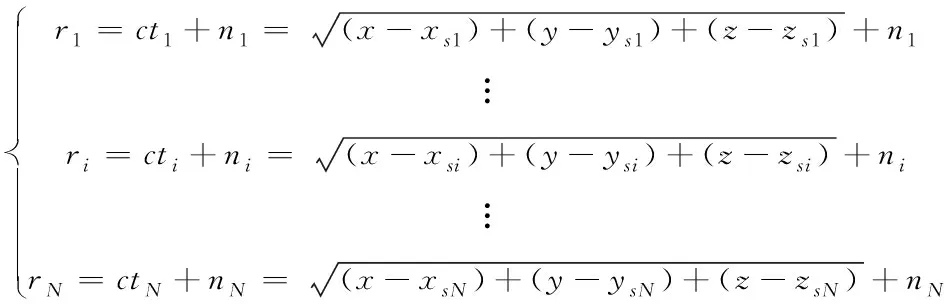
(1)

其中，(x，y，z)為載體位置坐標，(xsi，ysi，zsi)為第i個基站的位置坐標，c為電磁波傳播速度，ti為載體信號到達第i個基站的時間，ni為系統噪聲，N為基站數量，ri為載體到第ri個基站的距離。

將式(1)轉換成關于載體坐標的線性模型，對式(1)兩邊分別求平方，進行變換可以得到

(2)

令

(3)

T=(x2+y2+z2)

(4)

將式(3)和(4)代入到式(2)，進一步展開可得

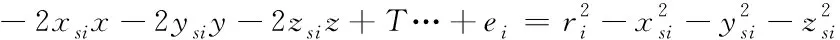
(5)

將N個基站的位置距離關系寫成矩陣可得

H=AX+e

(6)

其中，X=[x，y，z，T]T，e=[e1，e2，…，eN]。

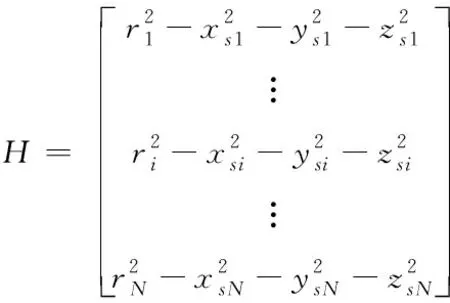
(7)

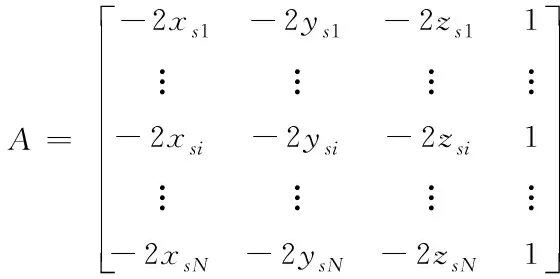
(8)

3 最小二乘的定位算法

最小二乘算法[19，20]最早由最早是在1975年由高斯(Karl Gauss)在測量恒星軌道時提出，該算法通過最小化平方和求解最優解，并使得這些求得的數據與實際數據之間誤差的平方和為最小，由于具有較好的普適性和穩定性，且實現較為簡單，在信號處理中有著廣泛的應用。

最小二乘算法是構造使誤差平方和最小的函數，因此，構造代價函數為

J=E(eTe)=(AX-H)T(AX-H)

(9)

進一步展開可變為

J=XTATAX-2XTATH+HTH

(10)

使上述代價函數最小的解即為當前載體的位置坐標，即

(11)

對上式進行求導，對應極值即為載體位置坐標，即

(12)

最后可得到方程的最優解為

X=(ATA)-1AH

(13)

該解即為最小二乘算法得到的最優解。

4 基于偽距殘差加權的最小二乘算法

當UWB信號在室內傳輸時，由于室內環境的復雜性，容易受到反射、衍射和多徑等多種因素的影響，上節中介紹的最小二乘算法定位精度將嚴重降低，這是因為最小二乘算法針對的是服從正態分布觀測樣本，當觀測值有悖于正態分布假設、樣本遭受異常污染時，最小二乘估計不具有抗干擾性。為了改善最小二乘在費直射情況下的定位精度，需要對算法進行改進，提升算法在個別基站信號非視距條件下的算法的穩定性。

可通過對最小二乘算法的各個基站的數據進行加權降低非直達信號對定位結果的影響。即將式(13)改寫為

X=(ATWA)-1AWTH

(14)

加權是為了降低非視距信號對最小二乘定位結果的影響，但是，環境是不斷變化的，傳統的固定加權或根據測距距離的加權無法消除非視距信號對定位的影響。當某個基站的偽距測量值不是直達信號時，測量偽距變化和估算偽距變化之間的差值變大，因此，可用偽距變換率的殘差構造隨殘差變化的權值矢量，自適應降低非直達信號對最小二乘定位的影響。

偽距殘差的構造方法可描述為：假設k時刻載體的位置坐標為(xk，yk，zk)，N個基站的測量偽距分別為r1，k，…ri，k，…，rN，k，k+1時刻載體的位置坐標為(xk+1，yk+1，zk+1)，N個基站的測量偽距分別為r1，k+1，…ri，k+1，…，rN，k+1。設

(15)

(16)

其中，Δxk=xk+1-xk，Δyk=yk+1-yk，Δzk=zk+1-zk。

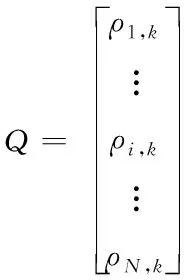
(17)

其中，ρi，k=ri，k+1-ri，k為k到k+1時刻偽距的變化率。

建立偽距變化量的觀測方程

Q=Fv+ε

(18)

其中，ε為偽距變化和位置估算不一致引起的誤差。

定義估計的偽距殘差為

ε=Q-Fv

(19)

當所有基站的偽距測量為直達徑時，ε應為接近于0很小的值，當收到的某個基站的信號為非直達徑時，ε對應該基站的偽距殘差值變大，因此，可根據偽距殘差的變化構造加權向量，約束最小二乘算法性能。

則偽距殘差的方差為

R=E[εεT]=(Q-Fv)(Q-Fv)T

(20)

令

(21)

構造最小二乘加權的約束函數。

基于殘差加權的最小二乘法算法流程如圖2所示。

圖2 基于殘差的最小二乘算法流程

可描述為：

1) 獲取能收到節點的測距結果；

2) 判斷節點數量是否≥3，若≥3，進行定位，否則該次數據無法實現定位；

3) 構建觀測量F和Q，并計算偽距殘差協方差矩陣，并根據參加協方差矩陣構建加權矩陣W；

4) 構建觀測矩陣A和H，根據式(14)計算定位結果，并輸出定位結果。

5 室內定位性能試驗

5.1 實驗環境介紹

在有走廊、門廳和實驗室的樓內布設UWB接收基站，具體位置如圖4紅色點位所示。由全站儀標定基站的精確位置，標定精度在毫米量級。區域內的每個位置點至少有三個以上的基站能夠實現視距接收。行走的真實軌跡事先由全站儀進行標定，圖中黑線基站無遮擋條件下定位精度的驗證軌跡，紅線為部分基站有遮擋條件下的驗證軌跡。

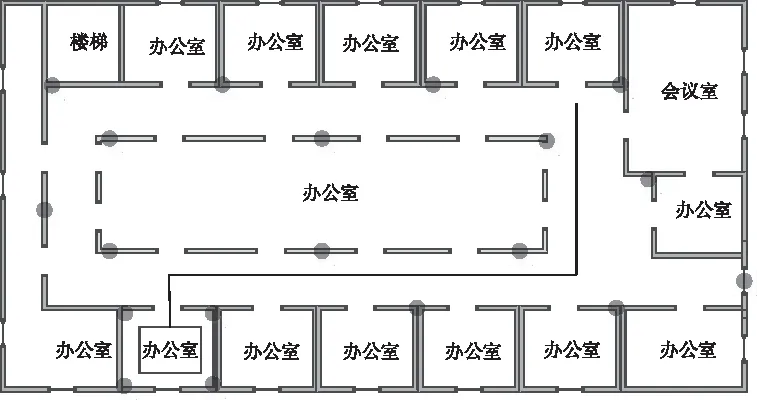
圖3 實驗環境及設備安裝位置示意圖

圖3給出實驗環境及設備安裝位置布局示意圖，圖中紅色圓點表示安裝的UWB基站。實驗采用基于雙向測距的UWB定位設備，該測距方式不需要考慮基站和標簽之間的時間同步問題，實現較為簡單，有助于降低硬件成本。為了消除系統誤差，在用全站儀標定好基站位置后，再標定一些點位，消除基站測距誤差的影響。每個點位采集100次測距結果，采用中值濾波計算距離觀測值的絕對誤差，通過不同點的最小二乘擬合得到每個基站的測距補償值。

5.2 室內無遮擋簡單環境的導航定位實驗

首先在一個室內尺度較小的方形無遮擋區域架設4顆UWB接收基站，在定位中僅采用這四個基站的測距結果，在3m×4m的房間內沿圖3中黑線運動，在無遮擋條件下UWB定位如圖4所示。

圖4 室內無遮擋方形區域定位圖

從上圖可以看出：在無遮擋所有基站都是收到直達信號的條件下，最小二乘(LS)，非線性最小二乘(NLS)[21]和基于殘差加權最小二乘算法(RWLS)都具有較好的定位性能，定位性能并無明顯差別，定位精度均優于10cm。

為了對比分析以上三種算法的定位性能，利用位置誤差的絕對值，誤差的均方根等進行分析。首先分析在參與定位所有基站無遮擋環境下導航定位精度，如表1所示。

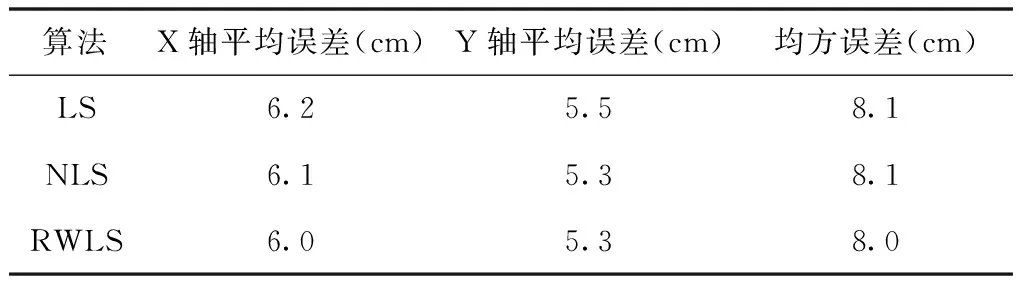
表1 定位誤差的實驗結果

從上表中可以看出：在無遮擋條件下，三種算法定位精度相差不大，均優于10cm。

5.3 室內有遮擋復雜環境下的導航定位實驗

實驗2標簽的運行軌跡如圖3中紅線所示，由于實際運行軌跡是由事先標校的離散定位點連線形成的線段，為了分析本文提出算法的定位精度，將線段分為幾段直線并進行線性插值，并讓總點數等于該運行軌跡內定位解算的點數，通過定位結果與最近的插值點比較確定算法的定位精度。如下圖所示：

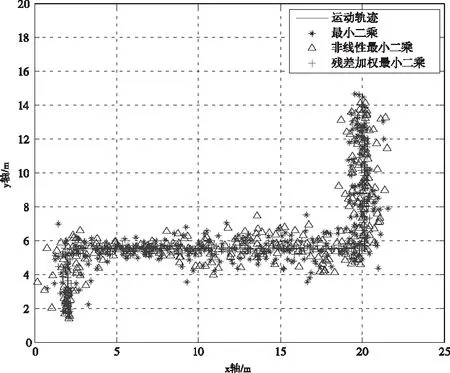
圖5 室內收到多個非直達信號的定位圖

從圖5中可以看出：最小二乘、非線性最小二乘算法在存在多個非直達信號的條件下，定位結果存在一定的發散情況，定位精度變差而本文提出的基于偽距殘差加權的最小二乘算法能夠有效降低非直達信號對定位精度的影響，在室內復雜環境下具有更好的收斂性。

進一步分析在有部分基站收不到直達信號的條件下的定位精度，如表2所示。

表2 定位誤差的實驗結果

從上表中可以看出：在有遮擋條件下，最小二乘算法的均方誤差在59cm左右，非線性最小二乘算法的定位精度略優于最小二乘，但是兩者定位精度基本在一個量級，本文提出的基于偽距殘差加權的最小二乘算法的定位精度為17.8cm，明顯優于前兩種算法的定位精度。

6 結束語

針對室內復雜環境下的導航定位，在分析最小乘算法的基礎上，結合UWB定位的特點，提出一種基于偽距殘差加權的最小二乘室內導航定位算法，在有足夠參與定位測距值的條件下，該算法能夠有效消除非直達信號對UWB定位精度的影響，提升了算法的魯棒性。實驗結果表明：該算法在室內復雜環境下具有較好的定位精度，不存在非直達信號的條件下定位精度優于10cm，存在多個非直達信號的情況下，定位精度優于20cm，能夠滿足室內高精度導航定位的需求。