基于矩陣張量積的輕量網絡數據傳輸加密方法

俞興木，鄭旭飛

(1. 重慶人文科技學院計算機工程學院，重慶 401524；2. 西南大學計算機與信息科學學院，重慶 400715)

1 引言

網絡數據傳輸技術廣泛應用在工業、醫院和國防等重要領域[1]，傳感器是組成無線傳感器網絡的最小單位，網絡規模越大、網絡環境越復雜，網絡通信過程中所具有的挑戰性就越大。隨著網絡在各個領域的推廣，傳感器節點所產生的弊端越來越突出，并且在網絡傳輸過程中數據的安全性及隱私性也備受關注[2-4]。

為了提高無線傳感器網絡通信過程中的效率、安全性及保密性，大量研究者從壓縮感知加密方法出發，以此為基礎，構建基于壓縮感知的數據傳輸加密算法。文獻[5]針對數據傳輸過程中受到的篡改攻擊，基于里德-所羅門碼對篡改進行定位，并對數據進行恢復，結合壓縮感知輕量級加密方法對終端數據加密，保證數據的保密性，并對測量值進行局部歸一化處理，實現能量值的高強度加密，利用壓縮感知和RS特性實現數據的雙重篡改恢復，實驗結果表明該方法具有廣泛的適應性。文獻[6]設計了由預加密和嵌入兩階段構成的加密方法，通過Arnold置亂和Sine映射所產生的受控矩陣對數據進行加密與壓縮，為減少數據所承受的攻擊，利用伯恩斯坦多項式對嵌入階段的密文圖像進行處理，將其隱藏到載體圖像中，提高加密算法抵抗攻擊的能力，實驗結果表明，該方法具有較高的安全性。文獻[7]采用離散小波變換對數據進行稀疏化處理，基于壓縮感知方法加密和測量稀疏矩陣，并加入隨機數，對矩陣進行Hilbert置亂操作，將加密后的圖像隱藏到載體圖像中，實驗結果表明，該方法具有較好的魯棒性，應用范圍較廣泛。

基于以上研究，壓縮感知為網絡數據傳輸的加密技術提供了關鍵性的支持，可以解決無線網絡的安全性和適應性等問題，因此提出基于矩陣張量積的輕量網絡數據傳輸加密方法。基于矩陣張量感知理論，引入輔助矩陣，實現靈活觀測信息，結合TCP加密算法，提高數據傳輸的加密效率與安全性。

2 壓縮感知技術

為保證數據采樣精度，通常使采樣信號的頻率高于最高信號頻率的兩倍，但這種方式采集的信號具有較高的冗余度。為了提高空間的利用率，需要對這些數據進行壓縮，然后再進行使用。然而壓縮感知不僅可以對稀疏信號降維，還可以通過重構算法將數據恢復成原來的信號。壓縮感知過程如圖1所示。

圖1 壓縮感知過程

Rn×nmx

x=Ωa

(1)

其中，a∈Rn×n表示信號x在標準正交變換域Ω中的b個稀疏信號(b表示非零項的個數)，良好的正交變換域可以保證信號稀疏化的效果。

壓縮觀測的過程中通過測量矩陣Ψ對信號x線性投影，公式可表示為

y=Ψx=ΨΩa=Ζa

(2)

其中，Ψ表示與稀疏矩陣Ω不相關的測量矩陣；Ζ表示感知矩陣。測量矩陣對壓縮感知過程中信號精度的恢復有著重要的作用，為了使信號具有唯一性，測量矩陣應滿足Spark性質、非相干性質和有限等距原則這三個約束條件。

Spark性質是滿足信號重構成功的首要條件，用公式表示為

(3)

相干性質可通過兩個列向量的歸一化內積最大絕對值表示，公式可表示為

(4)

其中，βi，βj表示任意的兩個列向量，α(Ζ)的值越大，表示矩陣列向量相關性越高；反之，相關性越低，因此通過相干性可以構造出較好的指導測量矩陣。

有限等距原則表示若所有b階稀疏矩陣均小于一個最小常數，那么矩陣Ζ滿足b階有限等距原則，公式可表示為

(5)

其中，χb表示約束等距常數。只要滿足上述三個約束條件，就可以保證原始信號的重構。信號的重構恢復是將壓縮后的低維采樣信號恢復為原始信號的過程，公式表示為

(6)

為了轉化成凸優化問題，進一步將公式表示為

(7)

在數據傳輸過程中，數據信息具有冗余度高和可壓縮性等特點，通過數據信息的低采樣，降低成本。對于數據的稀疏化操作，本文采用離散小波變換方法，經過稀疏化處理得出信號中較大的非零系數，稀疏處理過程描述如下

A=ΩXΩT

(8)

其中，Ω是稀疏基底矩陣；X是原始傳輸數據。稀疏處理后的數據，通過測量矩陣壓縮觀測可表示為

Y=ΨX=ΨΩTAΩ

(9)

其中，Ψ表示測量矩陣；Y表示數據壓縮結果。根據重構恢復算法將稀疏后的傳輸數據進行恢復，并通過逆稀疏化得到原數據。

3 矩陣張量積

壓縮感知技術不僅可以對信息進行壓縮觀測，還能對信息進行加密處理，但加密程度不能抵抗較為嚴重的攻擊。網絡數據傳輸過程中若安全性要求較高，壓縮感知技術無法滿足安全性的需求，因此需要增加信息的加密強度。本文提出矩陣張量壓縮感知方法，不僅可以對不同規模的數據進行觀測，還能大大提高數據的安全性。

張量積是矩陣乘法中一種特殊形式，分為左、右張量積，可實現2個任意大小矩陣間的乘法運算。以右張量積為例，假設矩陣C=[c1，c2，…，cn]和矩陣D的維數分別為m×n和p×q，C?D那么經過計算后的右張量積可表示為

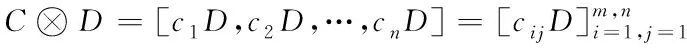
(10)

矩陣張量積運算過程具有矩陣乘法的特性，可以使乘法中的矩陣維數不匹配，即張量積中的左右因式列數與行數不需要相等，這大大提高了矩陣乘法的靈活性。張量壓縮感知模型用公式可表示為

y=E×x

(11)

其中，E表示張量觀測矩陣；x表示被測量的數據信息；y表示觀測值。假定s為左因式列數與右因式行數最小公倍數，進一步將模型表示為

(12)

經過張量積的運算，觀測矩陣的維數變大，從理論上表明觀測矩陣滿足Spark性質、相干性質和有限等距原則。因此可通過矩陣張量壓縮感知對傳輸數據進行壓縮與重構。通過構建，本文設計的新模型可表示為

y=γE×x+ηF

(13)

其中，γ和η表示可變參數，E表示原始矩陣；γ表示輔助矩陣。通過調整γ和η的參數值，可以滿足不同的需求，使加密后的數據信息具有更高的安全性。原始矩陣可以是任意類型的矩陣，當測量矩陣為可逆矩陣時，可完成數據信息的精準構建，這樣可大幅度降低數據節點的存儲。輔助矩陣可以是任意類型的矩陣，通過混沌系統產生的矩陣序列具有良好的統計學特性，且服從均勻分布，安全性較高。

原始矩陣通過Tent混沌系統產生，假定系統參數為λE，初始值為zE0，采樣間隔為dE。通過采樣間隔對數據的采樣，可求出隨機序列，用公式可表示為

(14)

其中，zE(i×dE)表示第i個隨機序列；且滿足g=m/p和h=n/p。按照?Ei=1-2zE(i×dE)對隨機序列進行規格化操作，得到的新序列可表示為

(15)

新序列在區間(-1，1)上均勻分布，通過重新調整結構，可求出原始矩陣E。

輔助矩陣可通過Logistic混沌系統產生，假定系統參數為λF，初始值為zF0，采樣間隔為dF。將系統參數和初值代入混沌系統，并按照采樣間隔進行采樣，可以求出隨機序列，用公式可表示為

(16)

zF(i×dF)是第i個隨機序列。將zF(i×dF)采取規格化處理，得到的新序列如下

(17)

通過重新調整結構，可求出輔助矩陣F。

以往的重構方法通常是把壓縮數據做分割操作，并對分割后的一維信息進行重構，但相鄰的數據信息間具有極強的關聯性，隨著消耗時間的增加，傳統方法嚴重影響了壓縮感知性能，因此采用解凸優化問題的方法，將原始數據的稀疏值用公式表示為

(18)

其中，P表示張量矩陣。該重構算法不僅提高數據重構的效率，還明顯改善了數據重構的效果。

4 傳輸加密算法

在采取對稱加密時，加、解密需要共享密鑰；在采取非對稱加密時，加、解密過程使用不同的密鑰。AES技術廣泛應用在數據傳輸過程中，具體實現過程為：發送方對需要加密的傳輸數據進行加密，通過網絡傳輸將加密后的數據發送給接收方，接收方通過密鑰對密文進行解密，得到明文。加密解密過程如圖2所示。

圖2 AES加密解密過程

發送方與接收方產生的密鑰不能直接傳輸到網絡中，為了提高網絡數據傳輸的安全性，大多情況下密鑰通過非對稱加密方法對密文加密再傳輸，因此密鑰對網絡數據的傳輸安全具有極其重要的作用，一旦密鑰被泄露，攻擊者通過密鑰便可以竊取數據機密，本文采用對稱加密方法對網絡傳輸數據進行加密處理。

AES加密過程是將數據分為多個組，并對每一組進行加密操作，每個組的數據包大小為16個字節，可以選擇不同長度的密鑰，但密鑰長度決定了加密的輪數。AES加密是可逆的，因此AES解密是加密過程的逆過程，通過反序操作即可解密出明文。

數據包屬于TCP/IP協議通信中的數據單元，主要由源IP地址、目的IP地址和網絡負載數據三部分組成，網絡數據傳輸過程需要對數據進行封裝，封裝后的數據包發送過程如圖3所示。

圖3 網絡數據發送過程

用戶數據由數據頭和數據體兩部分構成，但在網絡數據加密傳輸過程中，通常對數據體進行加密，而對包含版本號、數據長度及數據類型等重要信息的數據頭并沒有進行加密。那么攻擊者竊取包含用戶信息的數據頭后，會導致網絡傳輸安全性降低，因此采用TCP協議對數據體和數據頭同時進行加密。

TCP是IP的傳輸層協議，每個TCP只能擁有一個發送端和接收端，當數據傳輸完畢后，需要解釋已經建立好的TCP傳輸連接。由于TCP數據傳輸過程中的數據段大小由應用層的消息大小和最大傳輸單元的大小決定，因此TCP段大小具有不確定性。TCP傳輸通過最大報文段長度判斷是否對數據包進行分段處理。若發送的TCP數據較長，則進行分段處理；若發送的TCP數據較短，等緩存中的數據達到一定長度后再進行發送處理。在采用對數據頭和數據體加密的過程中，若通過密文方式發送數據頭，無法判斷出密文的長度，導致接收端無法確定出密文破解的時間，因此采用固定傳輸大小的方案進行處理。

由AES加密特點，按每組16個字節大小進行分組處理，若數據小于16個字節則對數據填充。TCP傳輸過程如下：將明文大小固定為1kB，若大于1kB則按數據包形式處理；若小于1kB則填充。通過AES對數據頭和數據體進行加密，當接收端收到1kB的數據時進行解密，完成數據的傳輸。

5 仿真與結果分析

為了驗證基于矩陣張量積的輕量網絡數據傳輸加密方法的有效性，在Windows環境中對數據的重構效果與時間消耗兩方面進行測試，其中硬件環境包含接收端、發送端和服務器。在對數據的重構效果分析時，采用峰值信噪比對數據重構效果進行評價，峰值信噪比越大，表明數據的重構效果越好。實驗中采用3組傳輸數據，可變參數γ=0.6、η=0.4，經過實驗，3組數據在不同壓縮比下的峰值信噪比如圖4所示。

從圖中可以看出，隨著壓縮比的增加，3組數據的峰值信噪比均有提升，壓縮比在0.3～0.4之間的峰值信噪比變化率較大，當壓縮比為0.4時，數據的恢復效果依然較好，針對不同數據，隨著壓縮比的增加，數據的峰值信噪比均呈現相同的變化情況，表明本文提出的方法具有較好的數據恢復效果，并且適用性較為廣泛。

圖4 傳輸數據的壓縮比與重構效果圖

為了進一步驗證本文方法的加密傳輸效率，通過統計加密與解密時CPU的計算時間來進行數據傳輸效率的判斷。實驗仍采用3組傳輸數據，將僅加密數據體所需要的時間與本文方法進行對比，通過測試CPU計算時間對加密和解密過程進行分析，結果如表1和表2所示。

表1 加密過程CPU計算時間

表2 解密過程CPU計算時間

從表中可以看出，本文方法雖然同時對數據體與數據頭進行加密，但加密與解密過程CPU計算時間與僅對數據體加密的時間沒有很大差別，并且通過對數據頭的加密，可以使網絡數據在傳輸過程中具有更高的安全性，通過測試，表明本文方法可以滿足網絡數據加密與解密傳輸效率的要求。

6 結束語

為改善壓縮感知模型中測量矩陣和被測量信息列數與行數的匹配度，提高壓縮感知的安全性，提出矩陣張量積感知模型。由于網絡數據傳輸容易遭受到攻擊者對數據信息的竊取，為更好的提高機密效果，采用TPC協議對數據體和數據頭進行加密處理。在Windows環境中，選擇3組傳輸數據，對數據的重構效果與時間消耗兩方面進行測試。實驗結果表明，本文方法壓縮比在0.3～0.4之間的峰值信噪比變化率較大，具有較好的適用性，同時對數據體與數據頭進行加密，CPU計算時間與僅對數據體加密的時間沒有很大差別，說明本文方法完全可以滿足網絡數據加密與解密傳輸效率的要求。