基于閉環模糊控制的擾動觀察法MPPT研究

方勝利，侯貿軍，馬春艷，朱曉亮

(1. 湖北汽車工業學院電氣與信息工程學院，湖北 十堰 442002；2. 十堰巨能電力設計有限公司，湖北 十堰 442000)

1 引言

隨著社會能源問題的不斷凸顯，太陽能作為一種清潔、可再生能源在能源替代和能源升級中扮演著越來越重要的角色。而光伏發電作為太陽能被可靠、廣泛利用的關鍵技術，是近年來能源領域的研究熱點。但由于光伏電池的輸出功率受光照強度、環境溫度等因素影響，且具有典型的非線性特征，因此需采用最大功率點跟蹤算法對其具體實現電路進行控制，以提高太陽能的利用率[1]。而在眾多的MPPT算法中[2，3，4]，由于擾動觀察法具有控制回路簡單、測量參數少、對傳感器精度要求不高、易于實現等優點而被廣泛應用[5]。但該方法也同時存在易于震蕩、部分功率損失、可能誤判等缺點，故需要對該方法進行改進優化。其中文獻[6]提出了先恒壓定位再變步長擾動觀察的方法；文獻[7]提出了根據環境因素實施修正參數變量以尋求最優補償的方法；文獻[8]則提出了一種根據功率變化大小自適應變步長的方法。這些算法均基于具體的數學模型對擾動觀察法進行改進，而由于光伏電池輸出具有時變性和非線性，因此無法同時顧及響應速度和跟蹤精度；文獻[9]、[10]雖然采用了模糊控制算法對步長進行優化，但由于選擇的輸入模糊變量及模糊變量值不合適，且在具體阻抗匹配實現電路上均采用開環控制，導致輸出電壓和功率波動較大，文獻系統響應速度和跟蹤精度都不高；文獻[11]基于神經網絡控制實現最大功率點預測和控制，其跟蹤精度受神經元個數和訓練數據準確度的影響較大；文獻[12]、[13]則分別采用布谷鳥搜索算法和等面積法實現光伏陣列的最大功率跟蹤，但均在系統搜索收斂的情況下可行，約束條件較多。

基于此，本文選擇光伏電池輸出的和作為輸入模糊量，采用模糊控制理論對擾動觀察法進行改進，根據光伏電池的輸出狀態實時調整擾動幅度，提高響應速度、減少震蕩功率損失。此外，為進一步提高系統穩定性和實時性，通過基于PI閉環控制的Boost電路實現系統阻抗匹配。最終通過Matlab的仿真分析進行驗證。

2 光伏電池輸出特性

根據光伏電池的基本工作原理和物理學電子特性，其等效電路模型如圖1[14，15]。

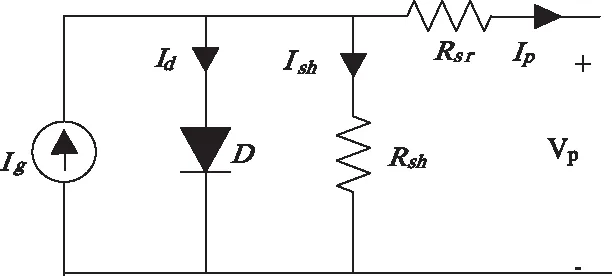
圖1 光伏電池等效電路模型

其特性方程為

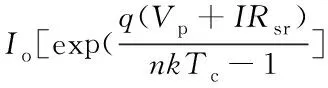
(1)

式(1)中，ISCR為光伏電池在參考光強GR和參考溫度TcR時的短路電流，αT為光電流的溫度系數(硅光電池為0.0017A/K)，G和Tc分別是光伏電池的實際光強和以實際溫度；式(3)中Rsr和Rsh分別是光伏電池等效串聯電阻和并聯電阻；式(4)中n為發射系數(對硅材料典型值為1.3)，k為玻爾茲曼常數，q為電子電荷常數，Io為等效二極管D飽和電流，可表示為

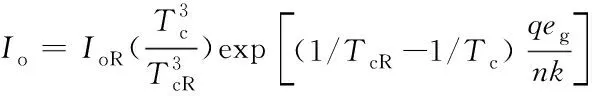
(2)

式(2)中，IoR為參考溫度下的飽和電流，eg為光電材料的帶隙能量常數。

光伏電池輸出功率為

Pp=VpIp

(3)

式(3)中，Pp為光伏電池輸出功率，Vp、Ip分別為光伏電池輸出電壓、電流。

由以上數學表達式可知，光伏電池輸出特性方程為超越方程，其輸出隨著外界光照強度和溫度的變化而變化，且具有典型的非線性特征。

在實際工程應用中，通常對以上標準模型進行簡化得到工程用光伏電池數學模型

(4)

式(4)中，Iscp、Vocp、Imp、Vmp分別為光伏電池在一定光照強度和溫度條件下的短路電流、開路電壓、最大功率點電壓、最大功率點電流，可分別由參考光強和參考溫度條件下的參考值Iscpref、Vocpref、Impref、Vmpref修正獲得

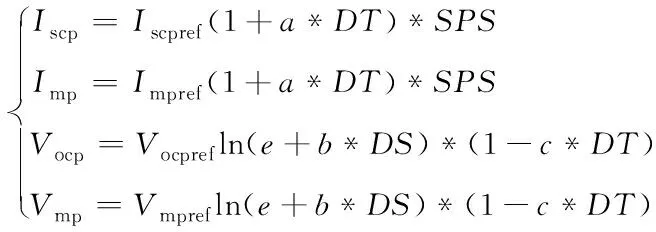
(5)

式(5)中，a、b、c均為補償常數，a=0.0025/℃，b=0.0005/(W/m2)，c=0.00288/℃，且

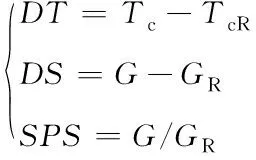
(6)

式(6)中，Tc、TcR、G、GR分別為光伏電池的實際溫度、參考溫度、實際光照強度、參考光照強度。

本文選擇某光伏電池陣列參數為：參考光強GR=1000W/m2，參考溫度TcR=25℃，Vocpref=45V，Iscpref=5.1A，Vmpref=35，Impref=4.5A。在Matlab中建立光伏陣列仿真模型如圖2。

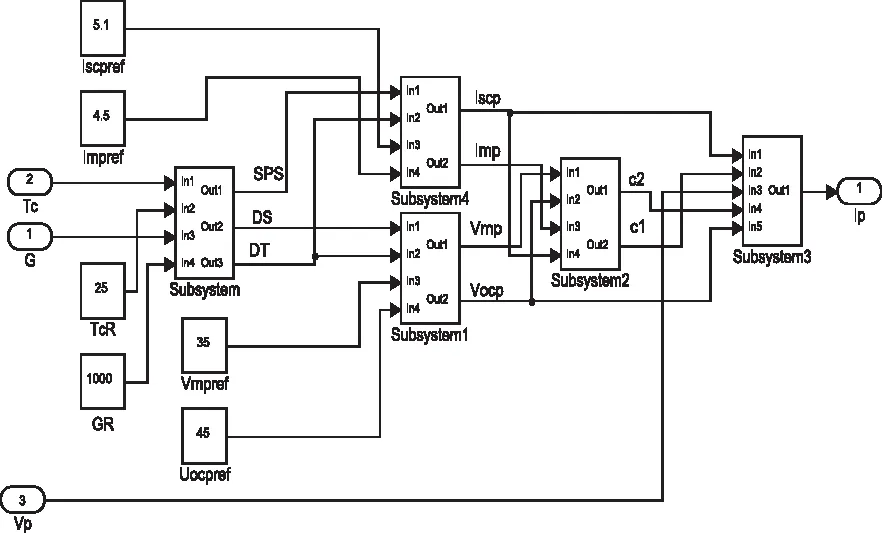
圖2 光伏陣列仿真模型

對圖2所示的光伏整列模型進行封裝，并通過調節其光照強度和溫度，得到當其輸出電壓改變時的輸出特性，該部分仿真模型如圖3，仿真分析如下：

圖3 光伏整列輸出特性仿真模型

1)當溫度恒定(25℃)時，不同光照強度下的輸出特性曲線如圖4。由圖4可知，輸出電流會隨輸出電壓的增大而逐漸減小，而在某一特定電壓下輸出功率達到最大，且其最大輸出功率隨著光照強度的增大而顯著增大。

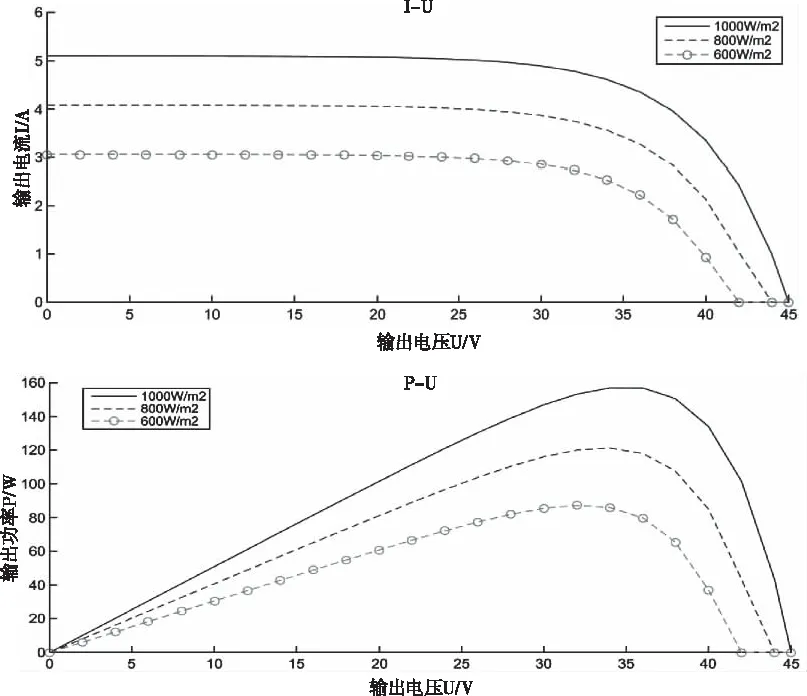
圖4 相同溫度不同光強下的輸出特性曲線

2)當光照強度恒定(1000W/m2)時，不同溫度下的輸出特性曲線如圖5。由圖5可知，輸出電流會隨輸出電壓的增大而逐漸減小，而在某一特定電壓下輸出功率達到最大，且其最大輸出功率隨著光伏電池溫度的增大而略微減小。

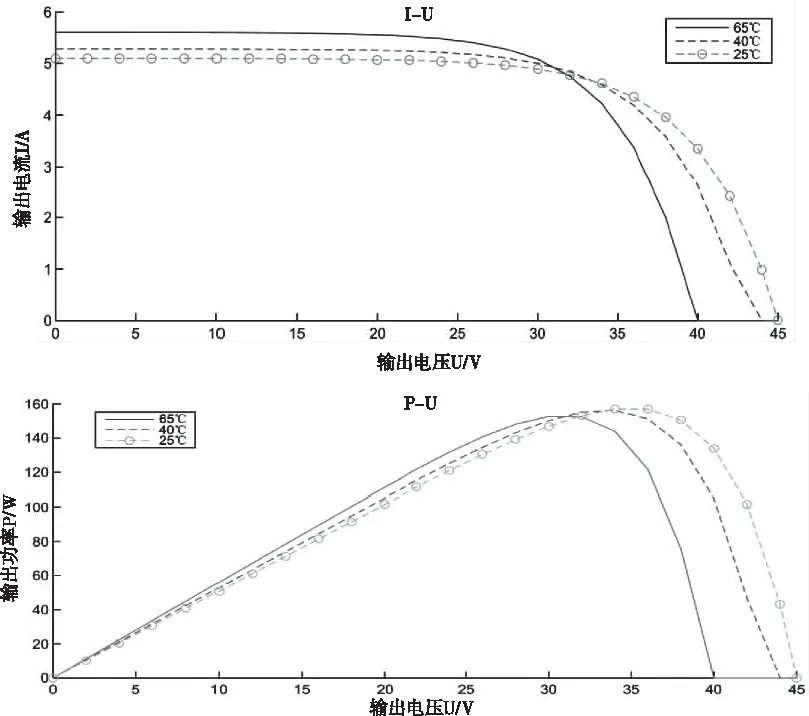
圖5 相同光強不同溫度下的輸出特性曲線

綜合圖4、圖5可知，在一定的外界光強和溫度下，光伏陣列的輸出功率與輸出電壓成“反V字形”變化趨勢，故存在唯一的最大功率點。這為最大功率跟蹤控制提供了理論基礎。

3 擾動觀察法原理

擾動觀察法，作為一種在線式MPPT控制算法，其核心是根據其功率—電壓輸出特性(如圖6)“主動擾動、自動尋優”[16，17]，其基本工作原理是：周期性的改變負載(也即輸出電壓)，并比較負載改變前后的輸出功率大小，從而決定下一步負載的改變方向。若負載改變后輸出功率增大，則下一周期繼續同方向改變負載(如圖中P1點“左側爬坡”)；反之則反方向改變負載(如圖中P2點“右側爬坡”)。如此反復擾動、比較，最終達到最大功率點Pm。

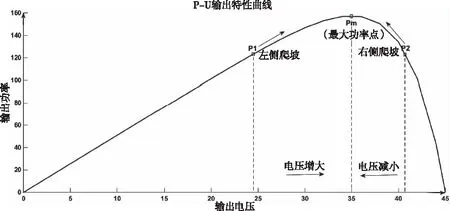
圖6 光伏電池P-U特性曲線

根據擾動觀察法工作原理，其控制流程如圖7所示。

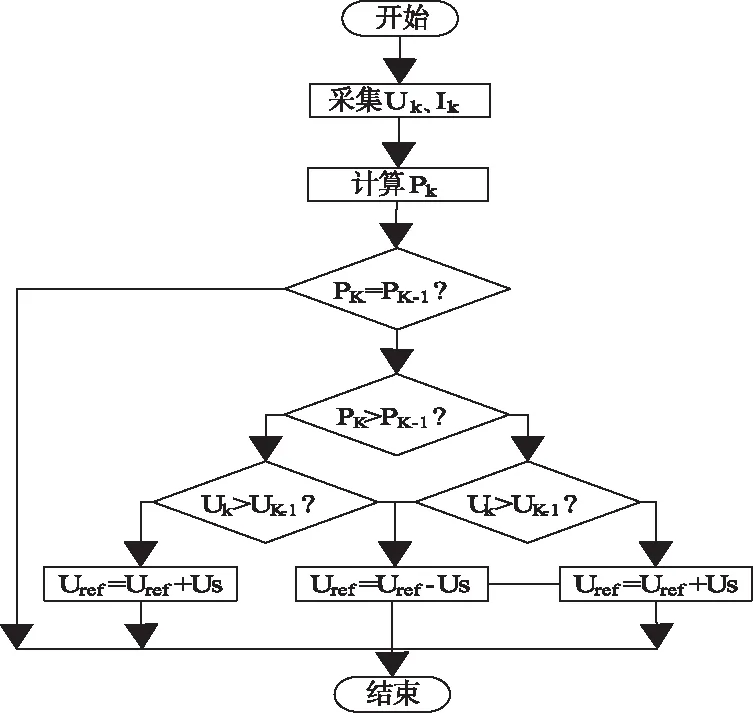
圖7 擾動觀察法控制流程圖

由分析可知，擾動觀察法是通過光伏電池各工作點的輸出功率變化趨勢進行最大功率點跟蹤，故對測量傳感器的精度要求不高，同時還具有算法簡單、需要測量的參數少(僅需輸出電壓和輸出電流)等優點，故易于實現。但當其達到最大功率點時，不會停止擾動，從而在最大功率點附近不停震蕩，造成功率損失，導致其發電效率降低，在環境變化緩慢時尤為突出。當然可通過設置較小的擾動步長來減小震蕩能量損失，但在環境變化較快時，較小的擾動步長會導致跟蹤時間過長，造成大量的跟蹤能量損失[18]。因此設置合適的擾動步長提高光伏發電效率的關鍵。

4 擾動步長的模糊控制

擾動步長的模糊控制即是選擇合適的輸入感應量，并將擾動前后該感應量變化的大小、正負用模糊語言進行描述，并結合光伏電池的輸出特性制定模糊控制規則，經模糊運算和模糊推理后自動調整擾動步長Us，以提高最大功率點跟蹤的速度和精度。

根據上文中對光伏電池P-U輸出特性曲線分析可知，在最大功率點處曲線斜率為零，即dP/dU=0，離最大功率點越近則曲線斜率dP/dU的絕對值越小，離最大功率點越遠則曲線斜率dP/dU的絕對值越大，據此可判斷當前工作點離最大功率點的靠近程度。同時根據dP/dU的正負可判斷當前工作點是在最大功率點的左側還是右側。此外結合電壓變化量dU的正負可判斷當前工作點的運動軌跡。根據這些判斷結果結合實際模糊控制規則來確定適當的擾動步長Us。基于此，本文選擇dP/dU和dU作為其模糊控制器的輸入感應量，并選擇擾動步長Us作為模糊控制器的輸出控制量。其模糊控制結構如圖8。

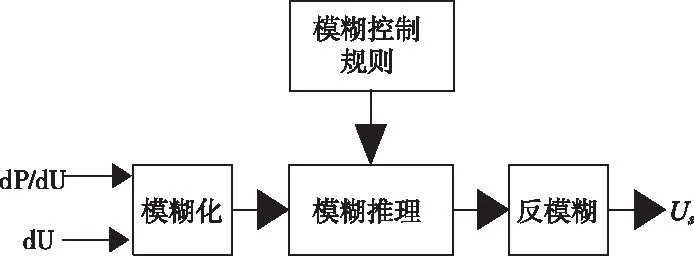
圖8 擾動步長的模糊控制結構圖

為進行模糊運算，首先需要對輸入感應量和輸出控制量進行模糊化。本文選擇模糊量dP/dU和Us有相同的模糊變量值(負大、負中、負小、零，正小、正中、正大)，對應的模糊子集記為

dP/dU，Us={NB，NM，NS，ZO，PB，PM，PS}

其中dP/dU的模糊論域定義為[-5.1，5.1]，模糊子集NB、PB采用梯形型隸屬度函數表示，其它模糊子集采用均勻三角型隸屬度函數表示。其隸屬度函數曲線如圖9。

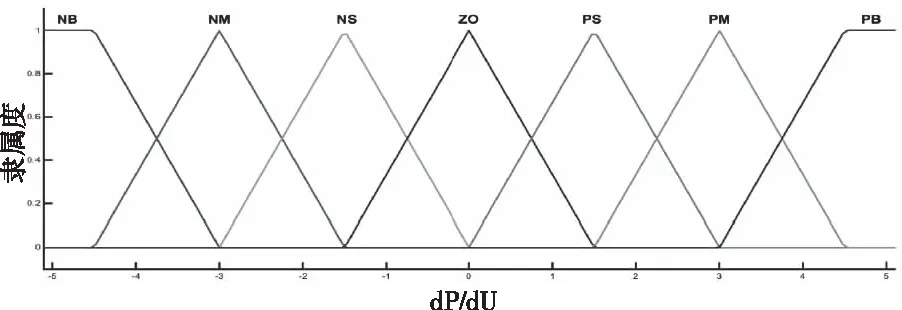
圖9 dP/dU隸屬度函數曲線

Us的模糊論域為[-6，6]，所有模糊子集采用均勻三角型隸屬度函數表示，隸屬度函數曲線如圖10。

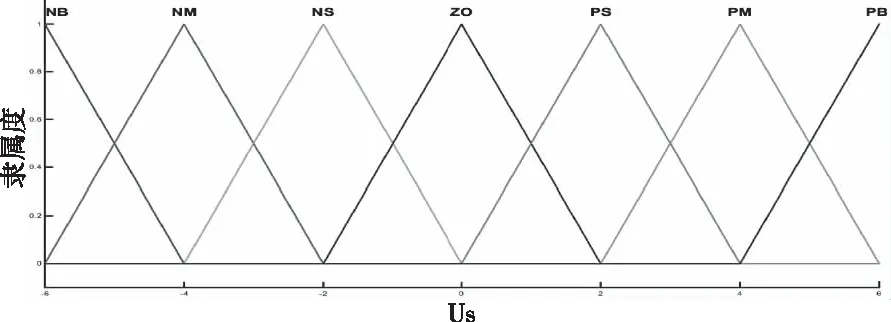
圖10 Us隸屬度函數曲線

對于變量dU，為減少模糊規則數、降低模糊控制調節頻率，選擇dU的模糊變量值為負、零、正，其對應的模糊子集dU={N，ZO，P}。其中模糊子集N、P采用梯形型隸屬度函數，模糊子集ZO采用均勻三角型隸屬度函數，模糊論域定義為[-1，1]。其隸屬度函數曲線如圖11。

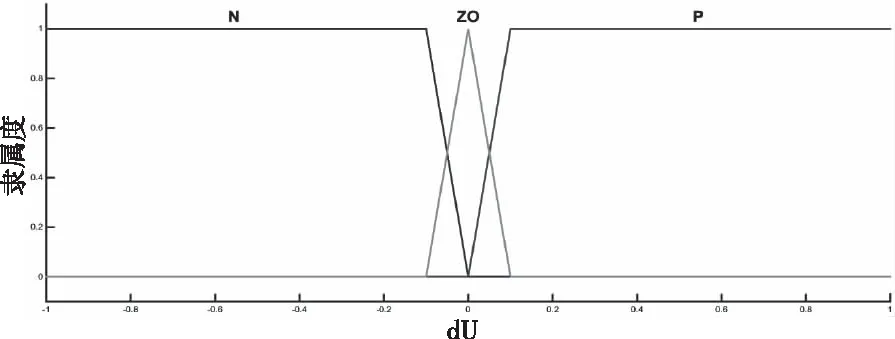
圖11 dU隸屬度函數曲線

對輸入感應量模糊化后需結合光伏電池輸出特性制定模糊控制規則，以便于根據各個工作點處輸入感應量dP/dU、dU的模糊值給出輸出控制量Us的模糊值。為保證光伏輸出具有足夠的跟蹤速度和精度，Us的模糊控制規則見表1。

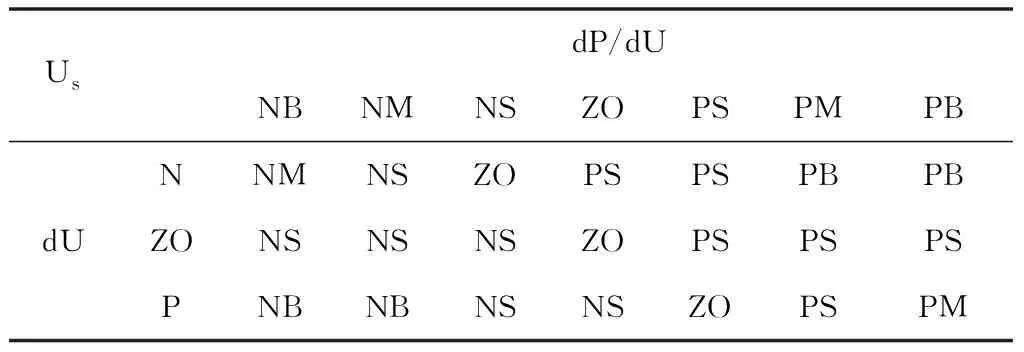
表1 模糊控制規則表

即表示：rule 1：If dP/dU is NB and dU is N，Then Usis NM；

rule 2：If dP/dU is NB and dU is ZO，Then Usis NS；

…

rule 21：If dP/dU is PB and dU is P，Then Usis PM。

本文采用Mamdani法模糊推理，將模糊控制規則表中的第i條規則(rule i，1≤i≤21取整)用等效條件語句代替，即：

rule i：If dP/dU is Aiand dU is Bi，Then Usis Ci

其中Ai、Bi、Ci為分別模糊變量dP/dU、dU、Us的各個模糊變量值。

由此生成第i條模糊蘊涵關系Ri，定義為

Ri(dP/dU，dU，Us)=μAi×Bi×Ci(dP/dU，dU，Us)

=μAi(dP/dU)∧μBi(dU)∧μCi(Us)

(7)

式中：μAi(dP/dU)、μBi(dU)、μCi(Us)分別為模糊子集的隸屬度，符號“∧”表示取小運算。

則由整個模糊控制規則表確定的模糊蘊涵關系為

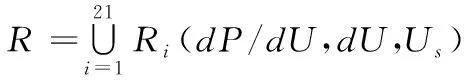
(8)

根據模糊控制器當前實際輸入：dP/dUisA’，dUisB’，可在dP/dU、dU的論域上確定一個模糊集合U，其模糊隸屬度函數可表示為

μU(dP/dU，dU)=μA′(dP/dU)∧μB′(dU)

(9)

則當前輸出Us的模糊集合為

C′=U°R

(10)

式中：符號“°”表示其隸屬度采用上確界算子進行計算。

經過模糊推理得到的僅是輸出控制量Us的模糊值，采用通用的重心法(COA)進行反模糊以得到Us的單一精確值輸出。其算法表達式為

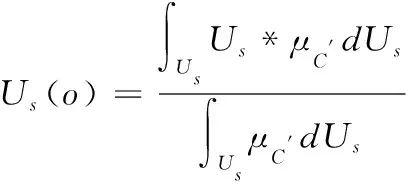
(11)

5 Boost電路閉環PI控制

為具體實現最大功率跟蹤，通常需要引入Boost電路，不僅可實現負載匹配，使光伏電池功率輸出最大，另一方面將光伏電池與后續逆變環節獨立分開，可使發電系統更加可靠。為進一步減小系統波動、消除穩態誤差，提高整體的穩態性能，本文對Boost電路實施閉環PI控制。

系統模糊控制輸出的擾動步長Us(k)也即光伏電池參考輸出電壓Uref與當前輸出電壓U(k)之間的誤差量，通過PI計算對Boost電路中電子開關的調制信號Ur進行控制，然后通過該調制信號Ur和載波型號的比較實現對電子開關的PWM控制，最終使實際光伏輸出電壓能高效跟隨參考電壓的變化而變化，其控制結構如圖12。

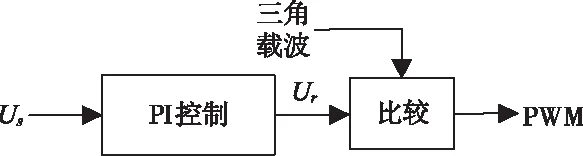
圖12 Boost電路PI閉環控制結構圖

6 Matlab控制系統建模

根據功能分析，光伏發電控制系統結構框圖如圖13。

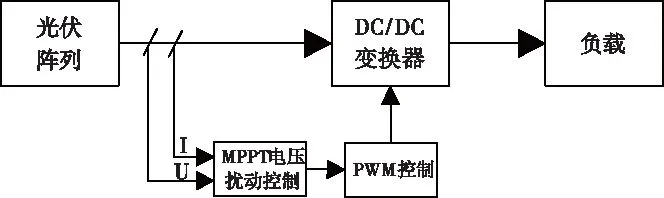
圖13 光伏發電控制系統結構框圖

在圖13中，DC/DC變換器主電路設計參數C1=100μF、C2=300μF、L=10mH，系統負載R=20Ω。對電子開關IGBT驅動脈沖的控制包括兩部分，即基于擾動觀察法MPPT控制模塊和Boost電路PWM控制模塊，在Matlab中建立總體仿真模型如圖14。

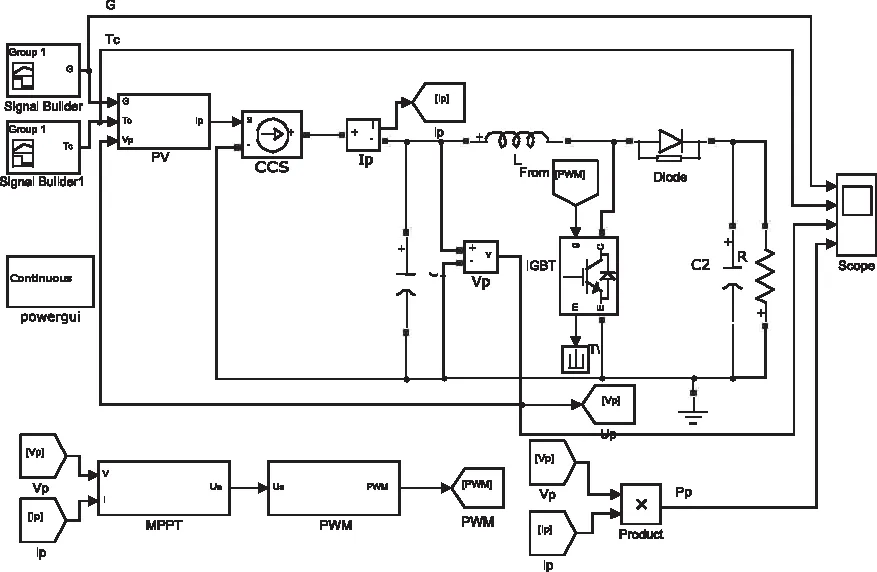
圖14 系統總體仿真模型圖

對圖14中的MPPT和PWM模塊分別采用以下三種方法進行建模分析：

1)建立傳統定步長擾動觀察法MPPT和Boost電路PWM開環控制模型，MPPT模塊和PWM模塊仿真模型如圖15。此時MPPT模塊輸出的Us(擾動步長為定值±0.001)即為Boost電路中電子開關驅動脈沖PWM的調制信號，PWM載波幅值設置為±1。

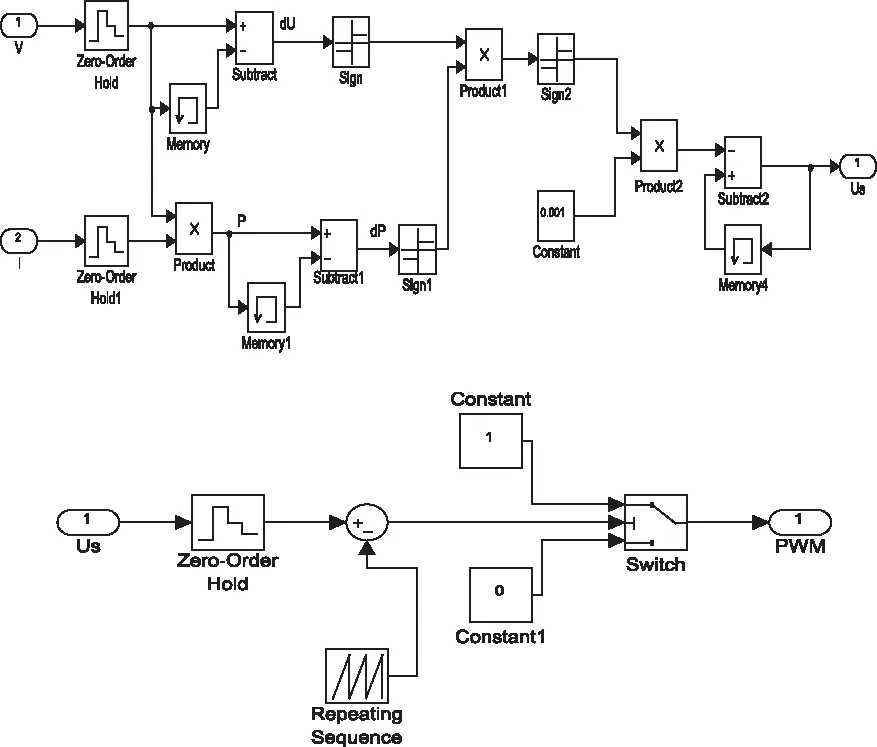
圖15 定步長擾動觀察法開環控制PWM模型

2)建立基于模糊控制的擾動觀察法MPPT和Boost電路PWM開環控制模型，MPPT模塊和PWM模塊仿真模型如圖16。此時MPPT模塊輸出的Us(變步長)即為Boost電路中電子開關驅動脈沖PWM的調制信號，PWM載波幅值設置為±10。

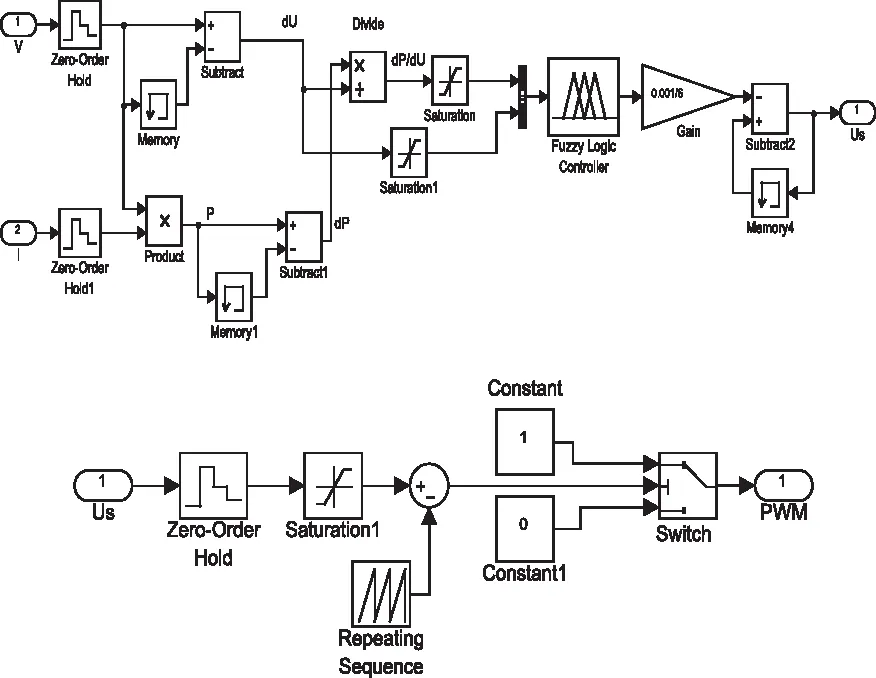
圖16 改進型擾動觀察法開環控制PWM模型

3)建立建立基于模糊控制的擾動觀察法MPPT和Boost電路PWM閉環PI控制模型，MPPT模塊和PWM模塊仿真模型如圖17所示。此時MPPT模塊輸出Us為擾動電壓，其經PID控制輸出Boost電路中電子開關驅動脈沖PWM的調制信號，PWM載波幅值設置為±10。

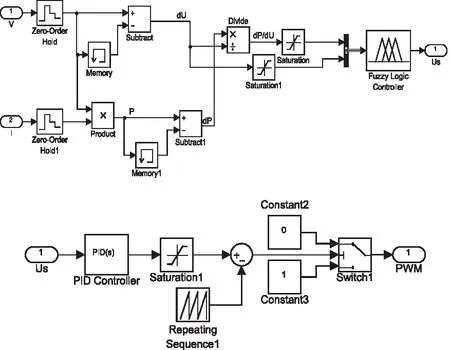
圖17 改進型擾動觀察法閉環控制PWM模型

7 仿真及分析

在Matlab環境中采用ode45變步長仿真算法對以上模型進行仿真，為檢驗當光照強度G和溫度Tc變化時光伏陣列的功率跟蹤效果，本系統按照表2在特定時刻改變光伏陣列光照強度G或溫度Tc條件，并經式(3)～(6)計算出其在設定條件下理論最大功率點電壓Vp及最大功率Pp。

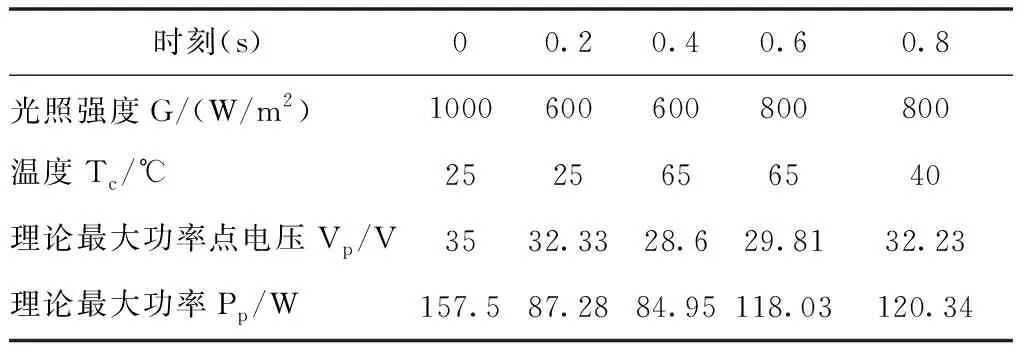
表2 環境條件變化

圖18、圖19分別為采用傳統定步長擾動觀察法MPPT和Boost開環控制(控制方法1)、基于模糊控制的改進型擾動觀察法MPPT和Boost開環控制(控制方法2)、基于模糊控制的改進型擾動觀察法MPPT和Boost閉環PI控制(控制方法3)等三種控制方法在設定條件下的光伏陣列輸出電壓(Vp1、Vp2、Vp3)和輸出功率(Pp1、Pp2、Pp3)的變化曲線。

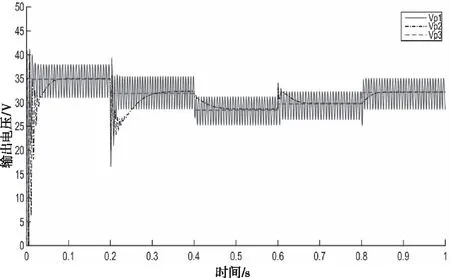
圖18 光伏陣列輸出電壓變化曲線

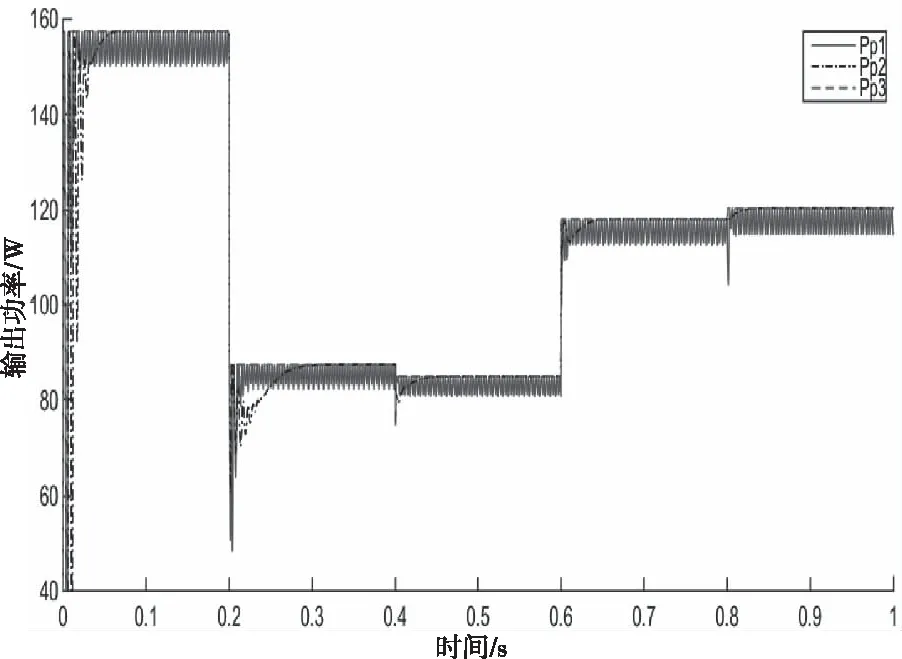
圖19 光伏陣列輸出功率變化曲線

對圖18、19進行分析，其仿真結果見表3。

表3 仿真結果

對表3中的數據進行分析比較可知，采用本文設計的基于模糊控制的改進型擾動觀察法不僅可使光伏陣列輸出達到且近似穩定在最大功率處，獲得較高的最大功率跟蹤精度，而且采用PI閉環控制的Boost電路可使系統能高效跟蹤外界光照強度和環境變化時的最大功率點，獲得較快的最大功率跟蹤速度，兩方面結合，從而極大的提高光伏電池的發電效率。

8 結束語

本文在對光伏電池輸出特性進行分析的基礎上，將模糊控制算法引入擾動觀察法最大功率跟蹤中，并對其Boost實現電路進行PI閉環控制。通過Matlab仿真分析和對比，驗證了該控制算法能兼顧光伏電池最大功率跟蹤的實時性和穩定性，在提高其跟蹤精度的同時可提高其跟蹤速度，為改善光伏發電性能、提高光伏發電效率提供了一種重要的控制方法。