基于多元線性回歸的新車型投產時間預測研究

徐雯霞 黃世杰

(同濟大學，上海 201804)

0 引言

汽車產品的銷量逐年遞增，隨之而來的產品質量投訴也日益增多。由2021年車質網的統計報告可知，汽車的投訴量在2010—2020年間增長了近50倍，其中有約40%的投訴內容來自整車產品質量問題。這既反映了國內消費者對汽車產品的質量要求和期望在不斷提高，也說明了為了加快新車型的上市速度，大部分車企很有可能在產品設計或生產工藝上沒有做好充分驗證。

投產又稱為新項目導入，即企業把概念化和數字化的設計轉化為規模化量產的消費產品，主要任務是按時實現質量達標的整車產品以及配套達標(設計產能、穩定性)的生產線的量產，并實現高效率生產的經濟效益。投產環節緊密銜接設計—制造—質量，可有效驗證產品設計缺陷、防堵制造工藝漏洞、試錯作業員可能存在的操作失誤，使生產線上的新工藝和新員工順利完成磨合和爬坡，使整個產品線高效穩定運行。這是汽車產品成功投放市場、維護品牌良好口碑必不可少的環節。

1 新車型投產時間的影響因素

目前，各大合資車企對投產時間的預測仍以經驗總結和專家評審的方式為主，雖然欠缺科學性的論證，但仍然具有較高的參考價值。很多車企在制訂新車型投產計劃時會進行專家評審，并充分結合之前新項目投產時積累的經驗，盡量避免以過多的假設承擔計劃外的風險[1]。分解并羅列投產階段的關鍵路徑以及影響其所需要的時間的行為，即可得出影響投產時間的關鍵因素。PT1和PT2的持續時間和需要驗證的工藝站點數量和復雜程度相關，所以“新工藝設備驗證”也是投產時間影響因素之一。對各類型合資車企影響投產時間的因素進行總結，見表1。

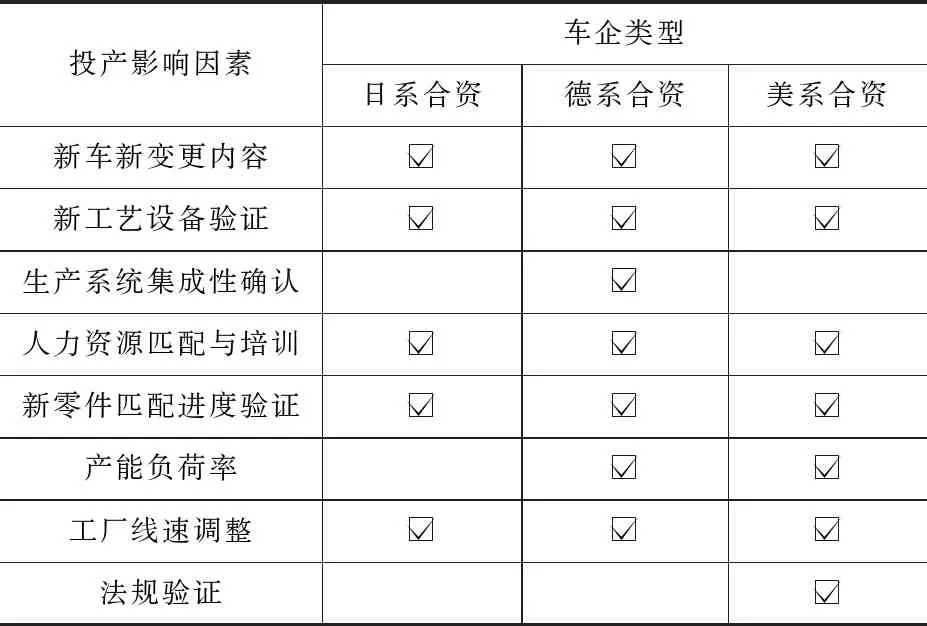
表1 影響投產時間的因素

2 新車型投產時間預測模型構建

通過對投產階段關鍵步驟的調研與歸納，結合福特汽車的投產管理模型(LQOS)，構建新車型投產時間影響因素的數據庫：上車身變化為X1，下車身變化為X2，動力總成變化為X3，工廠線速或生產節拍為X4，工廠班次為X5，新車型投放市場的數量為X6，工廠在產車型的數量為X7；因變量Y為投產所需的時間(以周為單位)[2]。將過去5年間投產的新車型的投產數據作為模型樣本，新車型投產時間統計見表2。

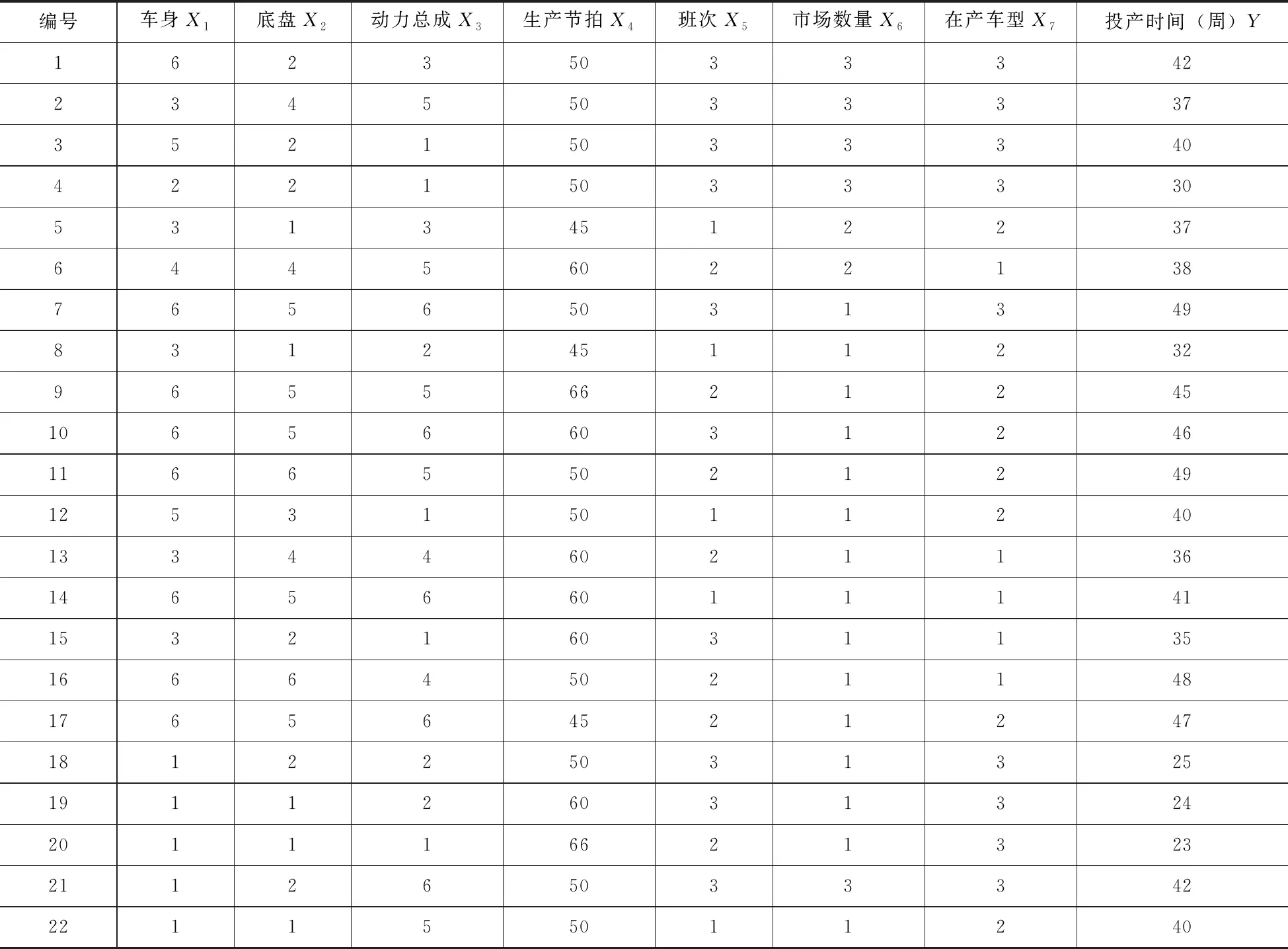
表2 新車型投產時間統計

其回歸模型為：Y=β0+β1X1+…+β7X7+ε。其中，βn是未知參數，稱為回歸系數；ε是均值為0、方差為σ2(σ>0)的隨機誤差，代表其他隨機因素對投產事件Y產生的影響。對于總體(X1，X2，…，X7；Y)的n組觀測值(x11，x22，…，x77；yi)(i=1，2，…，7)，線性回歸模型可用矩陣表示為：Y=Xβ+ε。

利用SPSS軟件計算多元線性回歸模型，對線性回歸方程進行求解，如下

REGRESSION

/MISSING LISTWISE

/STATISTICS COEFF OUTS R ANOVA

/CRITERIA=PIN(.05) POUT(.10)

/NOORIGIN

/DEPENDENT投產時間

/METHOD=ENTER車身 底盤 動力總成 節拍 班次 市場數量 在產車型

/SCATTERPLOT=(*ZPRED，*ZRESID)

由SPSS的計算結果分析：

(1)調整后R方為0.73，也就是說明在所選自變量中能夠解釋因變量投產時間變化的73%，也就是說投產時間的變化情況中有73%是由于以上變量影響造成的。在統計學中只要變量影響達到30%就代表關系成立，所以所選參數設置是可以被接受的。

(2)德賓-沃森值為1.679，接近2，說明方程各自變量之前自相關性可以被接受，但數值與標準值仍有所偏差，暫時猜測為某一個或者幾個變量可能存在一定的自相關性或者共線性。

(3)方差分析結果(ANOVA)，模型的P值(顯著性)為0.00，遠小于0.05，證明模型至少含有一個自變量對因變量Y(投產時間)存在顯著影響，所以此模型顯著性關系成立。

由此得出以下回歸方程，用于表示因變量投產時間與自變量影響因素之間的關系

y=2.548x1-0.981x2+1.997x3-0.078x4+2.881x5+0.047x6+0.111x7+17.763

方程系數的解集見表3。

各個數據的VIF值除了“下車身變化”，其余自變量的VIF值均小于5，見表3(嚴格的統計學意義中，VIF小于5說明變量之間沒有強烈的共線性)，說明除了“下車身變化”可能與其他變量存在共線性，其余變量均為相互獨立的自變量。表3中上車身與動力總成變化的顯著性分別為0.002和0.004，遠小于0.05，說明上車身變化量能夠顯著影響投產時間的長短，同時系數分別為B1=2.548、B3=1.997。也就是說，上車身和動力總成的變化范圍與投產時間成正比，符合模型之前的原假設，這兩個變量X1和X3對于方程成立。

表3 方程系數的解集

另一個變量X5班次的顯著性參數為0.061，也非常貼近0.05。考慮到樣本數量存在不夠充分的潛在缺陷，暫時認為此變量也對因變量Y投產時間有顯著影響。系數B5=2.811，為正值，也與模型原假設一致，故也可認為其成立。

自變量下車身變化X2和生產節拍X4對于方程不成立，因為這兩個自變量的系數計算結果為負數，與原假設和實際情況不符，即下車身變化范圍和工廠節拍越大，投產所需的時間越長。同時，下車身變化也不滿足統計學共線性(VIF<5)的指標。

3 殘差分布分析

標準化殘差的直方圖如圖1所示，顯示殘差值分布集中于-1.5～1.5，不吻合正態分布，因此按照這些樣本分析出的模型并不能很好地匹配自變量和因變量的關系，此線性回歸模型存在問題，有可能是問題變量所造成的，即“下車身變化”和“工廠線速或生產節拍”。

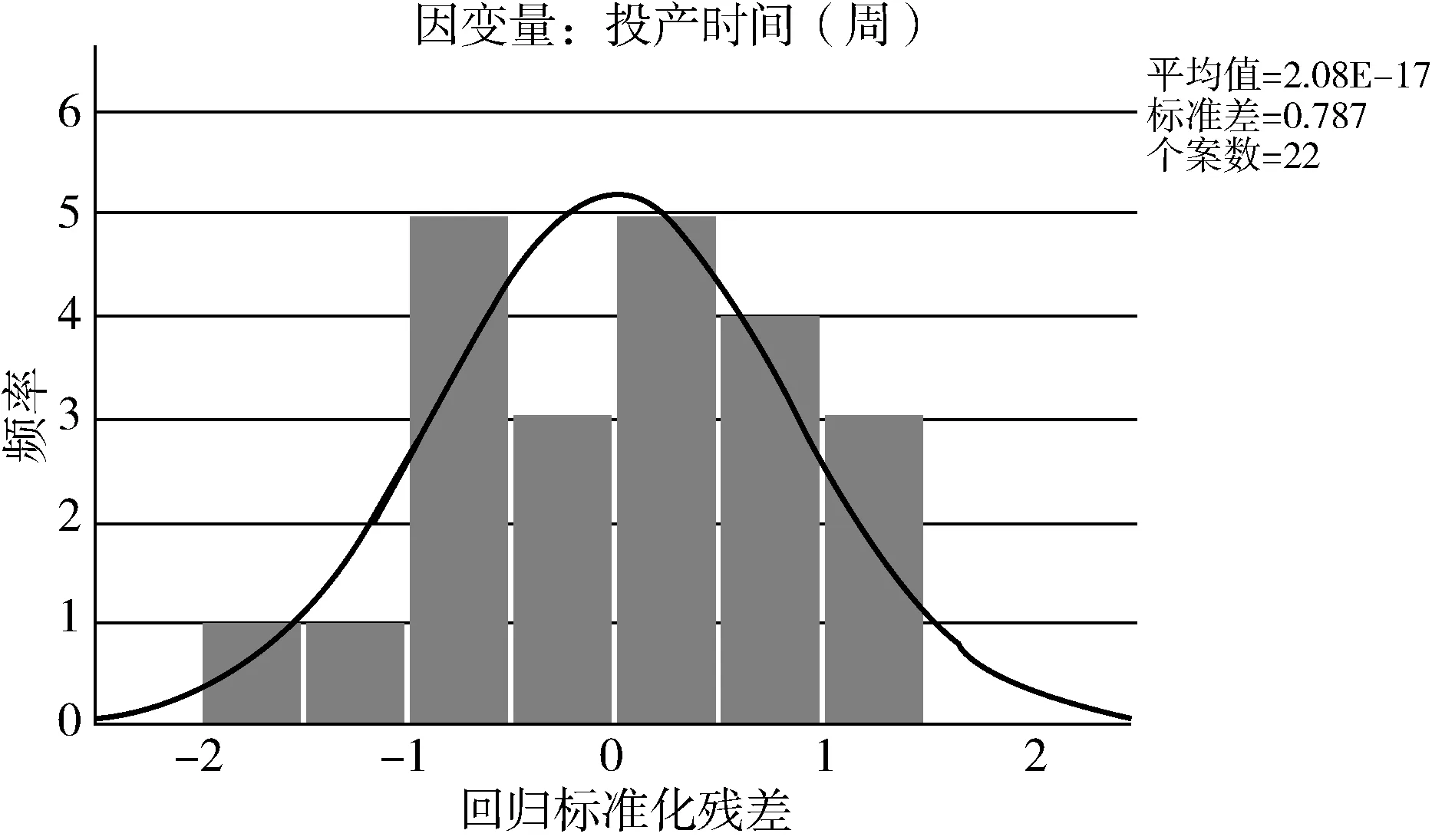
圖1 標準化殘差直方圖

4 預測模型的修正

刪除問題變量進行變量調整[3]，重新利用SPSS計算。調整后模型R方為818，相較調整前R方835并沒有因為變量的減少而降低，反而增大了，有可能是因為去除了干擾的無效變量反而使得模型更能契合自變量對因變量造成的影響。同時，德賓沃森指數由1.697增大為1.841，調整后的模型比原模型更接近2，說明新的模型比原模型的自相關性更低，優于原假設。

調整后的模型顯著性為0.000，小于原模型的0.001，遠小于0.005，說明顯著性上更新的模型也要優于原模型。

修改后的模型VIF值均小于5且遠小于原模型，因此說明各個變量基本不存在共線性，更新后的模型和自變量切合度更高，同時變量對應的系數均為正值，這也符合原假設即這些自變量均與因變量成正相關性。

相較于原回歸模型的直方圖，修正后的模型殘差更貼近于正態分布，如圖2所示。表示模型預測出現誤差的概率更趨于隨機性或者意外性，從而證明利用修正后的模型具有更高的概率預測出實際的自變量和應變量的變化關系，模型的殘差正太分布可以被接受[4]。線性回歸方程按照修正后的模型系數解得

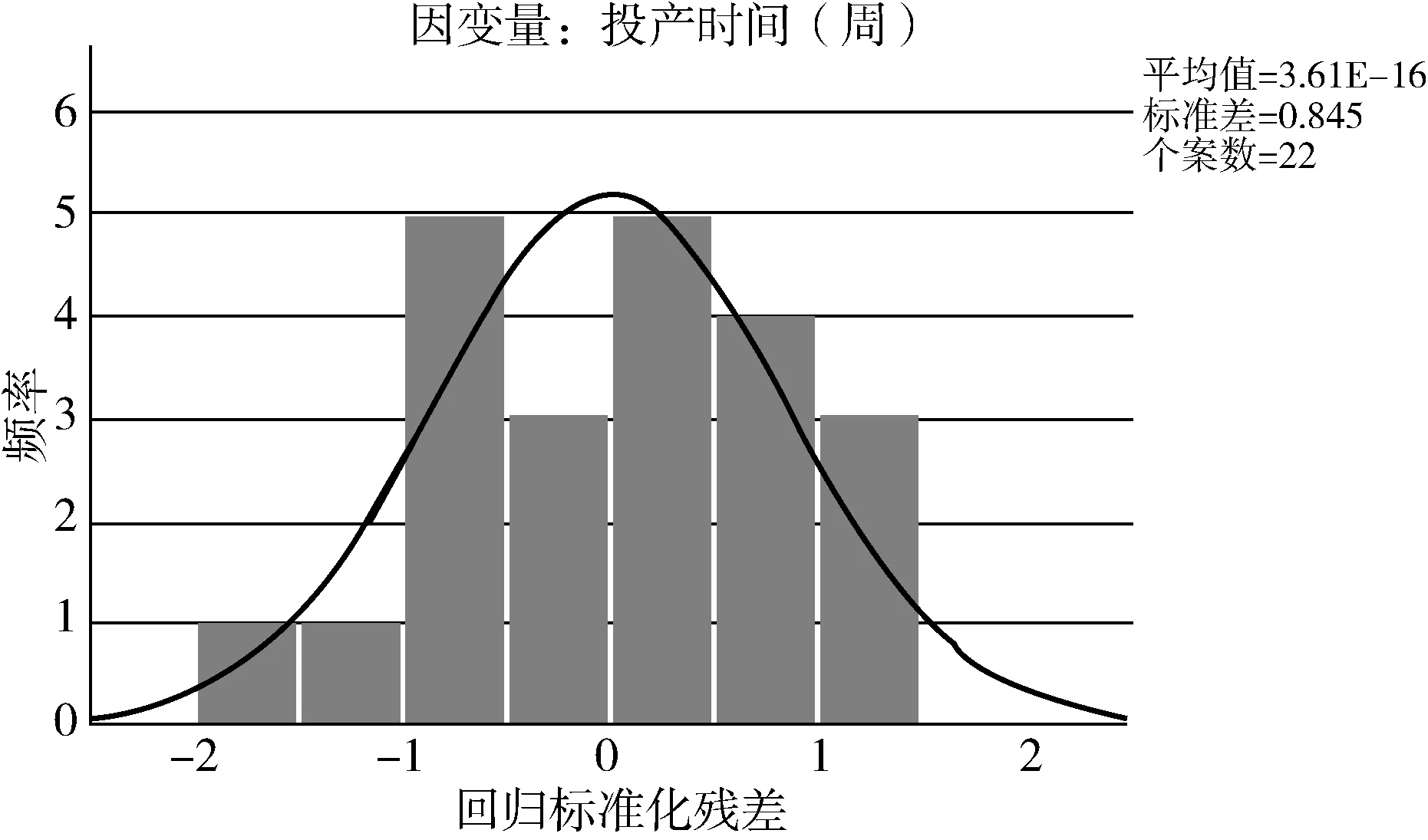
圖2 調整后模型殘差直方圖

y=2.804x1+1.619x2+1.927x3+0.635x4+0.79x5+14.082

5 誤差變量分析

在實際案例中，下車身的變化往往不會單獨發生，而是與上車身變化或者動力總成變化同時發生，或者說它必然會和其他兩個變量中的一個或者兩個同時存在強相關性。因為從新車型設計的角度而言，下車身的變化一般都是被動調整以滿足上車身的變化需求，如車型的換代升級增加了科技配置使底盤的布線布置和前后橋設計需要調整，又或者為了滿足燃油經濟性對原有發動機進行換代升級而對底盤進行設計變更用以匹配調教全新的動力總成配置等。不管是哪種情況，基本不會單獨對下車身單獨做設計變更，并且大部分整車廠會選擇盡量不更改底盤設計。所以，實際上沒有下車身變化獨立產生的情況，也不會對投產時間造成真正的顯著影響。

另一個問題變量是生產線節拍，節拍越高，則制造相同數量樣件時所需的時間越少。雖然理論上這樣的邏輯是成立的，但在工廠實際運營中有另外一個關鍵參數，即“產能利用率”。工廠生產線節拍提升的主要原因是產量的需求增加，節拍高的產線相比節拍低的產線每日的產量更大，根據“交付客戶優先”的管理原則，大部分車企會優先實現量產交付，這也意味著可以被投產樣車試制所利用的富余產能其實比低線速的工廠更少。與此同時，由于線速的加快對于操作工和一線管理的難度加大，需要更長的時間將產能爬坡至量產需求的穩定性(一般OEE85%以上、FTT90%以上)，生產節拍在某些情況下與投產時間成正比關系。據此，該假設與原模型中成反比(系數為-0.78)不匹配。

6 結語

基于影響投產時間的關鍵因素建立數據庫，采用多元線性回歸模型并利用SPSS軟件對投產時間影響因素進行多元線性回歸分析。在得出方程系數的初步計算結果后對回歸方程進行R方、顯著性、變量共線性和殘差分的檢驗，發現兩個共線性較強的干擾變量。對變量進行刪選并重新建模，得出的新方程解在自相關性和系數顯著性上明顯優于原方程，且更貼合正態分布的曲線。雖然可能由于樣本數量不夠的關系，依然存在少數變量的顯著性不夠，但是從統計學的角度，優化后的方程符合應用標準，故優化后的模型理論上可以成立。同時，結合實際的投產管理和生產制造經驗對篩選出的干擾變量進行分析，解釋其在現實案例里的實際意義。各個系數和解均滿足多元線性回歸方程的擬合度要求，并且大部分可以與實際案例相聯系。為了使模型回歸更準確，還需要進一步擴大樣本搜集數量，并結合新智能制造的技術方案不斷優化模型參數。